激光测量机器人手眼标定共轭对建立方法

郑凯， 金路， 梁金华

(上海航天精密机械研究所，上海 201600)

激光测量机器人手眼标定共轭对建立方法

郑凯， 金路， 梁金华

(上海航天精密机械研究所，上海 201600)

提高测量机器人系统的手眼标定精度是激光测量机器人推广应用的关键问题，提出了一种测量机器人手眼标定共轭对建立的方法，通过半径已知的精密靶球标定激光器坐标系与工业机器人末端法兰坐标系间的相对变换矩阵，建立机器人位置姿态信息和靶球球心坐标组成的共轭对。

激光测量机器人; 手眼标定; 共轭对

0 引言

航天零部件中有较多的复杂外形曲面零件，这类零件在工程实际中的作用越来越显著。由于这些零件的加工过程复杂，加工成本高，所以对其误差的检测过程有着更高的要求，但传统的测量方法要么效率太低，要么无法达到精度要求。本文涉及的激光测量机器人就是针对复杂曲面的测量而开发的系统，它由工业机器人搭载成品化的激光器组成。其中激光器输出的数据是光平面上的被测物体的二维数据，激光器有厂家内置的坐标系。激光器固定到工业机器人末端手臂上之后，不考虑环境因素影响的话，激光器坐标系与工业机器人末端法兰坐标系的相对变换矩阵就唯一确定，且激光器拆卸再安装前不会改变,这个坐标是整个测量坐标系转换必不可少的一个环节。

手眼标定，即激光器坐标系与工业机器人末端法兰坐标系的相对变换矩阵的确定，往往通过一个半径已知的高精度靶球(圆度要求不大于0.001mm)，理想情况下机器人以不同的位置姿态使激光器恰好输出靶球球心所在的最大圆弧，通过圆拟合可求出最大圆弧的圆心即球心，此时机器人位置姿态信息与靶球球心坐标即组成一个共轭对，然后建立多个共轭对，并以球心相对于机器人基坐标系位置不变作为约束，即可求解激光器坐标系与工业机器人末端法兰坐标系相对变换矩阵,在国内外的文献中均有对此方法的应用研究和效果描述[1-3]。

而实际标定中很难人为控制机器人使激光器恰好能输出靶球球心所在的最大圆弧，目前国内外最常用的做法是输出靶球某一圆弧，该圆弧半径与靶球半径、该圆弧圆心与靶球球心距离构成直角三角形，通过计算该圆弧圆心与靶球球心距离得到靶球球心的坐标。由此可见，该方法没有准确建立机器人位置姿态信息与靶球球心坐标的对应关系，现有方法建立的对应关系并不是机器人位置姿态信息与靶球球心坐标对应关系的真实反映[4]。

1 共轭对建立方法

为改进现有方法的不足，准确建立机器人真实位置姿态与靶球球心坐标的对应关系，本文提出一种基于优化方法的搜索过程，控制机器人运动使激光器恰好输出靶球球心所在的最大圆弧。首先本文提供了一种准确建立共轭对，即机器人位置姿态信息与靶球球心坐标的对应关系的方法，其特征在于：将每一次建立 共轭对的过程视为一次优化，以六自由度工业机器人各关节轴码盘数为优化变量，以工业机器人系统基坐标系某一坐标轴方向为搜索方向，以激光器输出靶球球心所在的最大圆弧为优化目标展开搜索，从而不断控制工业机器人进行位置和姿态调整，直至满足迭代终止条件。具体步骤如下：

(1)人工通过示教盒手动控制机器人运动，使激光器的光线投射到靶球表面，由于靶球在机器人工作范围内可以任意放置，这一步骤主要目的是由人工引导机器人至靶球；

(2)系统开始自动化过程，首先接受激光器输出光线投射位置处的圆弧离散点数据，通过圆拟合计算初始位置下的圆弧半径，然后在机器人基坐标系下，由标定程序分别控制机器人沿X、Y和Z坐标轴方向平移一个微小步长，激光器分别输出圆弧离散点数据，程序计算出对应圆弧的半径大小，与初始半径相比，选择半径变化最大的坐标轴方向作为本次搜索方向；

(3)选定本次搜索方向后，通过外推法确定圆弧半径的“小-大-小”搜索区间，由此球心所在的圆弧必在搜索区间两端“小”圆弧半径所在的位置之间；

(4)按照区间消去原理不断减小搜索区间，直至计算得到的圆弧半径与已知靶球半径差值的相对值满足迭代条件，此时六自由度工业机器人各关节轴的码盘数，以及激光器坐标系下计算出的圆弧圆心坐标，形成一个共轭对；

(5)在工业机器人形成前一个共轭对的最终姿态的基础上，按照标定程序的设定，自动控制机器人至下一个姿态，重复(2)-(4)的过程，形成后续所需要的多个共轭对；

(6)在已有的多个共轭对的基础上，后台就可以计算激光器坐标系与工业机器人末端法兰坐标系相对变换矩阵，即完成手眼标定，如图1所示。

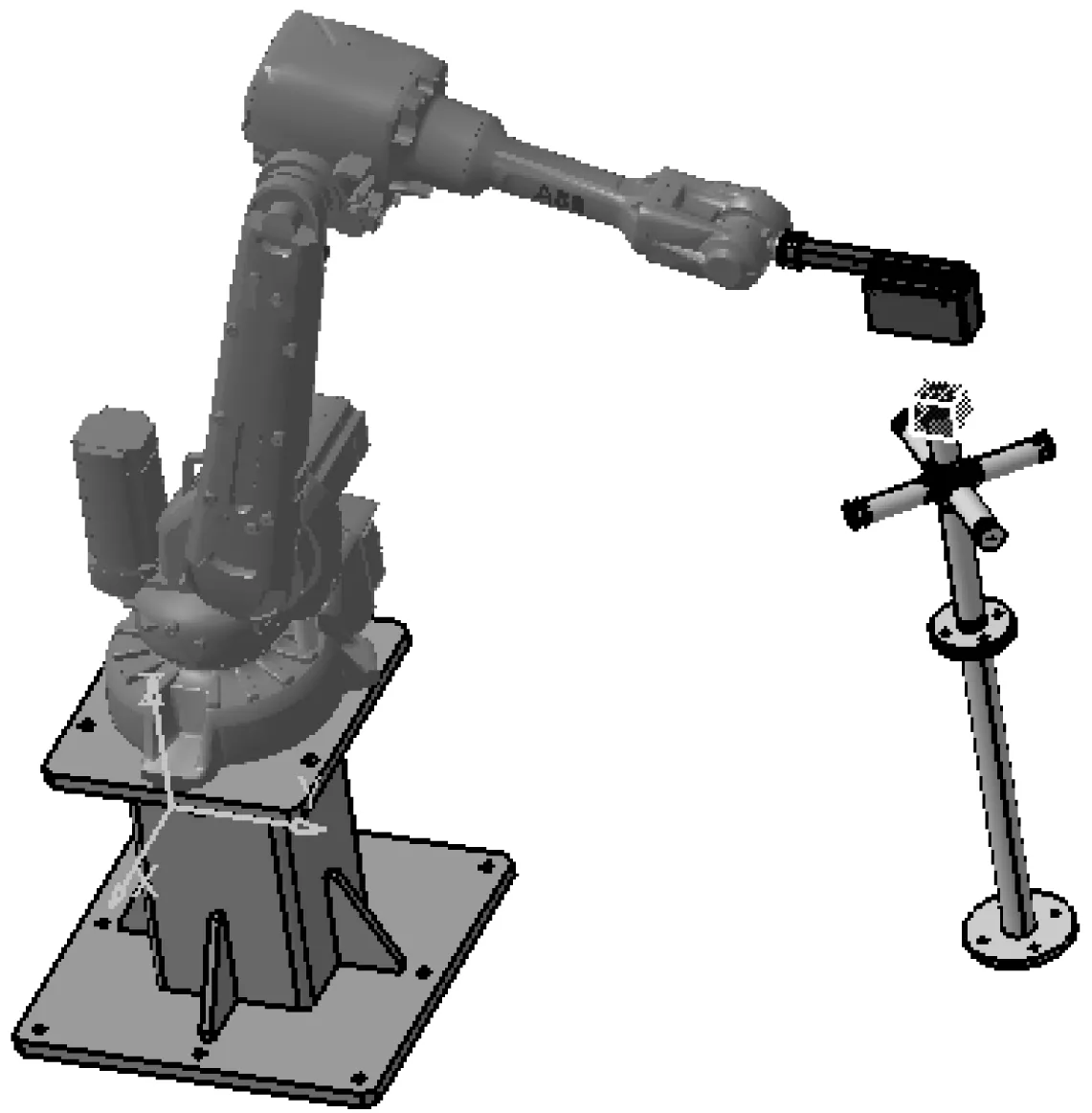
图1 激光测量机器人与标定靶球

通过借鉴优化设计的思想，将每一个共轭对的形成视为一个优化过程。首先，由于标定参照物是一个半径已知的精密靶球，所以球心唯一确定，且过球心有无穷多个切圆，且有无穷多个方向，即必存在无穷多个共轭对，且形成每一个共轭对的过程中必有最优解；其次，搜索方向通过简单寻优确定，即由工业机器人分别沿基坐标系的3个坐标轴方向平移微小步长，激光器分别输出圆弧离散点，并计算圆弧半径，以半径变化最明显的方向作为搜索方向，可以保证最优解的存在；搜索方向确定后，优化过程仅仅是一个简单一维搜索的过程，如果初始位置要求激光器的光线投射到最大圆弧附近，计算将变得更加简单，收敛速度将更快。

2 共轭对标定试验

下面对激光测量机器人手眼标定共轭对建立方法的具体试验过程结合附图进行详细说明。

(1)通过示教盒手动控制机器人运动，目测使激光器发出的光线大致投射到靶球表面的最大圆弧位置，从理论上说使激光器的光线投射到靶球表面任意位置都可以，但为了缩短优化过程，提高收敛速度，要求简单目测使激光器的光线投射到最大圆弧附近；

(2)在软件中启动手眼标定程序，程序首先接收初始位置下激光器光线投射位置处的圆弧离散点数据，并通过圆拟合计算出圆弧半径，然后控制机器人在基坐标系下，分别沿X、Y和Z坐标轴方向平移一个微小步长，激光器分别输出圆弧离散点数据，并且程序计算出对应圆弧的半径大小，与初始半径相比，选择半径变化最大的坐标轴方向作为本次搜索方向；

(3)选定本次搜索方向后，以圆弧半径为目标，通过外推法确定“小-大-小”搜索区间，即第一个位置下激光器输出的圆弧半径r1，第二个位置下圆弧半径r2，第三个位置下圆弧半径r3，有以下关系r1r3，由此球心所在的圆弧必在r1所在位置和r3所在位置之间，搜索过程示意图，如图2所示。

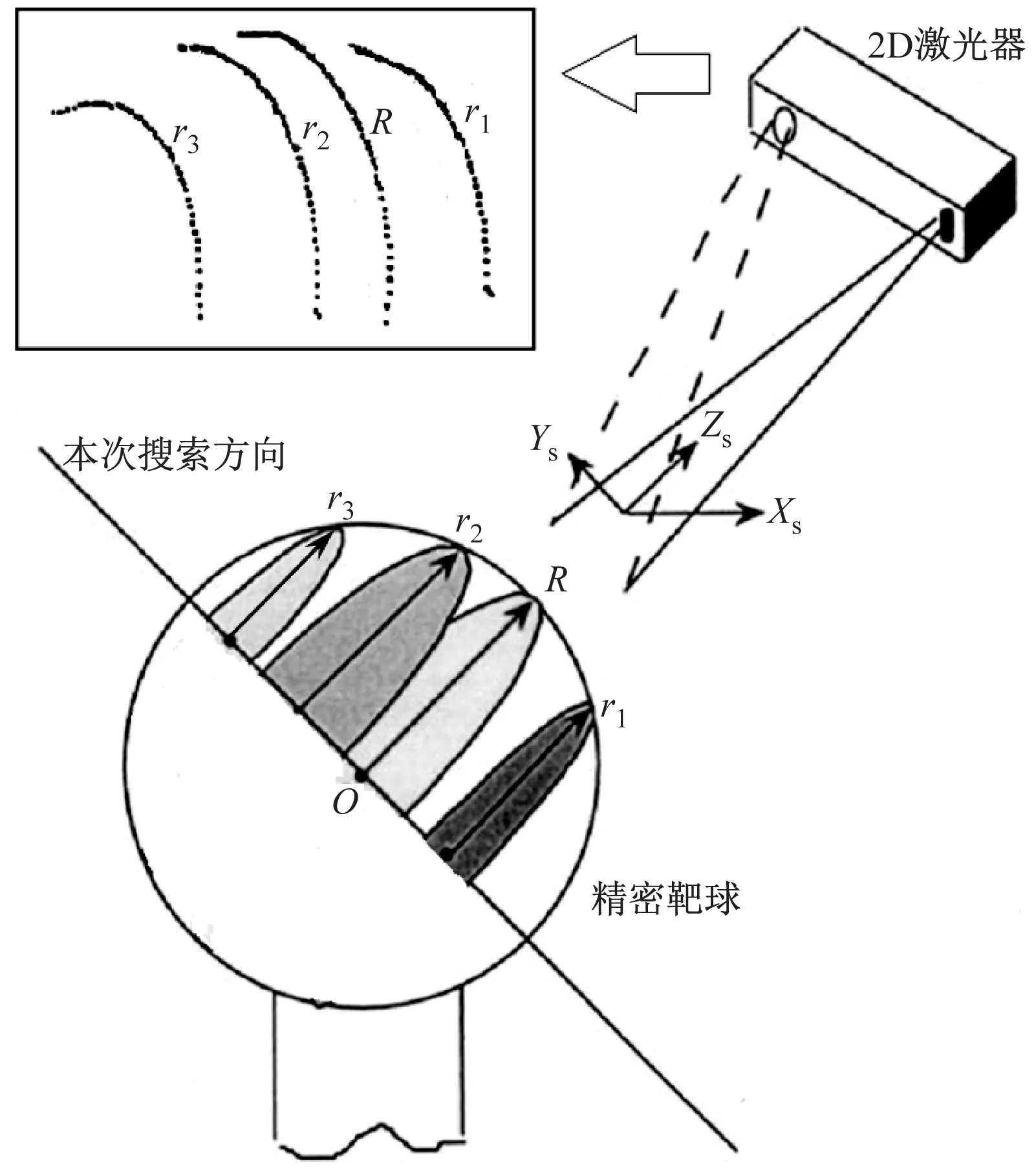
图2 自动寻优建立共轭对的过程示意图

(4)按照区间消去原理不断减小搜索区间，直至计算得到的圆弧半径与已知靶球半径差值的相对值满足迭代条件，此时六自由度工业机器人各关节轴的码盘数，以及激光器坐标系下计算出的圆弧圆心坐标，形成一个共轭对，同时程序自动保存本次寻优得到的机器人各关节轴的码盘数和圆弧圆心坐标，以供后续计算，如图3所示。

(5)在工业机器人形成前一个共轭对的最终姿态的基础上，按照标定程序的设定，自动控制机器人至下一个姿态，重复(2)-(4)的过程，形成后续所需要的多个共轭对，并且程序自动保存共轭对；

(6)在程序计算所须的N个共轭对的基础上，软件后台就可以计算出激光器坐标系与工业机器人末端法兰坐标系相对变换矩阵，即完成手眼标定。

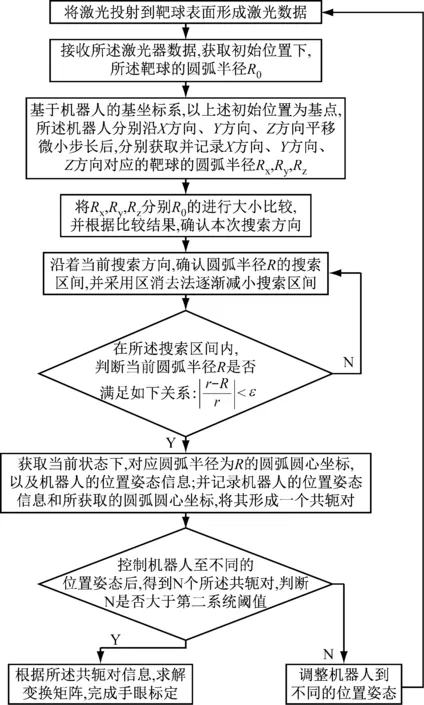
图3 自动寻优建立共轭对的流程图

3 总结

1.通过简单的搜索寻优过程，可以准确建立机器人位置姿态信息与靶球球心坐标的对应关系，方法便捷，自动化程度高。

2.可以应用到多种不同的标定相对变换矩阵的方法，既可以应用到将相对变换矩阵中的旋转分量与平移分量解耦，即通过沿工业机器人末端法兰坐标系平移来建立多个共轭对的情形，也可以应用到旋转分量与平移分量耦合在一起，同时求解的情形。通过该方法，手眼标定的精度可达0.05 mm以内，适用于一般精度的工业机器人应用，后续还可通过外部高精度测量补偿的方式进一步提高计算精度，应用与机器人高精度应用场合。

3. 本文所涉及的方法不需要外部精密的仪器，对工业机器人无精度要求，实用性强，适合工业现场应用。

[1] 王东署. 工业机器人标定技术研究[D]. 沈阳：东北大学， 2006.

[2] 刘振宇，陈英林，曲道奎，等，机器人标定技术研究[J]. 机器人，2002，24(5)：447-450.

[3] Hollerbach J M. A Survey of Kinematic Calibration: The Robotics review(1)[M]. Cambridge: MIT Press, 1989.

[4] Roth Z S, Mooring B W, Ravanir. An Overview of Robot Calibration[J]. IEEE Journal of Robotics and Automation. 1987, 3(5):377-385.

A Method of Establishment of Conjugate Pairs of End-Eye Calibration for Laser Measurement Robots

Shi Yu,Li Chunkai

(State ，China)

It is a very important topic to increase eye-end calibration accuracy for laser measurement robot. We present a method to establish conjugate pairs for eye-end calibration. By using calibrating vision coordination and TCP of robot a transformational matrix can be obtained. Because accurate sphere target with its diameter is known, it can be used to set up a conjugate pairs between position of robot and the center of the sphere.

Laser measurement robots; End-eye calibration; Conjugate pairs

郑 凯(1982-)，男，工程师，学士，研究方向：几何量精密测量技术研究。 金 路(1982-)，男，工程师，学士，研究方向：几何量精密测量技术研究。 梁金华(1976-)，女，高级工程师，学士，研究方向：几何量精密测量技术研究。

1007-757X(2017)04-0074-02

TP311

A

2016.10.05)