库水位变化和降雨条件下边坡渗流特性及稳定性分析
卢 博 郭永成 赵二平 龚章龙 汪 冲
(1. 三峡大学 三峡库区地质灾害教育部重点实验室,湖北 宜昌 443002; 2. 三峡大学 土木与建筑学院, 湖北 宜昌 443002)
库水位变化和降雨条件下边坡渗流特性及稳定性分析
卢 博1,2郭永成1,2赵二平1,2龚章龙1,2汪 冲1,2
(1. 三峡大学 三峡库区地质灾害教育部重点实验室,湖北 宜昌 443002; 2. 三峡大学 土木与建筑学院, 湖北 宜昌 443002)
我国西南地区地质构造复杂,降雨充足,地下水对岸坡稳定性的影响相对突出.以该地区某泄水建筑物进口边坡为原型,根据饱和-非饱和渗流理论和极限平衡理论,利用有限元分析软件Geo-Studio,对该边坡在不同降雨及水库水位升降条件下的渗流和稳定性进行了模拟计算.结果表明:边坡内的地下水位随库水位变动而变动,边坡的稳定性系数在库水位上升时先不断减小后缓慢增大;在库水位下降时先减小后逐渐增大,且下降速率越大,稳定性系数越小;在降雨入渗条件下,边坡的地下水位会有一定的抬升,同时边坡的稳定性系数相应减小.研究结果,可为边坡稳定性分析和水库安全运行提供可靠依据.
库水位升降; 降雨入渗; 地下水位; 渗流特性; 稳定性
我国可供开发的水能资源约为3.78×108kW,其中约68%分布在西南的青藏高原东缘地区[1].近年来,我国的水电建设迎来了高潮,而水电站多修建在地质条件较为复杂的地段,库岸边坡的稳定性问题越来越突出.
许多研究及统计资料[2-4]表明,影响库岸边坡稳定及失稳破坏的重要因素是地下水.其中周期性的库水升降和季节性降雨对边坡稳定性的影响较为显著,主要是其周期波动易引起边坡内的地下水位变化,引起边坡内的渗流场变化[2-3],并通过影响边坡中作为渗流骨架的岩体的力学性质来影响岸坡的稳定性[5].为合理确定地下水位,众多学者采用解析方法对其进行了研究[6-7],为了更好地符合地下水的实际影响情况,目前多采用数值模拟[8-10]的方法进行工程计算.本文以西南某在建水电站的进口边坡为例,结合前人的研究成果,运用饱和-非饱和渗流理论,对边坡在降雨和库水位变化条件下的渗流场采用有限元分析软件Geo-Studio进行数值模拟,再结合极限平衡方法分析其在非稳定渗流作用下的稳定性.
1 工程概况
某水电站位于四川省雅江县境内的雅砻江干流上,以发电为主,装机容量为300×104kW,为一等大(Ⅰ)型工程,正常蓄水位为2 865.0 m,死水位为2 785.0 m.拟计算边坡位于坝前左岸处,布置有泄洪洞、放空洞、导流洞等泄水建筑物进水口,岩性以粉砂质板岩、变质粉砂岩夹粉砂质板岩及变质砂岩与板岩互层为主,岩层总体产状N55~90°W/SW∠55~85°;岩体由强风化层、弱风化强卸荷层、弱卸荷弱风化层及微-新基岩等组成,各岩层间多发育宽度不一的断层,且断裂、节理裂隙较发育[11].该边坡地下水空间形态表现为表部是孔隙和基岩裂隙水,下部为裂隙承压水;大气降水多补给潜水,且对地下水位的影响较显著.
2 计算基础
2.1 饱和-非饱和渗流理论
边坡体中的地下水位随着雨量及库水位变化而发生改变,易使岩体的浸润线不断上下改变,而分别处于非饱和状态、饱和状态.考虑降雨入渗时,常采用文献[12-15]中的数学模型,选取流入流出单元的水量变化等于其水量随时间的变化率[14],对岩体的饱和非饱和渗流问题进行离散求解.在二维非稳定流情况下,其饱和-非饱和渗流控制方程[16]为:
(1)
式中,hw为总水头;kwx、kwy分别表示在x和y方向上的渗透系数;ρw为水的密度;g为重力加速度;mw为比水容量;t为时间.
2.2 稳定性分析理论
根据库水升降及降雨入渗条件下边坡渗流场的计算结果,采用文献[9-10]中的抗剪强度理论,考虑其引起的岩体抗剪强度等的降低,计算位于地下水位以上非饱和带岩体的强度.对拟分析坡体的饱和带区域进行稳定性计算时,依照修正的Mohr-Coulomb强度准则,采用极限平衡理论及考虑非饱和强度变化的方法,计算边坡在不同渗流状况条件下的稳定性.
3 计算模型及计算条件
3.1 计算模型
依据该边坡的工程地质特征,岩体节理裂隙普遍发育,所选的某计算剖面的工程地质条件如图1所示.

图1 计算剖面工程地质图
采用弹塑性岩体材料模型及Mohr-Coulomb屈服准则,对模型进行适当简化,并划分为按一定尺寸生成的三角形和四边形单元网格,滑动面处细化处理,单元数6 947个,节点数7 010个(如图2所示).

图2 计算剖面划分模型图
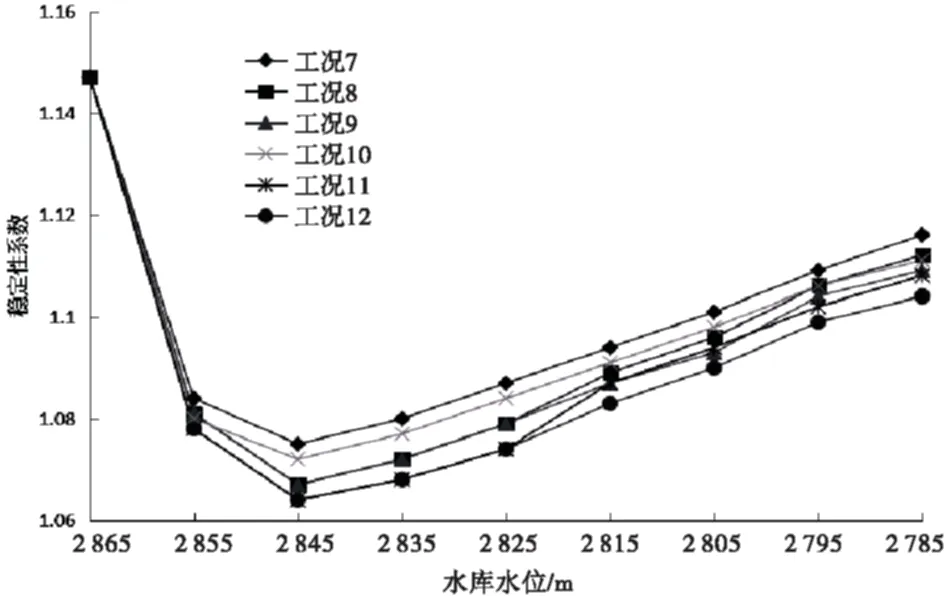
边坡模型以水平方向为X正轴,以垂直方向为Y轴,其范围为0 蓄水时,右侧水头为正常蓄水位;库水下降时,右侧水位线以上为零流量边界,水位线以下的边坡前缘施加相应的下降边界条件. 3.2 计算参数选取 按照风化卸荷线将边坡岩体分为:Ⅲ类、Ⅳ类及V类,并根据相关物理力学试验的结果,结合地层分布、勘探面风化界限、构造节理发育等情况,采用统计、综合分析和工程地质类比等方法,确定边坡岩体的物理力学参数见表1. 表1 边坡的物理力学参数 参照《水电水利工程边坡设计规范DL/T5353-2006》,该边坡的安全系数范围按规范要求选取,持久状况时为1.25~1.15,短暂状况时为1.15~1.05. 3.3 确定边界条件 考虑降雨边界条件时,需考虑持续降雨时的最大一次持续降雨量,并将其转化为软件中所需的流量边界,在边坡坡顶及蓄水位以上的坡面上建立流量与时间关系的边界条件,进行降雨入渗分析. 库水上升时,将库水位在2 785 m状态下计算得到的浸润线作为初始水位线,在模型上建立总水头上升高度与时间关系的外边界条件后,进行有限元计算;库水下降时,将稳定状态2 865 m水位时的浸润线作为初始水位线,建立总水头下降高度与时间关系的外边界条件,进行相关计算. 3.4 计算工况 由该地区的降雨统计资料[11]可知,雨季时多连续降雨,历史上最大日降雨量为70.6 mm.从工程安全的角度考虑,假定降雨为等强型且持续,拟将其按照强度为70 mm/d来考虑. 根据四川省径流特性、水电站群出力特点等,该水电站拟采用的调度方案为:每年6月初开始蓄水,8月初至9月底蓄至正常水位2 865.0 m;12月至次年5月末,坝前水位降至死水位2 785.0 m;6~7月的防洪限制水位为2 845.0 m[11]. 参照雅砻江干流上已建成水库的运行方式,结合该水库调度方案及边坡的工程地质特征,坝前水位上升速率拟取1 m/d、2 m/d等,下降速率拟取0.5 m/d、1 m/d等考虑,在边坡模型中设置表2中的几种工况的边界条件,计算在不同条件下的渗流及稳定性情况. 表2 边坡计算工况 注:工况2和工况5中,库水先期上升速率为2.0 m/d,历时20 d,后期上升速率为1.0 m/d,历时40 d;工况8和工况11中,库水先期下降速率为1.0 m/d,历时20 d,后期下降速率为0.5 m/d,历时40 d. 4.1 渗流计算分析 在边坡模型中,分别选取库水位为2 785 m、2 813 m、2 837 m、2 865 m时,对边坡内较有代表性的深部、中部及浅部部位的地下水位线进行分析,其在不同工况下的变化情况如图3~8所示. 库水上升条件下,以死水位2 785.0 m时的稳定渗流场作为初始渗流场,图3显示了库水上升时边坡内的地下水位变化情况. 从图3~4可知,在库水上升时,边坡体内的浸润线呈下凹状,地下水位也会随之上升.库水上升速度越快,其相应的地下水位越低,其中,上升速度为2.0 m/d时的地下水位最低. 从图5可知,边坡浅部的地下水位变化明显,与库水位同步变化;中部其次,深部最小,均呈滞后性. 图3 库水上升时典型地下水位情况 图4 库水上升时的不同工况下地下水位变化情况 图5 库水上升时边坡不同部位的地下水位线变化情况 注:库水上升时,将库水位为2 785 m时的地下水位线作为相对高程基准点,得出不同水位在不同工况下的相对高程值. 分析可知,当库水位逐渐上升时,库水会自外向坡体内部入渗,抬高地下水水位.库水上升速率越大,库水来不及完全入渗到边坡体内,坡体内的孔隙水压力不能与库水位完全同步抬升,使得坡内的地下水位线变化不明显.而越靠近岸坡的位置,其地下水位变化越明显,形成较大的水力坡度;远离岸坡位置的地下水位,则因渗透系数小及不能及时响应而变化较小,呈明显滞后性. 库水下降条件下,以正常水位2 865.0 m时的稳定渗流场作为初始渗流场,图6显示了库水下降时边坡内的地下水位变化情况. 从图6~7可知库水下降时,边坡体内的浸润线呈微上凸状,地下水位亦会随之下降.其中,工况8(下降速度为2.0 m/d与1.0 m/d结合)时的地下水位相对较低;而下降速度为2.0 m/d时的地下水位比下降速度为1.0 m/d时高. 图6 库水下降时典型地下水位情况 图7 库水下降时的不同工况下地下水位变化情况 从图8可知,边坡地下水浸润线滞后于库水位,其斜率呈增大趋势;浅部的地下水位与库水位变化同步且均比其他位置明显,深部最不明显.分析可知,由于边坡外层是含有碎石土等风化严重的岩体,导致边坡体内的地下水快速地向外渗出.库水下降速率越大,边坡体内的孔隙水因来不及排出,使其孔隙水压力与库水位不能完全同步降低,也使坡体内的地下水位线较高,再逐渐下降.靠近岸坡的位置,由于能及时响应库水的变化及渗透系数大,其地下水位比远离岸坡位置的地下水位变化明显. 图8 库水下降时边坡不同部位的地下水位线变化情况 注:库水下降时,将库水位为2 865 m时的地下水位线作为相对高程基准点,得出不同水位在不同工况下的相对高程值. 从图4~5、7~8可知,在库水升降与降雨联合作用条件下,降雨均会抬高坡体内的地下水位,尤其在库水下降时;并且此时边坡体内的总水头等值线与库水升降单独作用(即工况1~3及工况7~9)时的相似,总水头等值线没有发生较大的变化.这主要是由于此边坡岩体的渗透系数及降雨范围不大,导致降雨对边坡渗流场的影响及地下水位线的抬升不太明显.在降雨施加后的一段时间,边坡的地下水位会有一定幅度的变化.在远离岸坡位置的坡体内,其地下水位明显滞后于库水位,但降雨对地下水位的抬高作用比主要受库水影响的浅部更为明显. 4.2 稳定性计算结果与分析 在库水升降过程中,采用基于Mohr-Coulomb准则等的极限平衡法,对边坡相应滑体进行安全系数计算,并从其中找到安全系数最小的滑动面后,对其进行稳定性分析,其稳定性系数的变化情况如图9~10所示. 图9 库水位上升时稳定性系数的变化曲线图 从图9可知,在库水上升时,边坡的稳定性系数先持续减小,且起始在一定高程内快速减小,之后缓慢减小;当库水上升到一定高度(即稳定性系数最小)后,稳定性系数开始小幅度地上升而后趋于稳定.库水上升速率越大,到达同一库水位时所对应的边坡稳定性系数越大,且减小的速率越慢,最终的稳定性系数也越大. 图10 库水位下降时稳定性系数的变化曲线图 分析可知,库水逐渐上涨时,会自外向坡内渗透,抬高的地下水位对边坡岩体产生浮托力,降低了坡体的有效压力及最危险底滑面上的抗滑力等;从而使边坡滑面的稳定性系数在开始时降低.之后,边坡内外的水力坡降和指向坡内的渗透压力在不断增大,当指向坡内的动水渗透压力恰好抵消有效压力减小时,边坡滑面的稳定性系数达到最小值;而后稳定性均开始提高,待形成新稳定渗流场后稳定性系数也趋于稳定.库水上升速率越大,向坡体内部的渗透就相对越慢,产生的浮托力越大,使边坡稳定性减小得越快;在稳定性系数达到最小值后,指向坡内的动水渗透压力增大越快,边坡稳定性上升越快.故在库水上升速度为2.0 m/d时边坡稳定性系数减小较快;工况3时的最终稳定性系数上升最快. 从图10可知,在库水下降过程中,边坡的稳定性系数先快速减小;待库水下降到一定高度(即稳定系数达到最小值),稳定性系数开始逐渐增大,最后趋于稳定.库水下降速率越大,边坡在相同库水位时所对应的稳定性系数就越小,且减小速率越快;之后增大的速率越慢,最终的稳定性系数也越小.其中,库水下降速度为0.5 m/d时的边坡稳定性系数最大. 分析可知,当库水不断下降时,地下水响应的滞后,使坡内外的水位差不断增大,会产生向下的拖拽作用;坡内的地下水向外渗流,会增大坡体的重力和下滑力,导致边坡滑面的稳定性减小.在边坡稳定性达到最小后,坡体内的地下水仍在渗出,对岩体力学性质的软化作用不断减小,增大坡体最危险底滑面的抗滑力,使边坡的稳定性不断增大.库水下降速度越快,边坡的稳定性因孔隙水来不及排出而减小得越快.相反,在稳定性系数达到最小值后,坡体内的地下水能更充分地向坡外渗出,使坡体抗滑力及稳定性的上升速率越快.故在库水下降速度为0.5 m/d时边坡稳定性系数最大,工况7时的最终稳定性系数最大. 从图9~10可知,在库水升降与降雨联合作用条件下,雨水入渗使得降雨区岩体部分饱和,导致该区域坡体的抗剪强度等力学性质及有效应力均相应加快减小,最危险底滑面上的抗滑力下降,使边坡的稳定性系数均要比库水位升降单一作用(即工况1~3及工况7~9)时小,也会出现更小值.由于本边坡岩体类别的原因,地下水位变化滞后于库水位升降,而降雨范围不广,且坡内入渗较慢,因此降雨影响相对有限.这说明降雨不利于边坡稳定,但对边坡的稳定影响不如库水位变动明显.在降雨条件下,适当的库水升降的速率,将有助于提高边坡最终的稳定性. 1)库水位的升降速度及降雨入渗,均会对库岸边坡的渗流场及稳定性产生影响.本文依据饱和-非饱和渗流和极限平衡理论,利用有限元分析软件,对某泄水建筑物进口边坡在库水位升降和降雨条件下的渗流及稳定性进行了模拟与分析. 2)在单一的库水升降过程中,边坡的渗流场相似,且压力水头值变化趋势也相似.降雨对边坡渗流场的影响不太明显,但仍会抬升边坡的地下水位,尤其是深部边坡.在降雨与库水升降联合作用时,渗流场的水头等值线发生了改变,并改变了单一库水升降下的渗流场. 3)库水位变动及雨水入渗对边坡稳定性产生较大的影响,其中库水下降时比库水上升时的影响大,尤其是库水骤降.在持续降雨情况下,为确保该边坡的稳定,蓄水时先期速率可尽量大,到一定程度后,即边坡安全系数达到最小值后,蓄水的速率应尽量放慢,以使边坡的稳定性降低幅度最小;除控制库水位的升降速度及加强监测外,还应尽量避免发生库水骤降. [1] 黄润秋,王士天,胡卸文,等.澜沧江小湾水电站——高拱坝坝基重大工程地质问题研究[M].成都:西南交通大学出版社,1996. [2] 郑 慧,邵子叶,韩文喜,等.暴雨与库水位变化条件下晒盐坝滑坡渗流和稳定性数值模拟[J].地质灾害与环境保护,2012,23(1):58-63,95. [3] 刘广宁,黄波林,陈小婷,等.降雨和库水位升降对岩质岸坡的影响[J].长江流域资源与环境,2013,22(3):353-358. [4] 周永强,盛 谦.库水位变化和降雨作用下付家坪子高陡滑坡稳定性研究[J].长江科学院院报,2014,31(2):57-61,67. [5] 易 武,孟召平,易庆林.三峡库区滑坡预测理论与方法[M].北京:科学出版社,2011. [6] 冯文凯,石豫川,柴贺军,等.降雨及库水升降作用下地下水浸润线简化求解[J].成都理工大学学报(自然科学版),2006,33(1):90-94. [7] 吴 琼,唐辉明,王亮清,等.库水位升降联合降雨作用下库岸边坡中的浸润线研究[J].岩土力学,2009,30(10):3025-3031. [8] 王学武,冯学钢,王维早.库水位升降作用对库岸滑坡稳定性的影响研究[J].水土保持研究,2006,13(5):232-234,237. [9] 荣 冠,周创兵,江进辉,等.锦屏一级水电站左岸边坡渗流计算及稳定性分析[J].长江科学院院报,2005,22(6):49-53. [10] 朱 朋,卢书强,薛聪聪,等.库水位升降与降雨条件下滑坡的渗流及稳定性分析[J].长江科学院院报,2015,32(11):87-92. [11] 中国水电顾问集团成都勘测设计研究院.两河口枢纽布置工程地质报告[R].成都:中国水电顾问集团成都勘测设计研究院,2007. [12] 周家文,徐卫亚,邓俊晔,等.降雨入渗条件下边坡的稳定性分析[J].水利学报,2008,39(9):1066-1073. [13] 张 卓,练继建,杨晓慧,等.岩质边坡在降雨条件下的稳定性分析[J].哈尔滨工业大学学报,2009,41(10):202-205. [14] 刘建华,查旭东,付宏渊,等.考虑降雨入渗条件下岩质边坡稳定性分析[J].公路交通科技,2009,26(10):33-37,43. [15] 史绪鑫,张永彬.降雨入渗对裂隙岩质边坡稳定性的影响[J].济南大学学报(自然科学版),2014,28(6):429-433. [16] 朱岳明,龚道勇.三维饱和非饱和渗流场求解及其逸出面边界条件处理[J].水科学进展,2003,14(1):67-71. [责任编辑 周文凯] Analysis of Seepage Characteristics and Stability of a Slope under Conditions of Reservoir Water Level Fluctuation and Rainfall Lu Bo1,2Guo Yongcheng1,2Zhao Erping1,2Gong Zhanglong1,2Wang Chong1,2 (1. Key Laboratory of Geological Hazards on Three Gorges Reservoir Area, Ministry of Education, China Three Gorges Univ., Yichang 443002, China; 2. College of Civil Engineering & Architecture, China Three Gorges Univ., Yichang 443002, China) In Southwest of China, the geological structure is complex and the rainfall is abundant; so the influence of groundwater on the stability of reservoir slopes is relatively prominent. Taking an inlet slope of the discharge structure in that area as the prototype, the seepage and stability of the slope under different conditions of rainfall and the reservoir water level fluctuation are simulatively calculated based on saturated-unsaturated seepage theory, limit equilibrium theory and the finite element analysis software (Geo-Studio). The calculation results show that the groundwater level of the slope changes exactly in accordance with the reservoir water level, slope stability safety factor firstly decreases with the rise of reservoir water level, and then increases slowly. When the reservoir water level drops, the slope stability safely factor coefficient firstly decreases and then increases; and the lower the rate of decline is, the smaller the stability safety factor will be. Under the condition of rainfall infiltration, the groundwater level of the slope will rise to a certain extent; and the stability safety factor of the slope accordingly decreases at the same time. The research results can provide a reliable basis for slope stability analysis and the safe operation of the reservoir. reservoir water level fluctuation; rainfall infiltration; groundwater levels; seepage characteristics; stability 2016-10-28 国家自然科学基金重点项目(51439003);湖北省自然科学基金项目(2014CFC1139,2015CFC831);三峡库区地质灾害教育部重点实验室(三峡大学)开放研究基金项目(2015KDZ17);三峡大学科学基金(KJ2013B004) 郭永成(1980-),男,副教授,博士,主要研究方向为岩土工程、风险管理等.E-mail:ych_guo@126.com 10.13393/j.cnki.issn.1672-948X.2017.02.012 TV139.14: P642 A 1672-948X(2017)02-0054-06

4 边坡渗流及稳定性分析







5 结 论

