动力锂电池折旧率的规律研究
郝宁,马超,樊浩,孙耀芹,高泽恒
(1.国网冀北电力有限公司技能培训中心,河北 保定 071000;2. 国网冀北电力有限公司唐山供电公司,河北 唐山 063000)
动力锂电池折旧率的规律研究
郝宁1,马超1,樊浩1,孙耀芹1,高泽恒2
(1.国网冀北电力有限公司技能培训中心,河北 保定 071000;2. 国网冀北电力有限公司唐山供电公司,河北 唐山 063000)
碳酸铁锂电池在使用过程中,各项参数会发生规律性变化,其折旧率的规律是反映锂电池能量的重要指标。通过建立电池模型,研究了锂电池剩余电量的估计方法,列举了常见的电池SOC(电池的荷电状态,State of Charge)的估计方法,分析了各种方法的优点和局限性,提出基于人工神经网络模型的SOC预测方法,并在车仿真软件ADVISOR上进行仿真分析。最后通过动力电池SOC的仿真结果,给出了电动汽车动力电池SOH(电池的寿命状态,State of Health)的预测方法,提出通过曲线拟合模型进行预测,得出电池衰减速度的规律。
锂电池;折旧率;荷电状态;人工神经网络;寿命状态
0 引 言
以石油资源为代表的传统能源由于资源限制和环境污染等问题,正受到各类清洁能源的挑战。电动汽车以节能、环保等特点,已经成为当下研究的热点。
动力电池作为主要的储能元件,是制约电动汽车发展的重要因素之一。作为低碳行业发展的核心,动力锂电池具备比能量和比功率高的优点,也是我国生产较多的一种动力电池。
锂电池属于化学反应电池,其反应机理复杂,副反应多,通常需要对其特定指标来进行分析。锂电池的折旧率包括电池寿命和剩余容量,是反映其能量的重要参数。本文将建立锂电池模型,总结已有文献提出的折旧率规律的预测方法,并提出基于曲线拟合模型的预测方法和基于人工神经网络模型的动力电池SOC预测,进行仿真分析,反映锂电池的基本特性和折旧率的规律。
1 动力锂电池建模
动力电池的等效电路模型是利用RC的各种组合描述电池外部特性,包括线性模型、Thevenin模型、四阶动态模型和Massimo ceraolo动态模型等模型[1]。本文建立了基于电子运动理论的等效电路模型,该模型考虑了锂电池内部的化学反应,利用MATLAB进行参数辨识,可以辨识出电池模型中的欧姆内阻和极化内阻。
由电学元件的基本性质我们可以将电极上的极化现象等效成一个电容元件。当有电压加到电容两端时,会造成电容内部的电荷积累,产生了“极化”作用;将“去极化作用”等效成一个电阻,整个电极等效成电容和电阻并联的一个复合元件。
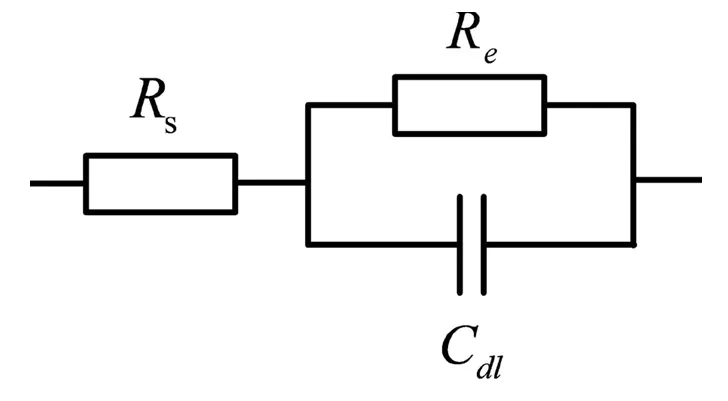
图1 基于电子运动 理论的电极阻抗模型
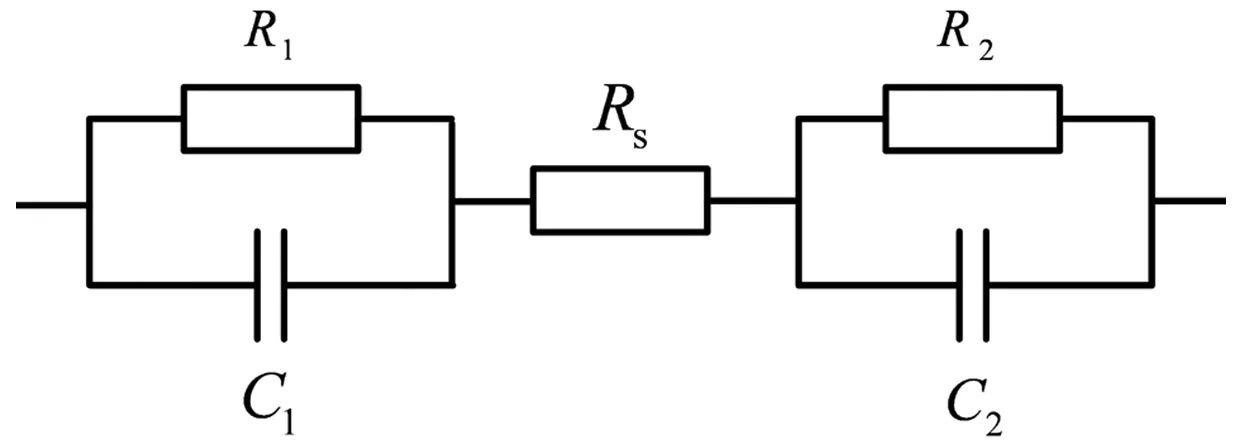
图2 双电极二阶RC等效电路模型
当有电压加到电极上时,电容产生电荷积累,同时又通过电阻对电容进行“放电”,产生一定的“去极化”作用,但由于外加电压的存在,使得“极化”作用占优势,这个复合元件正好起到了电极的作用。当充电或放电结束时,电池的电压会有个相反方向的下降或上升,也是这一复合元件的作用。我们将电解液的溶液电阻考虑在内,如图1为电极系统的等效电路。
图1中Cdl代表电极的极化电容,即双层电容;Re代表极化电阻,Rs代表欧姆内阻。由于电池由正负极两极组成,所以基于电子运动理论的电池等效电路中应该包含两个电极系统,等效电路如图2所示。
2 动力电池的剩余容量研究
剩余电量是指从当前时刻起,某个电池内部通过化学反应所能释放出来的电荷量。电池剩余容量的影响因素较多,主要包括充/放电倍率、自放电、环境温度、电池老化以及电池工作状态等[2]。这些影响因素的存在就是剩余电量的SOC预测较困难的主要原因。
国内外普遍采用荷电状态SOC来表征电池的剩余容量,表示形式如下[3]:
(1)
式中Qrated为电池的标称(额定)的电荷容量,Qramain为电池中剩余的电荷余量。
2.1 基于人工神经网络模型的动力电池SOC预测
本文在ADVISOR软件上搭建了某国产汽车的仿真平台,整车主要技术参数如表1所示[4]
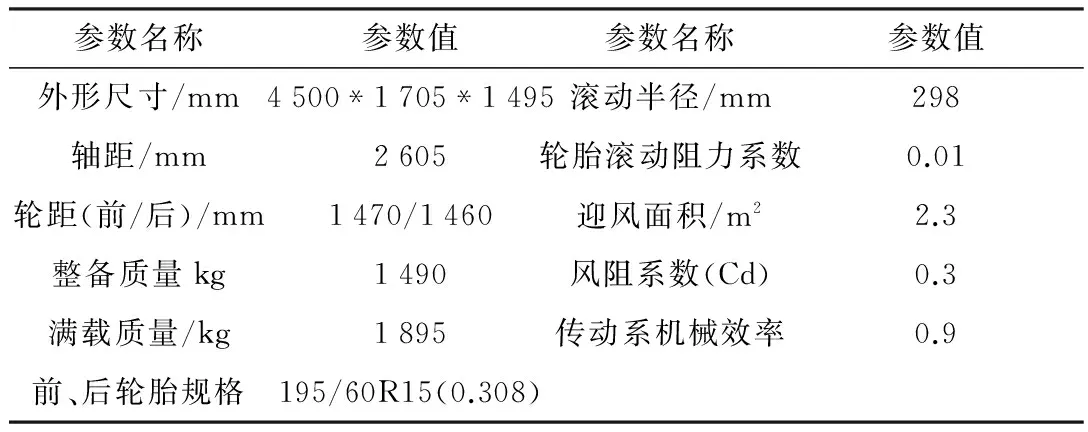
表1 整车主要技术参数
电动汽车仿真机构图由车轮/车轴(Wheel/Axle)、主减速器(Final drive)、能量存储系统(Energy Storage System)、锂离子电池和电动机(Motor)组成,如图3所示。
由于实际路况复杂多样,为了能更实际的反应汽车在路面上运行的状态,以对实际车辆进行跟踪测试的实验数据为基础[5-6],各个国家都制定了典型的循环行驶实验工况,来模拟车辆的运行工况。仿真中考虑这些工况:
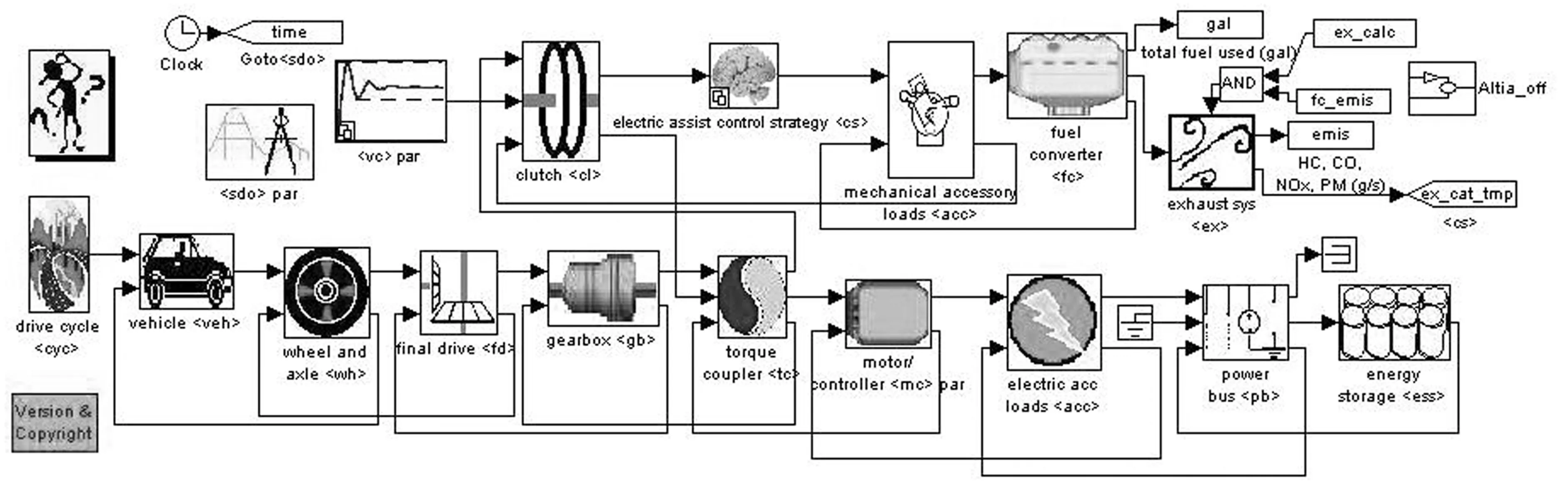
图3 电动仿真机构图
(1)ECE工况
ECE工况为欧洲用来测试城市低速道路下车辆性能的循环工况,其循环时间为195 s,行驶路程为0.99 km,最高车速为50 km/h,平均车速为18.26 km/h,最大加速度为1.06 m/s2,最大减速度为-0.83 m/s2,停靠次数为3次,速度-时间曲线如图4所示。
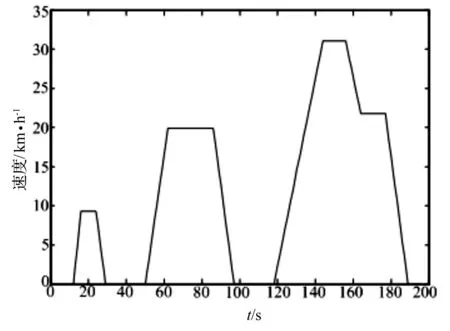
图4 ECE速度-时间曲线图
(2)UDDS工况
UDDS(Urban Dynamometer Driving Schedule)工况由美国环境保护署EPA制定的、用来测试车辆在城市道路下行驶的各种性能的循环工况。其循环时间为1 367 s,行驶路程为11.99 km,最高车速为91.25 km/h,平均车速为31.51 km/h,最大加速度为1.48 m/s2,最大减速度为-1.48 m/s2,停靠次数为17次,其速度-时间曲线图如图5所示。
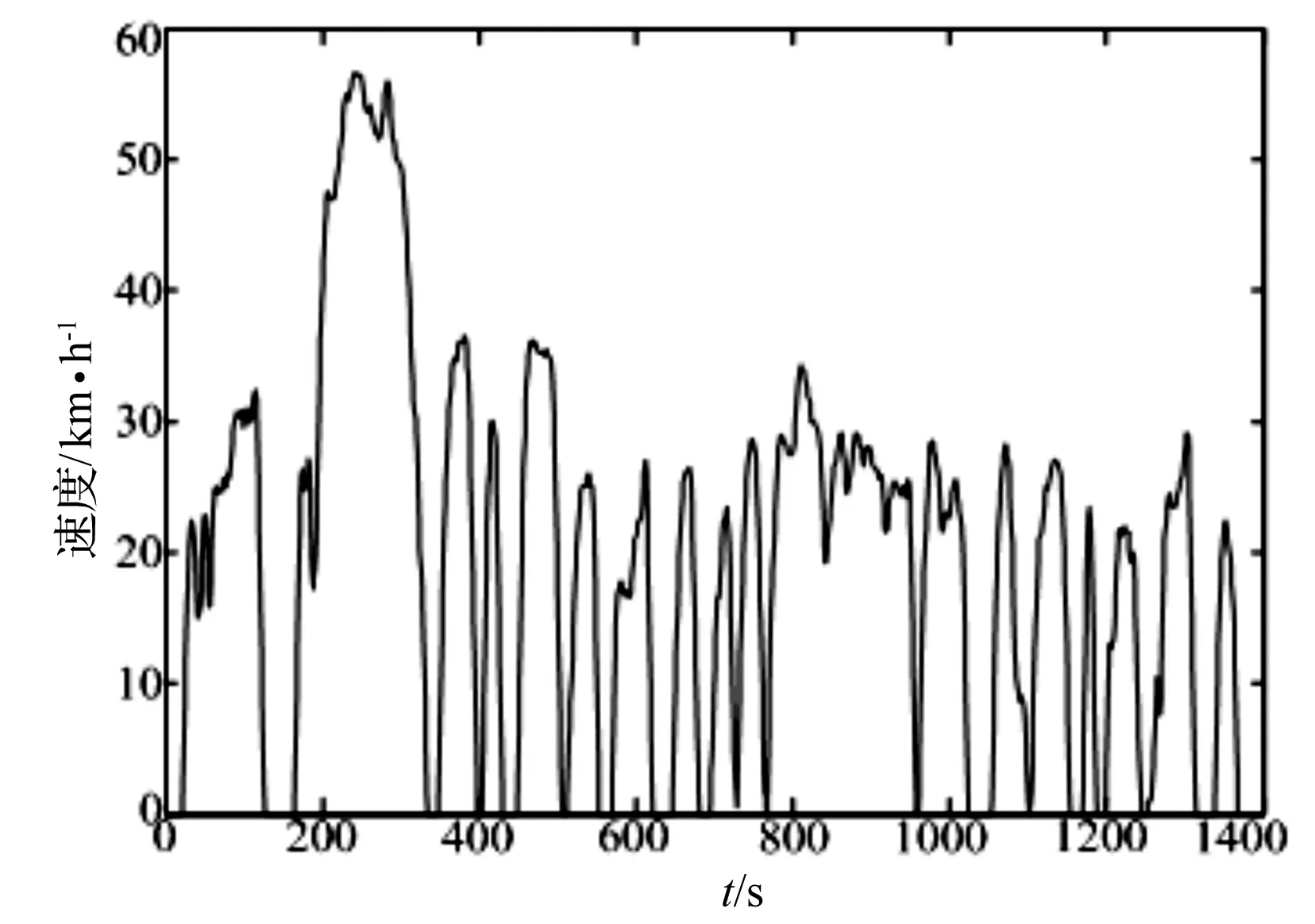
图5 UDDS速度-时间曲线图
(3)HWFET工况
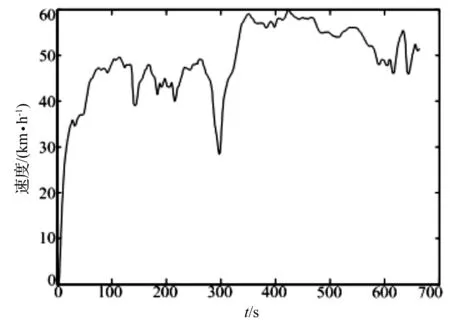
图6 HWFET速度-时间曲线图
HWFET(High Way Fuel Economy Test)工况是由美国环境保护署EPA制订的,用来测试高速道路上车辆性能的循环工况。其循环时间为765 s,行驶路程为1.51 km,最高车速为96.4 km/h,平均车速为77.85 km/h,最大加速度为1.43 m/s2,最大减速度为-1.48 m/s2,停靠次数为1次。如图6所示。
2.2 仿真结果
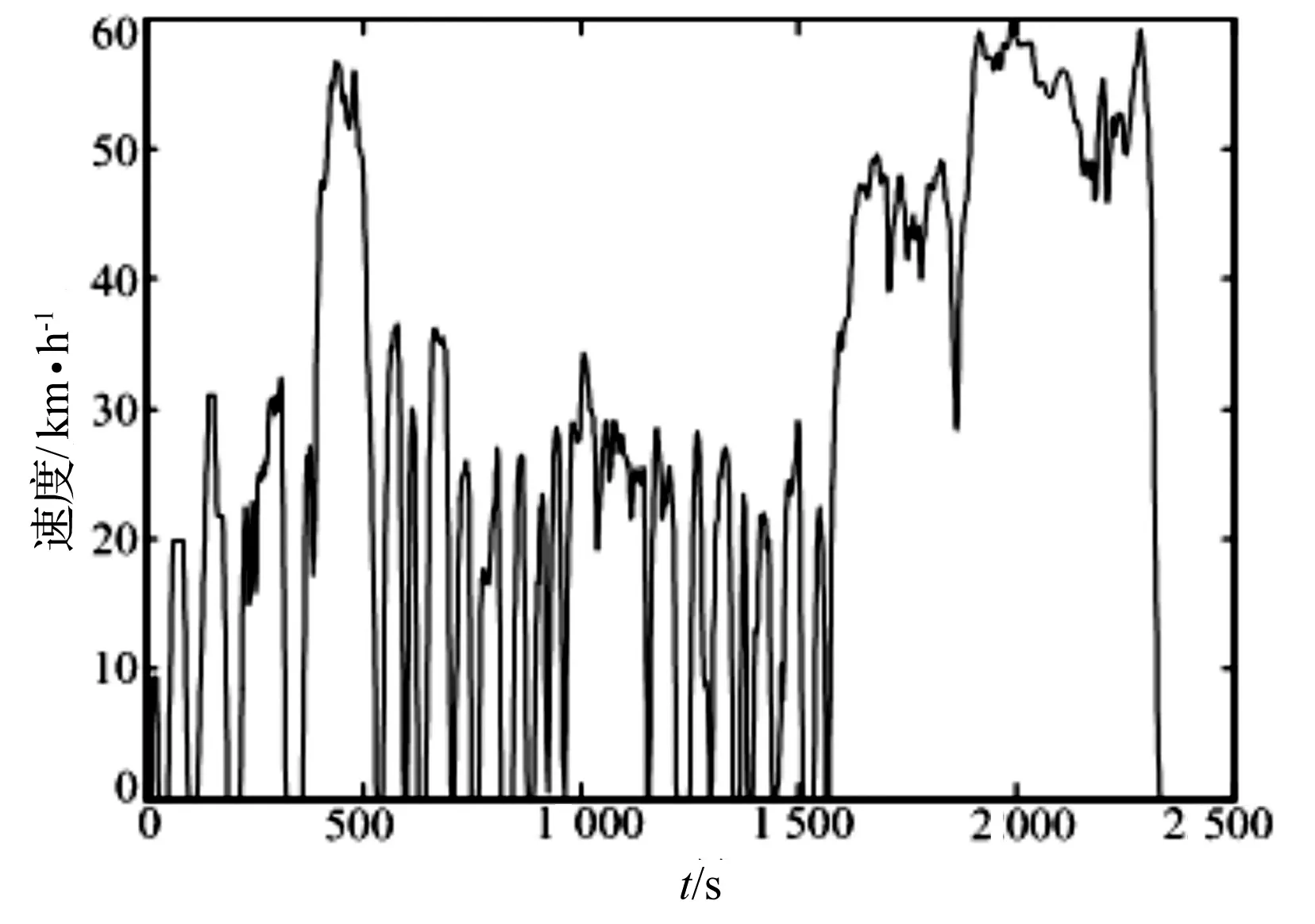
图7 速度-时间曲线图
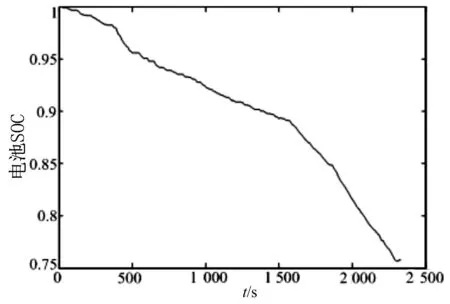
图8 电池SOC
仿真中将三种循环工况结合起来,来模拟汽车在道路上的实际运行工况,即汽车处于低速起步阶段、城市运行阶段和城郊高速运行阶段。采用纯电动汽车,汽车采用锂电池组,其他参数按照表1中的参数进行设计。图7为三种循环工况结合的速度-时间曲线图。仿真输出得到的锂电池的SOC如图8所示,电池的充放电电流如图9所示,电池的充电和放电效率分别如图10、图11所示。
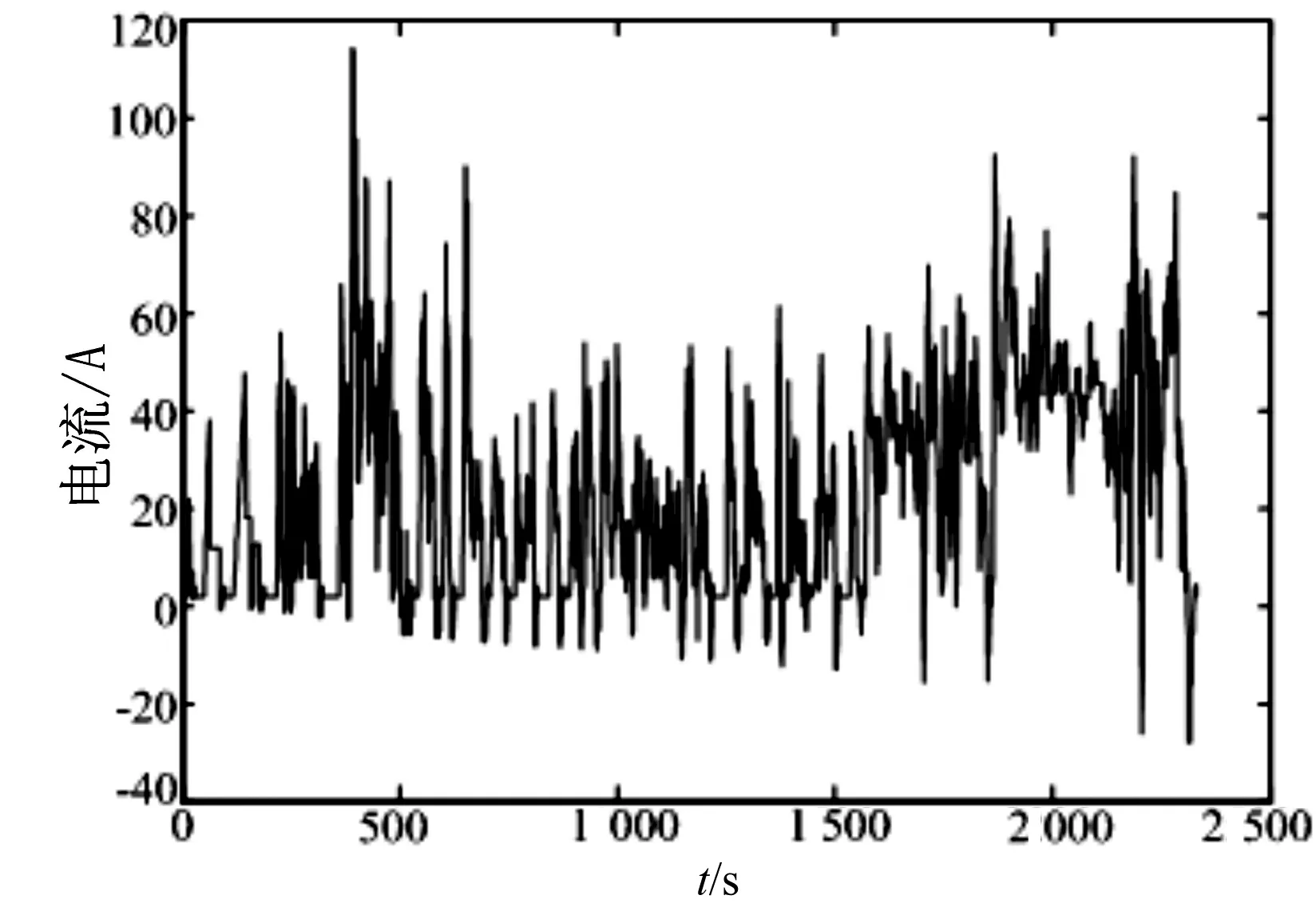
图9 电池电流曲线图
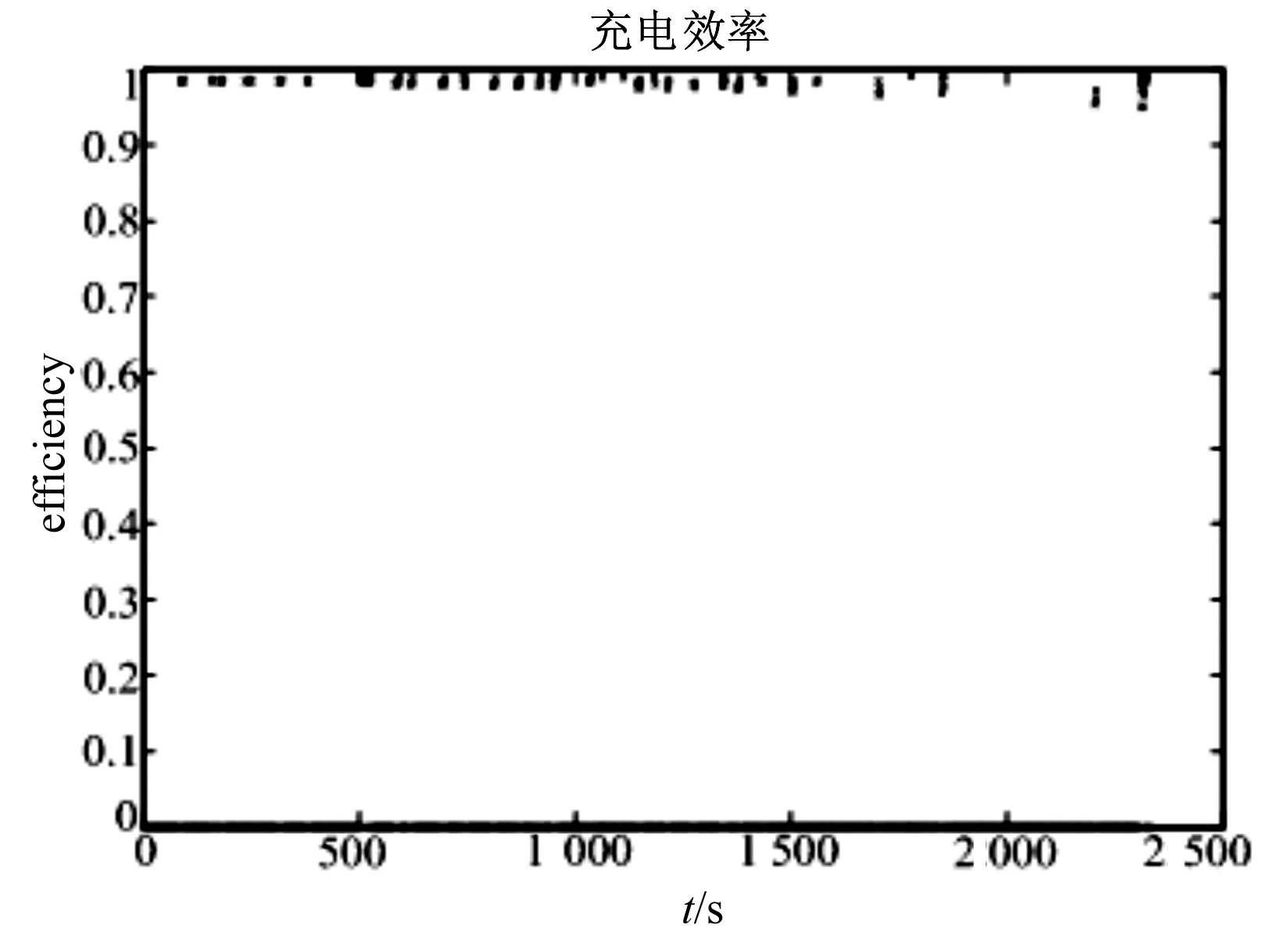
图10 电池充电效率图
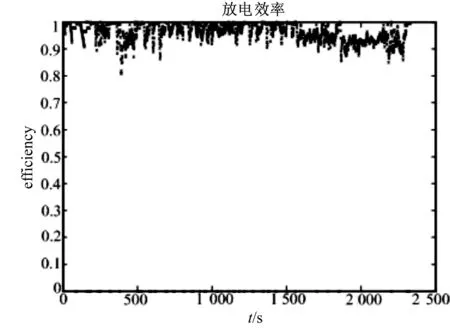
图11 电池放电效率图
3 动力电池的寿命研究
动力电池的寿命状态也可称为健康状况(State of Health, SOH),是电池寿命状态的表征参数,其标准定义是在标准条件下动力电池从充满状态以一定倍率放电到截止电压所放出的容量与其所对应的标称容量的比值,该比值反映了电池健康的一种状况:
(2)
式中Qaged为电池使用一段时间后测量的最大可用容量,Qnew为电池未使用时的最大容量。
一般认为电池实际的容量降到额定容量的80%时[7-8],此时电池就不可靠,可以认为电池的寿命已经终结。当电池的SOH达到0.8时,计此时电池循环充放电的次数,就是电池的循环寿命。
3.1 基于容量衰减的循环寿命预测
文献[9]根据第一性原理提出预测电池容量衰退的循环寿命半经验模型,通过SOC、SEI膜电阻和扩散系数的变化来定量研究电池循环容量的衰减。这一模型可以模拟出锂电池在不同循环次数时的放电曲线及容量,但没有考虑放电深度及温度对电池寿命的影响,这些都限制了其在动力电池寿命预测中的应用。
文献[10]根据可靠性试验理论和加速寿命试验的基本原理,以温度和充放电电流为加速应力,提出了电池容量衰退的修正模型:
(3)
式中Cr为容量衰减率;nc为循环次数;I为放电电流。
3.2 基于SOH估计的循环寿命预测
根据上文的分析可知,电池的健康状态SOH反应了电池的预期寿命。对动力电池SOH的估计可以预测出动力电池的循环寿命。
文献[11]提出了一种基于自适应数字滤波算法的电池内部状态估计的方法,该算法实际上使用的是一个递推的最小二乘法,其算法原理如图12所示。
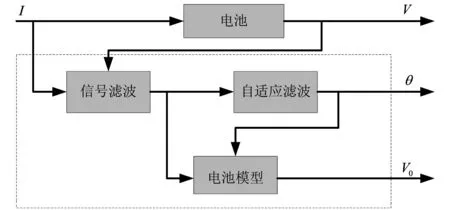
图12 自适应数字滤波估计SOH算法原理
基于以上算法的动力电池SOH估计,主要是通过对动力电池内部参数,如容量或内阻进行在线辨识实现。但是,这些参数除受电池老化过程影响外,还受到温度、工作电流、工作点等因素的影响,这严重影响了动力电池SOH的准确性,有时甚至带来估计的跳变。本文在下面采用的基于曲线拟合的动力电池寿命预测方法,考虑充放电电流、电池的温度等因素的影响。
3.3 基于曲线拟合模型的动力电池寿命预测方法
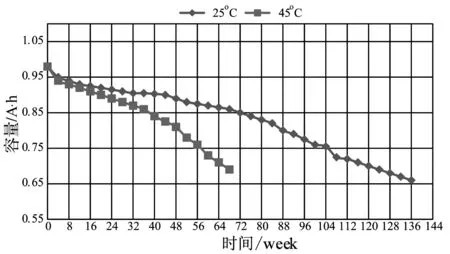
图13 不同温度下的放电容量图
根据文献[12]中提供的测试数据和试验方法,对锂电池的实验数据进行收集。实验所用的锂电池为18650型第二代动力锂电池,额定容量为1 Ah。循环寿命测试实验分别在25 ℃和45 ℃的温度条件下进行,放电电流大小为1 A。实验结果如图13所示。
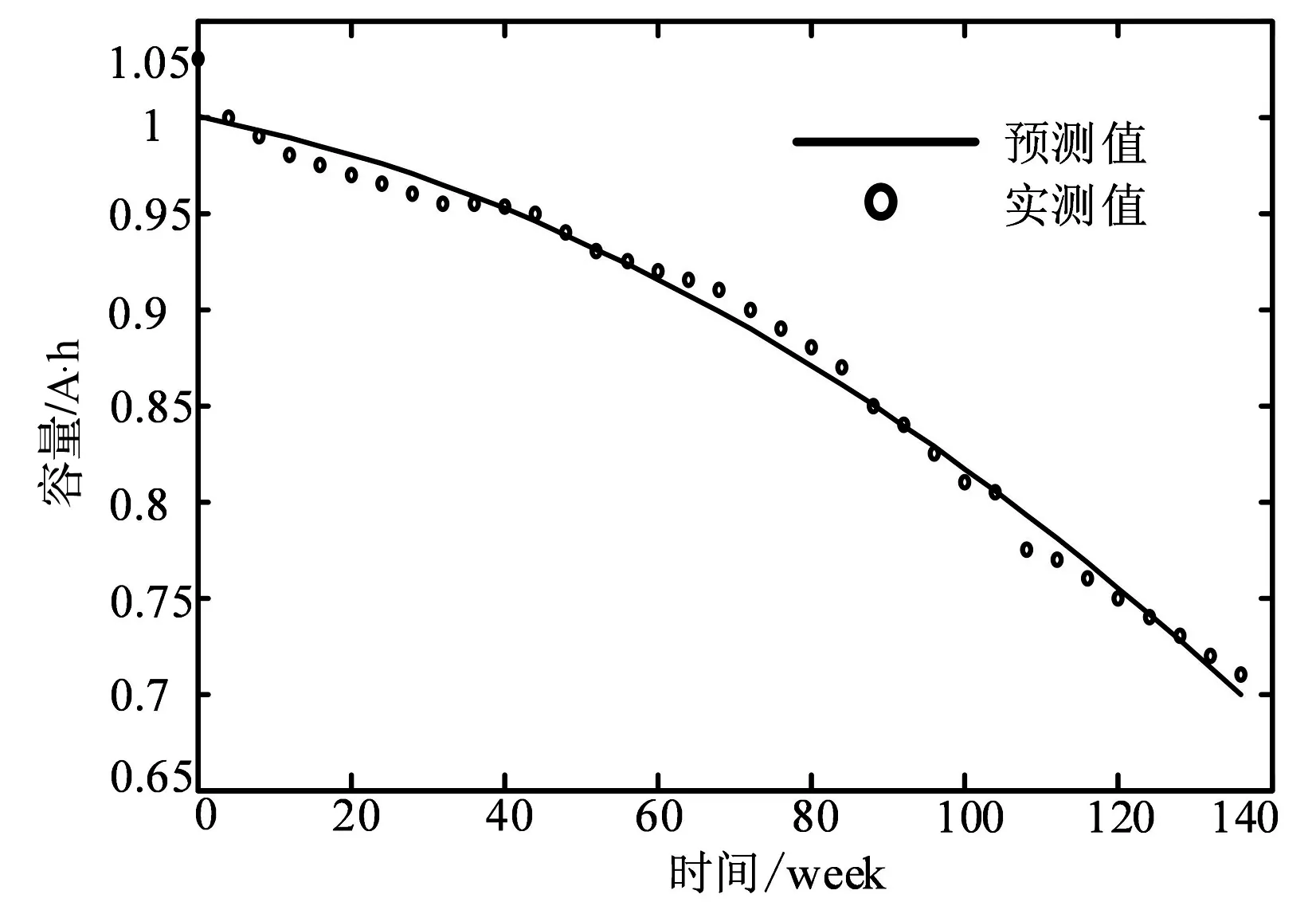
图14 25 ℃、1 A电流下电池容量 和循环次数关系图
本节利用最小二乘法对得到的实验数据进行拟合,得到的结果如下所示。图 14为温度为25 ℃时的预测曲线和实测值,式(3)为该种条件下的拟合曲线的公式。
y=-0.017 8x2-0.090 7x+0.8486
(3)
图15为温度为45℃条件下,电池的放电容量和循环寿命间的预测关系和实测值。式(4)为该种条件下的拟合关系曲线。
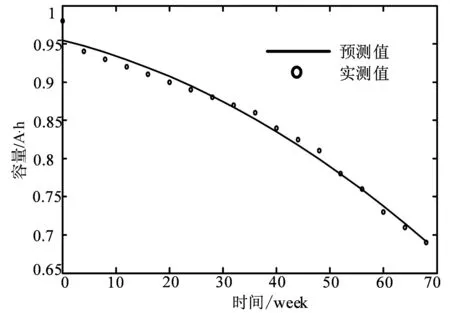
图15 45 ℃、1 A电流下电池容量和循环次数关系图
(4)
通过图可以看出,在45 ℃温度条件下,电池容量的衰减的速度比25 ℃温度下的容量的衰减速度。
4 结束语
由于电动汽车动力电池在使用过程中,动力电池的各项参数会出现规律性变化,因此本文对动力电池的折旧规律进行了研究。首先通过对磷酸铁锂电池的电池建模,得到了磷酸铁锂电池的电池的开路电压、欧姆电阻、极化电阻和极化电容与电池荷电状态之间的关系。其次研究了动力电池的剩余电量的估计方法,列举了常见的电池SOC的估计方法,分析了各种方法的优点和局限性。最后,基于汽车仿真软件ADVISOR的电池SOC仿真结果,给出了电动汽车动力电池的寿命的预测方法,分析了各种方法的优点和局限性。
[1] 王铭, 李建军, 吴扞, 等. 锂离子电池模型研究进展[J]. 电源技术, 2011, 35(7): 862-865.
[2] 段玲玲. 电动汽车锂电池组SOC预测研究[D]. 沈阳:沈阳理工大学, 2012.
[3] 孔庆, 王冬, 张治国. 电动汽车动力电池SOC估计研究综述[J]. 电气时代, 2012,31(10): 30-32.
[4] 汤桃峰. 电动车锂离子电池组SOC预估及一致性研究[D]. 重庆:重庆大学, 2011.
[5] 张俊智, 王丽芳. 驾驶循环对车辆能量经济性影响的研究[J]. 汽车工程, 2000, 22(5): 320-323.
[6] 李孟良, 朱西产, 张建伟, 等. 典型城市车辆行驶工况构成的研究[J]. 汽车工程, 2005, 27(5): 557-560.
[7] WENZL HEINZ, BARING GOULD IAN, KAISER RUDI,et al. Life prediction of batteries for selecting the technically most suitable and cost effective battery[J]. Journal of Power Sources, 2005, 144(2):373-384.
[8] SPOTNITZ R. Simulation of capacity fade in lithium-ion batteries[J]. Journal of PowerSources, 2003, 113(1):72-80.
[9] RAMADASS P, HARAN BALA, WHITE RALPH,et al. Mathematical modeling of the capacity fade of Li-ion cells[J]. Journal of Power Sources, 2003, 123(2):230-240.
[10] 黎火林, 苏金然. 锂离子电池循环寿命预计模型的研究[J]. 电源技术, 2008, 32(4): 242-246.
[11] NAKAMURA H, NAKAMURA H, YUMOTO D,et al. The application of adaptive digital filter for the internal state estimation of batteries[C].SICE 2003 Annual Conference, IEEE, 2003,2: 2239-2244.
[12] JON P. CHRISTOPHERSEN IRA BLOOM EDWARD V. Advanced technology development program for lithium ion batteries gen 2 performance evaluation final report[R]. 2006.
A Research on Regularity of Depreciation Rate of Power Lithium Batteries
Hao Ning1,Ma Chao1,Fan Hao1,Sun Yaoqin1,Gao Zeheng2
(1. State Grid North Hebei Electric Power Co. Ltd., Skill Training Center, Baoding Hebei 071000, China; 2. State Grid North Hebei Electric Power Co. Ltd., Tangshan Power Supply Co., Tangshan Hebei 063000, China)
During operation of iron carbonate lithium batteries, their parameters are changed regularly, and depreciation rate rule is an important index reflecting the energy capacity of the battery. Through establishment of a battery model, this article studies the methods for estimating remaining capacity of the lithium battery. Estimation methods for common SOC (state of charge) batteries are enumerated, and advantages and limitations of various methods are analyzed. Then, it presents an estimation method based on the artificial neural network model. Simulation analysis is made through ADVISOR aboard simulation software. Finally, with the help of the simulation results of the SOC power battery, it gives an estimation method for the SOH (state of health) of the vehicle power battery. It proposes that prediction should be made through a curve-fitting model to obtain the regularity of delay rate of the battery.
lithium battery;depreciation rate; state of charge; artificial neural network; state of health
10.3969/j.issn.1000-3886.2017.02.016
TM911
A
1000-3886(2017)02-0052-04
郝宁(1985-),男,河北保定人,讲师,主要从事输配电线路方面的研究。
定稿日期: 2016-08-30

