南极普里兹湾海域湍流扩散系数估计

丁文祥,梁楚进*,廖光洪,高立宝

(1.卫星海洋环境动力学国家重点实验室,浙江 杭州 310012；2.国家海洋局 第二海洋研究所,浙江 杭州 310012；3.国家海洋局 第一海洋研究所,山东 青岛 266061)

南极普里兹湾海域湍流扩散系数估计

丁文祥1,2,梁楚进*1,2,廖光洪1,2,高立宝3

(1.卫星海洋环境动力学国家重点实验室,浙江 杭州 310012；2.国家海洋局 第二海洋研究所,浙江 杭州 310012；3.国家海洋局 第一海洋研究所,山东 青岛 266061)

基于Thorpe尺度方法,利用CTD数据,计算了南极普里兹湾海域的Thorpe尺度和湍流扩散系数,分析了观测区域(64°～69°S,66°～80°E)湍流翻转现象的强弱及分布。结果表明,在海底和地形粗糙区存在较大的Thorpe尺度(较强湍流翻转)和湍流扩散系数,湍流扩散系数最大值能达到10-2m2/s量级,比平坦开阔海洋高2～3个数量级,部分观测站位的湍流扩散系数和湍动能耗散率表现出大-小-大的垂向分布结构,总水深较深的区域尤为明显；深水区域的浮力频率在海表面到500 m层比较大,浅水区域该现象不明显；湍动能耗散率在(67.25°S,73°E)周围和经度为78°E的各站位都表现相对较大,能达到10-6w/kg量级,个别站位甚至能达到10-5w/kg量级。

普里兹湾；Thorpe尺度；湍流扩散系数; 湍动能耗散率

0 引言

早在上世纪60年代,MUNK[1]指出,为了维持深海层化结构的稳定,大洋的平均扩散系数至少需要达到10-4m2/s的量级。但在随后的观测实验中发现,在远离边界的大洋内区,其扩散系数仅为10-6～10-5m2/s量级[2-3],低于MUNK所指出的1～2个数量级。直至上世纪90年代之后,一些观测证实了强烈的跨密度混合发生在海底边界[4-6],特别是海槛、海山、海脊和海底峡谷,其扩散系数可达10-4m2/s,甚至更强。

经向翻转环流(MOC)对全球气候系统有着非常重要的影响,而南大洋在闭合经向翻转环流上扮演着非常重要的角色。湍流混合在控制海水物理属性、营养物输运、海水颗粒物浓度上起着非常重要的作用,研究普里兹湾的混合过程对于理解南大洋深层和底层水的产生以及MOC的结构有重要的帮助。之前对于南大洋的湍流混合的研究大部分集中于南大西洋,尤其是德雷克海峡和斯科舍海[7-10]。所有研究都发现强混合主要发生在拥有粗糙或陡峭地形的区域。例如,美国和英国科学家自2009年开始,在南大洋开展了等密度面和跨等密度面混合实验(简称DIMES),该研究集中在东南太平洋的德雷克海峡,观测表明在南大洋某些海域,尤其在南极绕极流经过的拥有粗糙地形的海域,内部的跨等密度面混合非常强烈[11]。

普里兹湾是南大洋最大的海湾之一,它地处世界最大的兰伯特冰川所占据的地堑末端的冰川入海处,拥有宽阔的大陆架、陡峭的陆架坡折、强的上层分层和同性质的深层海水,是我国进行南大洋科学考察的重点海域,我国的南极科考站中山站就建立在该海域附近。该海域海底地形复杂多变,水深变化特别大,存在陆坡、海底峡谷等地貌,复杂的地形条件与强劲的绕极流相互作用很可能发生强烈的跨密度面混合翻转。然而,该海域直接的湍流观测数据不多,对于该海域的湍流混合还缺乏充分了解。本文将基于对普利兹湾CTD调查资料的分析,估算该海域的湍流扩散系数,分析其强弱分布。

1 数据和方法

1.1 数据

本文所采用的温-盐-深(CTD)数据来自中国第29次南极考察在普里兹湾海域的调查航次,CTD调查时间为2013年1月31日到2013年3月3日之间,CTD观测仪器的型号为SBE911plus,其采样频率为24 Hz,仪器的下降速度在0.5～1.4 m/s之间。为了消除高频干扰和船舶移动等影响,根据常规方法,本文将观测的CTD原始数据处理成空间间隔为1 m的数据。水深数据来自http://www.ngdc.noaa.gov网站的etopo1数据,空间分辨率为1′×1′。计算地形粗糙度采用的方法是取某位置的水深与以该点为中心的方圆18 km区域水深的标准差为该位置的粗糙度。具体普里兹湾海域地形和站位分布如图1所示,共有5个断面,分别是经度约为70.5°E各站位(图中AK连线上的站位)组成的P1断面、经度约为73°E各站位(图中CD连线上的站位)组成的P2断面、经度约为75.5°E各站位(图中EF连线上的站位)组成的P3断面、经度约为78°E各站位(图中GH连线上的站位)组成的P4断面和纬度约为67.25°S各站位(图中BH连线上的站位)组成的P断面。

目前有几种间接的估计湍流扩散系数的方法,一是Thorpe尺度方法,其基本思想是从湍流翻转的产生和不稳定的理查德森数来显示出能量的变动；二是垂直波数能谱法,即基于波-波相互作用理论来计算内波垂直方向波数能谱,以此估算湍流扩散系数[12-13]。本文将采用Thorpe尺度方法。

图1 普里兹湾地形及站位分布图Fig.1 Topography of Prydz Bay and the related measuring stations

1.2 Thorpe尺度方法

Thorpe尺度(L)是一种垂直长度尺度,用于测量稳定分层流体中的湍流翻转,与重力不稳定有关[14]。在稳定的分层流体中,从海底到海面,它的密度(温度)剖面的密度(温度)值必定是从大(小)到小(大)排列的,如果存在密度(温度)翻转的发生,即密度(温度)较大(小)的值对应的深度比密度(温度)较小(大)的值对应的深度浅或反之,则认为是湍流扰动的结果[15-16],即发生了湍流翻转现象。本文研究的区域为极地区域,该海域密度主要受盐度主导,温度对重力不稳定的影响要小于密度,所以本文在计算Thorpe尺度时均选用密度剖面。

在实际应用中,Thorpe在1977年首先采用将观测到的密度剖面重新直接排序[14],得到了排序后的密度剖面,即形成了绝对稳定的分层流体密度剖面。Thorpe尺度定义为Thorpe位移的均方根：

(1)

其中：dρ为某一点在排序前后的深度差,n为数据点的个数,L为Thorpe尺度。

在实际的海洋中,要想精确计算出dρ,还受到两个因素的限制,一是观测噪声的影响,另一个是当地的平均密度梯度的影响。因此将对数据作一定的处理。在某一深度,当原始数据和排序后的数据在该深度对应的密度之差小于噪声δ,就令该深度的Thorpe位移dρ=0。根据FERRON et al的方法[17],对数据作进一步的处理。假设原始的密度剖面的密度为ρ,噪声为δ,将ρ通过如下的变换获得一个中间密度ρΙ：

(1)设原始密度剖面的第一个值为ρ1,第二个值为ρ2,以此类推。同理,设中间密度剖面第一个值为ρΙ1,第二个值为ρΙ2,以此类推。且设ρΙ1=ρ1。

(2)比较ρ2和ρ1,如果|ρ2-ρ1|<δ,则ρΙ2=ρΙ1；如果|ρ2-ρ1|≥δ,则找出这样一个整数n,使得(ρ1±nδ)-ρ2≤δ,且令ρΙ2=ρ1±nδ。

(3)比较ρ3和ρ1,如果|ρ3-ρ1|<δ,则ρΙ3=ρΙ1；如果|ρ3-ρ1|≥δ,则找出这样一个整数n,使得(ρ1±nδ)-ρ3≤δ,且令ρΙ3=ρ1±nδ。

(4)以此类推,得到所有的ρΙ值。

这种处理方式得出的结果跟第一个值ρ1有比较大的关系,为了削弱这种影响,我们也可以从下向上求中间值,得到一个新的中间密度剖面ρⅡ。最终的中间密度剖面ρM取二次计算结果的平均值[14],即ρM=(ρⅠ+ρⅡ)/2。这样得出ρM值后,以ρM值为初始值,对ρM值进行排序,计算Thorpe位移以及Thorpe尺度。

1.3 有效翻转验证

为了把外界因素对结果的影响减到最小,我们再次对数据作进一步处理。

在求中间密度剖面时,有一个向上和一个向下的中间密度剖面,当满足以下两个条件时,才认定为真实翻转[18]：

(1)两个剖面都包含有不稳定的密度梯度；

(2)在两个剖面中,至少有一个不稳定的密度梯度在两个剖面中对应的压力差在0.1 dbar以内。

传感器响应的残留影响也会产生一些无效的翻转,例如,由于传感器响应的不匹配会产生盐度异常,盐度的变化对密度影响较大,就会容易产生不真实的翻转。为了降低这种影响,先定义一个翻转率R0[18]：

R0=min(L+/L,L-/L)

(2)

密度剖面排序后,在某一段完整翻转中,L+表示dρ大于零的数据的个数,L-表示dρ小于零的数据的个数,L表示总的数据个数。显然,在一个完整的翻转中,dρ的总和等于零,但L+和L-却不一定是相等的,由于传感器响应残留产生一个极大值或极小值而引起的一段翻转,L+和L-的值会相差很大,对应的R0值就会很小。根据前人的经验,当R0<0.2时,这段翻转就被认为是无效翻转,不放入实际Lρ的计算中[18]。

1.4 湍流扩散系数计算

在Thorpe尺度提出之前,Ozmidov还提出过一种长度尺度,称为Ozmidov尺度(LO)[19]：

(3)

其中：ε为湍动能耗散率,N为浮力频率。LO是通过量纲分析得出来的长度,在统计平均中,LO等价于将一流体质点所有的动能转化为势能后,流体质点所升高的高度,它是分层流体中允许的最大翻转尺度。

LO是通过量纲分析得出的长度尺度,Lρ是来自实际测量得出的长度尺度,通过前人的研究,二者存在一定的线性关系。在季节性海洋温跃层中,LO=0.79(±0.4)Lρ[15]；在永久性的海洋温跃层中,LO=0.66(±0.27)Lρ[20]；在温度低于2 ℃的海水中,LO=0.95(±0.6)Lρ[17]。在此先设

LO=aLρ

(4)

湍流扩散系数的公式为：

(5)

其中：Γ为混合效率,表示湍动能转化成势能的比率,混合效率一般情况下取0.2。

结合公式(3)、(4)、(5),即可得出Kρ与Lρ之间的关系式：

(6)

因为在接下来要处理的数据中,温度都低于2 ℃,所以选取a=0.95,即Kρ与Lρ之间的关系为：

(7)

通过公式(7),就可以直接用Lρ来计算出湍流扩散系数。

由公式(5)和(6)可以得出ε关于Lρ的一个表达式：

(8)

2 数据分析及结果

按照上面介绍的方法,对各站位的CTD数据作了一定的处理,计算出Thorpe尺度(L)、湍流扩散系数(K)、浮力频率(N)、地形粗糙度和湍动能耗散率(ε)。

图2为(65.5°S,73.0°E)站位(图1中标注红色1的站位)的Thorpe尺度、湍流扩散系数、湍动能耗散率和浮力频率剖面。比较明显的是,K和L的相关性很强,如图2中L和K剖面图显示,L值较大的位置,对应的K值也相对较大,大体的变化趋势基本一致。在0～500 m的深度内,该站位的L、K和N都相对较大,在500 m以深,N变化不明显,而L和K值波动相对较大,约在1 600 m深度处存在最大值,即在深层水中,L对K的影响是显著的,N对K的影响相对较弱。该站位的ε值在0～500 m的深度内相对于500 m以深明显要大很多,ε在500 m以深要减小约3个数量级。上层较大的ε值显然是受到0～500 m深度上较大的N值的影响,在500 m以下ε值虽然相对较小,但变化趋势与L基本一致。

2.1 横向断面

图3显示了67.25°S纬度断面(图1中P断面)的Thorpe尺度、湍流扩散系数、湍动能耗散率、浮力频率和地形粗糙度。L、K和ε的分布比较相似,即有较大的L出现的位置,K和ε也会相对较大；L相对较小的位置,对应的K和ε也相对较小。在71°～73°E范围,在100～500 m水深之间存在较大的L、K和ε值,而在底部相对较小,即在该范围内中间层存在较强的湍流翻转现象。在73°～76°E范围，

图2 (65.5°S,73.0°E)站位(图1中红色1标注的站位)的Thorpe尺度(L)、湍流扩散系数(K)、湍动能耗散率(ε)和浮力频率(N)剖面图Fig.2 Thorpe scale profile(L), turbulent diffusivities profile(K), dissipation rate of turbulent kinetic energy profile(ε) and buoyancy frequency profile(N) of the station which located in the pint of (65.5°S，73.0°E)(marked with red 1 in Fig. 1)

在200 m以深位置存在较大的L、K和ε值,即在该范围内底层存在较强的湍流翻转现象。在76°E以西,L、K和ε值相对较小。在该纬度断面,水深相对较浅,N的剖面图并没有表现出上部较大,下部相对均匀的现象,且与L、K和ε值存在一定关系。如图3a～3d,73°～76°E的几个站位,在L、K和ε值较大的位置上,N值也相对较大,说明该区域,K和ε的分布是L和N共同作用的结果。在该纬度上,地形粗糙度的变化幅度不是很大,但在76°E位置有一个突起(图3e),在该位置附近的两个站位的L、K和ε值相对较大。

图3 P断面上各站位的Thorpe 尺度剖面(a)、湍流扩散系数剖面(b)、湍动能耗散率剖面(c)、浮力频率剖面(d)以及各站位所在位置的地形粗糙度(e)Fig.3 Thorpe scale (a), turbulent diffusivities(b), dissipation rate of turbulent kinetic energy(c),buoyancy frequency(d) and terrain roughness(e) profiles of the stations on the P section黑色实线为当地水深Black solid lines are the local water depths

2.2 纵向断面

图4～图8给出了各经向断面的Thorpe尺度、湍流扩散系数、湍动能耗散率、浮力频率以及地形粗糙度的分布情况(δ=0.000 5 kg/m3,黑色实线为当地水深)。

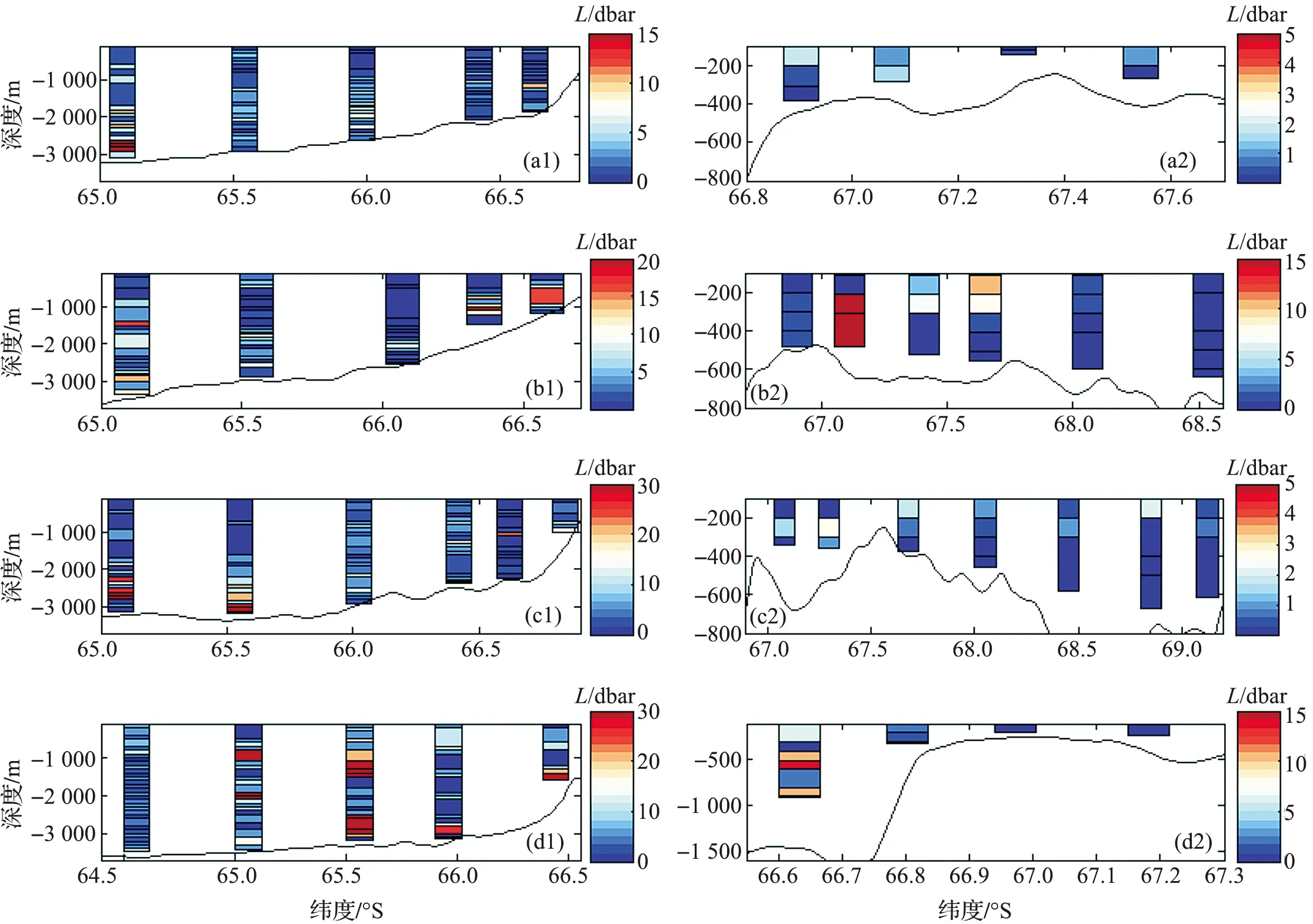
图4 P1～P4断面上各站位的Thorpe尺度剖面Fig.4 Thorpe scale profiles of the stations which are on the P1～P4 sectionsa1和a2为P1断面，b1和b2为P2断面，c1和c2为P3断面，d1和d2为P4断面；黑色实线为当地水深。图5～图7同此a1 and a2 are P1 section, b1 and b2 are P2 section, c1 and c2 are P3 section, d1 and d2 are P4 section.Black solid lines are the local water depths. Fig.5 to Fig.7 are the same

图5 P1～P4断面上各站位的湍流扩散系数剖面Fig.5 Turbulent diffusivities profiles of the stations which are on the P1～P4 sections

图6 P1～P4断面上各站位的湍动能耗散率剖面Fig.6 Dissipation rate of turbulent kinetic energy profiles of the stations which are on the P1～P4 sections

图7 P1～P4断面上各站位的浮力频率剖面Fig.7 Buoyancy frequency profiles of the stations which are on the P1～P4 sections

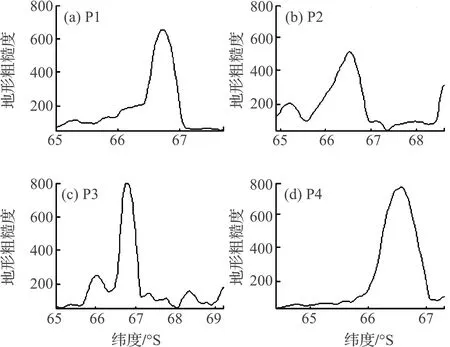
图8 P1～P4断面位置的地形粗糙度Fig.8 Terrain roughness of the P1～P4 sections

由上图可知,K、ε与L的分布相似,在总水深较深的区域尤为明显,出现较大L值的位置,K和ε值也会相对较大,即在该片区域K和ε受L影响较大。Thorpe尺度一般在海底部分和地形突变的地方存在较大值,而在总水深较浅的海域相对较小,即在深水底层和地形突变的区域存在较强的湍流翻转现象(图4～图6)。

浮力频率在总水深较深的区域(图7a1、7b1、7c1、7d1)海面到500 m层存在较大值,能达到10-3s-1,在500 m以深变化不大,平均为10-4s-1；而在总水深较浅的区域(图7a2、7b2、7c2、7d2),这种表层大,表层以下相对均匀的现象不明显,部分站位显示,总水深较浅区域的底部也存在较大的浮力频率。

如图5所示,在海底和地形突变的地方K值明显较大,最大值能达到10-2m2/s量级,在总水深较深的区域(图5a1、5b1、5c1、5d1),K值存在大-小-大的结构分布,在经度为78°E各站位(图5d1、5d2)尤为明显。MUENCH et al[21]在罗斯海、YANG et al[22]在普里兹湾也发现了同样的大-小-大湍流扩散系数的垂向分布结构。这可能是因为表层受较大的浮力频率的影响而相对较大,底层受较大的Thorpe尺度的影响而相对较大,从而形成了这种结构分布。而在总水深较浅的区域(图5a2、5b2、5c2、5d2),这种现象很不明显,这跟YANG et al[22]在普里兹湾发现的结果有点不同,原因可能是Thorpe尺度的方法不太适合埃默里冰架前缘海域,密度梯度相对较大,水深有限,Thorpe尺度方法受到一定限制。

湍动能耗散率(图6)总体表现出表层相对较大,这可能是受表层较大的浮力频率影响的结果,部分站位底层也有较大的ε值出现,在总水深较深的区域(图6a1、6b1、6c1、6d1),ε值也出现了大-小-大的分布结构,这与K值的分布相类似。而在总水深较浅的区域(图6a2、6b2、6c2、6d2),部分站位表现出上层ε值较大,下层分布相对均匀的现象,但ε值比较小。对全部站位的湍动能耗散率作垂向平均(图9),部分站位数据显示,湍动能耗散率能达到10-6w/kg量级,甚至个别站位能达到10-5w/kg量级,但大部分集中在10-7～10-9w/kg量级。湍动能耗散率较大的值一般分布在点(67.25°S,73°E)周围,在经度为78°E的各站位上,湍动能耗散率也相对较大。从地形粗糙度来看,地形粗糙度较大或地形粗糙度变化率较大的地方,湍动能耗散率也会相对较大。

图8为各站位所在区域的地形粗糙度,地形突变的地方,地形粗糙度明显变大,而在地形粗糙度较大的地方,湍流翻转现象也较为明显,对应的湍流扩散系数和湍动能耗散率也明显较大。湍流扩散系数的大小与当地的地形粗糙度存在一定的联系,但并不是湍流扩散系数较大的地方,对应的地形粗糙度也一定较大,湍流扩散系数除了受地形的影响,还很可能与南极的绕极流以及当地的水团分布有关。黄奕普等[23]通过氘示踪的方法研究普里兹湾海域的水团和环流时发现,在73°E、67°S稍南有个低δD水团,稍北有个高δD水团,67°S为两水团的分水岭。在68°S以南,75°E以东也存在一个高δD水团,受阻于西边的低δD水团而止于74°E处。即73°E、67°S附近是该海域3种不同水团的交汇处,而且附近的深水槽是普里兹湾与外海水交换的主要通道,这可能是该位置出现较大的湍动能耗散率的主要原因。NUMES et al[24]通过分析普里兹湾海域的水文数据来研究该海域的水平环流,在200 m以浅,普里兹湾的水体输入主要由其内缘东侧的沿岸流维系,200 m以深则是受67°S以北绕极深层水上涌入侵,这可能是经度为78°E的各站位在67°S以北出现较大湍动能耗散率的一个重要原因,以及深水区域,即67°S以北海域站位的底部均出现较大的湍流扩散系数可能也与该区域深层水上涌有关。

图9 各站位湍动能耗散率的垂向积分和当地地形粗糙度Fig.9 The vertical integration of dissipation rate of turbulent kinetic energy at all stations and the terrain roughness等值线为地形粗糙度The contours are terrain roughness

3 结论

本文利用南极普里兹湾海域调查的CTD资料,基于Thorpe的方法优化后来计算Thorpe尺度,再利用Thorpe尺度计算湍流扩散系数,估计了该海域湍流扩散系数的大小及湍流翻转的分布,结果表明：

(1)该海域存在较强的湍流翻转现象,湍流扩散系数最大值能达到10-2m2/s量级,湍动能耗散率能达到10-6w·kg-1量级。

(2)Thorpe尺度、湍流扩散系数和湍动能耗散率在海底和地形突变地带比较大。在总水深较深区域,浮力频率在海表面附近较大,500 m以下分布相对均匀；而在总水深较浅区域,该现象不明显。

(3)湍流扩散系数和湍动能耗散率在总水深较深的水域都有表现出大-小-大的垂向分布结构。

(4)在(67.25°S,73°E)周围以及经度为78°E的各站位,湍动能耗散率相对较大。

(5)地形粗糙度相对较大的区域,对应的Thorpe尺度和湍流扩散系数也相对较大,但并非完全一致,湍流翻转还可能受到南极的绕极流以及当地水团分布的影响。

整个普里兹湾海域都存在明显的湍流翻转现象,湍流扩散系数和湍动能耗散率相对开阔大洋都较大,这与当地的地形、水团以及海流等都有关。目前对于该海域的研究还非常有限,对于普利兹湾海域的湍流空间分布及其形成原因还需要更多的观测和模式来做更深入的研究。

[1] MUNK W H. Abyssal recipes[J].Deep Sea Research and Oceanographic Abstracts,1966,13(4):707-730.

[2] GREGG M C. Diapycnal mixing in the thermocline: A review[J]. Journal of Geophysical Research: Oceans (1978—2012),1987,92(C5):5 249-5 286.

[3] LEDWELL J R, WATSON A J, LAW C S. Evidence for slow mixing across the pycnocline from an open-ocean tracer-release experiment[J]. Nature,1993,364(6439):701-703.

[4] LUECK R G, MUDGE T D. Topographically induced mixing around a shallow seamount[J]. Science,1997,276(5320):1 831-1 833.

[5] POLZIN K L, TOOLE J M, LEDWELL J R, et al. Spatial variability of turbulent mixing in the abyssal ocean[J]. Science,1997,276(5309):93-96.

[6] CARTER G S, GREGG M C. Intense, variable mixing near the head of Monterey Submarine Canyon[J]. Journal of Physical Oceanography,2002,32(11):3 145-3 165.

[7] HEYWOOD K J, GARABATO A C N, STEVENS D P. High mixing rates in the abyssal Southern Ocean[J]. Nature,2002,415(6875):1 011-1 014.

[8] GARABATO A C N, POLZIN K L, KING B A, et al. Widespread intense turbulent mixing in the Southern Ocean[J]. Science,2004,303(5655):210-213.

[9] GARABATO A C N, STEVENS D P, WATSON A J, et al. Short-circuiting of the overturning circulation in the Antarctic Circumpolar Current[J]. Nature,2007,447(7141):194-197.

[10] SLOYAN B M. Spatial variability of mixing in the Southern Ocean[J]. Geophysical Research Letters,2005,32(18):doi:10.1029/2005GL023568.

[11] LEDWELL J R, St. LAURENT L C, GIRTON J B, et al. Diapycnal mixing in the Antarctic circumpolar current[J]. Journal of Physical Oceanography,2011,41(1):241-246.

[12] NAVEIRA GARABATO A C, OLIVER K I C, WATSON A J, et al. Turbulent diapycnal mixing in the Nordic seas[J]. Journal of Geophysical Research: Oceans,2004,109(C12010):doi:10.1029/2004JC002411.

[13] KUNZE E, FIRING E, HUMMON J M, et al. Global abyssal mixing inferred from lowered ADCP shear and CTD strain profiles[J]. Journal of Physical Oceanography,2006,36(8):1 553-1 576.

[14] THORPE S A. Turbulence and mixing in a Scottish loch[J]. Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences,1977,286(1334):125-181.

[15] DILLON T M. Vertical overturns: A comparison of Thorpe and Ozmidov length scales[J]. J Geophys Res,1982,87(C12):9 601-9 613.

[16] PARK Y H, FUDA J L, DURAND I, et al. Internal tides and vertical mixing over the Kerguelen Plateau[J]. Deep Sea Research Part II: Topical Studies in Oceanography,2008,55(5):582-593.

[17] FERRON B, MERCIER H, SPEER K, et al. Mixing in the Romanche fracture zone[J]. Journal of Physical Oceanography,1998,28(10):1 929-1 945.

[18] GARGETT A, GARNER T. Determining Thorpe scales from ship-lowered CTD density profiles[J]. Journal of Atmospheric and Oceanic Technology,2008,25(9):1 657-1 670.

[19] OZMIDOV R V. On the turbulent exchange in a stably stratified ocean[J]. Izv Acad Sci USSR, Atmos Oceanic Phys,1965,1(8):853-860.

[20] CRAWFORD W R. A comparison of length scales and decay times of turbulence in stably stratified flows[J]. Journal of Physical Oceanography,1986,16(11):1 847-1 854.

[21] MUENCH R, PADMAN L, GORDON A, et al. A dense water outflow from the Ross Sea, Antarctica: Mixing and the contribution of tides[J]. Journal of Marine Systems,2009,77(4):369-387.

[22] YANG Qing-xuan, TIAN Ji-wei, ZHAO Wei, et al. Turbulent dissipation and mixing in Prydz Bay[J]. Chinese Journal of Oceanology and Limnology,2013,31(2):445-453.

[23] HUANG Yi-pu, CAI Ping-he, CHEN Min, et al.Deuterium tracing study on water mass and circulation in Prydz Bay and its adjacent sea[M]//CHEN Li-qi.Study on the response and feedback of antarctic region to global change.Beijing:China Ocean Press,2004:59-71.

黄奕普,菜平河,陈敏,等.普里兹湾及临近海域水团、环流的氘示踪研究[M]//陈立奇.南极地区对全球变化的响应与反馈作用研究.北京：海洋出版社,2004:59-71.

[24] VAZ R A N, LENNON G W. Physical oceanography of the Prydz Bay region of Antarctic waters[J]. Deep Sea Research Part I: Oceanographic Research Papers,1996,43(5):603-641.

The turbulent diffusivity estimation in Prydz Bay,Antarctic

DING Wen-xiang1,2, LIANG Chu-jin*1,2, LIAO Guang-hong1,2, GAO Li-Bao3

(1.StateKeyLaboratoryofSatelliteOceanEnvironmentDynamics,Hangzhou310012,China;2.SecondInstituteofOceanography,SOA,Hangzhou310012,China; 3.TheFirstInstituteofOceanography,SOA,Qingdao266061,China)

Thorpe scale and turbulent diffusivities in Prydz Bay of Antarctica were calculated based on Thorpe method and Conductivity-Temperature-Depth data. The strength of turbulent overturn was analyzed and its spatial distribution was also investigated. The results show that the larger Thorpe scale and turbulent diffusivities occur in rough topographic area and near the sea floor, and the maximum value of turbulent diffusivities exceeds 10-2m2/s, which is about two or three orders of magnitude larger than that in the open ocean. Turbulent diffusivities and dissipation rate of turbulent kinetic energy show high-low-high vertical structure in some observational stations, especially in deep area. The larger values of buoyancy frequency appear in upper 500 m water column in deep area, but this phenomenon is not obvious in shallow area. The dissipation rates of turbulent kinetic energy in the stations around the point(67.25°S，73°E) and along the 78°E sections are quite large, which exceed 10-6w/kg, and even reach 10-5w/kg in a few stations.

Prydz Bay; Thorpe scale; turbulent diffusivities; dissipation rate of turbulent kinetic energy

10.3969/j.issn.1001-909X.2017.01.002.

2016-03-08

2016-10-10

南北极环境综合考察与评估专项项目资助(CHINARE 2015-01-01,CHINARE2016-04-01-01)；全球变化与海气相互作用专项项目资助(GASI-03-01-01-07)；国家自然科学基金项目资助(41376033)；国家海洋局第二海洋研究所基本科研业务费专项项目资助(SOEDZZ1517,SOEDZZ1519,JT1506)

丁文祥(1991-),男,安徽安庆市人,主要从事物理海洋方面的研究。E-mail:wenxiangding2015@163.com

*通讯作者：梁楚进(1966-),男，研究员,主要从事大洋环流与海气相互作用方面的研究。E-mail:cjliang@sio.org.cn

P731

A

1001-909X(2017)01-0014-11

10.3969/j.issn.1001-909X.2017.01.002

丁文祥，梁楚进，廖光洪，等.南极普里兹湾海域湍流扩散系数估计[J].海洋学研究,2017,35(1):14-24,

DING Wen-xiang, LIANG Chu-jin, LIAO Guang-hong, et al. The turbulent diffusivity estimation in Prydz Bay, Antarctic [J].Journal of Marine Sciences,2017,35(1):14-24, doi:10.3969/j.issn.1001-909X.2017.01.002.