三轴地磁传感器校正方法在可穿戴体感设备中的应用
陈法圣 孙宏志 何雅楠 刘静楠


摘要:可穿戴设备中往往会需要测量地磁场来计算设备姿态以提高用户的体验。为了提高磁传感器采集数据的精度,文章提出了一种三轴磁传感器标定方法。该方法通过提出新的损失函数和对数据加权,使得校正后的数据在传感器处于不同姿态下误差更小。在外界磁场存在噪声强度为2.72%的模拟数据上,传统方法在不同姿态误差均值最犬可达到6.59%,而文中方法最大仅为2.9%。
关键字:三轴磁传感器标定;误差校正;可穿戴体感设备
1.三轴地磁传感器研究背景
三轴地磁传感器是可穿戴体感设备中的重要组成部分。其通过测量地磁场矢量,可以计算出设备的姿态。以vR头盔为例,通过计算地磁矢量在水平面上的投影,即可得到无积累误差的水平方向角,使得用户在使用VR设备时不会遇到视角漂移的问题。由于可穿戴设备中的磁传感器均通过电路驱动,其必然会收到所在电路的磁场干扰,所以磁传感器的校正是可穿戴设备研发的重中之重。然而传统的地磁传感器校正方法存在各种各样的问题:首先,其校正方法过于简单,没有考虑校正模型导致的系统误差,使得在视线方向不同时,校正后的误差也不同,影响用户体验;其次,传统方法没有考虑用户在重新标定时所采集的不均匀数据,导致的校正精度下降。因此本文提出了一种新的磁传感器校正系数计算方法来解决这些问题。
三轴磁力计的误差主要分为3种:偏置误差、灵敏度误差。而当传感器所在载体存在恒定磁场时,测得磁场会存在恒定偏置,即偏置误差。而当传感器在磁场校正时各轴对磁场的灵敏度不同,即灵敏度误差。由于环境磁场在无噪声时,可以看作恒定磁场,所以,只要能拟合出椭球方程,计算出椭球的中心和各轴的长度,即可把椭球还原为正球,完成标定、校正的工作。
磁力计标定方法主要分为自标定与非自标定两类。非自标定法需要外部设备采集磁力计在各读数下的姿态,虽然精度高但不易实现;而自标定法无需其他外设,常用于可穿戴设备。大多数磁力计自校准方法都基于最小二乘椭球方程拟合。该类方法通过采集数据拟合椭球方程,来计算出传感器的标定参数。在计算精度/实时性等方面,许多论文都进行了改进。
4.实验及分析
4.1实验及结果
为了验证本文方法的正确性,笔者通过计算机模拟的方法进行试验与分析。
先构造数据分布不均匀的无误差数据,各项误差(偏置误差、灵敏度误差、观测误差)与观测数据(有误差数据)。构造出的观测数据如图1所示。利用观测数据,分别使用传统的最小二乘椭球方程拟合法与本文方法,计算标定系数。之后按照经纬度,离散出多个方向,在每个方向上模拟采样,分别计算两种方法的绝对误差的平均值与方差。在单位球上,按照经纬度,如图2所示,共选取了441个方向,在每个方向上,模拟1万份数据,用以计算校正后相对误差的均值与方差均值,其中蓝色的箭头指向的方向表示选取的方向。
如图3所示,左边为最小二乘椭球方程拟合法在各个方向上的绝对误差平均值分布图,右边为本文方法绝对误差平均值分布图。对于球面上的某一点来说,原点到该点的方向向量表示校正后外界磁场矢量的方向;点的颜色表示在该方向上,绝对误差平均值的大小,颜色与大小的关系参照右边的色标。可以看出,对于本文方法在各个方向上绝对误差的均值基本相同,传统类的方法在不同方向上绝对误差的均值不同,南北极处的误差很大。本文方法各项误差更小
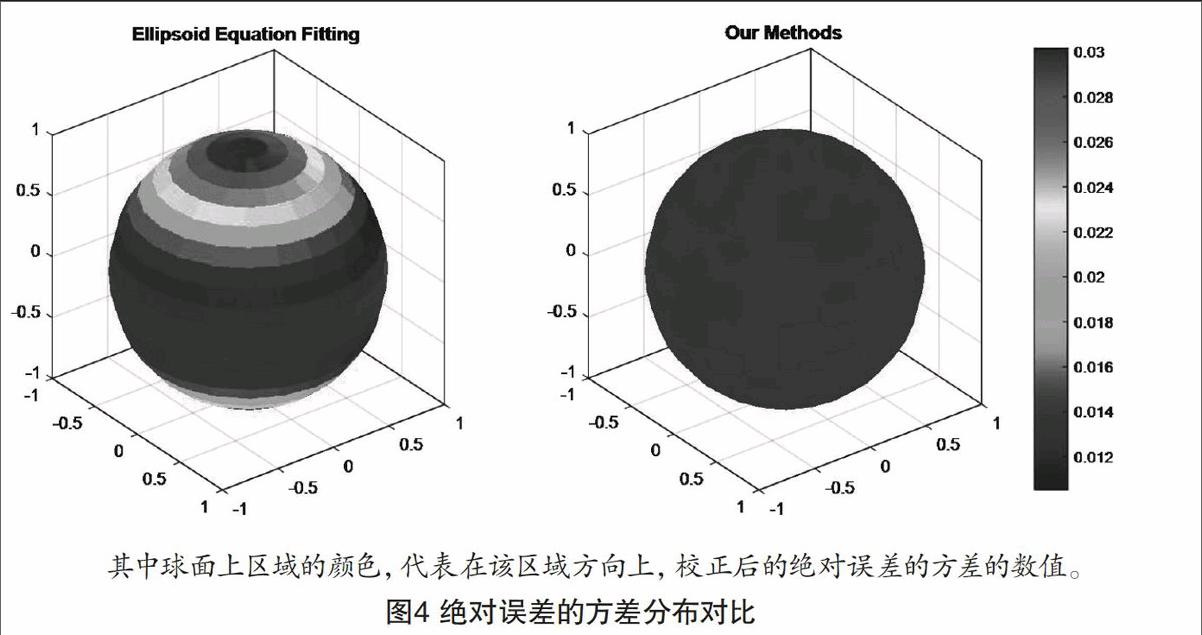
除此之外,笔者还分析了两方法在各个方向上绝对误差的方差。如图4所示,对于球面上的某一点来说,原点到该点的方向向量表示校正后外界磁场的方向;点的颜色表示在该方向上,绝对误差方差的大小,颜色与方差大小的关系参照右边的色标。可以看出,本文方法誤差扰动更小。
4.2分析
本文提出的新的损失函数与加权的方法,是解决当数据分布不均匀且环境磁场存在噪声时各向误差分布不均匀问题的关键。
新的损失函数使得在优化的过程中,x,y,z轴方向上有相同形式的约束项。传统拟合椭圆方程的方法目标函数I,(θ)虽然在交换x与y后,函数的形式仍然没有变化,在轴与y轴方向上有相同约束,但是当交换x与z或y与z后,函数的项发生了变换,所以这种约束函数在z方向上的约束与x、y方向上的约束是不同的。这就导致了在选取方向在z轴分量上变化时,J(θ)约束不同,误差不同。而对于本文提出的_,(W)而言,无论如何交换x,y,z的顺序J(w)的各项没有变化,所以具有在各方向上约束相同的特性。故如图4左边所示,相对于传统方法,本文在各个方向上,误差的分布较传统方法更小且更为均匀。
而在损失函数加j(w)入的权重,是使得各向误差分布均匀的另一个关键因素。权重入i使得密集区域的数据点权重低一些,稀疏区域的点权重大一些,平衡数据分布不均匀导致的各向误差差异。
通过本文提出的这两个新策略,使得部署在可穿戴便携设备上的地磁传感器无论处在任何姿态下,误差分布相同,便于后续滤波器的设计。而且相比于椭球校正法,在保证使用标定参数的时候时间空间复杂度不变且提高了算法的精度。最后,本文提出的方法考虑到了用户在重新校正时经常发生的采集数据分布的问题,提高了算法的鲁棒性,非常具有工程应用价值。

