太阳能光伏板风荷载分布模型试验研究

马文勇， 孙高健， 刘小兵， 邢克勇， 刘庆宽

(1.河北省大型结构健康诊断与控制实验室，石家庄 050043； 2.石家庄铁道大学 土木工程学院，石家庄 050043；3.河北省电力勘测设计研究院，石家庄 050043)

太阳能光伏板风荷载分布模型试验研究

马文勇1,2， 孙高健2， 刘小兵1,2， 邢克勇3， 刘庆宽1,2

(1.河北省大型结构健康诊断与控制实验室，石家庄 050043； 2.石家庄铁道大学 土木工程学院，石家庄 050043；3.河北省电力勘测设计研究院，石家庄 050043)

引起太阳能光伏板及其支架风致损坏的一个主要原因是其抗风设计方法尤其是风荷载取值模型仍不够完善。通过刚性模型测压风洞试验得到的光伏板表面体型系数分布规律及其产生的整体风荷载，提出了考虑光伏板倾角及风致弯矩影响的四角点平面风荷载分布模型及偏心距模型。结合光伏板的结构特点，给出了均匀分布、梯形分布和偏心距三种用于抗风设计的风荷载取值模型。该研究分析了目前风荷载取值模型的不足并提出了改进措施，通过三种风荷载分布模型的对比，为光伏板抗风设计的风荷载取值提供了依据。

光伏板；风洞试验；体型系数；风荷载模型

支持和鼓励企业、机构、社区和家庭安装、使用光伏发电系统是解决目前我国面临能源和环境压力主要方案之一。这些大量出现的分布式光伏板及其支架常常在强风的作用下发生破坏。其中一个重要的原因是由于针对光伏支架这种小型结构，其主要风荷载是作用在光伏板表面上的风压，在其大面积应用前，针对其风荷载研究相对缺乏，抗风设计方法及风荷载取值模型都不完善。

按照我国《建筑结构荷载规范》[1]中的规定，结构风荷载的主要参数采用体型系数描述。该规范中并未规定光伏板结构的体型系数，但可以参考开敞单坡顶盖屋面体型系数取值。我国《光伏发电站设计规范》[2]中对光伏板体型系数的取值规定“地面和楼顶支架的体型系数取1.3”。针对目前的光伏支架设计，以上规定无论对光伏支架风荷载随倾角变化以及风荷载分布形式上都有待完善。美国土木工程协会(The American Society of Civil Engineers， ASCE)[3]规定底部开口建筑屋盖的风荷载与我国《建筑结构荷载规范》类似，其考虑了倾角对风荷载的影响，迎风端和背风端的取值不同。欧洲规范[4]将开敞单坡顶盖风荷载分为九个区域并且考虑了屋盖倾角以及底部阻塞率对表面风荷载的影响。日本太阳能光伏发电系统的设计与施工[5]中，给出了地面单独安装和屋顶安装时风力系数取值，并且给出了风力系数随倾角的变化。

以上的五个设计标准对光伏板风荷载分布模型及取值存在较大差异：从风荷载分布形式上，分别出现了均匀分布、两区域均匀分布和九区域均匀分布；从倾角影响看，我国《光伏发电站设计规范》不考虑倾角影响，其针对平行地面安装的光伏板正压体型系取值是欧洲规范对应值的7倍。

张庆祝等[6]通过风洞试验测试认为必须考虑风荷载作用在光伏板上偏心形成的弯矩。贺广陵等[7]也提到了考虑风荷载引起光伏板弯矩的重要性，并认为采用梯形分布可能更合理。文献[8-11]关注了屋顶上太阳能光伏板的风荷载分布问题。

从以上的相关研究成果可以看出，光伏板表面风荷载的分布形式和不同倾角下的光伏板的风荷载取值是目前光伏板风荷载取值模型存在的主要问题。本文通过刚性模型测压风洞试验，获得光伏板表面的风荷载分布，通过对其产生的整体风荷载分析，提出了考虑风荷载分布及倾角影响的梯形分布模型和偏心距模型，为光伏板的抗风设计提供了建议和依据。

1 模型及试验介绍

试验在石家庄铁道大学风洞实验室低速试验段进行[12]，试验段4.4 m宽，3 m高，24 m长。该试验段在23 m/s风速下，速度场不均匀性<1%，背景湍流度<1%。此次试验为刚性模型测压试验。

1.1 模型简介

太阳能光伏板有多种规格。图 1中光伏板长度L=3 280 mm；光伏板宽度B=1 984 mm；光伏板厚度为50 mm；光伏板离地高度H=0.5 m。试验中采用4∶1的试验缩尺比。为方便调节，光伏板采用四个高度可调的边长为20 mm的方柱支撑，该尺寸主要是从模型制作和调整的角度考虑，与实际光伏板支撑有一定的差别。模型采用ABS板制作，模型上下表面对应的120个位置布置有测压点，共240个测压点。

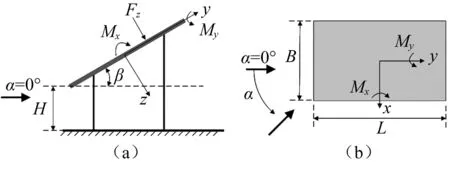
图1 模型及试验参数定义Fig.1 Test model and definition of testing parameter

1.2 试验概况

试验采用低湍流度均匀流场(湍流度1%左右)自由来流风速为12 m/s。压力测试采用ESP-64Hd压力扫描阀配合DTC采样系统，该系统的测试精度为满量程(2 540 Pa)的0.1%。采样频率为331.6 Hz，采样时间为30 s。测压管长度为1.2 m，采用分布摩擦理论模型进行了管路信号畸变修正。

图 1中：α为风向角，取值为0°～180°，以15°为间隔；β为光伏板倾角，分别取5°、10°、20°、30°、40°、55°六种工况。

1.3 参数定义

定义测点的体型系数为

(1)

式中：μsi(t)为i点体型系数；Pwi(t)和Pni(t)为i点位置的光伏板上表面风压和下表面风压；U为来流风速。整体体型系数μs、绕短轴和长轴的弯矩系数CMx和CMy分别定义为

(2)

式中：Ai为i点代表的面积；yi和xi为i点的坐标值。

2 光伏板风荷载分布模型

由于目前各个区域的设计规范中对光伏板表面的风荷载分布形式仍存在较大的差异，本节讨论光伏板表面的体型系数分布及其模型。该模型需要反映作用在光伏板上的整体风荷载，同时也要兼顾光伏板表面风荷载的分布规律。

2.1 光伏板体型系数分布规律

图 2给出了倾角为β=30°光伏板在风向角α=0°、α=180°、α=30°和α=150°的体型系数分布规律。当α=0°时，从分布上来看，体型系数沿光伏板长轴方向(顺风向)表现出明显的梯度，光伏板顶端的体型系数为0.4左右，而底端(迎风端)的体型系数达到1.8左右；当α=180°时，光伏板底端的体型系数为-0.4，而顶端(迎风端)的体型系数达到-2.2。对于控制风荷载常发生的α=0°和α=180°风向角，这种体型系数分布将会产生明显的弯矩，因此均匀分布的风荷载模型无法描述这类风荷载。对于α=180°，体型系数沿着光伏板的短轴方向也存在一定变化，这种变化主要是由于气流绕光伏板两侧及两端的三维分离造成的。

当光伏板处于斜风向下时，以α=30°和α=150°为例，其风压分布仍表现出一定程度沿顺风向的梯度，这种梯度不仅形成绕光伏板短轴的弯矩，也产生了绕光伏板长轴的弯矩。另外从分布形态上看，已有的均匀分布、两区域均匀分布都无法描述各个风向角下的风压分布，但是对于倾角较大(α>20°)的光伏板而言，其最大整体体型系数发生在α=0°和α=180°风向角下。在该风向角下，风压分布的规律性明显，因此从抗风设计的角度看，采用简化的分布模型是可行的。

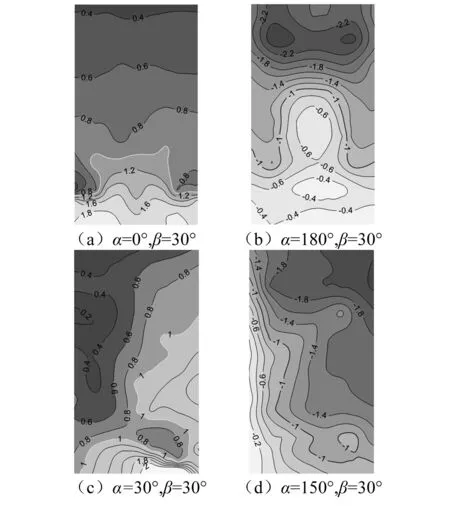
图2 光伏板表面体型系数分布Fig.2 Shape coefficients distribution on solar panel

2.2 光伏支架的整体风荷载

一般来说，作用在光伏板上的风荷载通过光伏板表面传递给光伏支架，其风效应主要体现为垂直于板面的z向力Fz, 绕光伏板短轴的弯矩Mx和绕光伏板长轴的弯矩My(见图 1)。此处采用整体体型系数μs描述垂直于板面的风荷载，用弯矩系数CMx和CMy描述作用在光伏板上风荷载产生的弯矩。

图 3给出了作用在不同倾角光伏板表面的不同风向角下的整体风荷载等值线图。图 3(a)的整体体型系数分布图可以看出，正压体型系数在α=0°左右取得最大值，倾角越大，正压体型系数越大，在测试倾角范围内，其最大值达到1.3左右，这与我国《光伏发电站设计规范》的规定是吻合的。与≥30°倾角的光伏板不同，倾角<30°的光伏板，其最强负压体型系数并未发生在180°风向角下，并且各个倾角光伏板随着倾角的增大，其最强负压体型系数并未单调增强，其最强值发生在45°倾角左右，整体体型系数达到-1.6左右，该值比我国《建筑结构荷载规范》和《光伏发电站设计规范》的取值都要大。另外，从等值线的延伸规律来看，风向角为90°时，体型系数并非为0。其主要的原因是由于实际光伏板或者试验光伏板有一定的厚度，并非理想平面，这种厚度的造成流体分离对光伏板表面风荷载的影响，在风向与光伏板倾斜方向平行工况附近很小(即最强体型系数对应的工况)，同时对于较大的倾角的光伏板影响很小(即风荷载比较大的工况)。

由于光伏板表面风荷载分布不均匀形成了绕光伏板短轴(见图 3(b))和长轴的弯矩(见图 3(c))，其弯矩系数分别为CMx和CMy。为方便辨认弯矩系数较大区域，图 3中用粗实线标示出了弯矩系数为±0.05的等值线。绕短轴的弯矩在多数工况下是负值，说明其在光伏板上施加了一个掀翻光伏板的弯矩，该弯矩最强值发生在倾角β=40°，风向角α=180°时，其值达到-0.21。从分布上来看，绕短轴方向的弯矩最大值与整体体型系数的最大值发生工况一致。相比绕短轴的弯矩系数，饶长轴的弯矩系数小一些，其最强弯矩系数约为±0.1，发生的风向角α=45°和α=135°左右。从弯矩系数的分布上来看：绕短轴的弯矩系数CMx发生的工况与最强整体体型系数发生的工况接近且与相关文献中的设计考虑工况接近；绕长轴的较强弯矩均发生在斜风向下，对应的整体体型系数稍小。

通过对整体体型系数和弯矩系数的分析，由于不同风向角下、不同倾角光伏板上风压分布的不均匀，作用在光伏板上的弯矩也随之变化，这种弯矩对于光伏板支架的设计有重要意义，其会增加单柱支撑的偏心距或者多柱支撑的荷载分配。因此需要一种相对简单的可以考虑不同倾角和风向角下弯矩影响的风荷载取值模型。

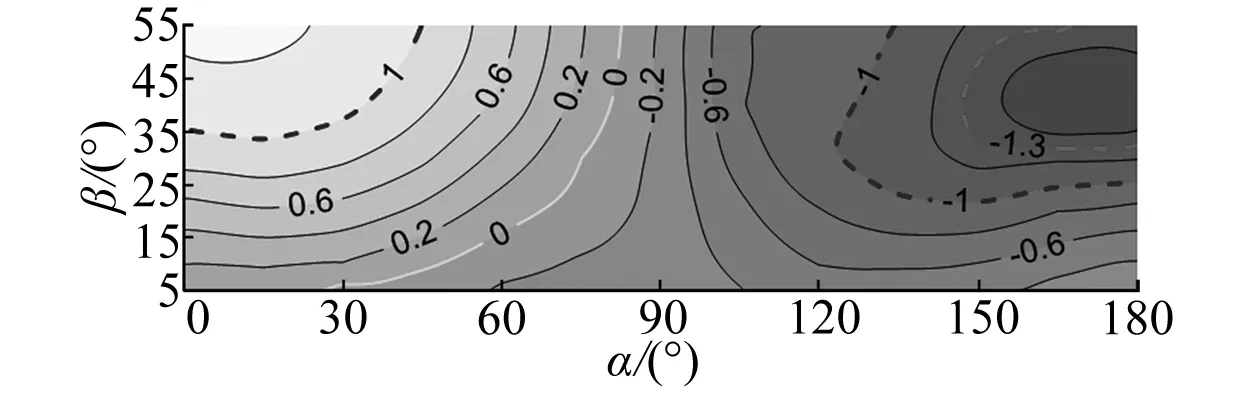
(a) 整体体型系数μs

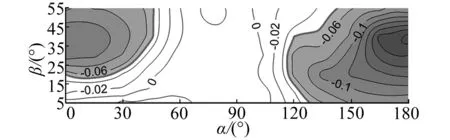
(b) 绕短轴的弯矩系数CMx

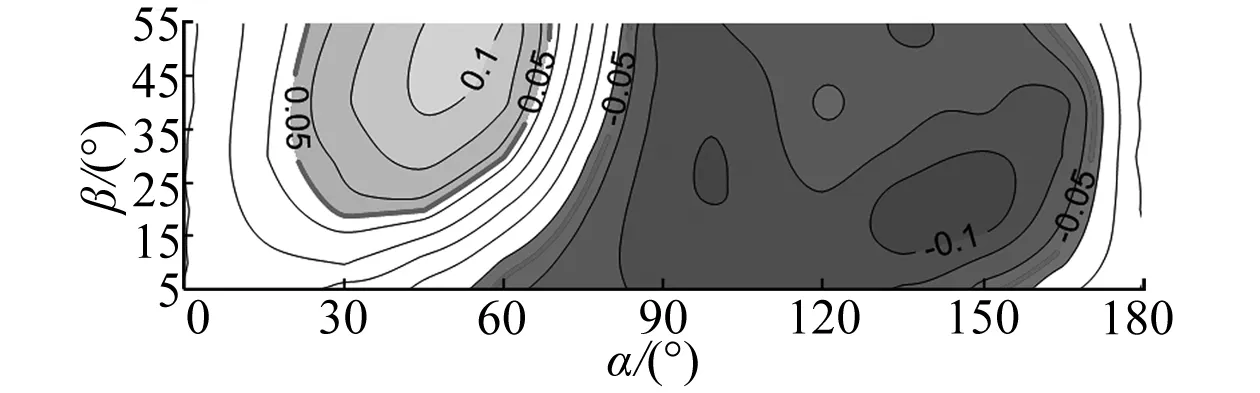
(c) 绕长轴的弯矩系数CMy

2.3 考虑弯矩影响的风荷载分布模型

《光伏发电站设计规范》中采用的均匀荷载分布模型无法反映作用在光伏板上的弯矩。《建筑结构荷载规范》中的两区域取值可考虑绕短轴的弯矩，但无法考虑绕长轴的弯矩，且该模型中体型系数在光伏板中间突变与实际分布差别很大。虽然九区域均匀分布模型从理论上可以考虑各个方向的弯矩，但是针对光伏支架设计而言，将其表面划分为9个区域并分别取值非常麻烦。本节讨论四角点平面分布风荷载和偏心风荷载两种分布模型。

四角点平面分布风荷载模型(见图 4)假设作用在光伏板表面的风压为一平面分布，因此光伏板四个角点的体型系数分别为μA、μB、μC和μD应满足平面协调条件、Fz、My和Mx三个方向力的等效四个条件。

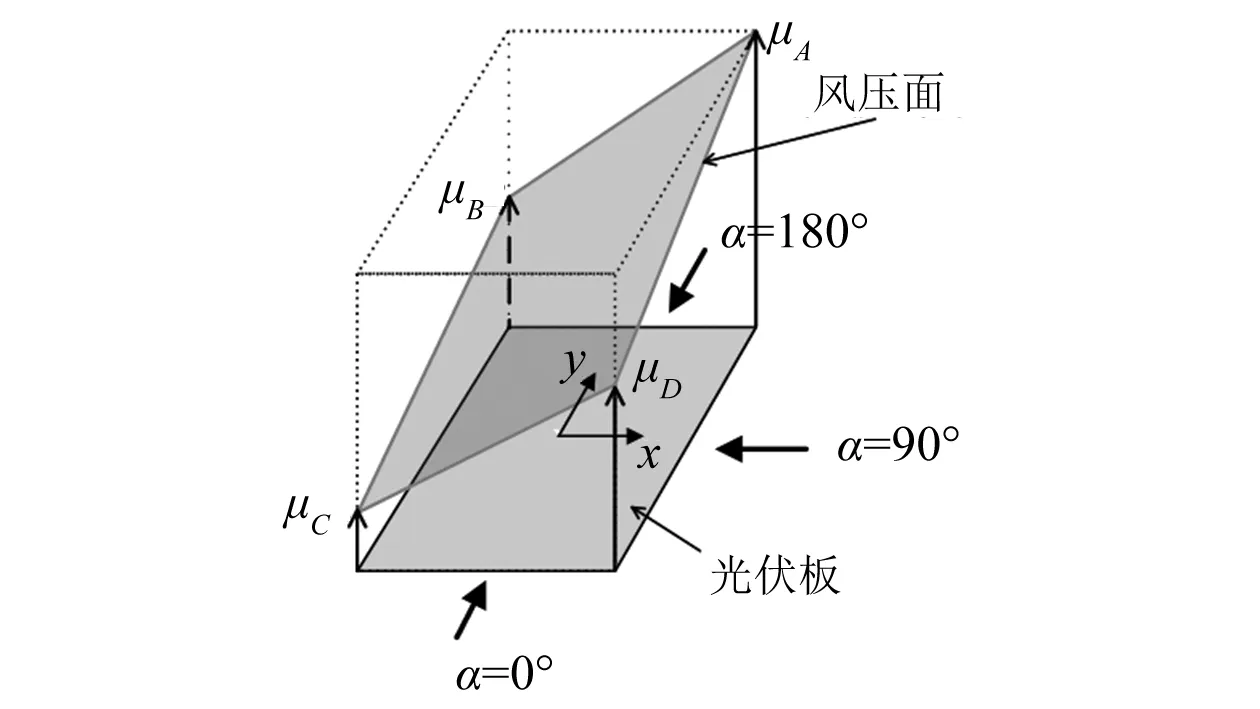
图4 光伏板平面风荷载分布模型示意图Fig.4 Scheme of four-corner-distribution wind load model

式(3)为四个角点体型系数的数学表达式，通过求解该方程，可得到满足整体风荷载等效条件的四个角点的体型系数。

(3)

以倾角β=30°光伏板为例，求解式(3)得到的四角点体型系数与整体体型系数及弯矩系数的对比见图 5。其中左侧纵坐标μ表示体型系数，右侧纵坐标CM表示弯矩系数。计算得到的四个角点的体型系数差别取决于弯矩的大小，当α=180°时，绕长轴方向的弯矩系数CMy接近于0，因此μA与μB值接近、μC和μD值接近。此时绕短轴方向的弯矩系数CMx达到-0.18，μA与μC取值差别很大。对比图 6中四角点的体型系数取值与图 5中实际测试得到的体型系数取值可知，计算得到的四角点体型系数虽然与测试得到的体型系数值不同，但是其反映的风压分布规律与测试结果是一致的。

对于整体体型系数最大的α=0°和α=180°两个风向角下，图 6给出了四角点体型系数中，不同倾角光伏板迎风端两侧体型系数及背风端两侧体型系数的对比，其中图例落在实线上，说明横坐标与纵坐标代表的体型系数值一致。如α=0°，迎风端两侧的体型系数μC和μD值非常接近，同时背风端两侧体型系数μA和μB值也相同。这说明各个倾角的光伏板，其α=0°和α=180°的体型系数可以采用梯形分布，也说明贺广陵等提出的梯形分布是合理的。由于绕短轴的弯矩相比绕长轴的弯矩更大，且其在较大倾角光伏板上与最强整体体型系数发生的工况一致。因此对于大部分光伏板设计，采用梯形分布模型不仅可以有效的描述光伏支架的风荷载取值，也可以近似描述光伏板表面的体型系数分布。

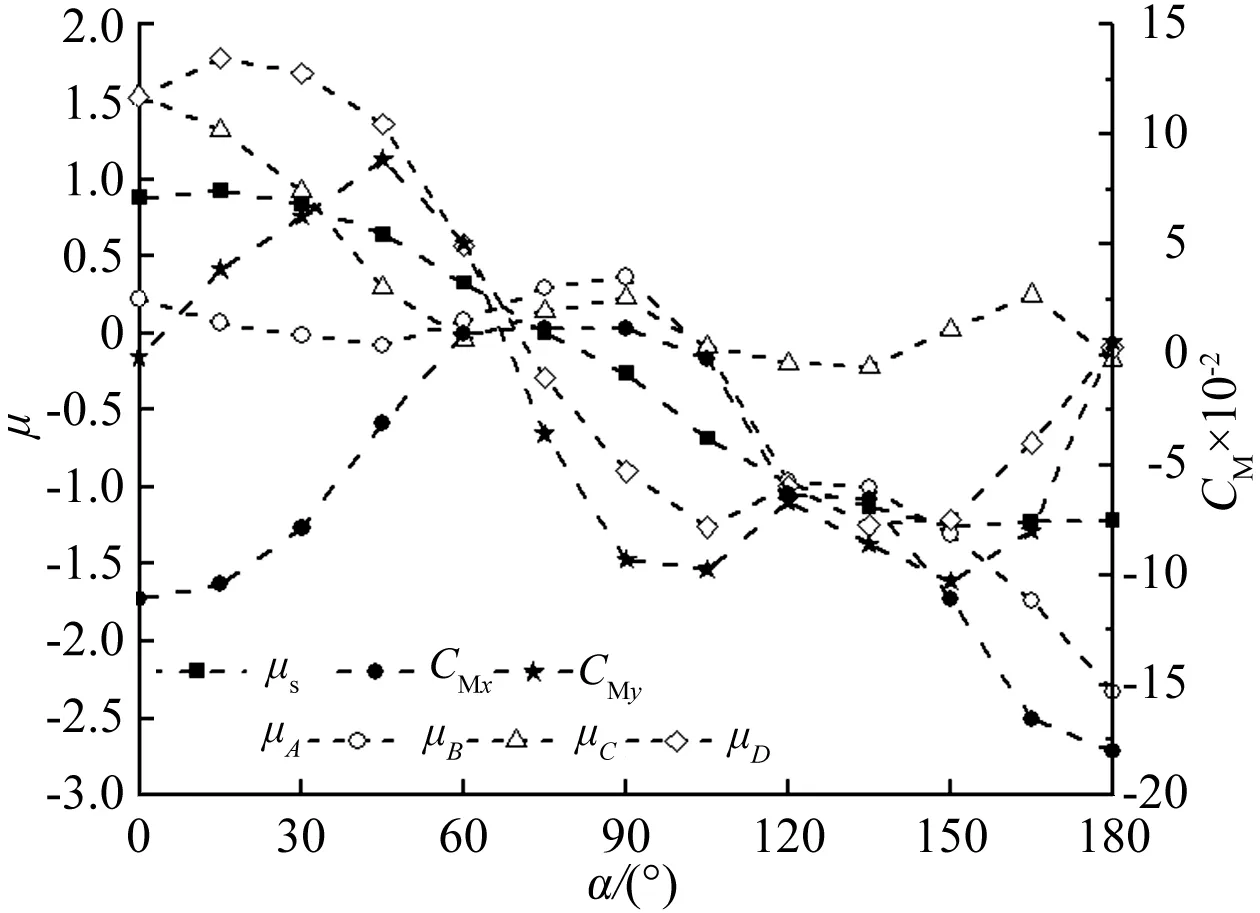
图5 四角点平面分布体型系数取值对比Fig.5 Comparison of shape coefficients on four corners

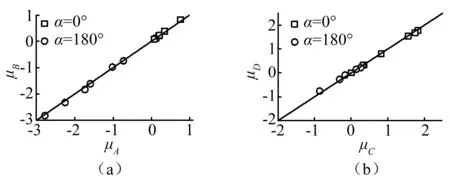
图6 梯形风压分布的验证Fig.6 Validation of trapezoidal distribution model

另一种考虑弯矩的风荷载分布模型是偏心风荷载分布模型。即采用整体体型系数的方式考虑垂直于光伏板表面的荷载，采用偏心距考虑风压不均匀分布形成的弯矩。这种模型无法考虑光伏板表面的体型系数分布，可以用更直接的方式给出光伏支架的整体风荷载。其长短轴方向的偏心距分别定义为

(4)

图 7为光伏板在α=0°和α=180°风向角下的绕短轴的偏心距随光伏板倾角变化的规律。从规律上来看，当α=180°时，倾角越大的光伏板，其弯矩较大，偏心距却较小，这说明，随着倾角的增大，整体体型系数的增加快于弯矩系数的增大。图7中β=5°倾角的偏心距数据与其他倾角光伏板的差异较大，其主要是由于其整体体型系数较小，可能存在较大的计算误差。当α=0°时，绕短轴的偏心距随倾角增大变化不大。

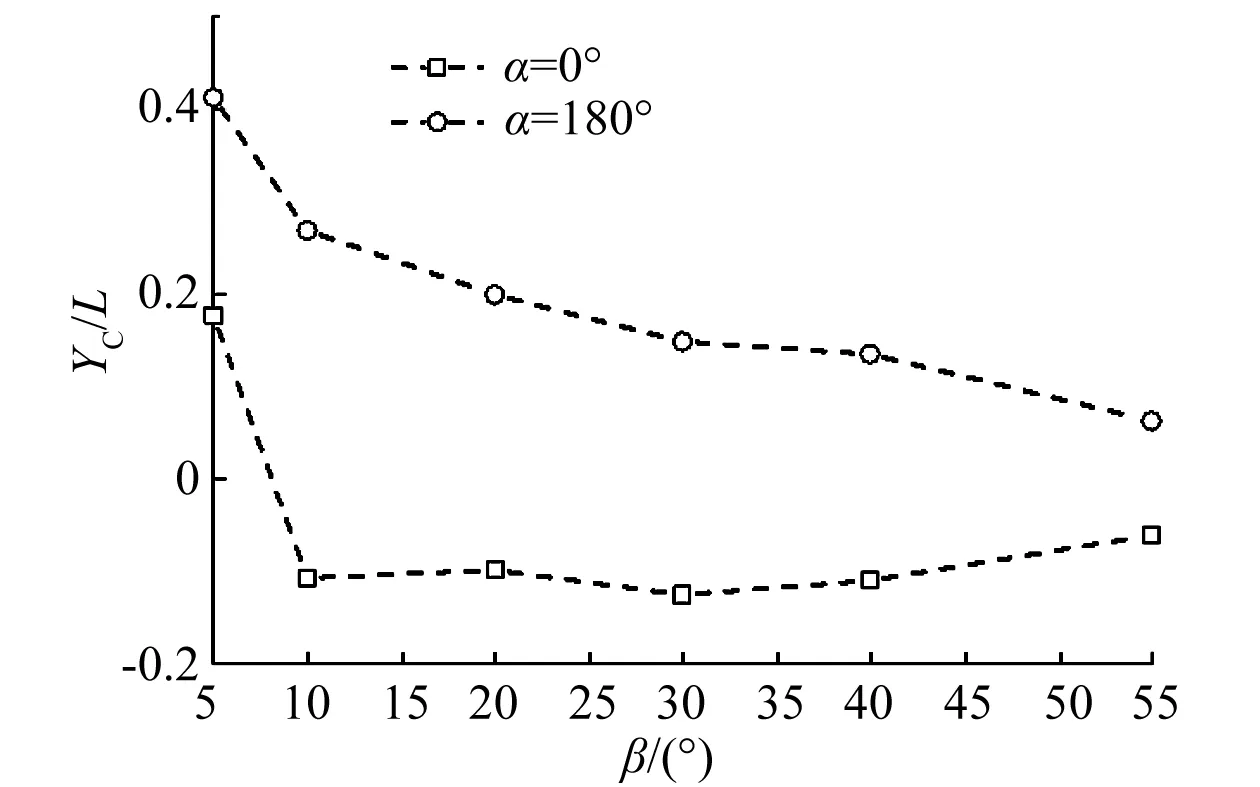
图7 绕短轴偏心距随倾角变化Fig.7 Variation of eccentric distance in length with the inclination

3 光伏板风荷载取值建议

通过以上对光伏板风荷载整体风荷载及其分布模型的分析，针对光伏板抗风设计的不同需求，其体型系数的取值可以采用均匀分布、梯形分布和偏心距模型三种分布模型。值得说明的是，虽然在某些倾角的最强风荷载并未发生在α=0°和α=180°风向角下，考虑到使用的方便性，本节风荷载取值建议中统一将该倾角下最强正压风荷载作为α=0°的风荷载，将最强负压风荷载作为α=180°风荷载，即表1～表3的风荷载是该倾角光伏板的最不利值，但其并非一定发生在α=0°和α=180°风向角下。

3.1 均匀分布风荷载模型及其取值

对于不考虑风荷载引起弯矩影响的情况下，均匀分布模型采用均匀分布的体型系数。这种取值模型简单，与目前我国《建筑结构荷载规范》和《光伏发电站设计规范》的取值方法有很好的统一性，并在以上两个规范的基础上增加了倾角对光伏板体型系数的影响，解决了上述规范对小倾角光伏板体型系数取值偏于保守，对大倾角光伏板体型系数取值偏于危险的问题。其具体的取值见表 1。其中为了与现有规范统一，参数定义见表 1中的示意图。

3.2 梯形分布风荷载模型及其取值

梯形分布模型是本文提出的四角点平面分布风荷载分布模型的简化形式。相比于均匀分布，梯形分布模型不仅考虑了绕短轴的弯矩影响，同时也给出了近似的风荷载分布规律。虽然该模型无法考虑绕长轴的弯矩影响，但是由于绕短轴的弯矩值大于绕长轴的弯矩值，本文测试的绕短轴最大弯矩值Mx(发生在β=0°，α=180°)是绕长轴最大弯矩值My(发生在β=20°，α=150°)的2.88倍。因此对于多数光伏板支架而言，这种考虑绕短轴弯矩影响的梯形分布满足其体型系数取值要求。其具体取值见表 2。

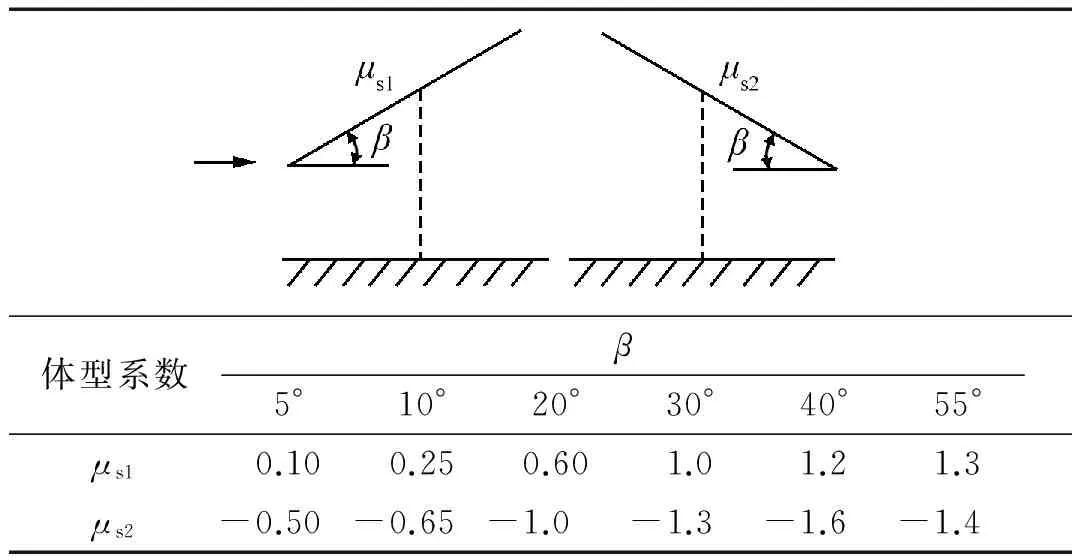
表1 均匀分布风荷载模型及其取值

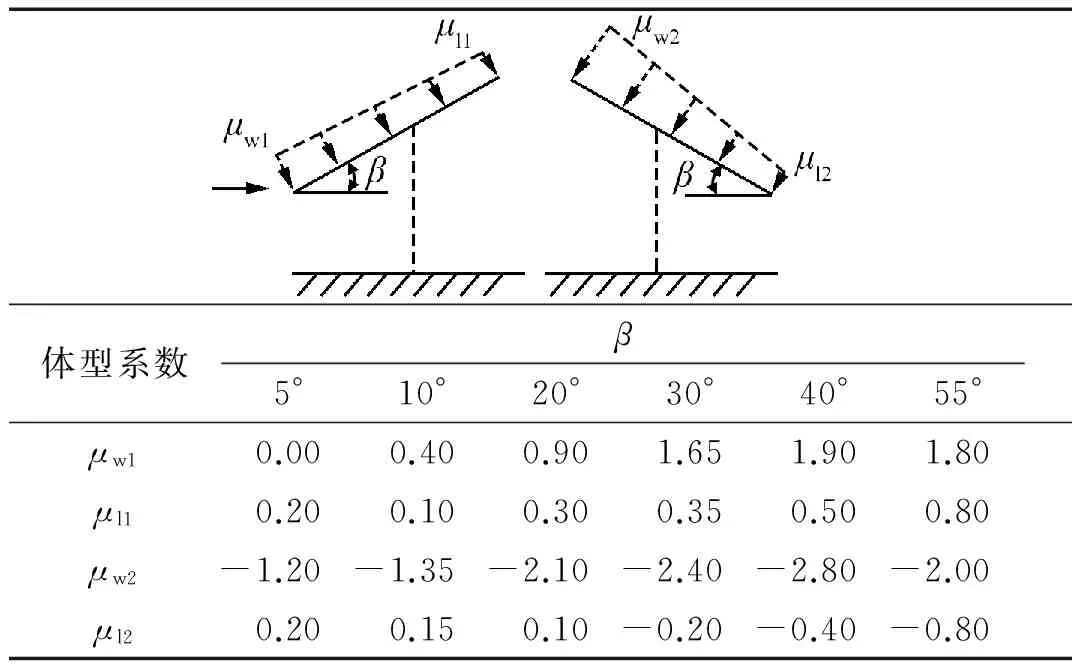
表2 梯形分布风荷载模型及其取值

3.3 风荷载偏心距模型及其取值

虽然梯形分布模型可以满足大部分光伏板的体型系数取值要求，考虑到光伏板支架形式的多样性，部分支撑形式下绕长轴的弯矩会有较大影响，因此本节给出风荷载偏心距模型。该模型是对均匀分布模型的补充和深化。表 3给出了偏心距模型及其取值，由于实际测试中绕短轴和绕长轴的弯矩发生在不同的风向角下，因此光伏板风荷载可按照单向偏心考虑，即表 3中的XC和YC不同时考虑。需要进一步说明的是：表 3中的偏心距并不针对某个具体的风向角，该偏心距是根据最强整体体型系数与最大弯矩计算得到的，这种方法可以保证表 3中的荷载包含了结构承受的最不利风荷载，但是在绕长轴的弯矩取值方面，由于实际最大弯矩对应的整体体型系数与最强整体体型系数有一定的差异，因此该取值方法会比实际值保守。

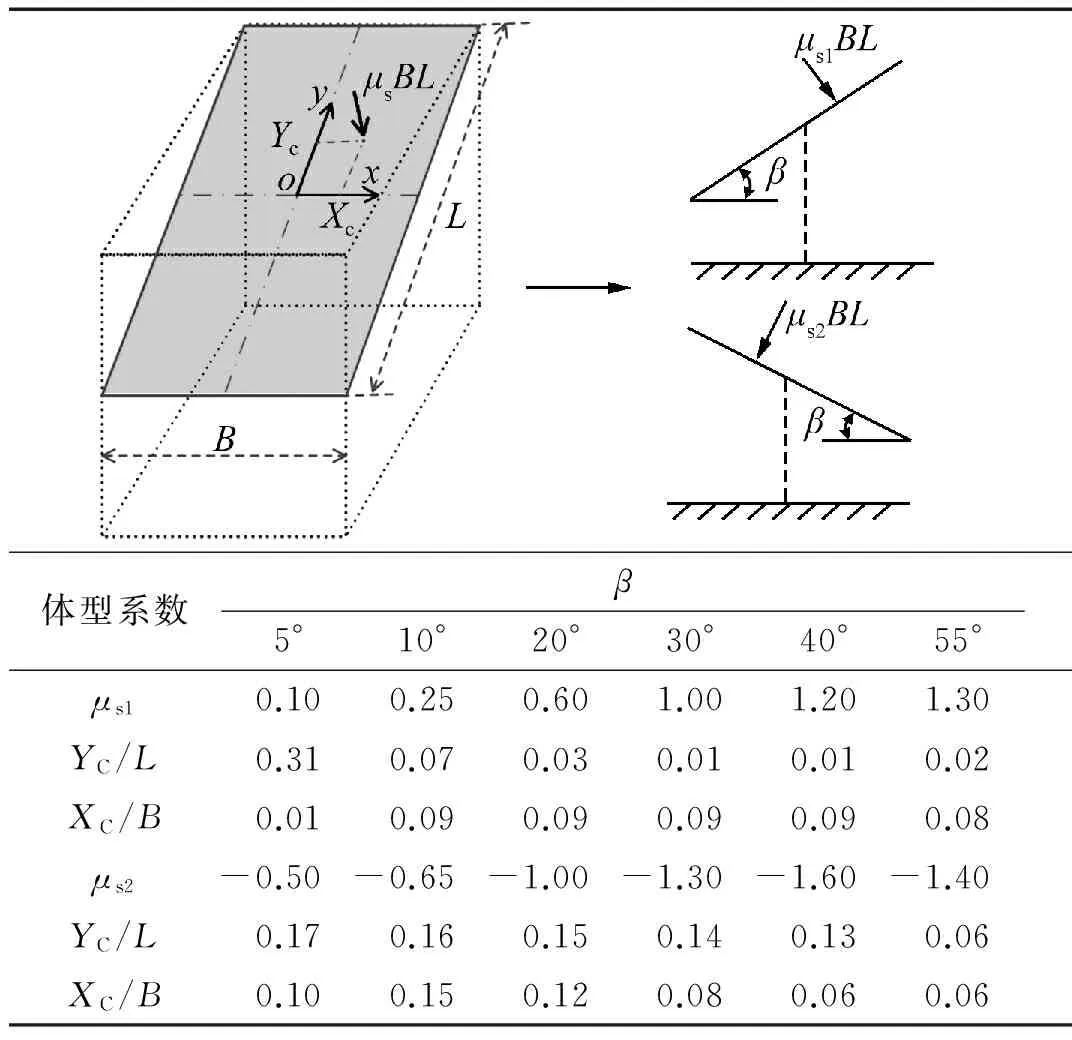
表3 偏心距模型及其取值

4 结 论

通过刚性模型测压风洞试验，本文提出了四角点平面风荷载分布模型和偏心距模型，并根据光伏板的结构特点，给出了均匀分布模型、梯形分布模型和偏心距模型及其风荷载取值。得到如下结论：

(1) 目前我国《光伏发电站设计规范》中的体型系数取值，对于倾角<30°的光伏板体型系数取值偏于保守，对于倾角>30°的光伏板体型系数取值偏于危险。光伏板的体型系数取值应考虑光伏板倾角的影响。

(2) 由于光伏板表面的风压不均匀分布，作用在光伏板的风荷载表现为垂直于光伏板面的压力以及绕光伏板长轴和短轴的弯矩，其弯矩取值随风向角和光伏板倾角变化，需要引起抗风设计的注意。

(3) 根据不同设计需求，光伏板表面的体型系数分布可采用均匀分布模型、梯形分布模型和偏心距分布模型。其中，梯形分布模型考虑了垂直板面的风荷载及其引起的绕短轴方向的弯矩，并且给出了体型系数的近似分布形态，可以满足大部分光伏板风荷载的取值要求。对于诸如光伏板底部支撑布置严重对称等特殊情况，需要考虑双向弯矩时，可采用偏心距模型分别对两个方向进行计算。

本文提出的梯形分布和偏心距两种考虑弯矩的取值模型需要通过不同支撑类型的光伏板设计检验，才能确定哪种模型更适合目前我国光伏板抗风设计。另外本研究针对的是单个光伏板，多块光伏板组成的光伏板组，需要进一步研究确定其具体的风荷载取值参数。

[ 1 ] 建筑结构荷载规范：GB 50009—2012[S]. 北京：中国建筑工业出版社，2012.

[ 2 ] 光伏发电站设计规范：GB 50797—2012[S]. 北京: 中国计划出版社，2011.

[ 3 ] Minimum design loads for buildings and other structures：ASCE/SE 7-10 [S] . American Society of Civil Engineers，2013.

[ 4 ] Eurocode 1: actions on structures, Part 1-4: general actions-wind actions ：prEN 1991-1-4 [S]. Brussels: European Committee for Standardization, 2004.

[ 5 ] 太阳光发电协会(日本). 太阳能光伏发电系统的设计与施工 [M]. 北京: 科学出版社, 2006.

[ 6 ] 张庆祝, 刘志璋, 齐晓慧, 等, 太阳能光伏板风载的载荷分析 [J]. 能源技术, 2010, 31(2): 93-95. ZHANG Qingzhu, LIU Zhizhang, QI Xiaohui, et al. Solar photovoltaic panels wind load testing and analysis [J]. Energy Technology, 2010, 31(2): 93-95.

[ 7 ] 贺广零, 蒋华庆, 单建东, 等. 光伏方阵风荷载模型研究 [J]. 电力建设, 2012, 33(10): 5-8. HE Guangling, JIANG Huaqing, SHAN Jiandong, et al. Research of wind load model in photovoltaic [J]. Electric Power Construction, 2012, 33(10): 5-8.

[ 8 ] STATHOPOULOS T, ZISIS I, XYPNITOU E. Wind loads on solar collectors: a review [C]∥ Chicago： Structure Congress， 2012.

[ 9 ] GREGORY A K. Wind loads on low profile, tilted, solar arrays placed on large, flat, low-rise building roofs [J]. Journal of Structural Engineering, 2013, 140(2): 1-10.

[10] CAO J, CAO S, TAMURA Y. Wind loading characteristics on roof-mounted solar arrays: comparison, interpretation and generalization [C]∥ In 14th International Conference on Wind Engineering, 2015.

[11] CAO J, YOSHIDA A, SAHA P K, et al. Wind loading characteristics of solar arrays mounted on flat roofs [J]. Journal of Wind Engineering and Industrial Aerodynamic, 2013, 123(4): 214-225.

[12] 刘庆宽. 多功能大气边界层风洞的设计与建设[J]. 实验流体力学, 2011, 25(3): 66-70. LIU Qingkuan. Aerodynamic and structure design of multifunction boundary-layer wind tunnel [J]. Journal of Experiments in Fluid Mechanics, 2011, 25(3):66-70.

Tests for wind load distribution model of solar panels

MA Wenyong1，2, SUN Gaojian2, LIU Xiaobing1,2, XING Keyong3, LIU Qingkuan1,2

(1. The Key Laboratory for Health Monitoring and Control of Large Structures, Shijiazhuang 050043, China;2. Civil Engineering College, Shijiazhuang Tiedao University, Shijiazhuang 050043, China;3. Hebei Electric Power Design & Research Institute, Shijiazhuang 050043, China)

A primary reason for wind induced failure of a solar panel and its support structure is the imperfect method for its wind resistance design, especially, the wind load distribution model. Through a rigid model pressure test in a wind tunnel to obtain the distribution law of shape coefficients of the solar panel surface and the whole wind load on the solar panel, a four-corner-distribution model and an eccentric moment model considering effects of both inclination and wind induced moments were proposed. Three wind load models including uniform distribution model, trapezoidal distribution one and eccentric moment one were given in term of structural features of a solar panel. Deficiencies and improvement measures of wind load models used currently in the solar panel design were analyzed. Through comparing the three wind load models mensioned above, a guidance was provided for correctly choosing wind load in the anti-wind design of solar panels.

solar panel; wind tunnel test; shape coefficients; wind load model

河北省教育厅技术研究项目资助(YQ2014039)

2016-05-26 修改稿收到日期：2016-08-19

马文勇 男，博士，副教授， 1981年生

刘小兵 男，博士，副教授， 1982年生

TU311.3; O351.1

A

10.13465/j.cnki.jvs.2017.07.002