基于EOF的ARGO浮标声速剖面重构

李洪超，赵柯柯，师军良

（黄河水利职业技术学院，河南 开封 475004）

基于EOF的ARGO浮标声速剖面重构

李洪超，赵柯柯，师军良

（黄河水利职业技术学院，河南 开封 475004）

利用EOF可以对不完整的ARGO浮标声速剖面进行重构，得到完整的声速剖面。分析了ARGO浮标声速数据预处理方法和剖面重构方法，探讨了不同深度段剖面数据对重构结果的影响。将EOF方法与内插方法比较，得出EOF方法具有较强的实用性和较高的重构精度的结论。

EOF；ARGO浮标；声速剖面；剖面重构；重构精度

0 引言

声音信号在水中良好的传播特性使得水声成为水下定位、导航、探测等的主要信号。水下GPS定位系统是利用水声信号进行定位的系统。通常，它将水中的声速看成不变量 （即取一区域内声速的平均值作为该区域内的声速值）［1］。实际上，声速在水平方向上和垂直方向上都是变化的。对声速不变的假设使得水下GPS测量结果产生较大的误差。因此，如何准确确定海水声速的大小，是进行水下精密定位的关键。

海水声速测量的传统方法主要有2种［2］：（1）先测量海水的电导率、温度、深度（CTD），再利用海水的经验公式反算声速。（2）直接测量。这2种方法都不可能同时获取大量的声速剖面数据。随着ARGO全球海洋观测网的发展，获取海量声速剖面数据成为可能［3～7］。在ARGO浮标测量过程中，由于各种外部原因或者浮标本身的原因，一些浮标测量的温度、盐度、压剖面数据只有部分是可用的，致使计算得到的声速剖面数据也是部分可用。然而，在实际应用中，往往需要该剖面的完整数据。于是，有学者提出了利用部分ARGO浮标声速剖面数据对整个剖面进行重构的命题。Davis［8］证明：在最小均方差意义下，经验正交函数（Empirical Orthogonal Function，简称EOF）是描述声速剖面最有效的基函数。通常，2～3个这样的基函数就可以精确地表达任一声速剖面。国内一些学者关于海洋声速场EOF的研究进一步证明了应用EOF方法研究海洋声速场的可行性［9～14］。张镇迈［15］等利用有限深度声速数据重构全海深声速剖面，验证了基于EOF方法进行声速剖面重构的可行性。笔者在此基础上，探讨了利用不同深度段的部分声速剖面进行重构的方法，并与内插方法进行了比较，验证EOF方法重构声速剖面的高精度性和应用的简便性。

1 试验数据与重构方法

1．1 试验数据

试验区域为北纬21°～23°，东经123°～126°。试验所用数据为2003～2010年 （其中2005年和2007年没有数据）每年10月份ARGO浮标测量的温度、盐度和压力数据。去除一些不合格（剖面太浅）的剖面数据，本试验共选择了56个剖面。其中，55个剖面作为已知数据，选用1个剖面（22．3°N，124．5°E）用来检测重构精度。试验统一选择剖面的范围为海面至海深1 000 m。在试验区域内，ARGO剖面分布如图1示。图中，“Δ”表示检测浮标。

1．2 ARGO数据预处理

（1）根据公式（1），将ARGO浮标的压强数据转化为深度数据。

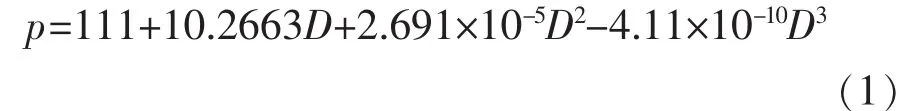
式中：p为压强，kPa；D为水深，m。

（2）利用Medwin经验公式来求解相应的声速剖面，如式（2）所示。

式（2）的适用范围为：0℃≤T≤35℃，0℃≤S≤45‰，0℃≤D≤1 000 m。

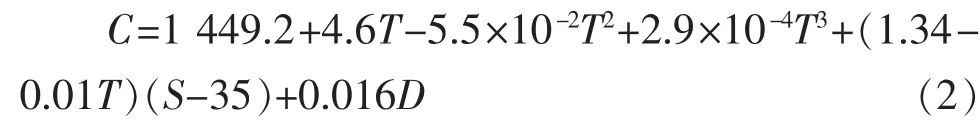
式中：C为声速，m／s；T为温度，℃；S为盐度，1‰。

（3）将计算的声速剖面内插成等间距剖面。实验利用三次样条函数将声速内插成间隔为10m、共100层数据。将内插后的剖面数据当作“实测”的剖面数据。

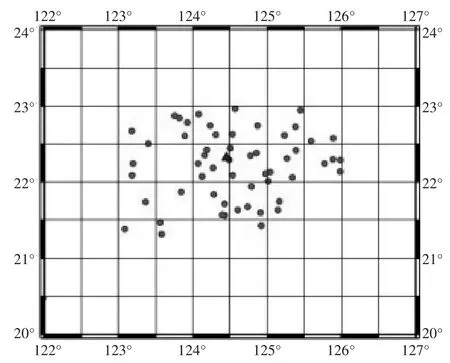
图1 实验海域内浮标分布图Fig.1 Buoy distribution in test sea

1．2 剖面重构方法

假设某区域海水内有N个声速剖面数据，每个剖面由M个离散深度上的声速值组成，则该区域的声速剖面矩阵C如式（3）所示，其协方差矩阵R如式（4）所示。

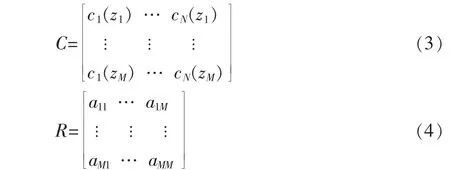
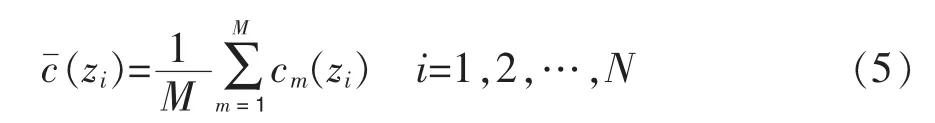
对RMM进行特征值分解，得到式（6）。

式中：ΛMM=为RMM的特征值组成的对角矩阵。

假设λ1＞λ2＞…＞λM，则与特征值相对应的特征向量PMM=PMM的第一列为与λ1相对应的特征向量，以此类推。矩阵PMM即为所求的经验正交函数所对应的矩阵向量。令fk（z）=［ek1ek2… ekM］T，则PMM=［f1（z） f2（z）… fM（z）］。

文献［9］表明，取前几阶经验正交函数就可以较精确地表示实际的声速剖面。如果取前k阶经验正交函数，则区域内任意已知剖面均可表述为式（7）。

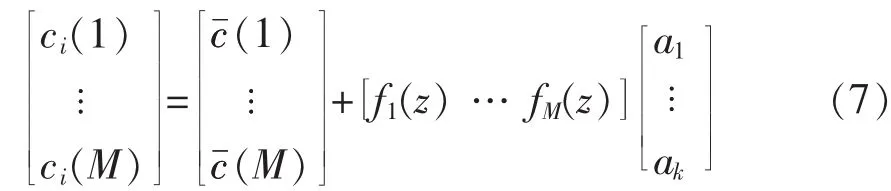
令a=［a1a2… ak］T，可利用区域内部分剖面按式（7）求出系数矩阵a，再将系数矩阵a反代入式（7），即可重构出整个声速剖面。

前k阶经验正交函数对区域的累计贡献率可表示为式（8）［16］。

一般情况下，如果w（k）的值大于或等于90%，利用前k阶经验正交函数就能很好的表示该区域的声速变化。

2 实验结果及分析

2．1 不同深度段数据对重构结果的影响

利用实验区域内55个已知浮标，求得该区域的经验正交函数EOF。为方便表达，仅列出前三阶EOF，如图2所示。

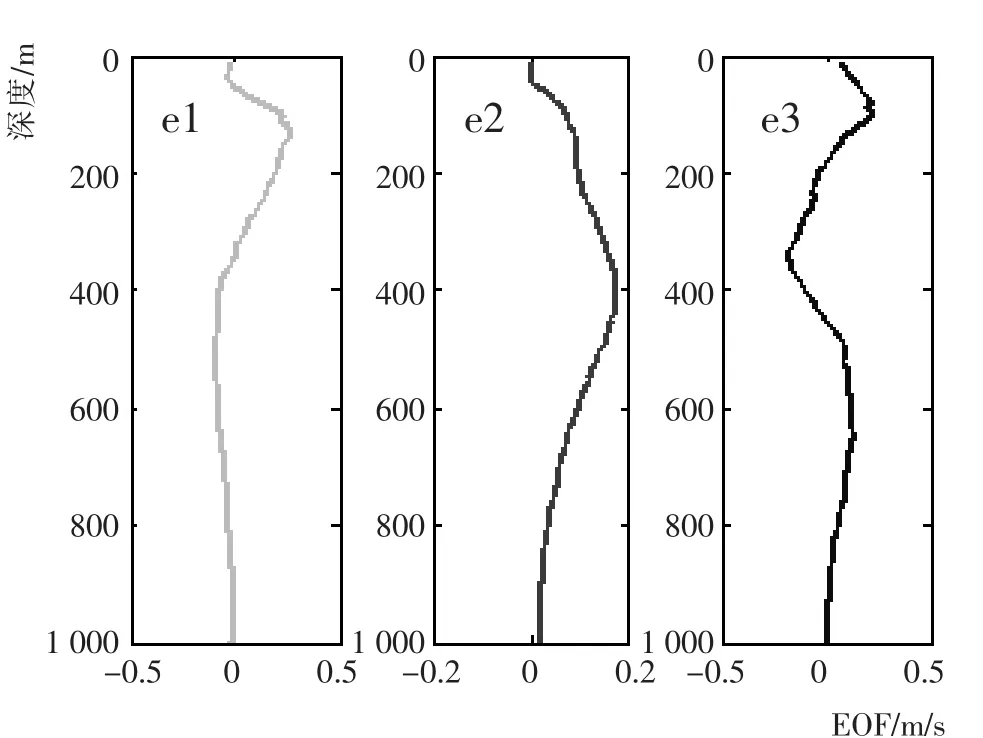
图2 前三阶EOFFig.2 First three order EOF

利用式 （8）计算出前三阶EOF对区域的贡献率，约为96%。因此，利用前三阶EOF对该区域内的声速剖面进行重构，能够得到较好的精度。

分别选取上段（0～300 m）、中段（310～600 m）和下段 （610～900 m）3个剖面数据作为已知部分剖面数据，对位置（22．3°N，124．5°E）处声速剖面进行重构。重构结果如图3所示（实线为实测的声速剖面，虚线为重构的声速剖面）。

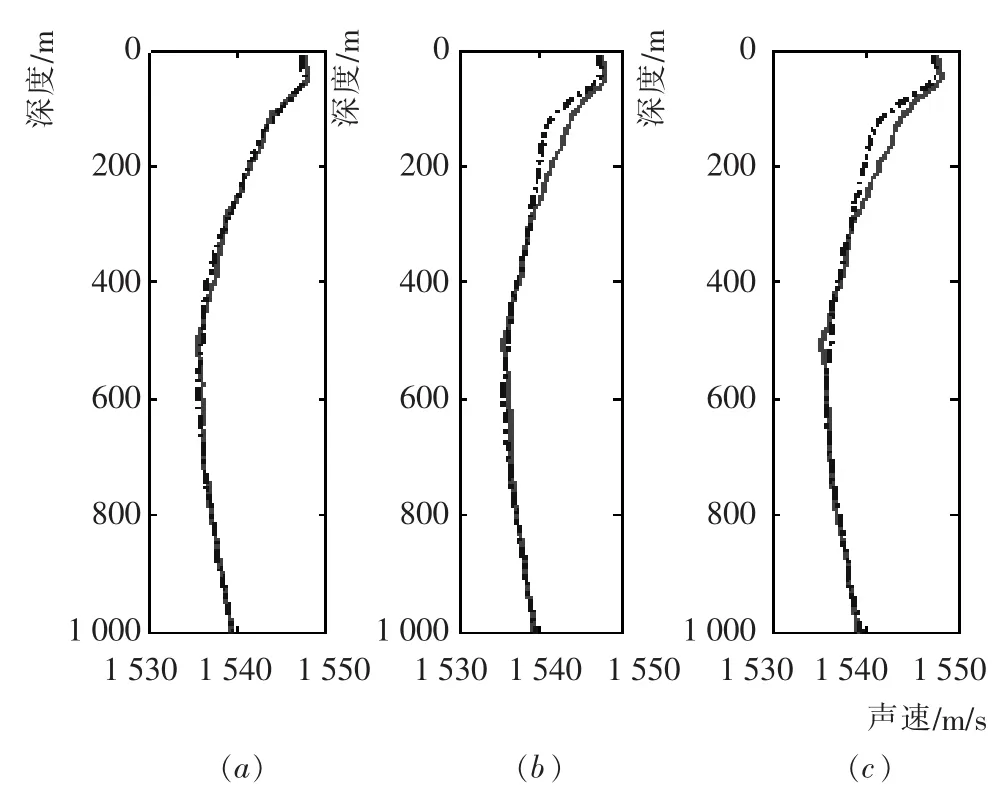
图3 利用不同段观测数据进行重构的结果Fig.3 Reconstruction results of different observation data

经计算，利用上段数据重构（如图a所示）的中误差为0．27 m／s，利用中段数据重构（如图b所示）的中误差为0．78 m／s，利用下段数据重构（如图c所示）的中误差为0．75 m／s。图4（a）（b）（c）分别为利用上、中、下段3个剖面数据进行重构的残差图。

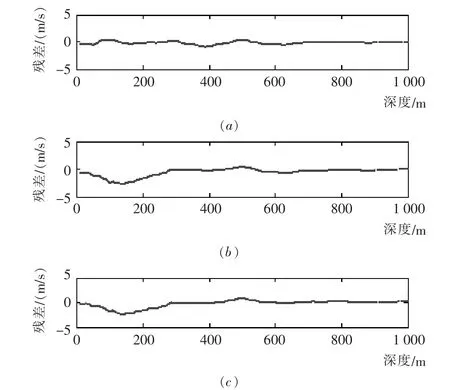
图4 利用不同段观测数据进行重构的残差图Fig.4 Reconstruction residual of different observation data

由图4可以看出：（1）在水深150m左右处，利用3段数据重构的精度都较差。其中，图（a）出现较大的正偏差，图（b）和图（c）出现较大的负偏差。（2）在水深500 m左右处，3幅图均出现较大的正偏差。（3）残差曲线变化趋势较为一致（除了150 m左右），即重构的结果存在着系统偏差。系统偏差可能是由于选取较少阶EOF对剖面进行重构而造成部分信息损失引起的。（4）下层海水声速的重构效果较好，上层海水声速的重构效果稍差。这可能是由于上层海水中海洋要素（如温度、盐度等）变化较为复杂而下层海水海洋要素较为稳定所致。

2．2 EOF方法与内插方法的比较

重构区域海水某处的声速剖面时，较常用的方法是利用目标位置周围的若干个已知声速剖面数据，通过内插得到所需数值。实验采用反距离加权插值法，权函数选择d-2（d为距离），利用待求位置（22．3°N，124．5°E）周围4个已知的ARGO声速剖面数据进行内插，得到该位置所处的声速剖面。将实验区域的已知声速剖面内插成100层以10 m为间距的数据。在每一层数据上，均利用反距离加权法进行内插，即可得到待求的声速剖面，结果如图5所示。经计算，采用内插方法重构声速剖面的中误差为0．63 m／s。由图5可以看出，800 m以下的内插精度较高，800 m以上的内插精度稍差，插值的精度总体上与EOF方法的重构精度相当。

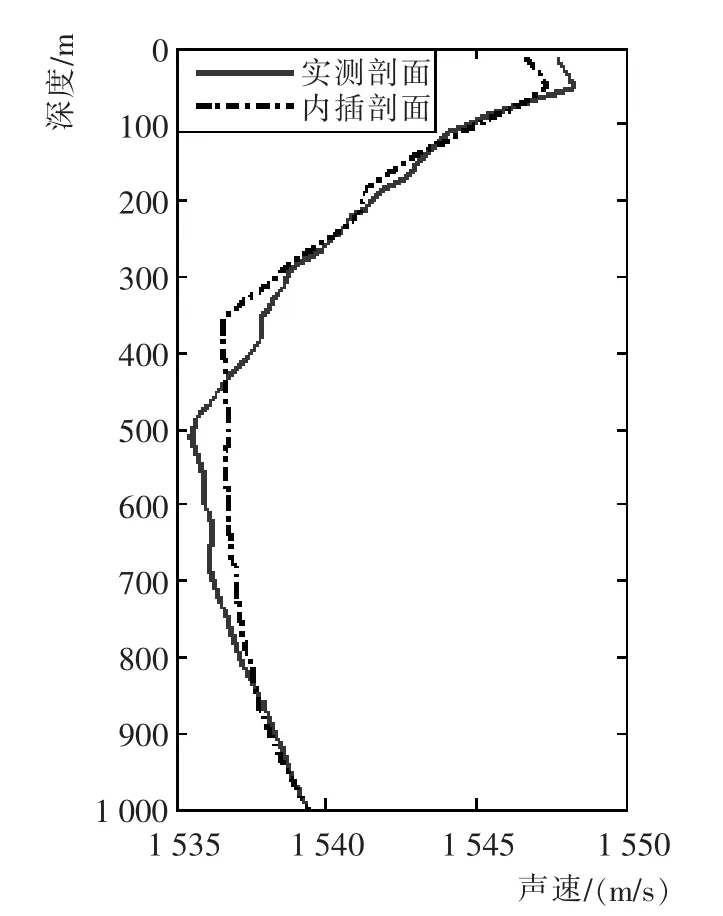
图5 内插方法重构的声速剖面图Fig.5 Sonic speed profile of interpolation

将用内插方法与用EOF方法重构的声速剖面残差进行比较，如图6所示。

由图6可以看出，在上层海水（0～500m）范围内，内插得到的剖面误差较小；在下层海水（500～1000 m）范围内，利用EOF方法重构的精度较高。

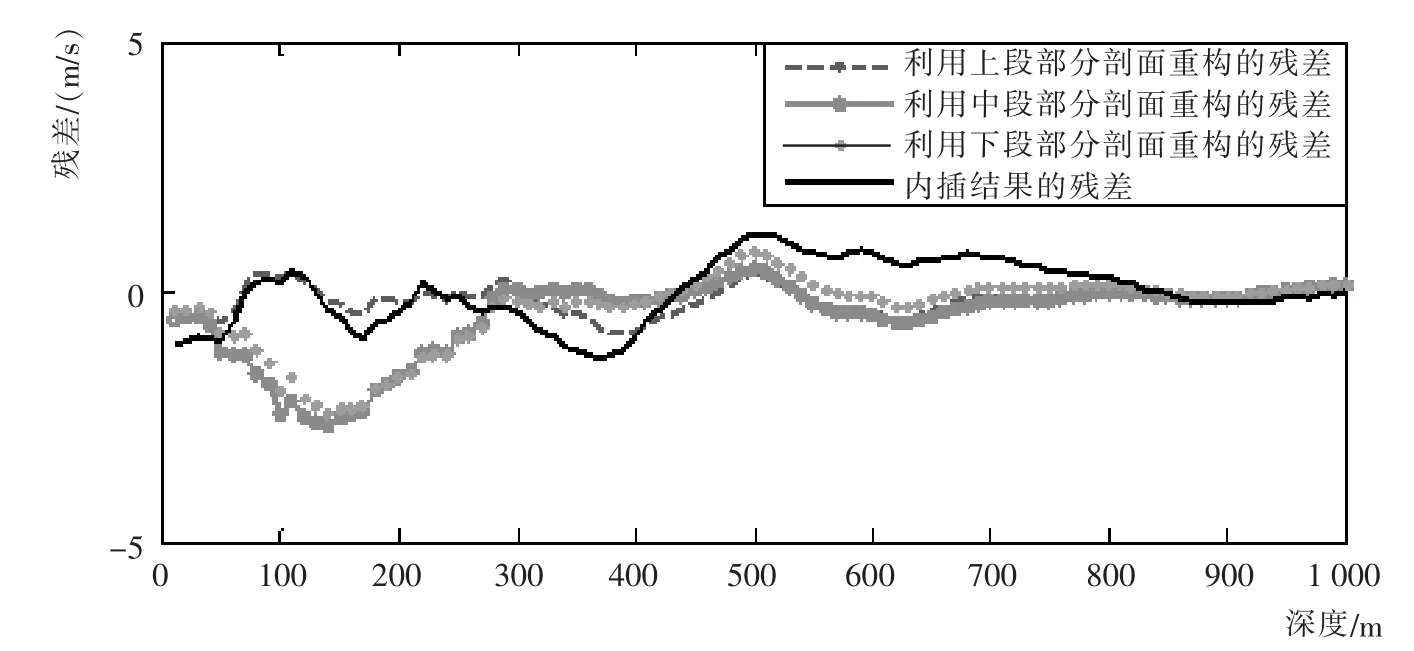
图6 基于EOF重构与距离加权内插的残差比较Fig.6 Residual comparison of EOF reconstruction and distance weighting interpolation

应用内插方法求解某位置处的声速剖面时，需要利用该位置周围已知的浮标剖面数据。因此，用内插法计算试验区域内任意位置处的声速剖面时，需要储存整个区域内的已知声速剖面数据。而且，内插不同位置处的剖面需要不同的已知数据，计算较为复杂。基于EOF方法进行剖面重构，仅需存贮该区域内的前几阶EOF数据，就可重构出区域内任意位置处的声速剖面。同时，重构区域内任意位置处的声速剖面都利用同样的EOF数据，不同的仅是系数矩阵。因此，与内插方法相比，用EOF方法对声速剖面进行重构显得更为方便，而且还有较高的重构精度。

3 结语

利用EOF对ARGO浮标声速剖面进行重构时，使用上段部分剖面数据得到的重构精度较高。与内插方法相比，EOF方法具有较高的重构精度，而且EOF方法仅需要存储较少的数据，就可重构出区域内任意位置处的声速剖面，从而可以避免海量数据的存贮问题。随着ARGO浮标在全球海洋上获得的温度、盐度剖面数据越来越丰富，使用EOF方法重构的精度也将进一步提高。

［1］ 蔡艳辉．差分GPS水下定位系统集成关键技术研究［D］．辽宁：辽宁工程技术大学，2007．

［2］ 于连生．毫米级高精度海水声速测量技术研究［J］．海洋技术，2003，22（3）：63-64．

［3］ 许建平，刘增宏．中国ARGO大洋观测网试验［M］．北京：气象出版社，2007：112-130．

［4］ 杨胜龙，周甦芳，崔雪森，等．ARGO数据研究应用现状与发展趋势［J］．海洋渔业，2007，29（4）：355-358．

［5］ 朱伯康，许建平．国际ARGO计划执行现状剖析［J］．海洋技术，2008，27（4）∶102-114．

［6］ 金国栋，张永刚，张旭，等．基于ARGO数据的海洋声场特征分析及其对作战的影响［J］．舰船电子工程，2008，28 （11）：176-179．

［7］ Dean Roemmich，The argo steering team．Argo the challenge ofcontinuing 10 years ofprogress［J］．Oceanography，2009，22（3）：46-55．

［8］ Russ E·Davis．Predictability of Sea Surface Temperature and SeaLevelPressure Anomaliesoverthe North Pacific Ocean［J］．1976，6（3）：249-266．

［9］ 周士弘，张茂有，周日鹏．海洋声速场的经验正交函数描述及声速剖面预报［J］．海洋通报，1999，18（5）：27-34．

［10］沈远海，马远良，屠庆平，等．浅水声速剖面用经验正交函数表示的可行性研究［J］．应用声学，1999，18（2）：21-25．

［11］沈远海，马远良，屠庆平．声速剖面的分层正交经验函数表示［J］．西北工业大学学报，2000，18（1）：90-93．

［12］韩梅，魏亮，周艳霞．改进型经验正交函数海洋声速剖面预报方法［J］．海洋科学，2000，33（1）：30-33．

［13］张旭．台湾以东海域声速剖面序列的EOF分析［J］．海洋科学进展，2010，28（4）：498-505．

［14］张镇迈，李整林，戴琼兴．南海海域水温重构经验正交基的选取［J］．海洋物理及观测技术，2007，26（5）：228-230．

［15］张镇迈，李整林，戴琼兴．利用有限深度声速数据重构全海深声速剖面［J］．声学技术，2008，27（5）∶106-107．

［16］施能．气象科研及预报中的多元分析方法［M］．北京：气象出版社，2002：91-128．

[责任编辑 杨明庆]

P715．2

B

10．13681／j．cnki．cn41-1282／tv．2017．02．009

2017-01-15

黄河水利职业技术学院校内基金项目：GRACE重力卫星反演黄河流域质量变化关键技术研究（2015KXJS007）。

李洪超（1985-），男，河南永城人，助教，硕士，主要从事高校测绘工程教学与研究工作，研究方向为卫星重力学、海平面变化。