基于EMD分解的径流量预测模型

张承全

（河南省水利第一工程局，河南 郑州 450000）

基于EMD分解的径流量预测模型

张承全

（河南省水利第一工程局，河南 郑州 450000）

径流量是一个非线性、不稳定的时间序列数据。分析了经验模态分解和Hilbert-Huang转换的计算方法，构建了多尺度的预测模型，并以黄河高村站547个月的径流量数据为资料，探讨了应用该模型进行径流量预测的方法。

径流量；EMD；Hilbert；预测模型

0 引言

径流量是一个非线性的、不稳定的时间序列数据。在分析径流量数据时，若采用仅考虑时域的分析方法，往往不能反映瞬时情况。而在一些必要假设的基础上，对观测资料进行处理分析，是体现数据直观价值的重要途径。

数据的分析方法有很多，如小波分析法是一种非线性的处理方法，能够在时域和频域内同时得到较高的分辨率，但会造成许多虚假的谐波，故具有一定的局限性［1］。傅里叶分析法是一种纯时频的数据处理方法，能够在频域内得到非常高的分辨率。但是，它在时域内却失去了分辨能力，对非线性、非稳态数据的处理存在一些不足［2］。1998年，美国国家宇航局的Norden E．Huang首次提出先对一组时间序列数据做经验模态分解 （Empirical Mode Decomposition，简称EMD），再对各个分量进行希尔伯特变换的处理方法，被称为希尔伯特黄变换 （Hilbert-Huang-Transformation，HHT）［3］。EMD能把复杂数据分解成一系列的本征模态函数 （Imtrinsic Mode Function，简称IMF），再对每个IMF进行希尔伯特变换，将得到的频率、振幅、相位进行整合［4～10］。HHT数学模型是利用数据自身的调节机制反映出系统多尺度特性［11～13］。笔者通过对黄河高村站547个月径流量进行EMD分解，构建了多尺度的预测模型，并用该模型进行径流量预测。

1 基本原理

1．1 经验模态分解（EMD）

经验模态分解过程是一个筛选过程，它对非线性序列进行平稳化处理，提取出不同尺度下的波动和趋势因子，进而筛选出其中的本征模态函数IMF。本征模态函数必须满足以下2个条件：（1）该列数据极值点和过零点数目基本相等。（2）在任意时刻，由局部极大点构成的包络线和由局部极小点构成的包络线的平均值为零。

EMD的计算步骤为：（1）寻找数据序列S（t）的所有极大值和极小值，并将其用三次样条函数分别拟合成原数据序列的上、下包络线。（2）对上、下包络线求局部的均值。（3）用原数据序列S（t）减去局部均值m（t），即可得到第一个本征模态函数h1（t）。（4）判断h1（t）是否满足IMF的2个条件，若不满足，就将它看作新的时间序列，重复以上步骤，直到满足IMF条件时，即可得到第一个IMF函数C1（t）。（5）将r1（t）=S（t）-h1（t）看作新的S（t），重复以上步骤，即可依次得到IMF2、IMF3……直到剩余部分R（t）满足给定的终止条件时，筛选结束。此时，原始序列可表示为式（1）。这样，数据序列就由一系列的本征模态函数和一个残值数列组成。

标准差SD的计算式如式（2）所示。一般情况下，前后两个数据的标准差越小，所得的本征模态函数的稳定性就越好，能够分解出的IMF的个数就越多。实践表明，当SD∈（0．2，0．3）时，每个IMF分量都反映了信号在不同时间尺度内的模态特征，并具有较好的稳定性。

1．2 Hilbert变换

原数据序列经过EMD分解后，再按照式（3）对其每一个IMF分量进行Hilbert变换。

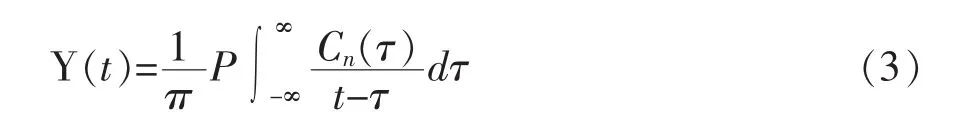
式中：P表示柯西主值。

由于C（t）和Y（t）为共轭复数对，于是可以得到一个解析信号Z（t），如式（6）所示。

式中：a（t）是瞬时振幅函数；θ（t）是相位函数，θ（t）=arctan。

由此可知，经Hilbert变换得到的瞬时振幅和瞬时频率都是随时间变化的函数，所得的瞬时频率能够揭示数据的真实物理意义。

2 模型分析

2．1 技术路线

模型操作的具体流程如图1所示。

2．2 模型建立

根据EMD和HHT变换理论，结合数据特征，构建预测模型，如式（5）所示。

式中：S（t）为月均径流量，亿／m3；t为时间，年；a是各IMF分量的平均振幅；T是各IMF的平均周期；R（t）是残值项；n是变换后分量的个数；b是各函数的初相位。

对式（5）求解可得式（6）。

3 山东高村水文站月径流量多尺度分析及预测模型

高村水文站是黄河流入山东的重要控制站，测验河段位于黄河下游游荡河段的末端，断面距河口579．1 km，集水面积为734 146 km2。本文选取黄河高村水文站547个月的径流量数据进行分析，数据来源于《中国河流泥沙公报》和《黄河水资源公报》。

3．1 多尺度分析

将山东高村水文站547个月的月均径流量进行EMD分解，结果如图2所示。由图2可以看出，山东高村水文站547个月的月均径流量经EMD分解，成为5个本征函数IMF分量和1个残余函数。IMF1振荡频率最高，从IMF1到IMF5的频率逐渐变低，振幅逐渐减小。但是，在IMF4和IMF5中，振幅出现了异常。这种情况时常会出现在低频部分，但不会影响整体的变化趋势。最后一项是残差相，它单调地体现序列的趋势，即径流量有减弱的趋势。

图1 技术路线图Fig．1 Technical circuit

对各个IMF分量进行HHT变换，可得到IMF分量平均幅度和平均频率，如表1所示。

由表1可知，IMF1是从时间序列中分解出的振幅最大、频率最高、波长最短的波动，其平均周期在4．78个月左右波动，平均振幅为511．82亿m3／月；IMF2平均周期在13．84个月左右波动，平均振幅为381．67亿m3／月；IMF3平均周期在29．15个月左右波动，平均振幅为338．99亿m3／月；IMF4平均周期在86．8个月左右波动，平均振幅为408．32亿m3／月；IMF5平均周期在313．86个月左右波动，平均振幅为385．41亿m3／月。IMF1～IMF5各本征模态函数的振幅逐渐变小、频率逐渐变低，波长越来越长。这种变化趋势一直持续到频率已经很低的IMF4。IMF5的波动振幅比IMF4的波动振幅大。这是EMD中经常会出现的异常情况，但它只可能出现在频率较低的部分，不会影响整体的变化趋势。可见，高村站547个月月均径流量主要以4．78和13．84为主进行波动。

图2 高村站547个月月均径流量分解的IMF分量及趋势项Fig．2 IMF component and trend of Gao village station average runoff decomposition for 547 months

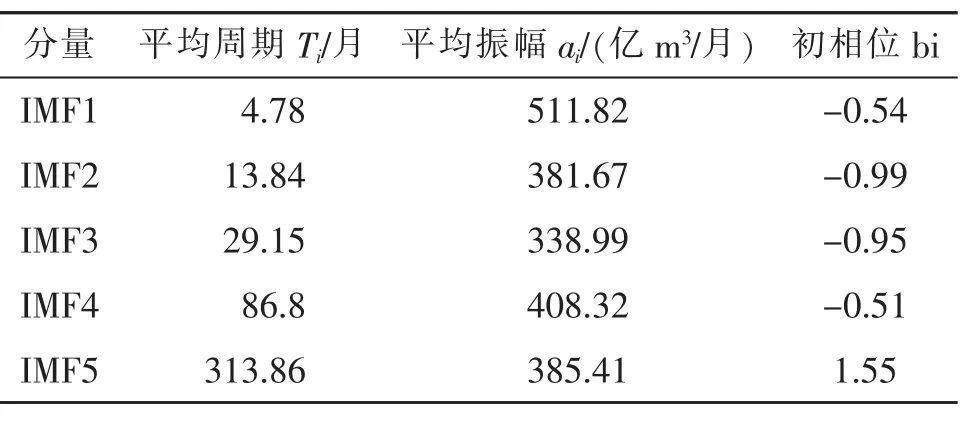
表1 IMF分量平均幅度和平均频率Tab．1 Average amplitude and average frequency of IMF component

3．2 预报模型

根据EMD分解和HHT变换后得到黄河高村站径流量的周期、振幅和初相位，建立2种不同的非线性水文模型。

模型一为未考虑初相位的模型，表达式如式（7）所示。模型二为考虑初相位的模型，表达式如式（8）所示。

3．3 模型的预测

采用模型对黄河高村站第548～552月径流量进行预测检验，结果如表2所示。由表2可知，预测结果与实测值接近，误差在-4%～10%之间。

表2 第548～552月预测结果和相对误差Tab．2 Prediction results and relative error from 548-552 month

4 结语

（1）EMD分解法是对非线性序列进行平稳化的过程，提取数据的客观规律。HHT变换是一种在时域和频域中应用较好的处理方法。将他们结合起来，用于径流量的预测，可为防洪工作提供依据。

（2）用该模型预测黄河高村水文站径流量，结果为：高村水文站月平均径流量的波动准周期为4．78月、13．84月、29．15月、86．8月、313．86月。其中，以4．78月和13．84月为主要震荡周期。预测误差在-4%～10%之间，预测精度较高，满足相关要求。

（3）模型在进行趋势项数据处理时，做了简化处理，HHT缺乏完善的数学理论支持。对于这些不足之处，还需要进一步研究。

［1］ Long S R，Lai R J，Huang N E，et al．Blocking and trapping of waves in an inhornogeneous flow［J］．Dyu Atmos Oceans，1993，20：79-106．

［2］ Farge M．Wavelet transforms and their applications to turbulence［J］．Ann Rev Fluid Mech，1992，24：395-457．

［3］ Huang N E，Zheng S，Steven R，et al．The empirical mode decomposition and the Hilbertspectrum for nonlinear non-stationary time Series Analysis［A］．Proc R Soc Lond A，1998：454；903-995．

［4］ 李新杰，胡铁松，郭旭宁，等．不同时间尺度的径流时间序列混沌特性分析［J］．水利学报，2013，44（5）：516-520．

［5］ 李艳玲，张云鹏，张国玮，等．非线性多尺度模型及其应用［J］．数学的实践与认识，2015，45（1）：203-208．

［6］ Falconer I，Gottwald G A，Melbourne I，et al．Application of the 0-1 Test for chaos to experimental data［J］．SI?AM Journal on Applied Dynamical Systems，2007，6（2）：395-402．

［7］ 邓拥军，王伟，钱成春，等．EMD方法及Hilbert变换中边界问题的处理［J］．科学通报，2001，46（3）：257-263．

［8］ 周念成，王予疆，陈刚，等．低频振荡模式辨识中信号非线性去除的平滑先验方法［J］．电力系统保护与控制，2012，40 （11）：1-5．

［9］ 戴吾蛟，丁晓利，朱建军，等．基于经验模式分解的滤波去噪法及其在GPS多路径效应中的应用［J］．测绘学报，2006，35（4）：321-327．

［10］孙娴，林振山．HHT新技术及其对ENSO的诊断［J］．气象，2006，32（9）：17-22．

［11］Norden E Huang，Zheng Shen，Steven R Long，et al．Theempiricalmodedecomposition andtheHilbert spectrum for nonlinear and nonstationary time series analysis［J］．The royal Society，1998，454：903-995．

［12］Bogdan M，Maarten D V，Ivan G，et al．Source separation from single-channel recordings by combining empirical-mode decomposition and independent component analysis［J］．IEEE Trans on Bio-Medical Engineering，2010，57（9）：2188-96．

［13］P Flandrin，G．Rilling，P Goncalves．Empirical modedecomposition as a filter bank［J］．IEEE Signal Processing Letters，2004，2：112-114．

[责任编辑 杨明庆]

Runoff Prediction Model Based on EMD

Zhang Chengquan
（First Water Conservancy Engineering Bureau of Henan Province，Zhengzhou 45000，Henan，China）

Runoff is the nonlinear and unstable time series data．It analyzes the Empirical Mode Decomposition （EMD）and Hilbert-Huang transformation calculation method，establishes multiscale prediction model．Based on runoff data of the Yellow River Gao village hydrologic station for 547 months，it also discusses the method of using this model to predict the runoff．

Runoff；EMD；Hilbert；prediction model

TV121

A

10．13681／j．cnki．cn41-1282／tv．2017．02．003

2016-12-28

张承全（1984-），男，河南新乡人，工程师，主要从事水文及水资源、水利施工方面的工作。