车辆整备状态车体垂弯频率优化方法研究

尤泰文， 周劲松， 任利惠, 宫 岛

(同济大学 铁道与城市轨道交通研究院，上海 201804)

车辆整备状态车体垂弯频率优化方法研究

尤泰文， 周劲松， 任利惠, 宫 岛

(同济大学 铁道与城市轨道交通研究院，上海 201804)

为提高轨道车辆整备状态车体垂向一阶弯曲频率，提出基于灵敏度分析和车下设备弹性吊挂参数设计方法优化车体垂向一阶弯曲频率。以车身型材骨架厚度为设计变量，用模态灵敏度理论对车体垂弯进行优化设计；结合改进车下设备与车体连接方式，研究了不同吊挂形式及刚度对车体垂向弯曲频率的影响。研究结果表明：采用灵敏度分析调整车体敏感部件厚度后，车体垂向一阶弯曲频率由9.70 Hz提升至10.60 Hz，但车体质量相应增加0.93 t；而采用基于车下设备弹性吊挂参数设计的方法，设置下吊设备固有频率为7 Hz时，整备状态车体的垂向一阶弯曲模态频率提升至10.51 Hz，相对而言基于弹性吊挂参数设计的方法更易于实际工程应用且不增加车体结构质量。

轨道车辆；整备状态；垂弯频率；灵敏度分析；弹性吊挂

目前轨道车辆车体广泛采用轻量化设计，在降低车体承载结构质量同时也带来了车体刚度下降的问题，在进行轻量化的同时保证车体具有较高的垂弯频率成为目前国内外专家学者研究的热点。李永乐等[1-3]建立了高速车辆轻量化前后的有限元模型，对比分析了轻量化对车体模态频率的影响，结果表明轻量化后车体各阶模态频率均出现了不同程度地下降；郭祥涛[4]采用灵敏度分析法进行车体轻量化同时使车体静强度得到了提高；邬广铭等[5]将灵敏度分析法用于汽车设计，研究了灵敏度分析法在优化汽车车身模态频率上的应用，提高了白车身前两阶固有频率；宫岛等[6]研究了车下设备对整备状态车体模态频率的影响，结果表明不同的车下设备布置方式对模态频率均有影响，且提出了车下设备和车体模态频率的匹配方法。以上基于灵敏度分析只研究了轨道车辆车体轻量化、强度优化计算及汽车模态频率优化。目前，提高车辆垂向弯曲频率常采用优化车身拓扑结构、调整车辆设备分布、使用新型材料等方法，这些方法实际应用繁琐且效果有限，难以达到预期目的。

基于此，本文以国内某型轨道车辆为研究对象，在前期研究基础上提出基于灵敏度分析与下吊设备悬挂参数设计两种车体垂弯频率优化方案。通过计算与试验，对比分析以上两种方法对车体一阶垂弯频率的优化效果及各自优缺点，提出可广泛应用于轨道车辆整备状态车体垂弯频率的优化方法。

1 整备状态车体有限元模型建立与模态分析

1.1 有限元模型

本文所研究的轨道车辆车体为整体承载无中梁筒形结构，由端墙、侧墙、底架、车顶和裙板五大部分组成。首先建立车体的有限元模型，车身采用四节点的板单元进行离散，车下设备包括电空制动装置、充电器、逆变器、蓄电池和污物箱等，设置这些设备刚性连接于吊挂梁或吊脚处，下吊设备及内饰采用MASS单元模拟。完整的轨道车辆整备状态下车体有限元模型如图1所示。

图1 车体有限元模型

该车体模型共包含2 650 181个单元，813 117个节点，车体材料为低碳钢，其具体参数如表1所示。下吊设备的吊挂方式以电空制动装置为例，刚性连接如图2所示。

表1 车体材料参数

图2 车下设备刚性连接

1.2 计算模态与试验模态对比分析

对车体有限元模型进行整备状态模态分析，计算了其在0～200 Hz范围内的模态，提取了主要振型的模态频率结果如表2所示，计算得到车体的一阶垂向弯曲频率为9.22 Hz。

为了检验有限元建模与计算的准确性，对该车进行模态测试用于检验及修正有限元模型。使用扫频激励信号激励车体，记录振动加速度响应信号，本次试验采用的是垂向冲击激励。通过对激励点进行激励，获得车体模态频率。实车测试时，被试车体采用橡胶弹簧支撑，采用加速度传感器采集信号，测点布置位置如图3所示。

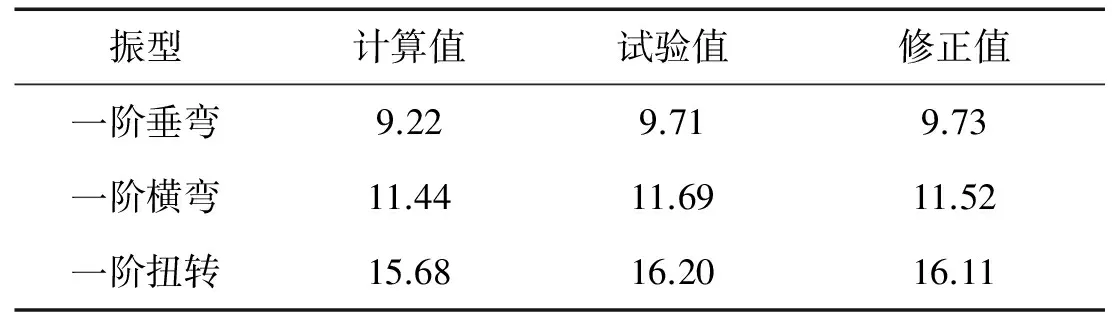
表2 模态频率结果及修正

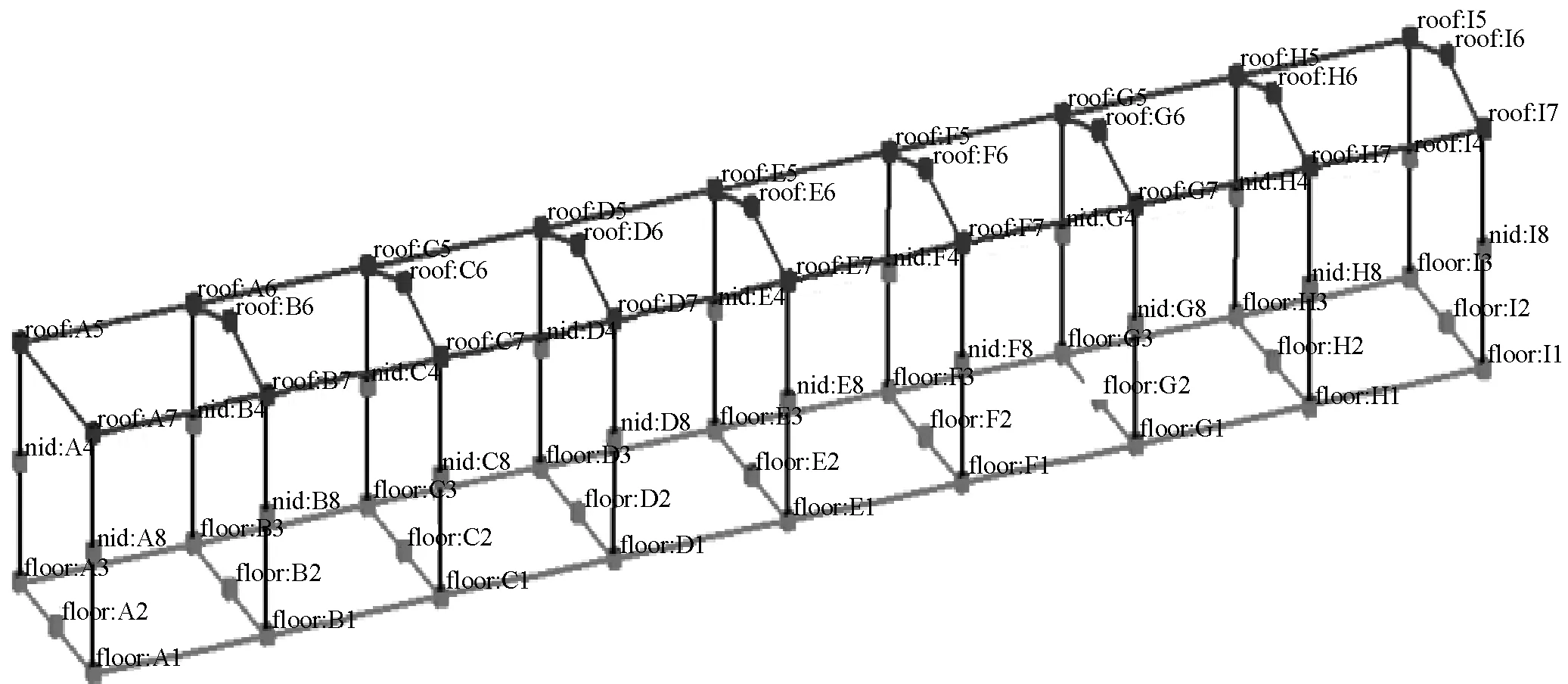
图3 车体模态试验测点

试验结果见表2。有限元计算结果与模态测试结果存在一定的误差，这是由于有限元建模过程中，忽略了车体上个别无法准确模拟的部件，如：车体内装、行李架等，这些部件较为均匀分布在车内，对车体的整体刚度有一定影响。因此，采用当量弹性模量法对初始有限元模型进行修正[7]，将弹性模量增加10%，其结果列于表2，修正后计算结果与试验结果基本一致(最大误差0.5%)。

由于该车体垂向一阶弯曲频率低于10 Hz，不满足轨道车辆动力学标准的相关规定。为此，针对本文研究的轨道车辆车体，进一步进行优化研究。

2 基于灵敏度分析优化车体垂弯频率

2.1 模态灵敏度理论

设ωi及ui分别为车身结构第i阶模态固有频率与振型向量，满足：

(1)

式中:K为结构模型总刚度矩阵;M为结构模型总质量矩阵，其维数即为结构模型自由度数。

对式(1)求导得到：

(2)

式中:ωi,j为ωi对设计变量b(板厚)的偏导数；ui,j为ui对设计变量b(板厚)的偏导数；Kj为K对设计变量b(板厚)的偏导数；Mj为对设计变量b(板厚)的偏导数，j为第j阶导数。

其中：

(3)

在有限元中，K及M分别为单元刚度矩阵以及单元质量矩阵Me的求和，即：

式(4)、(5)对参数b求导,有：

(6)

(7)

式(3)可转化为

(8)

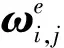
2.2 灵敏度优化分析

车体的质量取决于车体材料及车体结构，采用灵敏度分析法优化车体结构进而改善车体刚度[9]。优化以车体垂弯频率的提高为目的，设置车体整备状态一阶垂弯模态频率为优化目标，以车身质量增幅小于5%为约束条件，分析各部件厚度对车体一阶垂弯模态频率的灵敏度，最终得到各部件厚度的最优解。

对轨道车辆而言，通常车体刚度主要由车体承载结构提供，为避免优化过程中改变其它振型模态频率，使设计变量对设计目标一阶垂弯频率有显著效果，选取车体承载结构的18个主要支撑骨架厚度为设计变量，优化的各部件如图4所示。

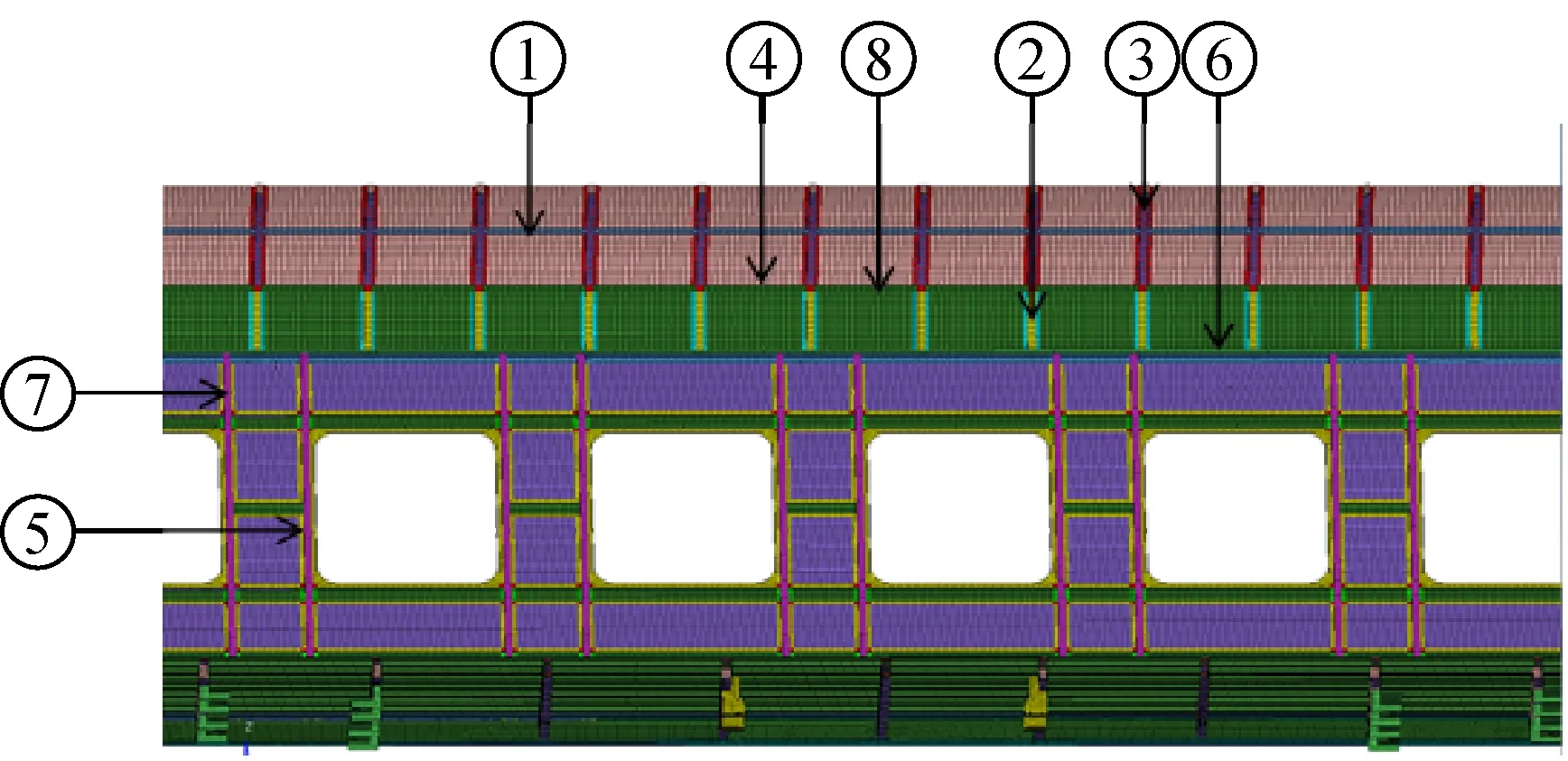
图4 灵敏度优化部件

在优化过程中，初始值为各部件的原始厚度，分别计算了各部件厚度对垂弯频率和车体质量的灵敏度，优化所选设计变量及分析结果如表3所示。

研究表明，灵敏度分析时车体垂弯频率与车体质量会同时提高[10]为避免质量增加对频率的影响保证一阶垂弯频率提高时质量增幅最小，确保车体结构的轻量化，构造新指标来衡量整个构件质量变化对一阶垂弯频率灵敏度的影响，定义相对灵敏度S为

(9)

式中：F为一阶垂弯频率对构件厚度的灵敏度；M为质量对构件厚度的灵敏度。依据上述公式计算得到一阶垂弯频率对车体可调整构件的相对灵敏度结果，如表4所示。

表4中灵敏度值为正表示增加厚度有助于垂弯频率的提高且质量增加最少，灵敏度值为负表示增加厚度会降低一阶垂弯频率同时质量会提升，灵敏度值趋近零值表示该部件厚度变化对于一阶垂弯频率的影响较小。表中，相对灵敏度最高的部件为18号横梁，表面增加横梁厚度对于提高一阶垂弯频率最敏感，其次为13号吊梁，9号、10号边梁。

在优化变量部件允许设计变更的范围内，取相对灵敏度较大的4个构件进行厚度尺寸优化。优化后进行模态分析，结果如表5所示。

对车体结构部件的料厚尺寸优化后，在质量增加2.3%的情况下，垂弯频率提升9.3%至10.60 Hz，其它振型频率未见明显变化。但是该方法在提高一阶垂弯频率的同时，车体本身的自重也在增加，会导致簧上质量增大，这与车体的轻量化设计原则相违背。因而，研究提出一种提高车体一阶垂弯频率而不改变或者降低车体质量的方法更为重要。

表3 灵敏度分析结果

表4 相对灵敏度分析结果

3 基于吊挂参数设计优化车体垂弯频率

整备状态车体由车体承载结构、车辆内装、车下设备以及各连接件组成，其系统振动包含结构的刚体和弹性体振动，是一个刚柔耦合振动系统[12]。为了研究车体与设备间的振动关系，建立车体与吊挂设备的两自由度垂向模型，如图5所示。由于车体结构的模态阻尼比一般在0.015～0.05之间[13]，其对车体固有频率的影响很小，故在该模型中忽略阻尼的影响。

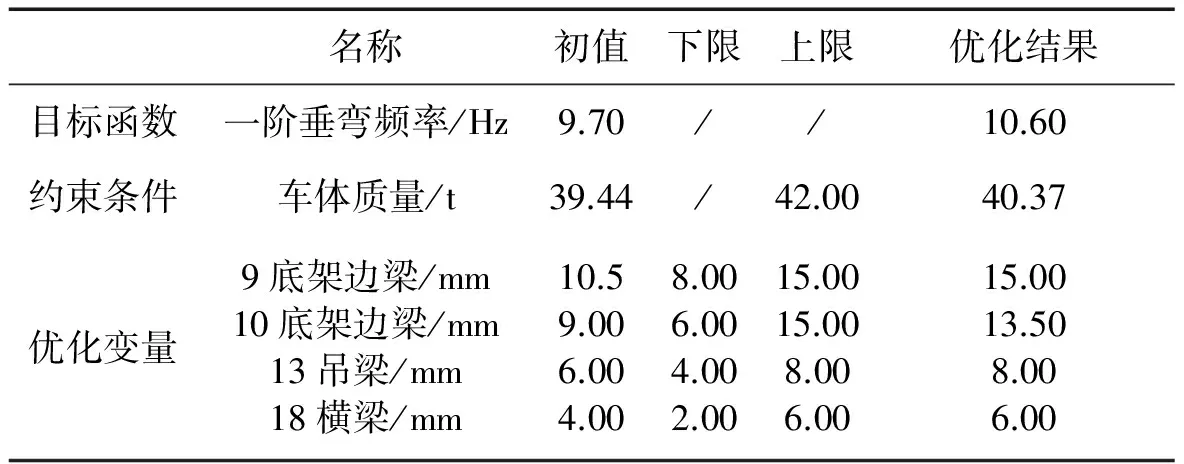
表5 灵敏度优化分析结果

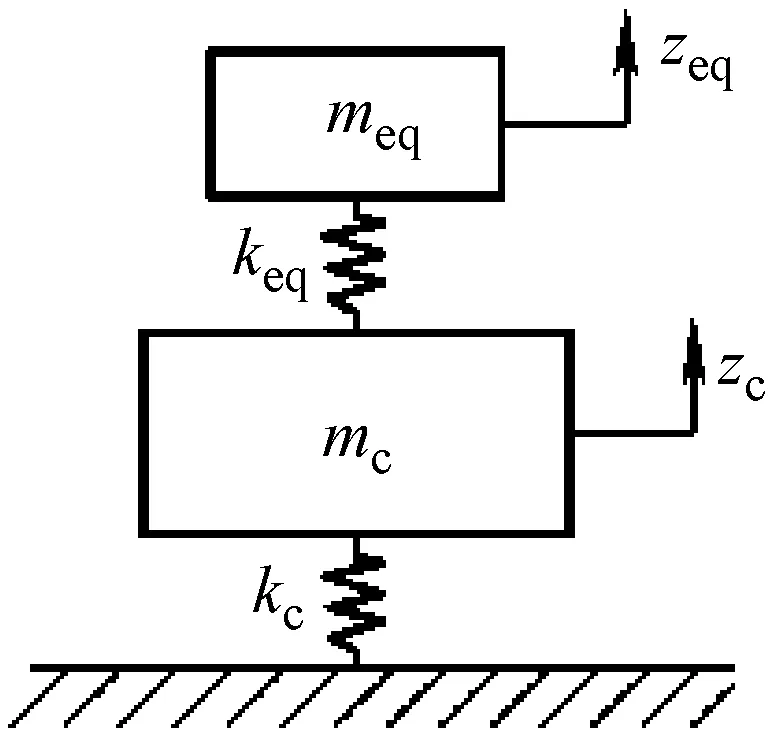
图5 车体及车下设备两自由度模型

图5中，meq为车下设备质量，keq为车下设备吊挂刚度，mc为车体质量；kc为车体弯曲刚度，由于车体弯曲刚度主要由承载结构提供，其余附件对弯曲刚度影响较小，因而针对车体垂向一阶弯曲模态，kc可以表示为

(10)

式中：ms为车体承载结构质量；ωs1为车体承载结构垂向一阶弯曲模态频率。

根据图5等效模型，可以得到耦合系统振动频率解为

ω1=

(11)

ω2=

(12)

由式(11)、(12)可知，当车下设备采用弹性吊挂时，设备与车体构成耦合系统，此时，车体与车下设备的振动分别由低频ω1与高频ω2两种频率振动波叠加而成，即：

(13)

式中:A1与B1分别为车体和设备在低频时振动波的幅值；A2与B2分别为车体和设备在高频时振动波的幅值。

实际设计中通常通过车下设备吊挂元件静挠度来描述吊挂元件，车下设备吊挂静挠度x与吊挂刚度之间关系可用下式描述：

(14)

采用静挠度来描述车下设备吊挂刚度的变化，将车体参数代入，得到系统低频与高频振动频率随静挠度的变化结果如图6所示。图中实线代表低频振动，虚线代表高频振动。

图6中，车体与设备为刚性连接时(静挠度为0 mm)，系统表现为单自由度系统，振动频率为9.70 Hz；随着吊挂结构静挠度逐渐增大，低频振动频率逐渐降低，高频振动频率急剧下降，车体垂弯频率从低频振动转向高频振动，车体与设备之间由刚性连接转向弹性连接，从单自由度系统向两自由度系统转变。

随静挠度继续增大，车体与设备之间连接刚度逐渐降低，两自由度系统向只有车体的单自由度系统转变，低频振动频率向0 Hz趋近，垂弯振动频率趋近于无下吊时整备状态车体垂向一阶弯曲频率10.97 Hz。因此，采用弹性吊挂方式可以提高车体垂弯频率，本节以车下设备的吊挂方式及吊挂参数作为研究对象，研究提高车体垂弯频率的方法。

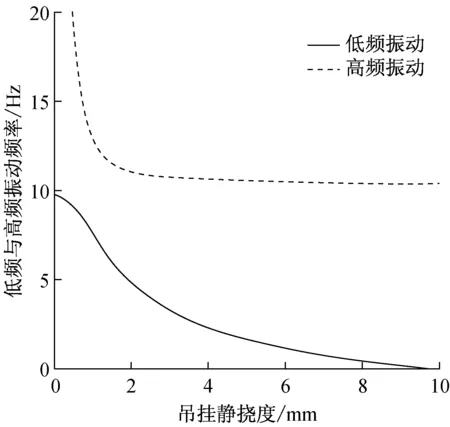
图6 振动频率随吊挂静挠度变化

本文选用橡胶作为弹性隔振元件，采用三维弹性单元模拟橡胶元件，在上述刚性吊挂处，用弹性单元代替刚性连接单元[14]。弹性单元的刚度由下式可得：

(15)

式中:keq为设备吊挂刚度;feq为设备吊挂频率;kd为弹性元件的动刚度值，随着环境温度、振动频率、橡胶材料变化而变化，取值一般在1.2～2.8，本文选取1.4[15]。图7所示为车下设备采用弹性吊挂时的有限元局部模型。结合隔振设计理论[15]，将设备的吊挂频率设定为6 Hz、7 Hz、8 Hz和9 Hz，分析车体整备状态下低阶典型模态振型及其对应的频率值。表6为采用不同吊挂参数时车体弹性模态的计算结果。

图7 车下设备弹性连接

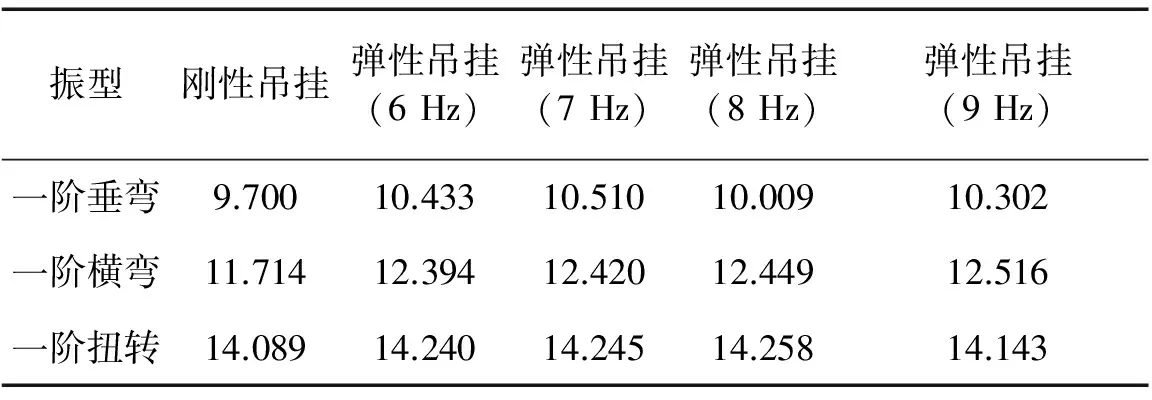
表6 弹性吊挂车体模态频率结果

由表6可知，将车下设备与车体的连接方式由刚性变为弹性，大部分低阶车体模态振型的频率有不同程度的提高，且不增加车体重量。设备独立吊挂频率取为6 Hz、7 Hz和9 Hz时，一阶垂弯频率的提高较为明显。一般车体一阶垂弯频率在10 Hz左右，若设备频率选取9 Hz易发生共振，影响车辆运行平稳性[16]。因而，优先考虑设计吊挂频率为6 Hz与7 Hz。同时，下吊设备的吊挂频率并不是与车体垂弯频率正相关的，而是在吊挂频率为6 Hz、7 Hz时呈现车体垂弯频率上升，至8 Hz时垂弯频率下降的趋势。

值得注意的是，转向架浮沉频率一般在5～8 Hz范围，但由于车体一系、二系减振器的作用，转向架浮沉振型阻尼比较大[17]，其自振频率范围的振动将明显衰减，轨道不平顺激扰经转向架两系悬挂传递至车体的振动主要集中于2 Hz以下[18]，因此车下设备在该频段内振动能量得到很大程度的抑制。

上述分析表明使用优化车下设备吊挂的方式可以提高整备状态车体垂弯频率，相较于灵敏度分析易于实现，不改变车体质量。

4 结论

(1)本文提出优化整备状态车体垂弯频率的两种方法：将灵敏度分析运用到车体垂弯频率优化，通过改进车体刚度与车体质量达到优化频率目的；吊挂方式优化通过改变车体和设备的耦合振动方式，从而使得该型车辆满足相关车体弹性模态频率标准要求。

(2)用模态灵敏度理论对整备状态车体进行灵敏度分析。根据最优方案和模态分析结果表明：优化后车体垂向一阶弯曲频率提升9.2%，但车体质量增加了2.35%。灵敏度分析可提高车体垂向一阶弯曲频率，但由于质量的增加可能会导致其它模态频率恶化，需进一步研究。

(3)从设备吊挂方式入手，改变设备与车体底架之间的连接方式，减少设备与车体的耦合振动。合理设置车下设备的连接方式和隔振悬挂参数可有效改善车体垂向一阶弯曲频率。根据本文方案当设备的吊挂频率设计为7 Hz时，车体垂向一阶弯曲频率提升至10.51 Hz，同时车体质量增加亦不明显。

[1] 李永乐，周乐家，李晓燕. 高速列车钢质拖车车体轻量化设计研究[J].铁道车辆，2002，40(6)：13-21.

LI Yongle, ZHOU Lejia, LI Xiaoyan. Lightening design and research on steel trailer car bodies of high speed trains[J]. Rolling Stock, 2002,40(6):13-21.

[2] 沈宏峻，周劲松，薛向东，等. 铰接式客车车体的轻量化设计和模态分析[J].铁道学报，1997(19):46-51.

SHEN Hongjun, ZHOU Jinsong, XUE Xiangdong, et al. Optimized lightening design and modal analysis of articulated car body[J]. Journal of the China Railway Society, 1997(19):46-51.

[3] 姚曙光，田红旗，许平. 重载敞车车体结构轻量化设计[J]. 交通运输工程学报，2011，11(1): 31-35.

YAO Shuguang, TIAN Hongqi, XU Ping. Lightening design of carbody structure for heavy haul gondola[J]. Journal of Traffic and Transportation Engineering, 2011,11(1):31-35.

[4] 郭祥涛. 高速动车组铝合金车体结构分析及基于灵敏度分析的优化[D]. 北京：北京交通大学，2011.

[5] 邬广铭，史文库，刘伟，等. 基于模态灵敏度分析的客车车身优化[J]. 振动与冲击，2013，32(3)：41-45.

WU Guangming, SHI Wenku, LIU Wei, et al. Structural optimization of a light bus body-in-white based on modal sensitivity analysis[J]. Journal of Vibration and Shock, 2013,32(3):41-45.

[6] 宫岛，周劲松，孙文静，等. 高速列车车下设备模态匹配研究[J]. 振动与冲击，2014，33(8)：180-185.

GONG Dao, ZHOU Jinsong, SUN Wenjing, et al. Modes matching between suspended devices and carbody for a high speed rail way vehicle[J]. Journal of Vibration and Shock, 2014,33(8):180-185.

[7] 宫岛，周劲松，孙文静，等. 高速列车车下设备模态匹配及试验研究[J]. 铁道学报，2014，36(10): 13-20.

GONG Dao, ZHOU Jinsong, SUN Wenjing, et al. Modal matching between suspended equipment and car body of a high-speed railway vehicle and in-situ experiment[J]. Journal of the China Railway Society, 2014,36(10):13-20.

[8] KODIYALAM S, YANG R J, GU L, et al. Multidisciplinary design optimization of a vehicle system in a scalable, high performance computing environment[J]. Structural and Multidisciplinary Optimization, 2004,26(3):256-263.

[9] 谢素明，闫雪冬，兆文忠. 基于敏度信息的铝型材高速车体轻量化研究[J]. 铁道学报，2004，26(3): 26-30.

XIE Suming, YAN Xuedong, ZHAO Wenzhong. Research on weight lightening of the high-speed aluminum-profile car body based on sensitivity information[J]. Journal of the China Railway Society, 2004,26(3): 26-30.

[10] 丁莉芬，缪龙秀. 基于灵敏度分析的结构动力修改方法研究[J]. 铁道学报，1999，21(4): 18-20.

DING Lifen, MIAO Longxiu. Study of structural dynamics modification based on sensitivity analysis[J]. Journal of the China Railway Society, 1999,21(4):18-20.

[11] 陆正刚，郭慧明. 柔性车体振动和运行平稳性控制研究[J].中国机械工程，2006，17(10):416-420.

LU Zhenggang,GUO Huiming.Flexible vehicle vibration active control and ride quality improvement[J].China Mechanical Engineering,2006,17(10):416-420.

[12] NETTER H. New aspects of contact modeling and validation within multibody system simulation of railway vehicle[J]. Vehicle System Dynamics,1997,29(1):246-269.

[13] 黄彩虹，曾京，邬平波，等. 铁道客车车体弹性振动减振研究[J]. 工程力学, 2010,27(12): 250-256.

HUANG Caihong, ZENG Jing, WU Pingbo,et al. Study on carbody flexible vibration reduction for railway passenger carriage[J]. Engineering Mechanics, 2010,27(12): 250-256.

[14] 徐凤妹，劳世定. 客车车下设备吊挂方式的研究[J]. 铁道车辆，2009，47(4): 12-14.

XU Fengmei, LAO Shiding. Research on the hanging mode of equipment under passenger cars[J]. Rolling Stock, 2009, 47(4): 12-14.

[15] 高阳，孙玲玲，王晓乐. 考虑设备弹性的隔振系统[J]. 噪声与振动控制，2014，34(4):138-147

GAO Yang, SUN Lingling, WANG Xiaole. Isolation effect of the system with equipment support’s flexibility[J]. Noise and Vibration Control, 2014,34(4):138-147.

[16] 宫岛，周劲松，孙文静，等. 高速列车弹性车体与转向架耦合振动分析[J]. 交通运输工程学报，2011，11(4): 41-47.

GONG Dao, ZHOU Jinsong, SUN Wenjing. Analysis on the coupled vibration between flexible car body and bogies of high speed railway vehicles[J]. Journal of Traffic and Transportation Engineering, 2011, 11(4):41-47.

[17] 周劲松，宫岛，孙文静,等. 铁道客车车体垂向弹性对运行平稳性的影响[J]. 铁道学报, 2009，31(2)：32-37.

ZHOU Jinsong, GONG Dao, SUN Wenjing, et al. Influence of vehicles elasticity of car body of railway passenger vehicles in ride quality[J]. Journal of the China Railway Society, 2009，31(2)：32-37.

[18] 任尊松，刘志明. 高速动车组振动传递及频率分布规律[J]. 机械工程学报, 2013，49(16)：1-7.

REN Zunsong，LIU Zhiming. Vibration and frequency domain characteristics of high speed EMU[J]. Journal of Mechanical Engineering，2013，49(16)：1-7.

Optimal design of modal frequencies for railway vehicle car-bodies

YOU Taiwen, ZHOU Jinsong, REN Lihui, GONG Dao

(Institute of Rail and Transit, Tongji University, Shanghai 201804, China)

The sensitivity analysis and design of flexible suspension parameters of hanging devices were proposed to improve the first order vertical bending frequency of the fully equipped car bodies. The vertical bending frequency was optimally designed with the thickness of body frame as design variables based on the modal sensitivity analysis theory. The influence of suspended forms and rigidity of rubber on the first vertical bending frequency was analyzed. The results show that the first vertical bending frequency of the car body can be changed from 9.70 Hz to 10.60 Hz while the mass of car body was increased by 0.93 t. The first vertical bending frequency of FE models of fully equipped car bodies was enhanced to 10.51 Hz by adopting the method of flexible suspension while the mass of the car body was constant. In contrast with the sensitivity analysis, the design of flexible suspension parameters of hanging devices is easier for engineering application and the mass of car body is constant.

railway vehicle; severing condition; bending modal frequency; sensitivity analysis; flexible suspension parameter

“十二五”国家科技支撑计划项目(2015BAG19B02)

2015-11-11 修改稿收到日期：2016-04-11

尤泰文 男,博士生,1992年生

周劲松 男，博士，教授，博士生导师，1969年生

U270.1

A

10.13465/j.cnki.jvs.2017.08.014