复小波离面振动检测的研究
尹爱军, 李 江, 张 泉
(重庆大学 机械学院 机械传动国家重点实验室, 重庆 400044)
复小波离面振动检测的研究
尹爱军, 李 江, 张 泉
(重庆大学 机械学院 机械传动国家重点实验室, 重庆 400044)
基于图像的振动检测技术是一种大范围、非接触的振动检测技术,得到了广泛的研究。针对一般视觉检测中的图像特征提取等问题,提出了基于复小波分解的离面振动测量方法,推导了图像复小波变换系数相位变化与结构离面振动位移之间的关系。同时对悬臂梁和电机进行了验证测试实验,并与有限元仿真、边缘检测以及常规加速度振动检测进行了对比,结果表明该方法可以准确提取出振动频率信息,并且系统简单、成本低、不需要特征跟踪、边缘提取等复杂算法。
复小波变换; 离面振动; 振动检测; 机器视觉
振动测量在现代机械、航空、航天等领域中具有重要作用,它是一种对装备服役状态进行检测和评估,保障装备可靠安全运行的重要方法[1]。传统的接触式、激光等振动检测方法存在空间分辨率低,易影响结构力学特性等问题[2]。
基于机器视觉的振动测量是一种大范围、非接触振动检测方法,得到了广泛的研究。王运付[3]提出了一种基于干涉条纹移动的振动测量方法。杨福俊等[4]采用单幅数字散斑图投影及高速图像采集技术,研究了动态离面位移的测量。WANG等[5]利用切比雪夫矩描述子对图像的边界特征进行分析,得到了复合板的结构模态。张春芳[6]利用多个相机,提取出了在轨天线的振动信息,验证了利用双目立体视觉进行三维振动测量的正确性和可行性。WANG等[7]运用模糊图像序列分析出了低频振动参数以及高频振动幅值。这些研究方法光路复杂,实验设备昂贵,甚至需要精确跟踪图像特征。因此,测量的结果在一定程度上会受到相机性能与特征提取的影响。
复小波变换是实小波变换(DWT)在复数域的推广。在机器视觉领域得到了较广泛的研究。李辉等[8]提出了一种改进双树复小波变换算法,准确识别出了轴承的故障类型。SAMPAT等[9]通过将复小波与结构相似性测量相结合,提出了一种对几何失真图像的相似度评价的算法。
本文探讨了离面振动中图像的变化关系,推导了图像复小波变换系数的相位变化与离面振动位移之间的关系。最后,通过本文所提算法进行了悬臂梁与电机的振动测试实验,并与其他振动检测方法进行了对比分析。证明了本文方法是一种常规成像条件下的视觉振动检测方法,无需复杂的光路系统和图像特征提取。
1 离面振动原理
针孔模型在摄像模型中应用最为广泛[10],离面振动针孔模型如图1所示。CCD相机垂直于结构振动方向,在结构离面振动过程中,物距大小会发生改变,从而结构的成像大小和位置也会发生相应的变化。
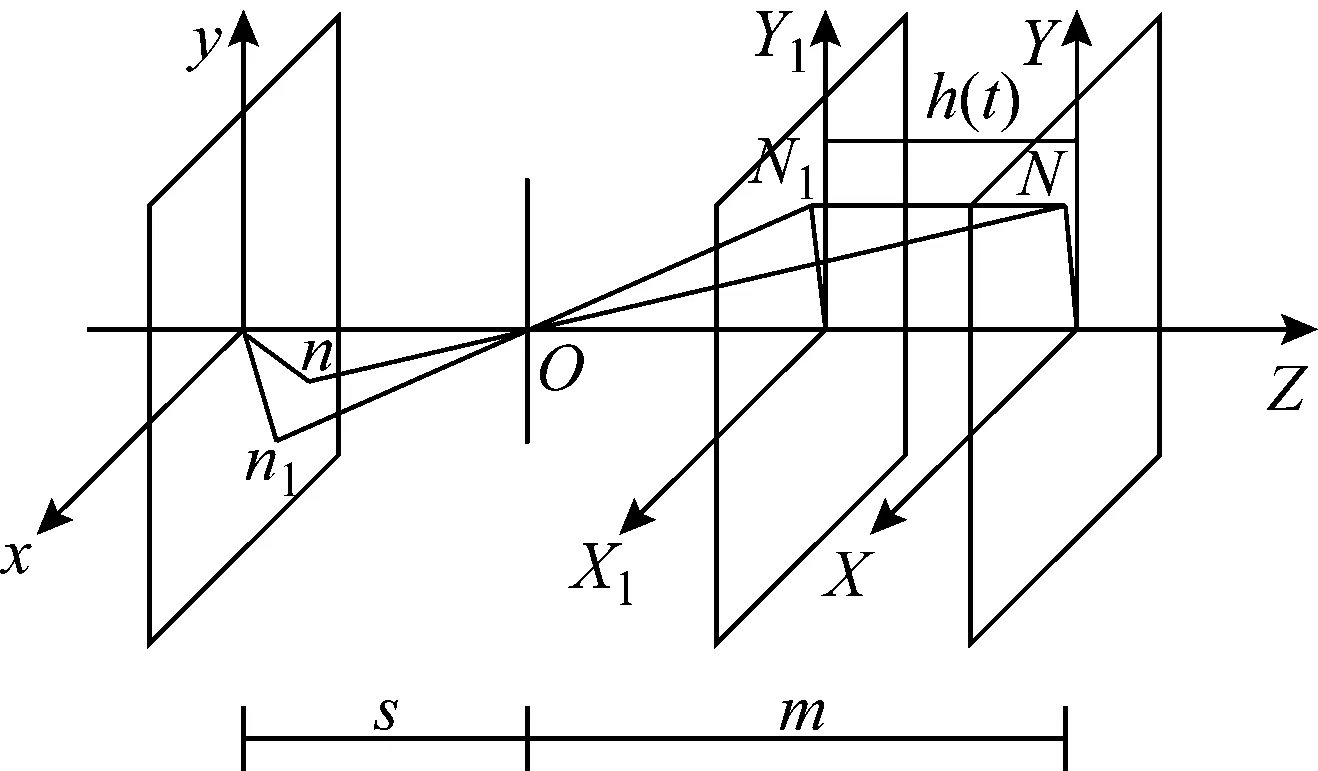
图1 摄像机成像等效针孔模型
图1中,O为相机镜头中心,s为相距,m为物距。初始时刻,结构上点N(X(t0),Y(t0),Z(t0))。其对应的成像点为n(x0,y0)。t时刻,N离面运动h(t)后到N1(X(t),Y(t),Z(t)),其像点为n1(x(t),y(t))。由图1中几何关系知:像点位移
由于结构只作离面运动,所以X(t)=X(t0),故上式进一步化简为
(1)
在本文的视觉振动测量中,由于m远大于h(t),所以式(1)可以简化为
(2)
(3)
同理可得
(4)
2 复小波测振原理
2.1 复小波变换构造
复小波变换是实小波变换在复数域的推广,其变换得到的小波系数为复数,包含了幅值信息和相位信息[11]。
复小波变换的构造方法非常多,COHEN等[12]设计了复正交准解析小波和尺度函数,MAGAREY[13]提出可以用一个基于准解析小波的DWT树来得到复小波系数的复小波变换,KINGSBURY[14]提出了二元双树复小波变换(DTCWT),它是一组正交的DWT实数小波变换对。
本文中,设复小波变换的母小波函数
(5)
式中ωc是带通滤波器的中心频率,在本文中可作常数处理。g(u)是一个缓慢变化的对称函数。
式(5)中母小波函数进行平移、收缩得到小波函数族可表示为
(6)
式中:α为尺度因子;b为平移因子。那么对于一个实信号x(u)其复小波变换可以表示为
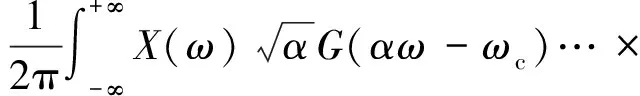
(7)
式中,X(ω)、G(ω)分别为x(u)、g(u)的傅里叶变换。Cx(α,b)为信号x(u)在尺度α下,平移因子b处的连续复小波变换系数。
2.2 复小波系数相位与离面振动位移的关系
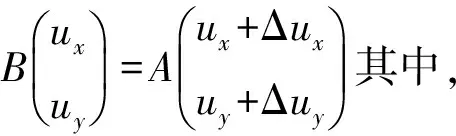
由于二维和一维分析原理相同,为了简便起见,本文着重分析一维情形。设一维信号A(u)与B(u)满足关系:B(u)=A(u+Δu),由傅里叶变换的时移性可知B(ω)=A(ω)ejωΔu,将其代入式(7)得
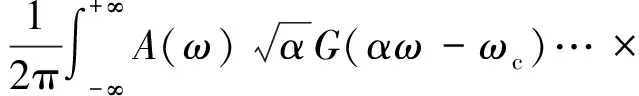
当位移量Δu小于复小波滤波器g(u)的宽度时,上式可表示为
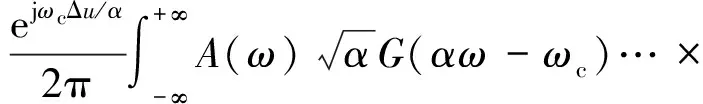
(8)
当g(u)≡1时,式(8)取等号。由式(8)可知,图像A(u)与平移后的图像B(u)复小波分解系数模相等,相位差θ为ωcΔu/α。
设O0为初始图像帧,Oi、Oi+1分别为第i、i+1帧,第i+1帧时刻为t,并设两者水平方向像素位移为Δux(t),其复小波分解系数的相位分别为θi,θi+1,在高速摄像中,Δux(t)远小于滤波器宽度,根据式(8),Oi、Oi+1的相位差为
(9)

(10)
联立式(3)、(4)、(10)可得结构离面振动位移h(t)与相邻帧图像复小波分解系数相位差θ(t)的关系为
(11)
2.3 复小波分解系数相位差的频谱分析
记H(ω),Θ(ω)分别表示对h(t),θ(t)的傅里叶变换,对式(11)左右两端取傅里叶变换,由傅里叶变换的微分性质以及线性性质可得
(12)
(13)
将式(13)表示成模与相位的表达式为(ω≥0)
(14)

3 振动检测对比实验
3.1 悬臂梁检测实验
本文首先进行了悬臂梁振动测试实验,实验系统如图2所示,其中相机为德国Baumer公司的TXG03cCCD相机。实验中,悬臂梁x-y平面为黑白交界的特征线,相机分辨率为140×140,帧率为150 Fps在B点施加锤击激励。
通过图2的实验系统采集悬臂梁的振动视频,用本文的复小波分解以及边缘提取算法分别得到复小波相位差θ(t)(其中分解尺度α=5)、图像边缘位移u(t)的时域波形如图3所示。


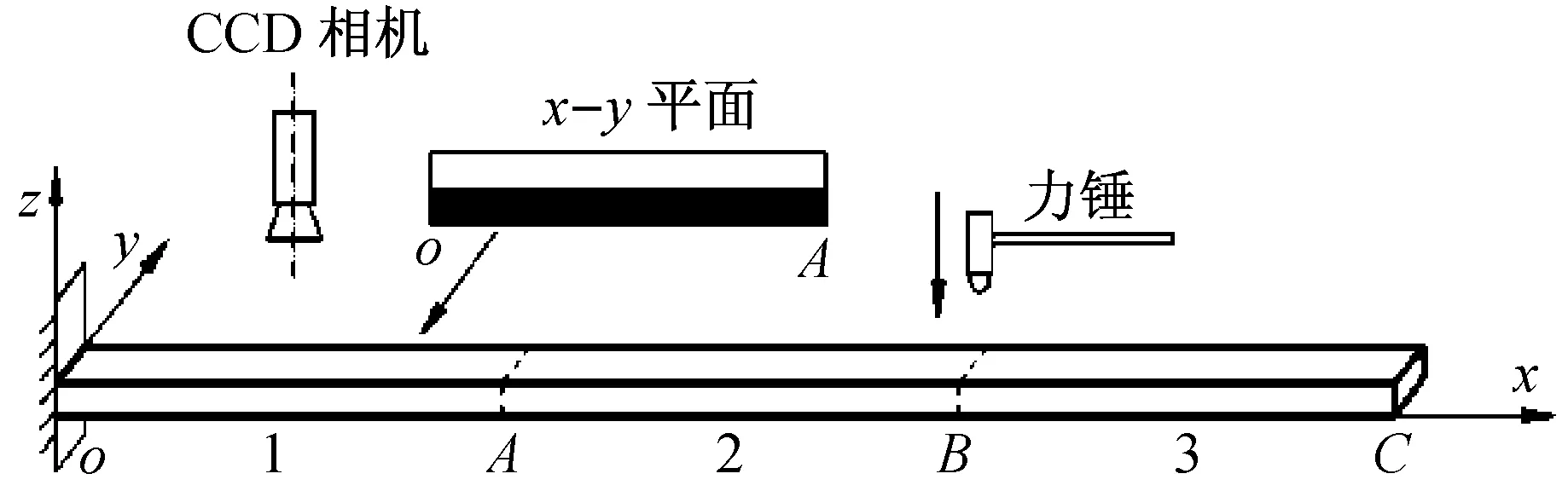
图2 悬臂梁实验图
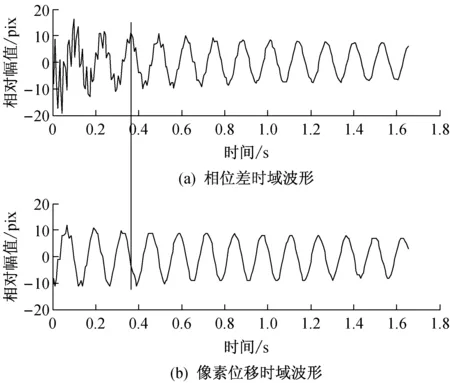
图3 时域波形
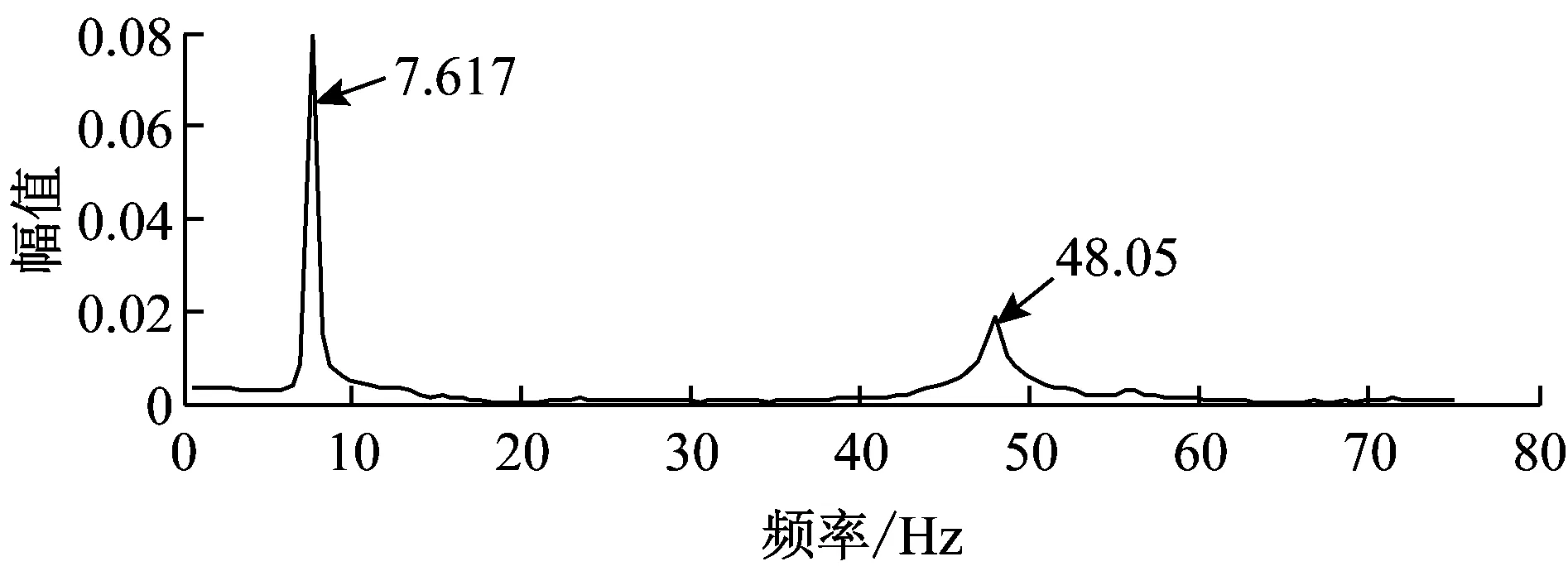
(a) 相位差幅值谱
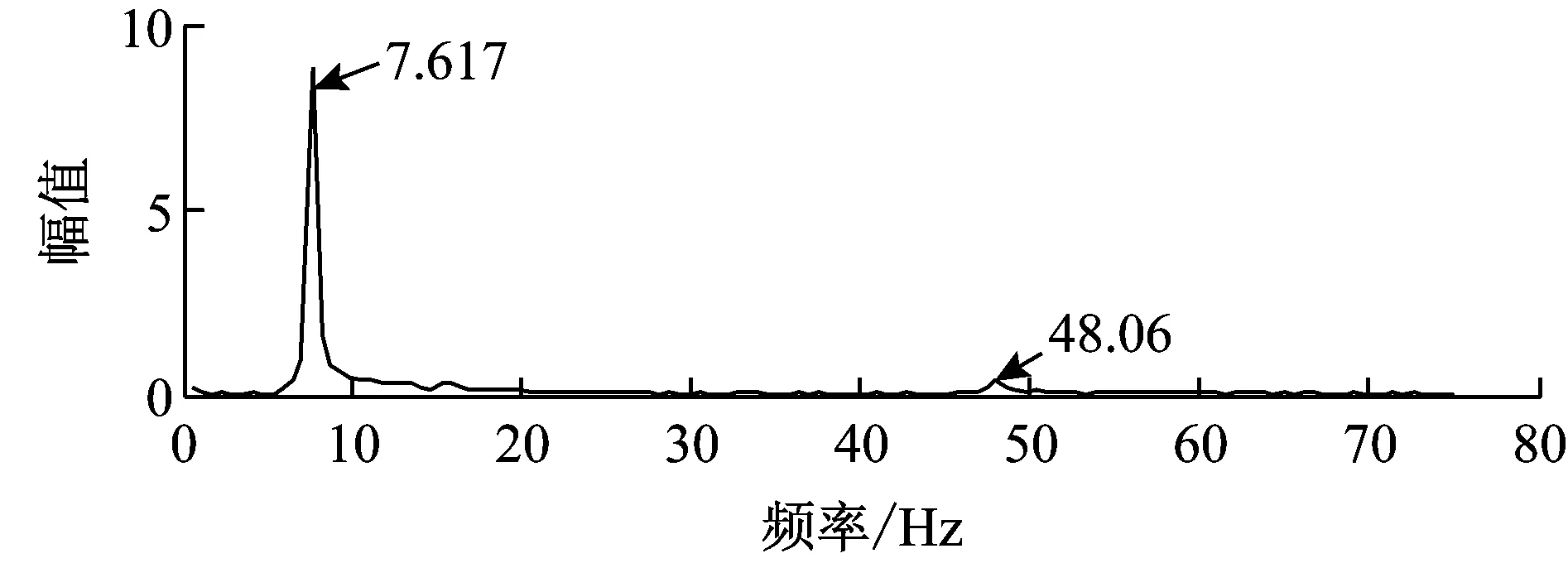
(b) 像素位移幅值谱
图4分别为θ(t)和u(t)的幅值谱。由图4(a),梁的一阶、二阶固有频率分别为7.617 Hz,48.05 Hz,与边缘提取算法所得结果一致。但本文算法的二阶固有频率更为明显,且无需特征提取、边缘识别等复杂图像处理算法。
表1为该悬臂梁的一阶、二阶固有频率检测结果及与ANSYS限元分析的结果对比。

表1 悬臂梁实验结果
对比表1中数据,边缘提取法和本文所提方法固有频率检测结果接近,与仿真结果更为一致,而加速度传感器得到的结果都要小于仿真结果,这是因为悬臂梁安装传感器后,悬臂梁的动态特性发生变化。
3.2 电动机检测实验
为了进一步将本文算法推广到实际复杂机械结构中,本文对电动机进行了振动检测实验,实验系统如图5所示。电机的额定转速为3 000 r/min(振动频率理论值为50 Hz)。

图5 电机实验图
加速度振动信号时域波形图、幅值谱如图6所示,其中传感器为PCB-333B45,采样频率1 000 Hz。
利用本文方法,复小波系数相位差时域波形图、幅频谱如图7所示(分解尺度α=5)。其中CCD相机分辨率为200×200,帧率为150 Fps.
对比分析图6和7,运用加速度传感器测得的电机振动频率为48.83 Hz,而运用本文复小波视觉振动方法测得的电机振动频率为49.8 Hz,与理论值50 Hz更为接近。由此可见,本文的算法可以准确检测出电机的振动频率信息,且误差范围小,精度高。
表2为该电动机的振动频率检测对比结果。
分析表2中数据,边缘提取法测得频率与理论值误差较大,这是因为边缘提取法受算法以及光照环境影响大,需要高分辨率相机和优越的图像处理算法,在复杂机械结构振动检测中,不能保证精确度;而复小波法与理论值接近,且在常规成像条件下,无需边缘识别,特征匹配等即可准确检测出电动机的振动频率。
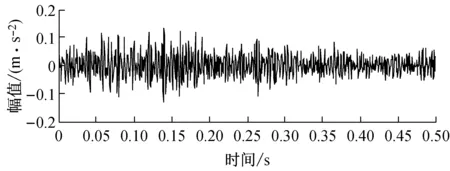
(a) 加速度振动时域波形
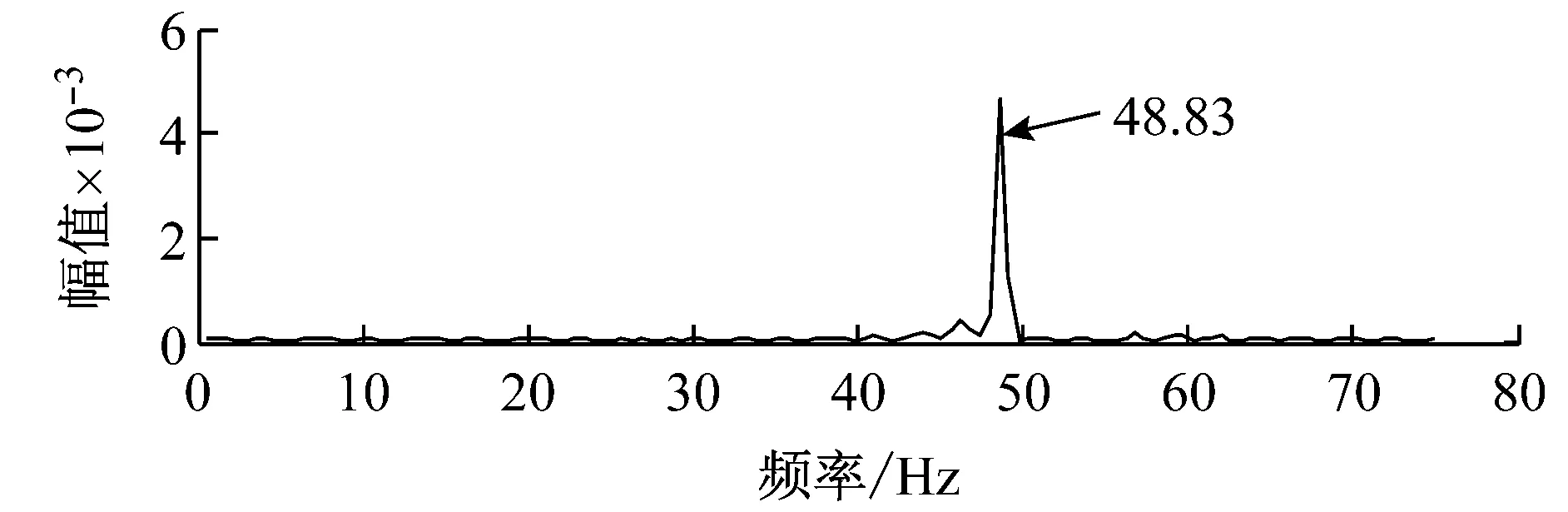
(b) 加速度振动信号幅值谱
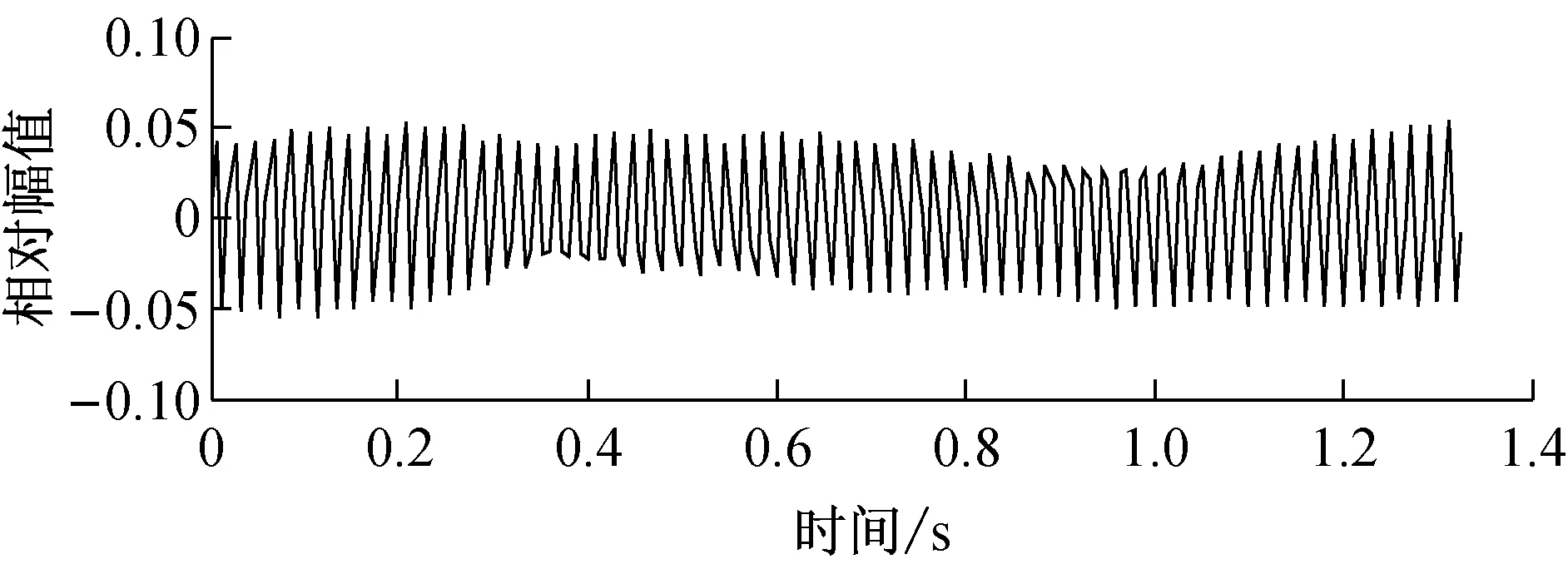
(a) 相位差时域波形
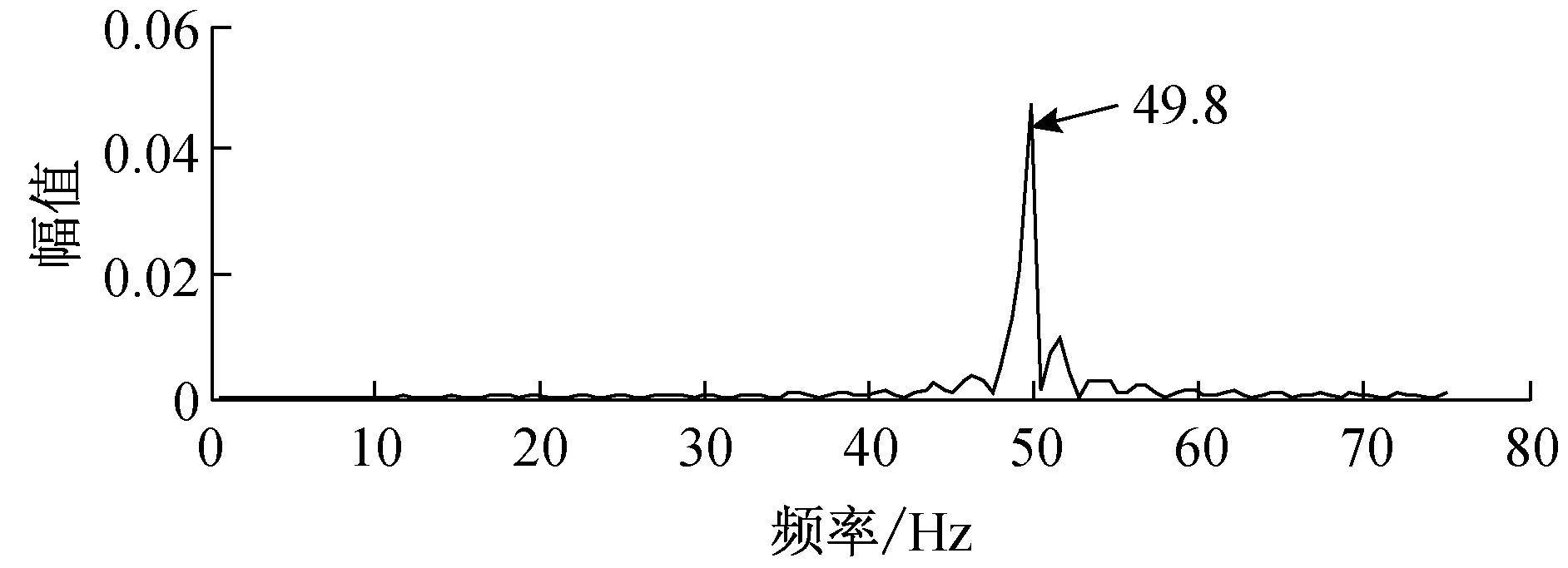
(b) 相位差幅值谱

表2 电动机实验结果
4 结 论
视觉测量方法由于具有大范围、非接触测量等优点,得到广泛的研究与应用。传统的视觉测振方法需要特征跟踪、边缘提取或复杂的光路系统。本文提出了复小波分解系数相位差的离面振动检测方法,建立了检测数学模型,通过悬臂梁和电机的振动检测对比实验表明,本文方法可以准确检测结构特征频率。基于复小波系数相位差的视觉测振方法,实现了常规成像条件下的离面振动检测,系统简单;且无需特征跟踪、边缘提取等复杂的图像处理过程。
[1] 贾书海,李以贵,谭玉山.一种新的数字散斑振动定量分析系统[J].应用光学,2007,28(1):92-96.
JIA Shuhai,LI Yigui,TAN Yushan.A novel DSPI system for vibration quantification analysis[J].Journal of Applied Optics,2007,28(1):92-96.
[2] 徐仲勋,黄科程.基于机器视觉的多目标跟踪技术的研究[J].柳州师专学报,2015,30(2):128-131.
XU Zhongxun,HUANG Kecheng.The research of multi-target tracking based on machine vision[J].Journal of Liuzhou Teachers College,2015,30(2):128-131.
[3] 王运付.线阵CCD激光干涉法振动测量研究[D].成都:电子科技大学,2013.
[4] 杨福俊,房亮,何小元.基于单幅数字散斑投影及图像相关的离面振动测量[J].光学技术,2007,32(3):323-326.
YANG Fujun,FANG Liang, HE Xiaoyuan.Vibration measurement based on speckle projection and digital image correlation methods[J].Optical Technique,2007,32(3):323-326.
[5] WANG W,MOTTERSHEAD J E.Adaptive moment descriptors for full-field strain and displacement measurements[J].Journal of Strain Analysis for Engineering Design,2013,48(48):16-35.
[6] 张春芳.基于双目立体视觉的大型柔性结构在轨振动测量研究[D].哈尔滨:哈尔滨工业大学,2014.
[7] WANG Shigang, GUAN Baiqing, WANG Guobao,et al. Measurement of sinusoidal vibration from motion blurred images[J].Pattern Recognition Letters, 2007,28(9):1029-1040.
[8] 李辉,郑海起,唐力伟.基于改进双树复小波变换的轴承多故障诊断[J].振动、测试与诊断,2013,33(1):53-59.
LI Hui,ZHENG Haiqi,TANG Liwei.Bearing multi-faults diagnosis based on improved dual-tree complex wavelet transform[J].Journal of Vibration,Measurement & Diagnosis,2013,33(1):53-59.
[9] SAMPAT M P, WANG Z, GUPTA S, et al. Complex wavelet structural similarity: a new image similarity index[J].IEEE Transactions on Image Processing, 2009, 18(11): 2385-2401.
[10] 于仕琪,刘瑞祯.学习OpenCV[M].北京:清华大学出社,2009.
[11] 张大波,刘志刚,张亚军.复小波研究现状及其在电力系统中的应用进展[J].电力系统自动化,2006,30(17):97-104.
ZHANG Dabo,LIU Zhigang,ZHANG Yajun.Complex wavelet transform review and its applications in power system[J].Automation of Electric Power System,2006,30(17):97-104.
[12] COHEN A, DAUBECHIES I, VIAL P. Wavelets on the interval and fast wavelet transform[J].Applied & Computational Harmonic Analysis, 1993,1(1):54-81.
[13] MAGAREY J.Motion estimation using complex wavelets[D]. Cambridge: University of Cambridge.
[14] KINGSBURY N.Image processing with complex wavelets[J].Phil Trans R Soc London A,Math Phys Sci, 1999;357(1760):2543-2560.
Research on out-of-plane vibration detection based on CWT
YIN Aijun, LI Jiang, ZHANG Quan
(State Key Laboratory of Mechanical Transmissions, Mechanical College of Chongqing University, Chongqing 400044, China)
Vibration detection based on image technology is a large range, non-contact vibration testing technology, which has been studied widely. Aiming at the problems such as image feature extraction in the visual inspection, the method of measuring out-of-plane vibration based on CWT was proposed in the paper. The relationship between the phases of CWT and the vibration displacement of the structure was deduced. In addition, vibration test experiments on cantilever beam and motor were carried out. Compared with finite element simulation, edge extraction and acceleration sensors, it shows that the method of the paper, which has a simple system, low cost and no need of complex algorithms such as feature tracking, edge extraction, can extract the vibration frequency information accurately.
CWT; out-of-plane vibration; vibration detection; machine vision
国家自然科学基金(51105396);中央高校基本科研业务费(CDJZR13115501)
2015-10-23 修改稿收到日期:2016-03-15
尹爱军 男,博士,教授,1978年5月生 E-mail:aijun.yin@cqu.edu.cn
TH113.1
A
10.13465/j.cnki.jvs.2017.08.010

