基于改进BP神经网络的中药水提液陶瓷膜污染预测研究
窦鹏伟,王珍,佘侃侃,樊文玲
南京中医药大学信息技术学院,江苏 南京 210023
论著·中医药信息学
基于改进BP神经网络的中药水提液陶瓷膜污染预测研究
窦鹏伟,王珍,佘侃侃,樊文玲
南京中医药大学信息技术学院,江苏 南京 210023
目的 为防治中药水提液陶瓷膜纯化过程中的膜污染问题,探索预测污染度的新方法。方法对BP神经网络模型进行改进,利用隐含层最佳神经元数目的快速确定方法、BP神经网络权值和阈值的快速寻优算法,建立中药水提液陶瓷膜污染预测模型,对207组中药水提液数据进行网络训练和预测。结果与多元回归分析、基本BP神经网络、RBF神经网络等模型相比,应用改进BP神经网络模型进行预测实验的拟合误差更小,均方误差仅为0.005 7;此外,改进BP神经网络模型的性能更加稳定,在20次随机运行实验中达到预设目标的成功率高达 95%。结论改进模型具有很好的网络性能、拟合效果和预测能力,能够稳定准确地预测膜污染度。
中药水提液;膜污染;BP神经网络;隐含层神经元;遗传算法
中药水提液的纯化技术是中药制剂前处理中应用最多的工艺方法之一。陶瓷膜因具有耐高温、化学性质稳定、抗污染性强、机械强度高等优点[1],被广泛应用于中药水提液的纯化过程。然而,膜污染是制约陶瓷膜精制中药的关键问题。
膜污染是指由于被过滤液中的微粒、胶体离子、溶质分子与膜存在物理化学作用而引起的各种粒子在膜表面或膜孔内吸附或沉积,造成膜孔堵塞或变小并使膜的透过流量与分离特性产生不可逆变化的一种现象[2]。中药水提液组成复杂,是一种含有悬浮的固体微粒、胶体粒子和完全溶解溶质分子的复杂混悬体,在分离过滤操作时膜极易被污染,造成膜通量锐减[3-4]。目前,中药水提液陶瓷膜膜污染机理尚不明确,过滤过程缺乏系统性理论指导及有效的膜污染控制手段。
中药水提液陶瓷膜膜污染是多种复杂因素综合作用的结果,具有较强的不确定性,难以采用特定函数模型描述。要实现对膜污染的准确预测,需要建立合理实用的预测模型。BP神经网络是近年被广泛应用的一种模拟人脑神经系统结构和功能的人工智能方法,是一种解决非线性、不确定性问题的数学模型,具有连续传递函数的多层前馈人工神经网络,训练方式为误差反向传播算法,并以均方误差最小化为目标不断调整网络的权值和阈值,最终能高精度地拟合数据[5]。BP神经网络具有较强的学习和适应能力,适合针对中药水提液复杂系统建模,在处理具有非线性特点的中药水提液陶瓷膜膜污染预测问题方面,比一般的线性、非线性模型更有优势。
1 BP神经网络
1.1 拓扑结构
BP神经网络是按误差逆传播算法训练的多层前馈网络,通过训练样本来学习和存贮大量输入-输出模式映射关系,无需事先揭示及描述映射关系的数学方程。学习规则采用最速下降法,通过误差反向传播不断调整网络的权值和阈值,使网络的整体误差最小[6-8]。
BP神经网络的拓扑结构包括输入层、隐含层和输出层,其中可包含1个或多个隐含层。各层次的神经元之间形成全互连接,同层神经元之间无反馈连接,见图1。
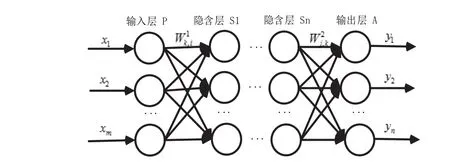
图1 BP神经网络拓扑结构
1.2 基本原理及其缺陷
BP神经网络由信号的正向传播和误差的逆向传播2部分组成[9]。设输入层神经元为P=[p1,p2,…pi],隐含层神经元为 S=[s1,s2,…sk],输出层神经元为表示输入层第i个神经元与隐含层第k个神经元之间的连接权值,表示隐含层第k个神经元与输出层第j个神经元之间的连接权值;隐含层的激励函数为f1,输出层的激励函数为f2,表示隐含层中各神经元的阈值,表示输出层中各神经元的阈值。
1.2.1 信息的正向传递 输入层各神经元与隐含层各神经元之间以相应的权重连接,隐含层的第1个神经元从输入层的每个神经元处得到输出值,加权求和加上阈值通过激励函数 f1,得到该神经元的输出值为
输出层第1个神经元a1接收隐含层每个神经元输出值,并加权求和得加上阈值通过激励函数f2,得到输出层该神经元的输出值为
1.2.2 误差的反向传播 N个数据样本进入输入层正向传播,经过隐含层各神经元处理,传向输出层,得到实际输出值A,将实际输出值A与期望输出值T进行误差分析,比较并计算实际输出与期望输出的均方误差
如果MSE未达到精度要求ε,则进入反向传播过程,把均方误差信号MSE以梯度形式,按原来正向传递的通路逐层进行反向传播,并将误差信号MSE分摊给各层的所有神经元,从而获得各层神经元的误差信号MSEj(j=1,2,3),将此误差信号MSEj作为修正各连接权值和阈值的依据,并对其修改。
重复进行网络信息的正向传递和网络误差的反向传播过程,直至均方误差MSE达到精度要求或者训练达到最大迭代次数。
BP神经网络在实际应用中存在一些缺陷[10],其中在中药分析领域有 2个较明显的缺陷:第一,BP神经网络的建模过程必须构造一定的隐含层结构,但尚无合适的方法确定隐含层的神经元数,而隐含层神经元数过少或过多都会造成模型预测结果不准确;第二,BP神经网络的初始权值和阈值是随机产生的,权值和阈值的取值情况又决定着数据拟合的效果,因此该模型具有不稳定性。
2 改进的BP神经网络模型
2.1 隐含层神经元数
利用区间估算方法快速确定BP神经网络隐含层神经元数。具有单隐层的BP神经网络模型能够映射所有连续函数,在不约束隐含层神经元数的情况下,单隐层的BP神经网络模型能够实现任意的非线性映射[11]。因此,本研究选用单隐层模型。
隐含层神经元数的确定是BP神经网络模型中非常关键和复杂的问题,目前尚无标准方法来确定最佳隐含层神经元数。如果隐含层神经元数过少,会使得BP神经网络性能不佳,不能产生足够的连接权组合来满足网络对样本的学习需求;如果隐含层神经元数过多,极易陷入局部最小值,达不到最优点,出现过拟合现象[12]。许多学者通过试凑法[13-15]归纳出了确定隐含层神经元数目的一些经验性公式,如其中 k为隐含层神经元数目,n为输入层神经元数目,m为输出层神经元数目,a为常数(一般a∈[1,10])。
实践表明,最佳隐含层神经元数常介于2logk n=和之间,因此本研究采用区间估算来快速确定BP神经网络隐含层神经元数的方法。具体步骤:①构建一个单隐层的BP神经网络结构,网络输入层神经元数目为n,输出层神经元数目为m,初始隐含层神经元数目;②初始化 BP神经网络,通过权值直接确定法[16]设置网络各层的连接权值、阈值,并设置精度要求ε;③网络训练,计算均方误差MSE;④若隐含层增加 1个神经元数目,返回步骤③,否则停止运算;⑤比较不同隐含层神经元数下的网络均方误差,选择最小均方误差所对应的隐含层神经元数作为最佳隐含层神经元数。
2.2 初始权值和阈值
针对BP神经网络存在的“网络初始权值和阈值随机性”问题,本研究采用遗传算法来优化BP神经网络的初始权值和阈值。遗传算法[17-18]是模拟达尔文的遗传选择和自然淘汰的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。遗传算法从1组随机产生的初始解(称为群体)开始搜索过程。群体中的每个个体都是问题的1个解,称为染色体;染色体在后续迭代中不断进化,生成下一代染色体。染色体的优劣通过适应度函数衡量。根据适应度的大小从上一代和后代中选择一定数量的个体作为下一代群体继续进化,直至发现最好的染色体,即问题的最优解。
遗传算法的目标是寻找所有进化代中能够使网络均方误差最小的网络权重,但由于遗传算法只能朝着使适应度函数值增大的方向进行,所以本研究采用均方误差的倒数作为适应度函数。当该适应度函数取得最大值时,BP神经网络获得最佳权值和阈值。计算公式:式中 ()fi表示第i条染色体的适应度值;MSEi表示根据第i条染色体确定的BP神经网络权值和阈值时预测值A与期望值T的均方误差。
利用遗传算法进行BP神经网络模型权值和阈值快速寻优的具体步骤:①通过编码方式生成初始种群;②设置适应度函数;③计算群体中所有个体的适应值;④选择适应度高的个体执行遗传操作;⑤若达到终止条件,则返回最佳个体,即BP神经网络的初始权值和阈值;若未达到终止条件,则以指定的最大遗传步数为终止计算准则。基于遗传算法的BP神经网络流程图见图2。
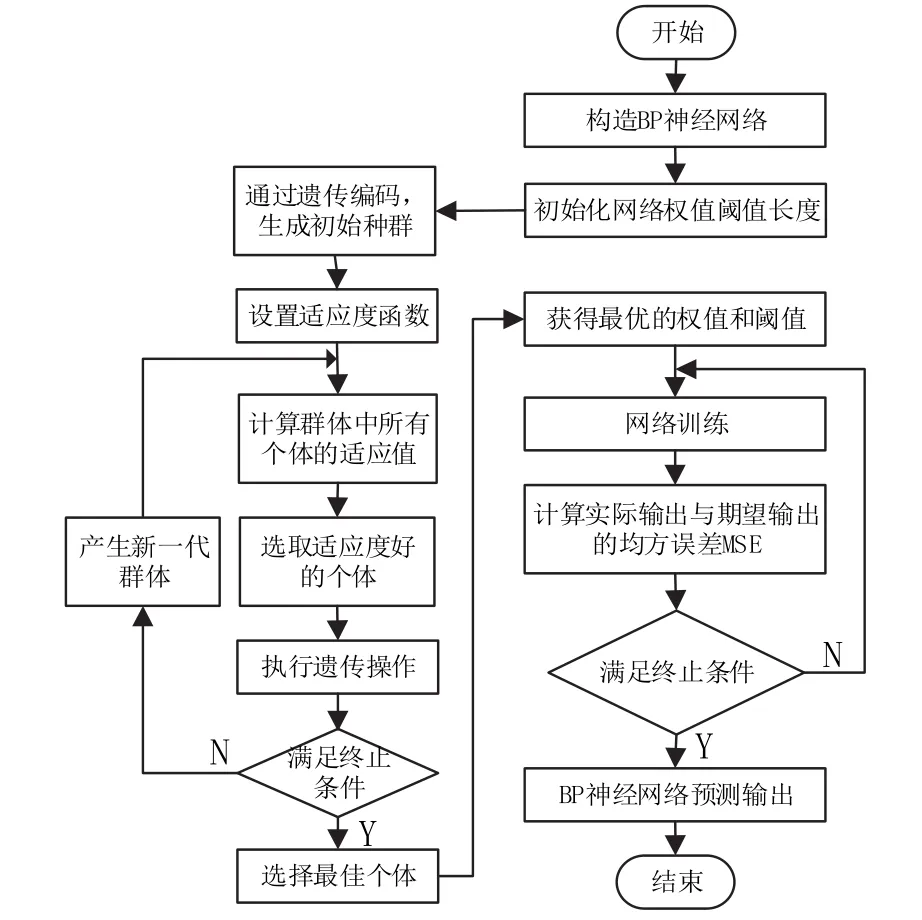
图2 基于遗传算法的BP神经网络流程图
3 中药水提液陶瓷膜膜污染预测实验
3.1 实验数据
3.1.1 参数体系 根据膜科学原理和经验规律,中药水提液中的共性高分子、物理化学性质和阻力分布等情况会对膜过程产生影响,是引起膜污染的重要因素。考虑到实际测量的可行性,选择测定5种高分子物质(固含含量、果胶含量、淀粉含量、蛋白含量和鞣质含量)、6种物化性质(pH值、电导率、盐度、浊度、黏度、密度)及3种阻力分布特征量(膜自身阻力、浓差极化阻力和表面沉积阻力),建立中药水提液膜过程参数体系。
3.1.2 数据样本 根据中药水提液膜过程参数体系,通过实验测定了207组中药水提液数据,其中145组数据(70%)作为训练集,62组数据(30%)作为测试集。
本实验目的为通过对中药水提液的共性高分子含量、物化性质和阻力分布特征量的分析来预测膜污染度,因此输入向量为固含含量等14个属性值,输出向量为膜污染度,见表1。
3.1.3 数据归一化 由于输入向量的数量级相差较大,直接将原始数据输入BP神经网络进行网络训练将使网络性能和收敛性较差,因此需要对输入向量进行归一化处理,把数据限定在区间[0,1]。而输出向量的数值符合该区间,故无需进行归一化处理。数据归一化处理公式:X=(X0-Xmin)/(Xmax-Xmin)。其中X为归一化后的数值,X0为归一化前的原始数据,Xmax和 Xmin分别为该属性原始数据的最大值和最小值。

表1 中药水提液陶瓷膜数据样本
3.2 预测模型
3.2.1 网络结构设计 根据BP神经网络原理,构建单隐层的网络模型。由于输入向量有14个属性元素,输出向量是1个属性元素,故设置网络输入层的神经元数为14,网络输出层的神经元数为1。采用“2.1”项网络隐含层神经元数的快速确定方法,估算出隐含层神经元数目区间为3~13。为了确定最佳隐含层神经元数目,设计对比实验比较不同神经元数目的网络误差,实验伪代码见图3,其中P、T、S、O分别为训练输入值、训练目标值、预测输入值和预测目标值。实验结果见表2。

图3 中药水提液陶瓷膜膜污染预测实验伪代码
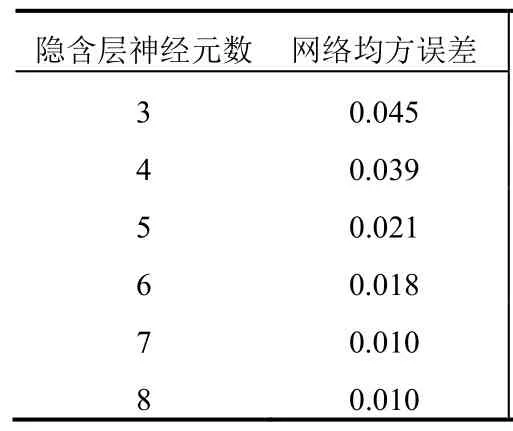
表2 隐含层神经元数目对网络均方误差的影响
表2表明,在其他条件相同的情况下,模型的隐含层神经元数目设置为9时,网络均方误差最小,模型的预测效果最佳,即最佳网络结构为14∶9∶1。
根据遗传算法原理设计优化模型。遗传算法的编码采用实数编码,编码串由4个部分组成:输入层与隐含层的连接权值、隐含层与输出层的连接权值、隐含层阈值和输出层阈值。设定种群初始规模为50,最大遗传代数为100,交叉操作采用单点交叉,变异操作采用均匀变异,交叉因子为0.6,变异因子为0.3。
3.2.2 预测结果分析 根据BP神经网络训练特点,设置网络结构的训练参数:BP神经网络的隐含层神经元激励函数采用S型正切函数,输出层神经元激励函数采用S型对数函数。应用模型进行网络训练和测试,具体预测结果见表3。 隐含层神经元数 网络均方误差 9 0.008 10 0.009 11 0.015 12 0.018 13 0.017
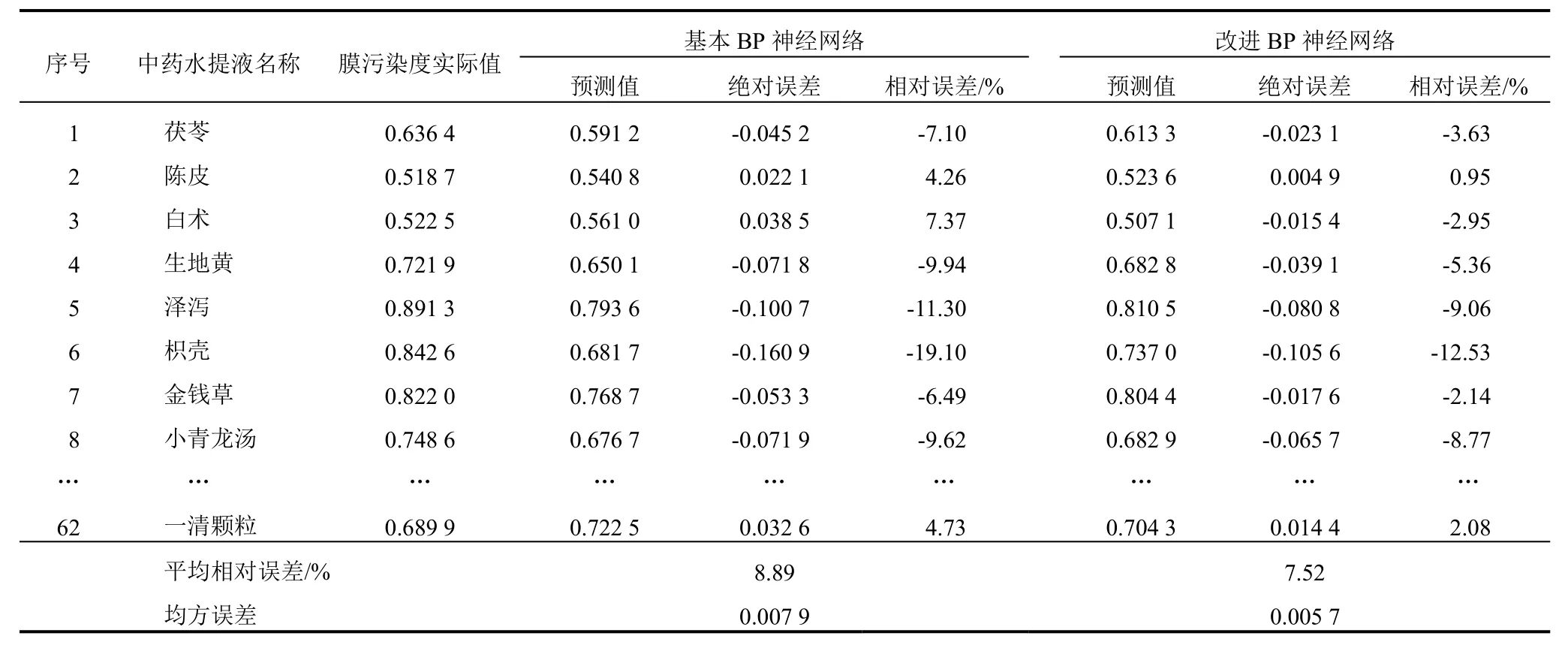
表3 中药水提液陶瓷膜膜污染BP神经网络模型预测实验结果
实验均方误差仅为0.005 7,表明基于改进BP神经网络的中药水提液陶瓷膜膜污染预测模型能够有效地对膜污染度进行预测。也证明中药水提液中的共性高分子、物理化学性质和阻力分布特征确实是影响膜污染的重要因素。
为分析模型的精度,将本研究实验结果与近年来中药水提液膜污染数据建模相关文献[19-21]进行对比,见表4。结果表明,与多元回归分析、基本BP神经网络和RBF神经网络比较,改进BP神经网络具有更好的泛化能力,拟合效果和预测精度均有较大提高。

表4 不同算法中药水提液膜污染模型预测结果比较
3.2.3 模型性能评价 由于 BP神经网络的初始权值和阈值是随机产生的,网络模型性能与其相关,也是随机变化的,因此为了对模型进行评价,令基本BP神经网络模型和改进模型均随机运行20次,分别考察达到预设目标的情况。设定平均相对误差为10%,即均方误差MSE为0.01,进行对比分析,见表5。

表5 改进算法的BP神经网络模型稳定性比较
表5表明,改进的BP神经网络稳定性更佳,说明改进算法实现了结构、权值和阈值的同步优化,避免了BP神经网络初始化的随机性和盲目性,提高了计算精度和效率。
4 小结
本研究表明,基于改进BP神经网络的中药水提液陶瓷膜膜污染预测模型能够适应中药水提液陶瓷膜纯化过程中采集到的多维、非线性数据,能够稳定准确地预测膜污染度,为中药水提液陶瓷膜膜污染的预测和防治提供了有效方法。
[1] SISKENS C A M. Fundamental of inorganic membrane science and technology[M]. Holland:Elsevier Science B V,1996:619-639.
[2] 刘忠洲,续曙光,李锁定.微滤超滤过程中的膜污染与清洗[J].水处理技术,1997(4):3-9.
[3] 樊文玲,郭立玮,林瑛.不同预处理方法对陶瓷膜澄清中药水提液过程的影响研究[J].中成药,2008,30(11):1709-1710.
[4] 贺立中.药液超滤过程中的膜污染及其防治[J].膜科学与技术,2000, 20(5):49-54.
[5] 刘春艳,凌建春,寇林元,等.GA-BP神经网络与BP神经网络性能比较[J].中国卫生统计,2013,30(2):173-176.
[6] HOLLAND J H. Adaptation in natural and artificial systems:an introductory analysis with applications to biology,control, and artificial intelligence[M]. Cambridge:MIT Press,1992:89.
[7] 王元章,吴春华,周笛青,等.基于 BP神经网络的光伏阵列故障诊断研究[J].电力系统保护与控制,2013(16):108-114.
[8] 张国翊,胡铮.改进 BP神经网络模型及其稳定性分析[J].中南大学学报:自然科学版,2011,42(1):115-124.
[9] 郝晓弘,段晓燕,李恒杰.基于BP神经网络的迭代学习初始控制策略研究[J].计算机应用,2009,29(4):1025-1027,1031.
[10] 夏玫,陈立潮,王新波.一种提高BP神经网络泛化能力的改进算法[J].计算机技术与发展,2009,19(9):62-64,68.
[11] CHEN T, CHEN H, LIU R W. Approximation capability in C(Rn) by multilayer feedforward networks and related problems[J].IEEE Transactions on Neural Network,1995,6(1):25-30
[12] 范佳妮,王振雷,钱锋.BP人工神经网络隐层结构设计的研究进展[J].控制工程,2005,12(S1):109-113.
[13] 沈花玉,王兆霞,高成耀,等.BP神经网络隐含层单元数的确定[J].天津理工大学学报,2008,24(5):13-15.
[14] 褚辉,赖惠成.一种改进的BP神经网络算法及其应用[J].计算机仿真,2007,24(4):75-77.
[15] 张庆庆,贺兴时.BP神经网络结点数选取的改进方法及其应用[J].西安工程大学学报,2008,22(4):502-505.
[16] 张雨浓,李巍,蔡炳煌,等.切比雪夫正交基神经网络的权值直接确定法[J].计算机仿真,2009,26(1):157-161.
[17] 范青武,王普,高学金.一种基于有向交叉的遗传算法[J].控制与决策,2009,24(4):542-546.
[18] 庄健,杨清宇,杜海峰,等.一种高效的复杂系统遗传算法[J].软件学报,2010,21(11):2790-2801.
[19] 洪弘.数据挖掘技术在中药水提液膜分离中的应用研究[D].南京:南京中医药大学,2012.
[20] 郭立玮,付廷明,李玲娟.面向中药复杂体系的陶瓷膜污染机理研究思路与方法[J].膜科学与技术,2009,29(1):1-7.
[21] 李玲娟,郭立玮.基于特征提取的中药水提液膜分离预测系统[J].计算机工程与设计,2010,31(9):2023-2026.
Study on Forecasting Ceramic Membrane Fouling in TCM Extracts Based on Improved BP Neural Network
DOU Peng-wei, WANG Zhen, SHE Kan-kan, FAN Wen-ling (Institute of Information Technology, Nanjing University of Chinese Medicine, Nanjing 210023, China)
ObjectiveTo prevent and treat of ceramic membrane purification of membrane fouling process of TCM extracts; To explore new methods of forecasting membrane fouling degree.MethodsBP neural network model was improved. Methods to fast determine the optimal number of neurons in the hidden layer and fast algorithm for optimizing the weight and threshold of BP neural network were studied. Data of 207 groups of TCM extracts were under network training and prediction.ResultsCompared with the models of multiple regression analysis, basic BP neural network and RBF neural network, the error of the improved BP neural network model was less than that of the BP neural network model, and the mean square error was only 0.005 7. In addition, the improved BP neural network model performance was more stable. In the 20 random running experiments, the goal of the success rate achieved up to 95%.ConclusionThe improved model has a good network performance, the fitting effect and prediction ability, and can forecast the fouling degree of membrane stably and accurately.
TCM extracts; membrane fouling; BP neural network; hidden layer neuron; genetic algorithm
10.3969/j.issn.1005-5304.2017.04.023
R2-05;R284.2
A
1005-5304(2017)04-0092-05
2016-05-23)
(
2016-06-13;编辑:向宇雁)
国家自然科学基金(81274095);江苏省科技厅自然科学基金青年项目(BK20140958);江苏省高校自然科学基金(14KJB520032)
王珍,E-mail:wznjutcm@126.com

