基于随机森林算法的参考作物蒸发蒸腾量模拟计算

王 升 付智勇 陈洪松 丁亚丽 吴丽萍 王克林

(中国科学院亚热带农业生态研究所， 长沙 410125)

基于随机森林算法的参考作物蒸发蒸腾量模拟计算

王 升 付智勇 陈洪松 丁亚丽 吴丽萍 王克林

(中国科学院亚热带农业生态研究所， 长沙 410125)

选取西南喀斯特地区4个气象站点(都安、河池、百色和融安)5 a(2008—2012年)的逐日气象数据，包括日最高气温Tmax、日最低气温Tmin、相对湿度RH、日照时数n和风速u2这5个气象因子的不同组合作为输入，并以FAO 56 Penman-Monteith法(FAO P-M)的计算结果作为标准值，建立基于随机森林(Random forest, RF)算法和基因表达式编程(Gene expression programming, GEP)算法的ET0模型，并将模拟结果与传统Hargreaves模型的计算结果进行比较。结果表明，不同气象因子组合下建立的RF模型均能较好地反映气象因子与ET0之间的非线性关系。随着气象因子的增加，RF模型模拟的精度随之提高。在仅有气温数据时，RF模型仍具有足够的精度(R2为0.875，RMSE为0.546 mm/d)，与传统Hargreaves模型相比R2平均增加了1.98%，RMSE平均减小了22.88%，因此在仅有气温数据时可用RF模型代替Hargreaves模型。RF算法对气象因子的重要性评估表明，在该区域对ET0最重要的气象因子依次为Tmax、n、Tmin、Ra、RH和u2。相同气象因子输入下，RF模型精度高于GEP模型。

参考作物蒸发蒸腾量； 随机森林； 基因表达式编程； Penman-Monteith模型； 西南喀斯特地区

引言

参考作物蒸发蒸腾量(Reference evapotranspiration,ET0)是表征大气蒸散发能力的因子，主要用于计算作物需水量，也是灌溉制度设计、水资源管理、流域水量平衡研究关键参数[1]。目前，ET0计算的标准方法是世界粮食和农业组织(FAO)推荐采用的的FAO 56 Penman-Monteith模型(以下简称FAO P-M)，该模型综合了辐射项和空气动力学项，具有充分的理论基础，已经在世界各地、各种气候类型下通过蒸渗仪进行了验证，它也常被应用于校准其他ET0模型的参数[1-2]。然而FAO P-M 需要较为完备的气象数据(太阳辐射、气温、风速和相对湿度)，即使在发达国家能同时测量这些气象数据的气象站点也很有限，而且其对数据质量有严格的要求，所以它的应用受到一定限制[3]。其他需要较少气象参数的传统ET0经验/半经验模型(蒸发皿法、基于温度或辐射的方法等)准确度较低，如DJAMAN等[4]评估了16种ET0模型，发现这些方法高估或低估了ET0，因此在使用时需要根据具体研究区进行参数校正[5]。发展利用较少气象因子得到足够精度ET0的模型仍然是一个值得研究的课题。

近年来随着计算能力的大幅提高和大数据时代的崛起，各种机器学习方法被广泛应用于多个领域[6]，也被应用于ET0模拟计算，为资料缺乏地区ET0计算提供了新途径。如人工神经网络(Artificial neural network，ANN)[7]，然而ANN容易过拟合且收敛速度慢。SHIRI等[2]研究表明基因表达式编程算法(GEP)的ET0模拟结果优于自适应模糊推理系统(ANFIS)、Priestley-Taylor法和Hargreaves法。WEN等[8]和侯志强等[9]研究了支持向量机(SVM)模拟ET0，冯禹等[10]用极限学习机模拟川中丘陵区ET0，均取得较好的效果。FDRNANDEZ-DELGADO等[11]评估了179种机器学习算法在121个数据集上的性能，结果表明随机森林(Random forest, RF)算法的性能最好，其次是SVM(采用高斯核函数)。随机森林是一种组合式机器学习方法，其通过对大量分类树的汇总提高了模型的预测精度，因其具有更高的准确性和稳健性而在各行业得到越来越多的应用[12]，如用于构建小麦叶片叶绿素相对含量的遥感反演模型[13]、苹果树冠叶面积指数估测模型[14]等。而目前应用随机森林算法模拟ET0的研究较少。

中国西南喀斯特地区由于特殊的地质背景和强烈的岩溶作用，以及近代人类不合理的土地开发利用，导致植被退化、水土流失严重，石漠化不断加剧[15-16]。尽管该地区降雨充沛(年平均降水量大于1 200 mm)，但由于地表地下的二元结构发育，土层浅薄且不连续，土壤入渗能力强，使得土壤储水能力低[17]。且喀斯特系统普遍存在溶洞、溶沟、溶隙、漏斗和落水洞，使得该地区水文过程变化迅速，地表水漏失严重，形成了喀斯特小生境特殊的岩溶干旱现象，因此水分亏缺依然是西南喀斯特石漠化地区植被恢复和重建的主要限制性因子[18]。在全球气候变化大背景下，近60 a来该地区降水量呈下降趋势(-1.14 mm/a)，极端气候事件频繁[19]。准确估算该地区ET0有助于指导制定植被恢复策略以及合理开发利用水资源。因此，本文使用桂西北喀斯特地区4个气象站点5 a(2008—2012年)的逐日气象数据，采用不同的气象因子组合，以FAO P-M法的结果为标准，比较基于RF、GEP算法的ET0模型以及传统Hargreaves模型对ET0的模拟效果，旨在探讨随机森林算法模拟计算ET0的可行性，以期获得使用较少气象参数而计算精度接近于FAO P-M且高于传统经验公式的ET0模型，为该区域植被恢复重建和农业用水管理提供科学依据。

1 材料与方法

1.1 数据来源

气象数据来自桂西北喀斯特地区的4个气象站点：百色、都安、河池和融安，气象要素包括：日最高气温Tmax、日最低气温Tmin、相对湿度RH、日照时数n和2 m高度处风速u2的5 a逐日数据(2008—2012年)，如表1所示。因为ET0与其他气候因素相比变化程度较小，由5 a的逐日ET0对ET0模型进行建立及检验是可接受的[2]。

表1 气象站点位置及气象因素平均值Tab.1 Weather station locations and climatic data averages

1.2 参考作物腾发量计算模型

1.2.1 FAO P-M模型

FAO P-M模型是计算ET0的标准方法[1]，其表达式为

(1)

式中Rn——太阳净辐射通量，MJ/(m2·d)G——土壤热通量，MJ/(m2·d)Δ——饱和水汽压-温度曲线的斜率，kPa/℃γ——湿度计常数，kPa/℃es——饱和水汽压，kPaea——实际水汽压，kPaT——2 m高度处的平均气温，℃

1.2.2 Hargreaves模型

Hargreaves模型仅需要日最低和最高气温，其表达式为

(2)

式中Ra——大气顶层太阳辐射，由气象站点纬度及日序数算得[20]，mm/d

1.3 随机森林模型概述

RF是由BREIMAN等[21]在2001年提出的一种集成学习算法，具有需要调整的参数较少、不易过拟合、能有效处理大数据集并且可以给出变量的重要性估计等特点[12]。RF通过多次bootstrap抽样获得多个随机样本，然后使用这些样本建立相对应的决策树，从而构成随机森林用于分类和回归分析。对于回归问题，则是由这些树的结果的平均值得到因变量的预测值。用RF算法进行回归模拟有2个参数需要确定：每个树节点随机变量的数量(mtry)和森林中树的数量(ntree)。假定原始数据有m个变量，对于回归问题，通常取mtry=m/3。随着随机森林中决策树的数量的增加，森林的总误差率会趋向一个稳定的有限上界，YANG等[22]发现ntree的默认取值(500)不足以产生稳定的结果，因此本文取ntree=2 000。

RF模型判定变量重要性的方法是在每一棵决策树的变量中加入随机噪声，然后检验袋外误差的增减，如果误差增加，则该变量比较重要，反之则不重要[25]。计算方法为

(3)

式中IVIMi——变量i的重要性EerrOOB1——袋外数据(Out of bag，OOB)误差EerrOOB2——随机对袋外数据OOB所有样本的变量i加入噪声干扰，再次计算的袋外误差

1.4 基因表达式编程算法概述

关于基因表达式编程算法结构及其模拟计算ET0过程详见文献[3]。

1.5 评价指标

采用2个评价指标，即决定系数R2和均方根误差RMSE。其计算式分别为

(4)

(5)

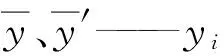
2 结果与分析

将4个站点5 a的气象数据分为2部分，其中2008—2010年的日气象资料及FAO P-M模型计算的ET0为训练样本，用2011—2012年的日气象资料及FAO P-M模型计算的ET0为检验样本，分别采用RF和GEP算法，得到不同气象因子组合下的ET0模型。4个气象因子(气温、风速、相对湿度和日照时数)中，气温是各个气象站的常规观测项目，而相对湿度、风速和日照时数只有较少的站点能同时观测[23]。因此气温(Tmax和Tmin)应用于所有输入组合中。基于15个气象因子组合方案，分别建立15个基于RF和GEP算法的模型，输入的气象因子组合及模型精度如表2、3所示。

2.1 检验期不同气象因子输入组合下RF模型计算结果对比

由表2可见(Har表示Hargreaves模型)，4个站点R2的变化范围为0.809～0.991，RMSE的变化范围为0.168～0.678 mm/d。RF1为随机森林温度模型，其输入因子仅为Tmax和Tmin，能够达到足够精度，R2平均值为0.842，RMSE平均值为0.603 mm/d。与传统Hargreaves模型相比(R2=0.858，RMSE=0.708 mm/d)，精度差异不大，而且从RMSE角度来看，RF1的精度高于传统Hargreaves模型。

TRAORE等[24]研究表明仅利用气温数据不足以得到足够准确的ET0计算结果，增加额外的气象因子能够提高计算精度。因此，RF2、RF3和RF4分别在RF1的基础上引入RH、u2和n，与RF1相比，其精度均有所提高，其中引入日照时数的RF4提高最显著，R2平均值由0.842增加到0.921，RMSE的平均值由0.603 mm/d降低到0.437 mm/d。其次为引入相对湿度的RF2模型(平均R2=0.908，平均RMSE=0.460 mm/d)，引入风速的RF3精度提升最小(平均R2=0.884，平均RMSE=0.520 mm/d)。这说明不同气象因子对ET0的重要性不同，桂西北喀斯特地区ET0除了气温变量，受n的影响最大，其次为RH和u2。RF模型可以给出输入变量的重要性估计，可帮助理解主要影响因变量的变量[12]。图1给出了6个变量重要性排序，4个站点气象因子相对重要性依次为：Tmax、n、Tmin、Ra、RH和u2，结果与模型RF2、RF3和RF4的平均精度表现一致。

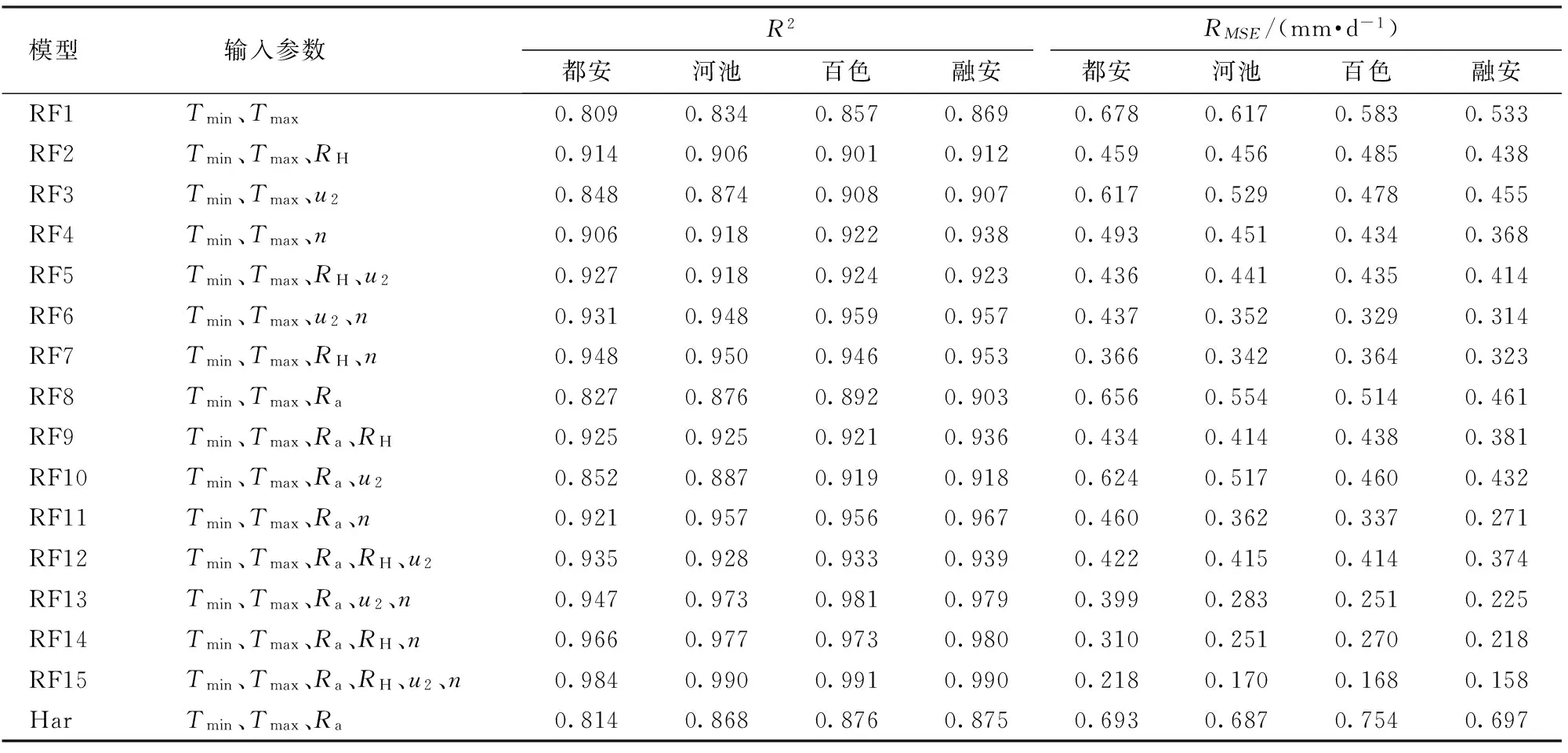
表2 不同气象因子组合下验证期RF模型精度Tab.2 Statistical performance of RF models and Hargreaves model during test period

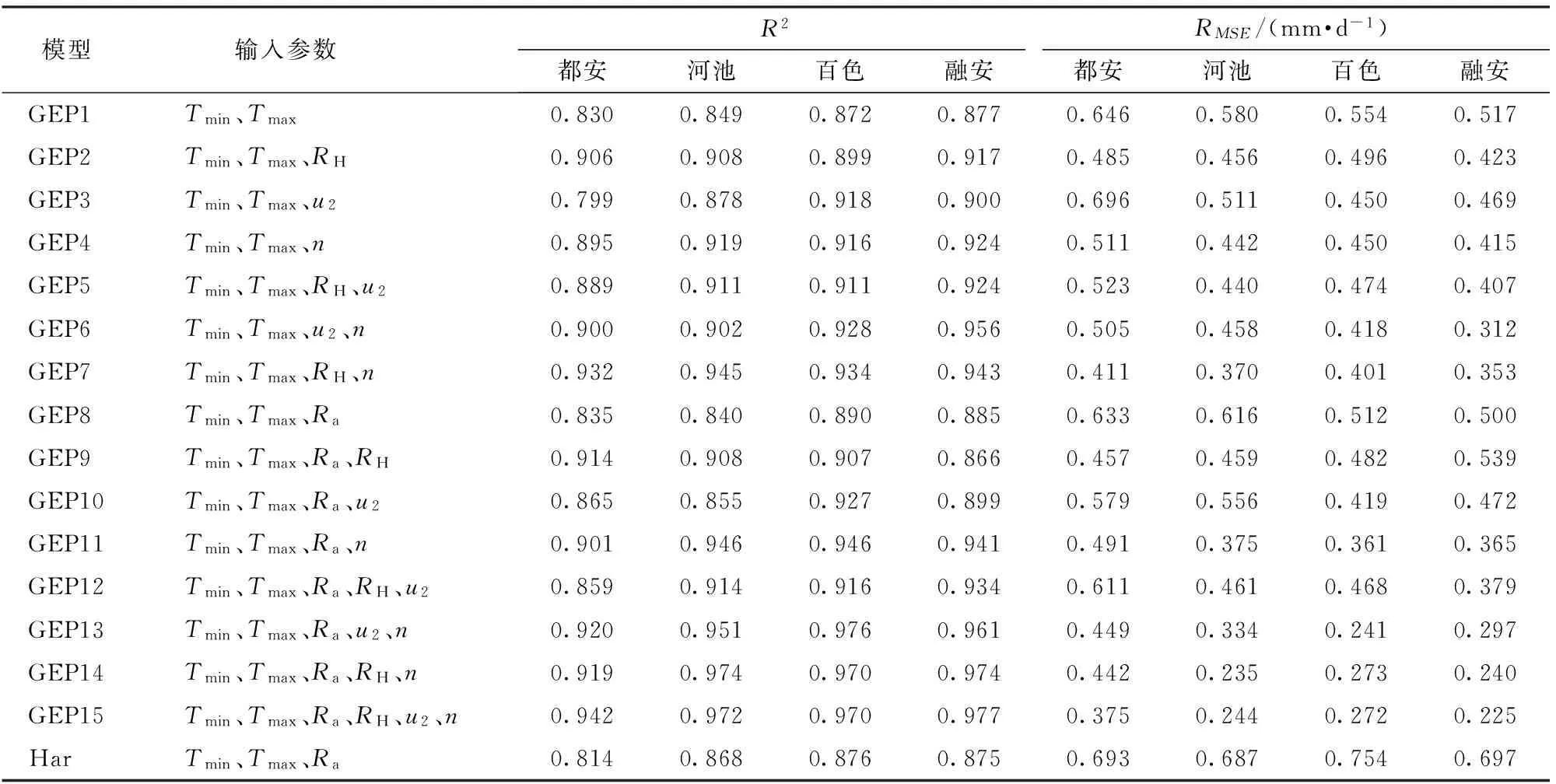
表3 不同气象因子组合下验证期GEP模型精度Tab.3 Statistical performance of GEP models and Hargreaves model during test period

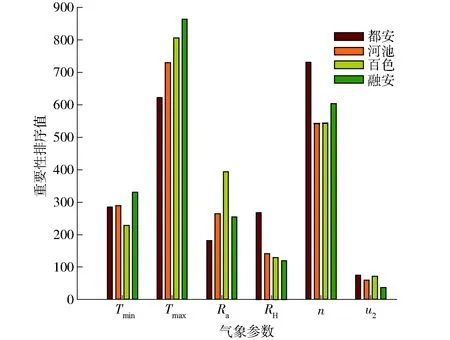
图1 影响ET0的气象因子重要性排序Fig.1 Rank of importance of meteorological variables influencing ET0

模型RF5、RF6和RF7分别在模型RF2、RF3和RF4的基础上引入u2、n和RH得到，精度均得到提高，平均R2分别增加了1.65%、7.35%和3.04%，平均RMSE分别减小了6.09%、31.15%和20.14%。RF7模型(平均R2=0.949，平均RMSE=0.349 mm/d)的精度明显高于RF6(平均R2=0.949，平均RMSE=0.358 mm/d)和RF5(平均R2=0.923，平均RMSE=0.432 mm/d)，这也可以由气象因子的重要性来解释，重要性依次为RH+n、n+u2和RH+u2。

模型RF8～RF14分别在模型RF1～RF7的基础上引入Ra得到，由表2可见模型精度均显著提高，平均R2分别增加了3.92%、2.09%、1.13%、3.15%、1.19%、2.21%和2.63%，平均RMSE分别减小了9.45%、9.35%、2.31%、18.08%、6.02%、18.99%和24.93%。这是因为蒸散发的能量来源为太阳辐射，理论太阳辐射由日地相对距离和太阳高度角决定，日地相对距离是日序数的函数，太阳高度角是地理纬度的函数，而大气顶层太阳辐射Ra是地理纬度和日序数的函数，综合反映了这2个因素，因此引入Ra可提高ET0模型的精度[3]。而且Ra不需要观测，由计算得到，避免了观测导致的误差。我国目前大多数气象站点未能观测太阳辐射数据，只能由n转换得到，因此在缺少太阳辐射值而用日照时数来计算太阳净辐射时，有必要引入Ra。

模型RF8的输入因子(Tmax、Tmin和Ra)和传统Hargreaves模型相同，4个站点RF8模型的精度均高于Hargreaves模型，平均R2增加了1.98%，平均RMSE减小了22.88%，因此在仅有气温数据时，可以使用RF模型代替传统Hargreaves模型，以提高ET0计算精度。

模型RF15使用了与FAO P-M相同的所有气象因子，其模拟结果也是最准确的(平均R2=0.989，平均RMSE=0.179 mm/d)。尽管RF15的输入因子与FAO P-M相同，但结果仍然有差异，所需气象因子完备情况下并不能替代FAO P-M模型，这是由于FAO P-M包含了辐射项和空气动力学项，每一项的中间参数都由气象因子、地理位置信息、仪器安装高度以及日序数等得到，计算过程会引入误差，而RF算法未能捕捉到这些误差，造成了2种模型的计算差异。

2.2 检验期不同气象因子输入组合下GEP模型计算结果对比

表3给出了不同气象因子组合下基于GEP算法的ET0模型精度，可见GEP模型能够很好地模拟ET0和气象因子之间的非线性关系，4个站点平均R2的变化范围为0.857～0.965，平均RMSE的变化范围为0.279～0.574 mm/d。比较GEP1、GEP2、GEP3和GEP4，可见与RF模型相同，引入n的GEP4模型精度高于引入RH和u2的GEP2和GEP3模型。同样，在模型GEP2、GEP3和GEP4的基础上引入u2、n和RH得到的GEP5、GEP6和GEP7模型的精度也明显提高，平均R2分别增加了0.11%、5.49%和2.74%，平均RMSE分别减小了0.86%、20.49%和15.60%。比较GEP8～GEP14与GEP1～GEP7，可见与RF模型一样，引入Ra使得模型精度均显著提高。

GEP8模型和传统Hargreaves模型使用的气象因子相同，在4个站点GEP8模型的精度均优于Hargreaves模型，平均R2提高了0.58%，平均RMSE减小了20.20%。相比于其他算法产生的是黑箱模型，GEP算法的一个优点是能够生成明确的代数表达式，便于应用。因此在仅有气温，缺乏其他气象资料时，GEP8模型可以代替Hargreaves模型。生成4个站点(都安、河池、百色和融安)3个参数(Tmin、Tmax、Ra)GEP模型表达式分别为

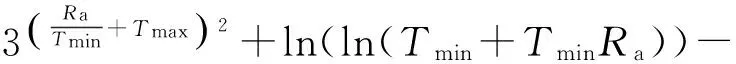
(6)

(7)

(8)

(9)

2.3 RF和GEP模型对比

比较表2、3可见，除了输入组合1(Tmax和Tmin)和输入组合10(Tmin、Tmax、Ra和u2)产生的RF模型计算精度低于GEP模型外，其他输入组合下RF模型精度均高于相应GEP模型,平均RMSE分别减小了1.20%、2.26%、4.12%、6.84%、18.23%、10.04%、3.48%、16.20%、11.33%和56.30%。图2给出了检验期(2011—2012年)RF8、RF11和RF15以及GEP8、GEP11和GEP15模型模拟结果与FAO P-M计算结果的散点图，根据线性回归R2以及数据点分散程度可见，RF8、RF11和RF15模型精度要高于相应GEP8、GEP11和GEP15模型，与表2和表3统计结果一致。尽管GEP算法产生的模型达到足够精度所需的运算时间远大于RF算法，但GEP模型能够产生自变量和因变量之间的算术表达式，这一方面便于挖掘自变量和因变量之间的理论关系，另一方面也便于应用。

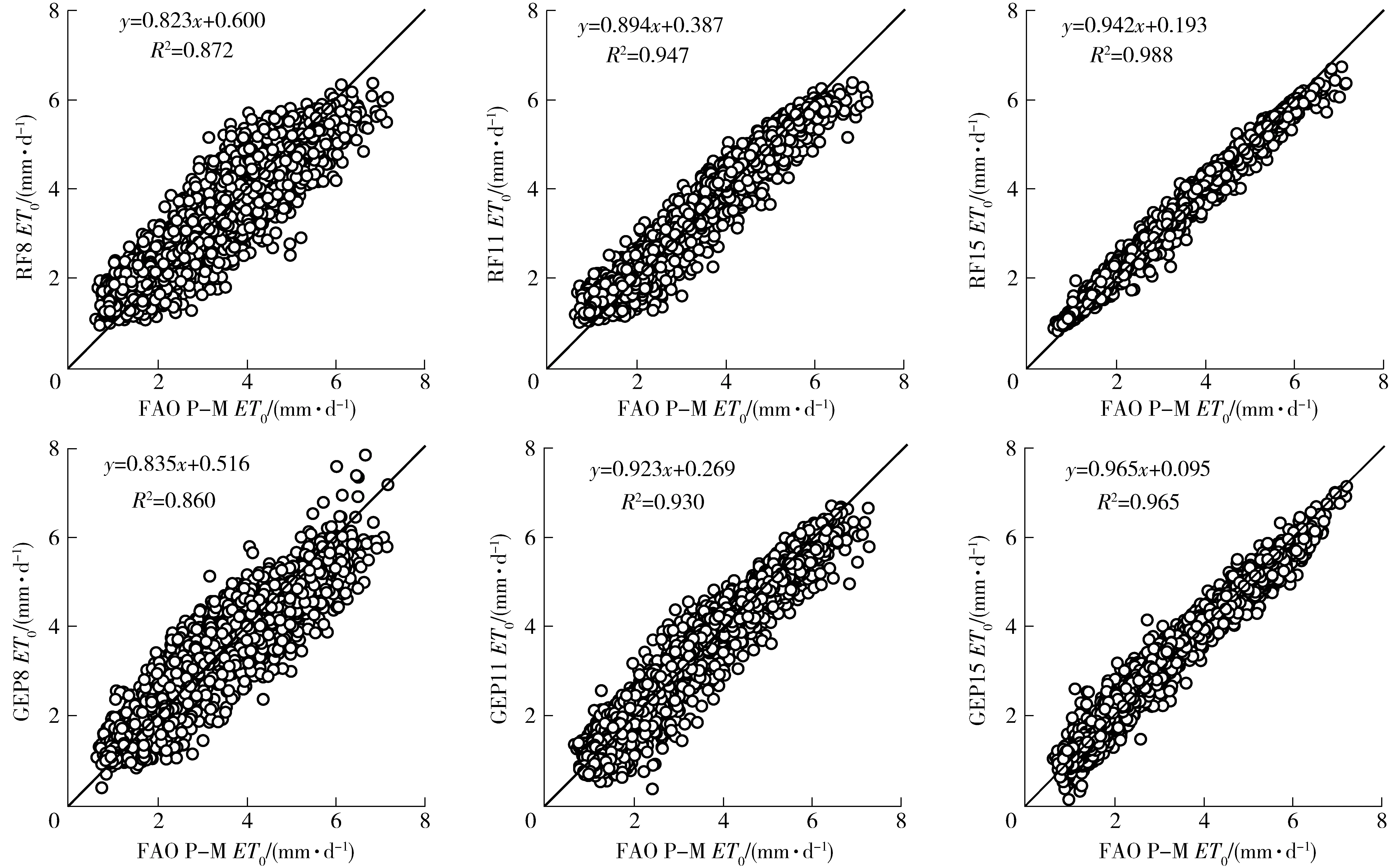
图2 检验期RF8、RF11、RF15和GEP8、GEP11、GEP15模型结果与FAO P-M结果比较的散点图Fig.2 Comparative scatter plots between ET0 of RF8, RF11, RF15, GEP8, GEP11, GEP15 and ET0 from FAO P-M during test period

3 讨论

我国西南喀斯特生态脆弱区二元结构发育，雨水通过地表漏斗进入地下暗河，加之土层浅薄，水分涵养能力差，因此尽管降水较丰富，但主要埋藏于地下，地表耕地易于干涸而出现旱情[15,17]。随着社会经济的发展，工业用水比例增加，相应农业可用水量减小，因此精确计算ET0有助于合理分配和管理利用有限的农业水资源。然而在大多数地区气象站所观测的气象数据并不满足FAO P-M模型的要求(关键气象因子缺失、数据质量不可靠等)，如内蒙古自治区118个气象站中能观测太阳净辐射数据的仅有7个，贵州省80个气象站中仅有1个能观测该数据，且仅有19个站点能观测用于计算太阳净辐射的日照时数[26]，因此有必要研究基于机器学习算法建立所需气象因子少、精度足够高的ET0计算模型。由于随机森林算法在不同数据集上表现稳健、预测准确性高、所需用户指定参数少、不容易过拟合且能够计算预测因子的重要性，因此它在很多领域得到应用[6,11-13]。本研究首次探讨了随机森林回归算法在ET0计算方面的能力，发现在相同输入下，其计算精度明显高于GEP模型和径向基函数神经网络模型[3]，其中RF8仅利用最大和最小气温而模型精度高于相同输入因子的传统Hargreaves模型，证明了随机森林算法计算ET0的可行性，为后续研究建立该区基于随机森林的通用ET0模型奠定了基础。以峰丛洼(谷)地为基本景观单元的西南喀斯特地貌“十里不同天”，气象因子(降水量、温度、湿度和光照)时空变异大，然而不可能针对每个灌区建立气象站，这种情况下使用基于简单易测的气象因子的ET0模型(如本文建立的基于气温的RF8模型)，既能满足生产需求，又能达到节水的目的。

随机森林算法的另一个优良特征是能计算自变量对因变量的重要性，因此其结果可解释性强于其他机器学习算法。具体在本研究中表现为给出各个气象因子对计算ET0的重要性程度，一方面有助于选取关键因子以提高ET0计算精度，另一方面有助于评估未来气候变化条件下农业水资源需求量的变化。

本研究所建立的不同气象站点、不同输入因子的ET0模型可能仅适应于该站点，下一步需要根据研究区更多气象站点的数据，建立适用于整个研究区的RF泛化模型。

4 结论

(1)随机森林算法成功应用于亚热带季风气候区的西南喀斯特地区ET0模拟计算，不同气象因子组合输入下建立的RF模型均能较好地反映气象因子与ET0之间的非线性关系。随着气象因子的增加，RF模型模拟的精度随之提高。在仅有气温数据时，RF模型仍具有足够的精度(R2=0.875，RMSE=0.546 mm/d)，与传统Hargreaves模型相比平均R2增加了1.98%，平均RMSE减小了22.88%，因此在仅有气温数据时可用RF模型代替Hargreaves模型。

(2)不同气象因子的引入对模型精度提升不同，在气温基础上引入日照时数对精度提升最显著(平均R2为0.921，平均RMSE为0.437 mm/d)，其次为引入相对湿度(平均R2为0.908，平均RMSE为0.460 mm/d)和风速(平均R2为0.874，平均RMSE为0.532 mm/d)。RF算法对气象因子的重要性评估表明，在该区域对ET0重要的气象因子依次为Tmax、n、Tmin、Ra、RH和u2。引入不需要观测的大气顶层太阳辐射Ra能够明显提高模型精度。

(3)总体来说，相同气象因子组合输入下，基于RF算法建立的模型精度要高于基于GEP算法建立的模型。然而GEP模型具有明确的算术表达式，因此对计算机技术并不精通的灌溉工作人员建议使用GEP模型，水资源管理及水量平衡研究中建议使用RF模型。

1 ALLEN R G, PEREIRA L S, RAES D, et al. Crop evapotranspiration—guidelines for computing crop water requirements. FAO irrigation and drainage paper 56[R]. Rome： FAO, 1998, 300(9): D5109.

2 SHIRI J, KISI Ö, LANDERAS G, et al. Daily reference evapotranspiration modeling by using genetic programming approach in the Basque Country (Northern Spain)[J]. Journal of Hydrology, 2012, 414: 302-316.

3 王升，陈洪松，聂云鹏，等. 基于基因表达式编程算法的参考作物腾发量模拟计算[J/OL]. 农业机械学报, 2015, 46(4):106-112.http:∥www.j-csam.org/jcsam/ch/reader/create_pdf.aspx?file_no=20150416&year_id=2015&quarter_id=4&falg=1. DOI:10.6041/j.issn.1000-1298.2015.04.016. WANG Sheng，CHEN Hongsong，NIE Yunpeng，et al. Simulation of evapotranspiration based on gene-expression programming method[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(4): 106-112. (in Chinese)

4 DJAMAN K, BALDE A B, SOW A, et al. Evaluation of sixteen reference evapotranspiration methods under sahelian conditions in the Senegal River Valley[J]. Journal of Hydrology: Regional Studies, 2015, 3: 139-159.

5 胡庆芳，杨大文，王银堂，等. Hargreaves公式的全局校正及适用性评价[J]. 水科学进展, 2011,22(2): 160-167. HU Qingfang，YANG Dawen，WANG Yintang，et al. Global calibration of Hargreaves equation and its applicability in China[J]. Advances in Water Science, 2011, 22(2): 160-167. (in Chinese)

6 周志华. 机器学习[M]. 北京: 清华大学出版社, 2016.

7 LANDERAS G, ORTIZ-BARREDO A, LPEZ J J. Comparison of artificial neural network models and empirical and semi-empirical equations for daily reference evapotranspiration estimation in the Basque Country (Northern Spain)[J]. Agricultural Water Management, 2008, 95(5): 553-565.

8 WEN X, SI J, HE Z, et al. Support-vector-machine-based models for modeling daily reference evapotranspiration with limited climatic data in extreme arid regions [J]. Water Resources Management, 2015, 29(9): 3195-3209.

9 侯志强，杨培岭，苏艳平，等. 基于最小二乘支持向量机的ET0模拟计算[J]. 水利学报, 2011, 42(6): 743-749. HOU Zhiqiang，YANG Peiling，SU Yanping，et al. Simulation ofET0based on LS-SVM Method[J]. Journal of Hydraulic Engineering, 2011, 42(6): 743-749. (in Chinese)

10 冯禹，崔宁博，龚道枝，等. 基于极限学习机的参考作物蒸散量预测模型[J]. 农业工程学报,2015, 31(增刊1): 153-160. FENG Yu，CUI Ningbo，GONG Daozhi，et al. Prediction model of reference crop evapotranspiration based on extreme learning machine[J]. Transactions of the CSAE, 2015, 31(Supp.1): 153-160. (in Chinese)

11 FERNANDEZ-DELGADO M, CERNADAS E, BARRO S, et al. Do we need hundreds of classifiers to solve real world classification problems?[J]. The Journal of Machine Learning Research, 2014, 15(1): 3133-3181.

12 张雷，王琳琳，张旭东，等. 随机森林算法基本思想及其在生态学中的应用——以云南松分布模拟为例[J]. 生态学报, 2014,34(3): 650-659. ZHANG Lei，WANG Linlin，ZHANG Xudong，et al. The basic principle of random forest and its applications in ecology: a case study ofPinusyunnanensis[J]. Acta Ecologica Sinica, 2014, 34(3): 650-659. (in Chinese)

13 王丽爱，马昌，周旭东，等. 基于随机森林回归算法的小麦叶片SPAD值遥感估算[J/OL]. 农业机械学报, 2015, 46(1): 259-265.http:∥www.j-csam.org/jcsam/ch/reader/create_pdf.aspx?file_no=20150136&flag=1&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2015.01.036. WANG Li’ai，MA Chang，ZHOU Xudong，et al. Estimation of wheat leaf SPAD value using RF algorithmic model and remote sensing data[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(1): 259-265. (in Chinese)

14 韩兆迎，朱西存，房贤一，等. 基于SVM与RF的苹果树冠LAI高光谱估测[J]. 光谱学与光谱分析, 2016, 36(3): 800-805. HAN Zhaoying，ZHU Xicun，FANG Xianyi，et al. Hyperspectral estimation of appple tree canopy LAI based on SVM and RF regression[J]. Spectroscopy and Spectral Analysis, 2016, 36(3): 800-805. (in Chinese)

15 陈洪松，杨静，傅伟，等. 桂西北喀斯特峰丛不同土地利用方式坡面产流产沙特征[J]. 农业工程学报, 2012, 28(16): 121-126. CHEN Hongsong，YANG Jing，FU Wei，et al. Characteristics of slope runoff and sediment yield on karst hill-slope with different land-use types in northwest Guangxi[J]. Transactions of the CSAE, 2012, 28(16): 121-126. (in Chinese)

16 JIANG Z, LIAN Y, QIN X. Rocky desertification in Southwest China: impacts, causes, and restoration[J]. Earth-Science Reviews, 2014, 132: 1-12.

17 付同刚，陈洪松，张伟，等. 喀斯特小流域土壤含水率空间异质性及其影响因素[J]. 农业工程学报, 2014, 30(14): 124-131. FU Tonggang，CHEN Hongsong，ZHANG Wei，et al. Spatial variability of soil moisture content and its influencing factors in small karst catchment during dry period[J]. Transactions of the CSAE, 2014, 30(14): 124-131. (in Chinese)

18 CHEN H, ZHANG W, WANG K, et al. Soil moisture dynamics under different land uses on karst hillslope in northwest Guangxi, China[J]. Environmental Earth Sciences, 2010, 61(6): 1105-1111.

19 LIU M, XU X, SUN A Y, et al. Is southwestern China experiencing more frequent precipitation extremes?[J]. Environmental Research Letters, 2014, 9(6): 64002.

20 刘钰，蔡林根. 参照腾发量的新定义及计算方法对比[J]. 水利学报, 1997,24(6): 27-33. LIU Yu，CAI Lin’gen. Update definition and computation of reference evapotranspiration comparison with former method[J]. Journal of Hydraulic Engineering, 1997,24(6):27-33. (in Chinese)

21 BREIMAN L. Random forests[J]. Machine Learning, 2001, 45(1): 5-32.

22 YANG R, ZHANG G, LIU F, et al. Comparison of boosted regression tree and random forest models for mapping topsoil organic carbon concentration in an alpine ecosystem[J]. Ecological Indicators, 2016, 60: 870-878.

23 DROOGERS P, ALLEN R G. Estimating reference evapotranspiration under inaccurate data conditions[J]. Irrigation and Drainage Systems, 2002, 16(1): 33-45.

24 TRAORE S, WANG Y, KERH T. Artificial neural network for modeling reference evapotranspiration complex process in Sudano-Sahelian zone[J]. Agricultural Water Management, 2010, 97(5): 707-714.

25 王茵茵，齐雁冰，陈洋，等. 基于多分辨率遥感数据与随机森林算法的土壤有机质预测研究[J]. 土壤学报, 2016, 53(2): 342-354. WANG Yinyin，QI Yanbing，CHEN Yang，et al. Prediction of soil organic matter based on multi-resolution remote sensing data and random forest algorithm[J]. Acta Pedologica Sinica, 2016, 53(2): 342-354. (in Chinese)

26 XU J. Proper methods and its calibration for estimating reference evapotranspiration using limited climatic data in Southwestern China[J]. Archives of Agronomy & Soil Science, 2014, 61(3):415-426.

Simulation of Reference Evapotranspiration Based on Random Forest Method

WANG Sheng FU Zhiyong CHEN Hongsong DING Yali WU Liping WANG Kelin

(InstituteofSubtropicalAgriculture,ChineseAcademyofSciences,Changsha410125,China)

Accurate estimation of reference evapotranspiration (ET0) is very important in hydrological cycle research, and it is also essential in agricultural water management and allocation. Using less meteorological parameters to estimateET0is necessary in areas with limited data. The ability of random forest (RF) and gene expression programming (GEP) algorithm in modelingET0was investigated and compared by using fewer meteorological parameters collected from four weather stations of Duan, Hechi, Baise and Rong’an, in karst region of southwest China, over a five-year period (2008—2012). Daily climatic data of the four stations, including maximum temperature (Tmax), minimum temperature (Tmin)，sunshine duration (n), relative humidity (RH) and wind speed (u2) were employed to modelET0by using FAO 56 Penman-Monteith equation as the reference, and their performances were evaluated using determination coefficient (R2) and root mean square error (RMSE). From the statistical results, the derived RF-based (R2was ranged from 0.809 to 0.991, andRMSEwas ranged from 0.158 mm/d to 0.678 mm/d) and GEP-based (R2was in range of 0.830～0.977, andRMSEwas in range of 0.225～0.645 mm/d)ET0models were successfully applied to modelET0with different input combinations. When only the temperature data can be used, the RF models produced satisfactory results (R2=0.875，RMSE=0.546 mm/d), which can be used as an alternative to the conventional Hargreaves model. The relative importance of meteorological variables forET0can be assessed by RF method, the order of the relative importance of meteorological variables was:Tmax,n,Tmin,Ra,RHandu2. In most cases, the RF models were found to perform better than the GEP models. The results were expected to be useful to guide rehabilitation strategies and agricultural water management in karst region of Southwest China.

reference evapotranspiration; random forest; gene-expression programming; Penman-Monteith model; karst region of Southwest China

10.6041/j.issn.1000-1298.2017.03.038

2016-07-18

2016-09-07

国家重点基础研究发展计划(973计划)项目(2015CB452703)和国家自然科学基金项目(41171187、31100294)

王升(1987—)，男，博士生，主要从事坡地水文研究，E-mail: hjdx@foxmail.com

陈洪松(1974—)，男，教授，博士生导师，主要从事生态水文研究，E-mail: hbchs@isa.ac.cn

S161.4

A

1000-1298(2017)03-0302-08