自适应车用永磁同步电机在线参数辨识

郑鲁阳 张 希(上海交通大学机械与动力工程学院, 上海 200240)

自适应车用永磁同步电机在线参数辨识

郑鲁阳 张 希
(上海交通大学机械与动力工程学院, 上海 200240)

车用永磁同步电机在运行过程中复杂的工况和恶劣的工作条件会影响电机的参数进而影响电机控制性能。本文采用自适应的参数辨识算法，对永磁同步电机参数进行在线辨识并反馈回电机控制系统，改进原有控制参数。该算法基于永磁同步电机的数学模型，根据转速电流反馈信号，借助Lyapunov稳定理论建立负载转矩和交直轴电感的辨识模型并推导其自适应律。基于MTPA算法的仿真和实验结果表明本文提出的参数辨识算法能够在较短时间内实现高效的参数辨识，且估计值与真实值的误差较小。

永磁同步电机 自适应 在线参数辨识 MTPA

永磁同步电机因其精度高、功率密度大、稳定性好以及优秀的控制性能等特点越来越广泛地应用于电动汽车领域。永磁同步电机的控制算法中，传统的电流环、速度换双闭环反馈PI控制策略是根据恒定的电机参数设计的，在运行情况稳定、外部干扰较弱的情况下拥有良好的控制性能。而电动汽车复杂的运行工况、恶劣的运行环境会导致电机的参数发生变化，传统PI控制难以保持其控制性能，为了保证控制性能，在线实时地辨识电机参数，并反馈回电机控制系统改进控制参数具有重要意义。

针对在线参数辨识，国内外许多学者做出了研究。其中[1]-[3]采用模型参考自适应算法辨识电机参数。该算法简便易行，但对于负载转矩，不能进行实时辨识。[4]-[6]采用扩展卡尔曼滤波算法进行电机参数的估计，但是算法实现过程比较复杂，难以进行工程应用。[7]-[9]采用最小二乘法求解平方和的最小值，其收敛性主要依赖于初始值的选定，容易受到工况变化的影响。并且最小二乘法进行参数辨识时需要很长的辨识时间，限制了其在实际情况下的应用。[10]采用自适应反推控制，辨识电机参数，该算法可行性较高，但比较计算复杂且只能应用于id=0 的情况下，不能适用于永磁同步电机MTPA控制。

本文提出了一个自适应的在线参数辨识算法，该算法适用于永磁同步电机的MTPA控制，并根据永磁同步电机的机械和电气数学模型，运用Lyapunov稳定性原理得到负载转矩和交直轴电感参数的自适应律，并反馈回电机控制算法中实时地更新控制参数，仿真和实验结果证明了算法的可行性。

1 永磁同步电机的数学模型

永磁同步电机在dq轴上的数学模型如下所示：

其中vd,vq为dq轴方向的定子电压，id,iq为dq轴方向的定子电流，rs为定子相电阻，Ld,Lq为dq轴方向的定子电感，ψf为永磁体产生的磁链，ωr为机械角速度，Te,TL为电磁转矩和负载转矩，Bm为电机摩擦系数，P为电机极对数，J为转动惯量(包括电机和负载)。

2 自适应在线参数辨识算法

永磁同步电机算法的控制框图如下图1所示，该算法主要可分为两部分，负载转矩TL的估算和电机交直轴电感Ld,Lq的估算。

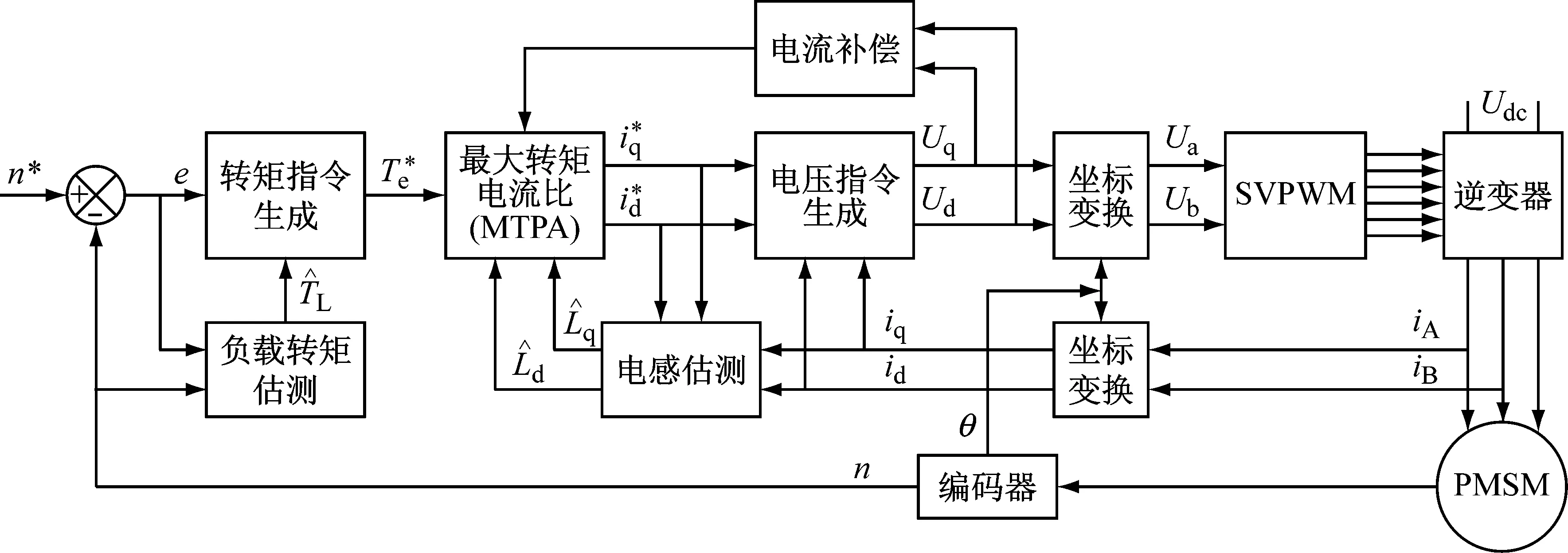
图1 永磁同步电机自适应参数辨识算法控制框图Fig.1 Block diagram of adaptive parameter estimation control algorithm for PMSM

负载转矩估算：对于永磁同步电机调速系统，其主要目标是速度跟踪，使得实际转速与需求转速保持一致，则定义速度误差为

e=ω*-ωr

(5)

定义估测负载转矩与实际转矩之间的差值为

(6)

根据公式(4)和公式(5)可得

(7)

为使速度误差趋向于零，构造如下Lyapunov函数

(8)

对公式(8)求导得

(9)

(10)

式中ks>0，自适应律为

(11)

将式(10)(11)代入式(9)可得

(12)

式(11)可以实现电机负载转矩的实时辨识，并反馈回控制系统，得到式(10)，实现永磁同步电机的速度跟踪。同时式(10)的得到的转矩指令值根据MTPA的公式法得到dq轴电流端的指令值。

交直轴电感估算：

根据电流环需求，使dq轴电流的实际值和需求值保持一致，定义电流误差为

ed=id-id

(13)

eq=iq-iq

(14)

根据所需求解的dq轴电感，定义电感估测值与实际值之间的误差为

(15)

(16)

为使电流误差与电感误差趋于零，定义Lyapunov函数为

(17)

求得公式(16)的导数为

(18)

式中，k1>0,k2>0，自适应律为

将式(19)～(22)带入式(18)中，可得

(23)

则式(11)、式(21)与式(22)可以实现电机负载和交直轴电感的参数辨识，并反馈回控制系统，实现电流的跟踪。

3 仿真

永磁同步电机参数辨识控制算法的仿真结果如下图所示，控制系统采用MTPA控制，附加弱磁模块，仿真的电机参数为如表1所示，给定转速为nref=6 000 r/min,电机负载为恒转矩TL=50 N·m。

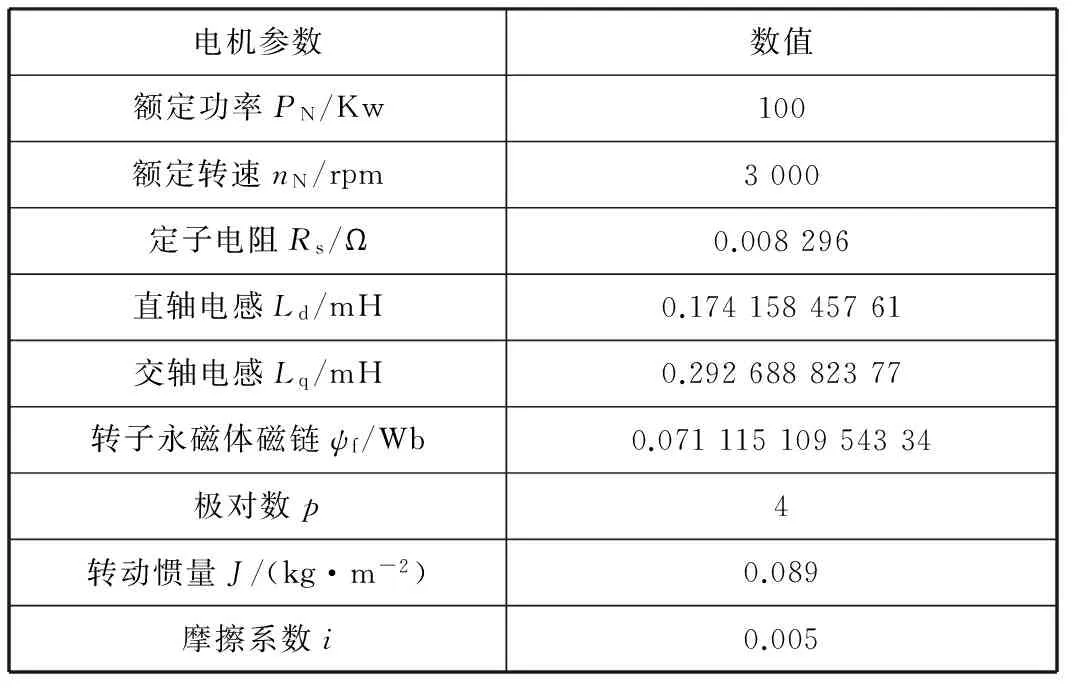
表1 永磁同步电机仿真参数

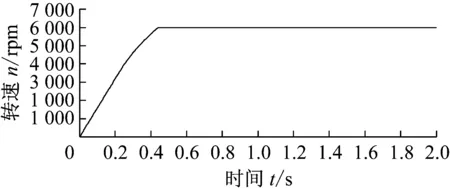
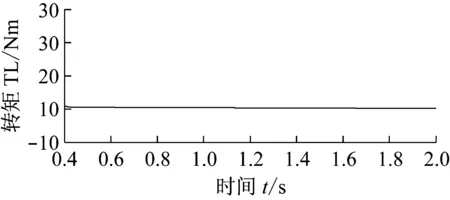
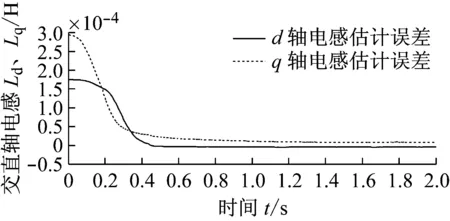
图2～4为永磁同步电机自适应参数辨识算法的仿真结果。其中图2为转速仿真图像，(a)图显示电机实际转速平稳上升至需求转速，(b)图显示稳态时电机转速误差较小。图3与图4分别为负载转矩与交直轴电感仿真图像，图中参数辨识算法所得的参数估计值较好地收敛于电机参数的真实值，参数估计值与真实值稳态误差表明永磁同步电机自适应参数辨识算法具有较高的的准确性。

(a)

(b)

(a)

(b)

4 试验结果

本试验平台由两台电驱动控制的微型电动车用永磁同步电机组成对拖系统进行试验，如图6所示，左侧为驱动电机，以Semikron系列逆变器作为驱动单元，本文所提算法在控制芯片TMS320F2810中实现；右侧为负载电机，采用默认控制器，可调节电机转矩，提供负载，电机参数如表2所示，电机实验数据由CAN通讯导出到电脑中得到，并于MATLAB中重新绘制为试验图片。

(a)

(b)

表2 永磁同步电机实验参数

图5 控制系统试验平台Fig.5 Experimental platform of motor control system

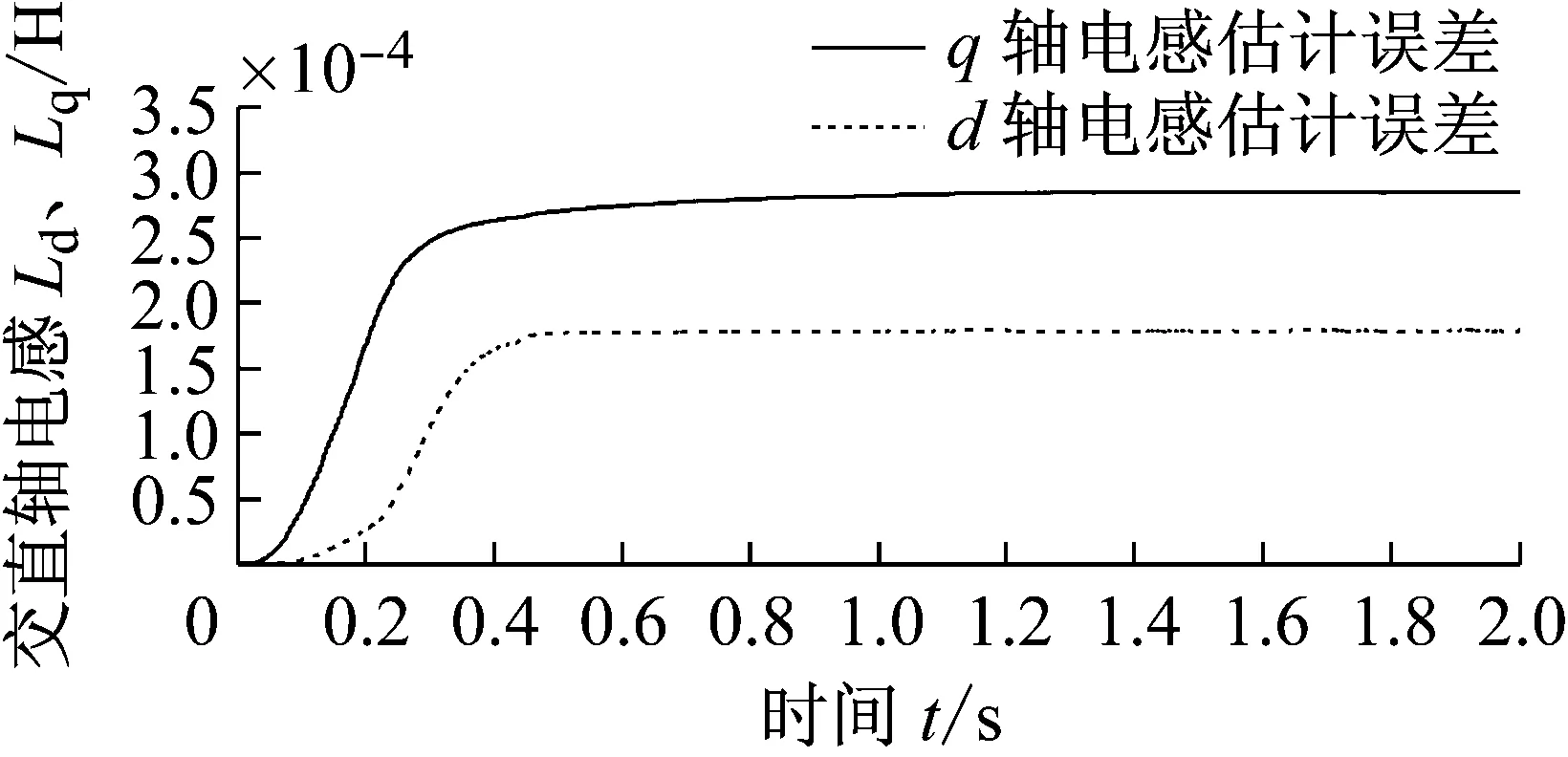
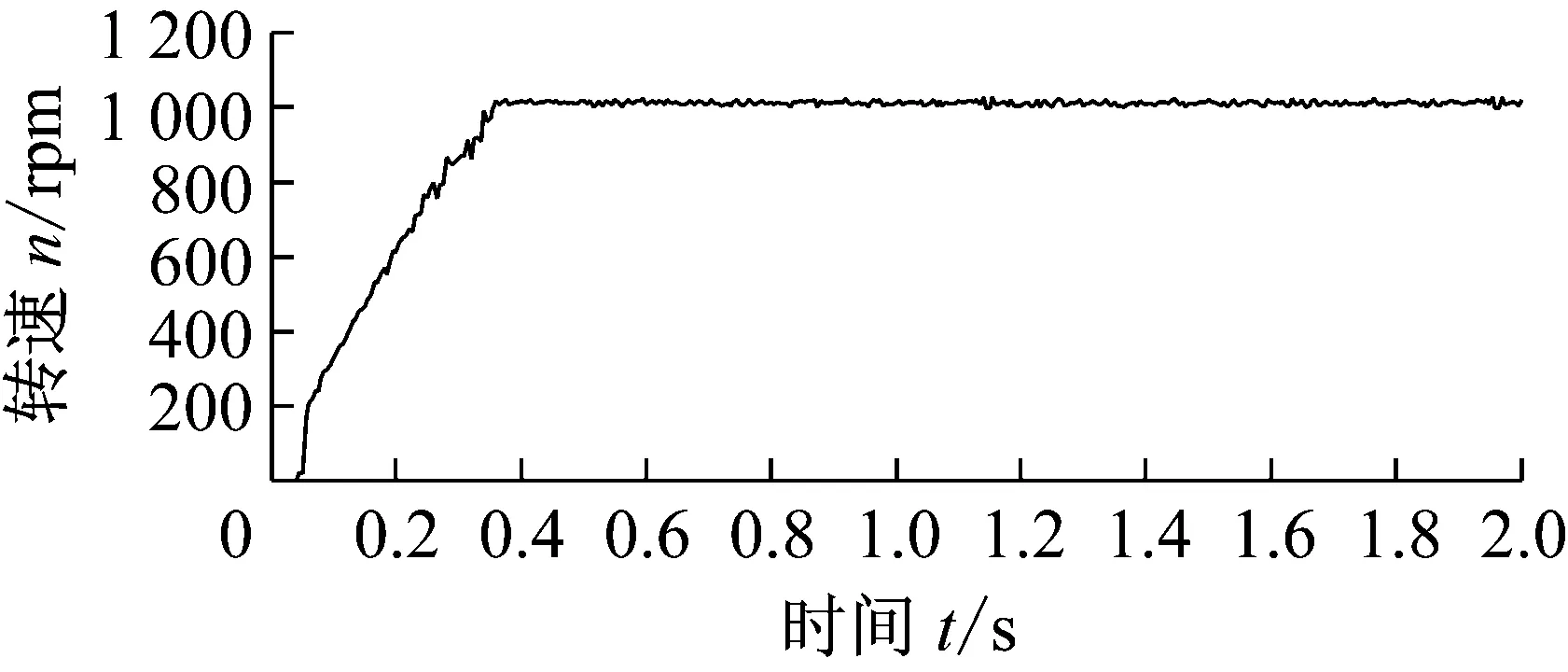
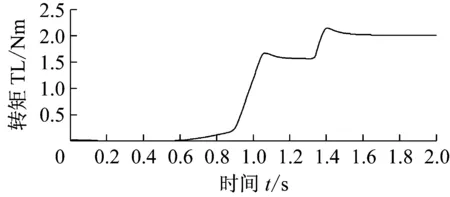
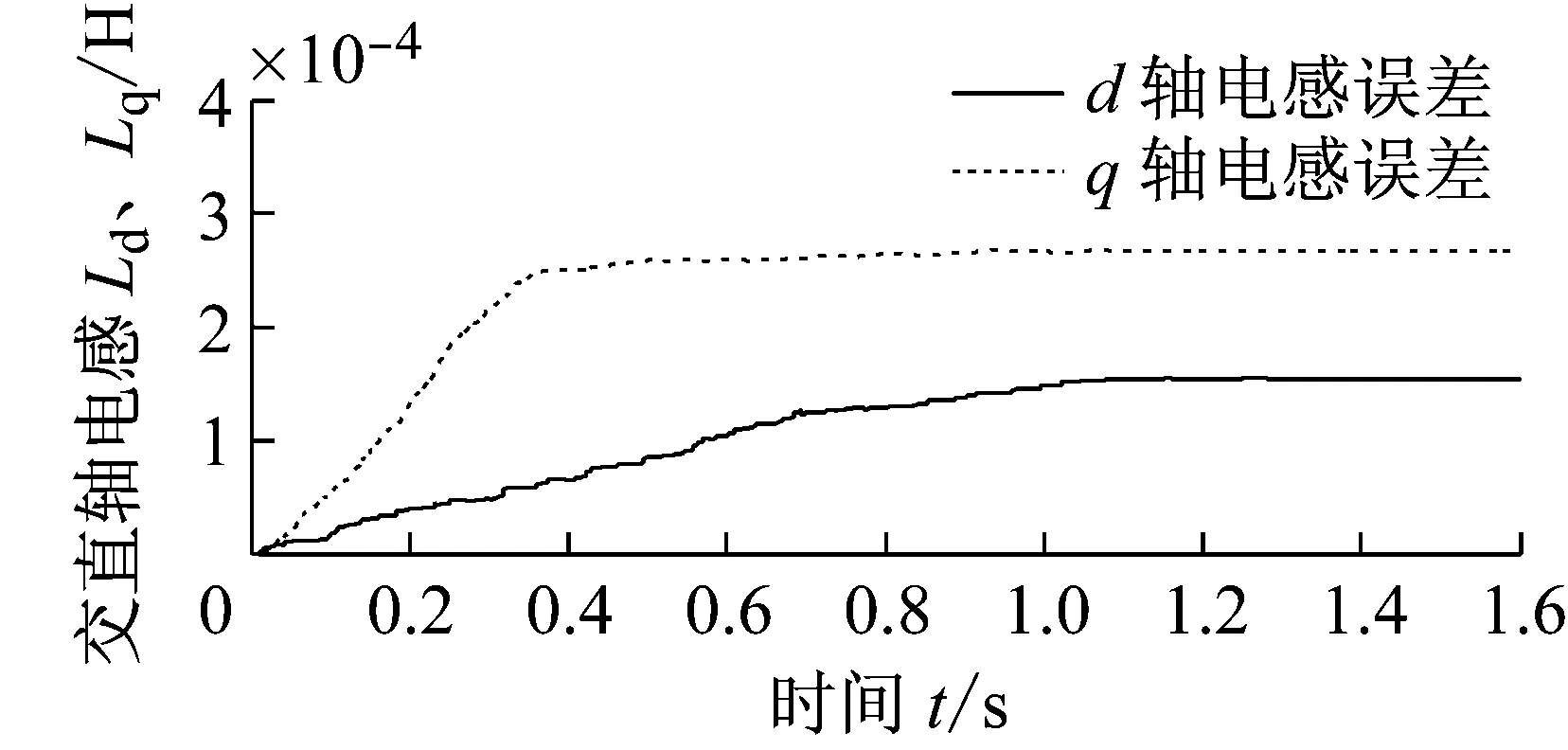
图6～9为永磁同步电机自适应参数辨识算法的试验结果，试验给定转速1 000 r/min，图6为电机转速变化过程，图7为负载转矩估算结果，实验设定负载转矩由1.5 Nm变化为2 Nm，图8为交直轴电感的估算结果，电感的实际值由[11]中的实验方法测得Ld=153 μH,Lq=264 μH。

(a)

(b)

(a)

(b)

由图6(a)(b)可见电机转速逐渐升高并稳定于需求转速，电机稳态时转速波动较小。图7(a)中永磁同步电机的自适应在线参数辨识算法的负载转矩估计的实验结果于1.2 s左右收敛于1.5 N·m，于1.6 s左右大致收敛于2.0 N·m，(b)中显示负载转矩估计值与实际值的误差满足要求。图8中电机的q轴电感参数在1.2 s之后稳定于263 mH，d轴电感估计值于1 s后稳定于152 mH，电机的参数估计值与真实值之间具有较小的误差。

5 结论

车用永磁同步电机中外部工况和工作环境变化会使电机参数变化并对电机控制性能造成影响。本文采用一种自适应的永磁同步电机在线参数辨识算法，可应用于永磁同步电机的MTPA控制，同时实时地辨识永磁同步电机的负载转矩和电感参数。仿真和实验结果表明该参数辨识算法具有很好的有效性和精确性。

(a)

(b)

[1] L. Zhao, J. Huang, H. Liu, and B. Li, “Second-order slidingmode observer with online parameter identification for sensorless induction motor drives,” IEEE Trans. Ind. Electron., vol. 61, no. 10, pp. 5280-5289, Oct. 2014.

[2] M.S. Carmeli, F. Castelli-Dezza, M. Iacchetti, and R. Perini, “Effects of mismatched parameters in MRAS sensorless doubly fed induction machine drives,” IEEE Trans. Power Electron., vol. 25, no. 11, pp. 2842-2851, May 2010.

[3] 安群涛，孙力，赵克. 一种永磁同步电机参数的自适应在线辨识方法[J]. 电工技术学报， 2008，23(6) : 31-6.

[4] H. Renaudineau, J.-P. Martin, B. Nahid-Mobarakeh, and S. Pierfederici, “DC- DC converters dynamic modeling with state observer-based parameter estimation,” IEEE Trans. Power Electron., vol. 30, no. 6, pp. 3356-3363, Jun. 2015.

[5] K. L. Shi, T. F. Shan, Y. K. Wong, and S. L. Ho, “Speed estimation of an induction motor drive using an optimized extended Kalman filter,” IEEE Trans. Ind. Electron., vol. 49, no. 1, pp. 124-133, Feb. 2002.

[6] S. Bolognani, L. Tubiana, and M. Zigliotto, “Extended Kalman filter tuning in sensorless PMSM drives,” IEEE Trans. Ind. Appl., vol. 39, no. 6, pp. 1741-1747, Nov./Dec. 2003.

[7] WANG S. Windowed least square algorithm based PMSM parameters estimation [J]. Mathematical Problems in Engineering, 2013 : 1-11.

[8] T. H. Nguyen and D.-C. Lee, “Deterioration monitoring of DC-link capacitors in AC machine drives by current injection,” IEEE Trans. Power Electron., vol. 30, no. 3, pp. 1126-1130, Mar. 2015.

[9] Y. He, Y. Wang, Y. Feng, and Z. Wang, “Parameter identification of an induction machine at standstill using the vector constructing method,” IEEE Trans. Power Electron., vol. 27, no. 2, pp. 905-915, Feb. 2012.

[10] 刘栋良, 王家军, 崔丽丽. 永磁同步电机参数自适应调速控制[J]. 电工技术学报, 2011, 26(8): 159-165.

[11] 刘金海, 陈为, 胡金高. 永磁同步电机 dq 电感参数新实验获取法[J]. 电工技术学报, 2014, 29(7): 97-103.

Adaptive On - line Parameter Identification of Vehicle Permanent Magnet Synchronous Motor

ZhengLuyangZhangXi
(ShanghaiJiaoTongUniversity,Shanghai200240)

In the course of running, the complex working condition and the bad working condition of the permanent-magnet synchronous motor (PMSM) affect the parameters of the motor and affect the motor control performance. In this paper, an adaptive parameter identification algorithm is used to identify the parameters of permanent magnet synchronous motor (PMSM) to feed back to the motor control system. Based on the mathematical model of permanent magnet synchronous motor (PMSM), the identification model of load torque and dq axis inductance is established by means of Lyapunov stability theory and then the adaptive law is deduced. Simulation and experimental results based on the MTPA algorithm show that the proposed parameter identification algorithm can achieve efficient parameter identification in a short time, and the error between the estimated value and the real value is small.

permanent magnet synchronous motor Adaptive online parameter identification MTPA

1006-8244(2017)01-010-04

U464.9

B