基于GARCH-M模型的股指期货对股市波动影响的研究
曹 栋,张 佳
(1.西安电子科技大学经济与管理学院,陕西 西安 710071;2.中国科学院数学与系统科学研究院,北京 100190)
基于GARCH-M模型的股指期货对股市波动影响的研究
曹 栋1,2,张 佳1
(1.西安电子科技大学经济与管理学院,陕西 西安 710071;2.中国科学院数学与系统科学研究院,北京 100190)
从本轮金融危机以来,伴随着沪深股市的大幅震荡,股指期货作为规避风险、价格发现、资金配置的市场工具,其稳定股市波动性的作用再次被推向了风口浪尖。在综合评价现有研究的缺陷、既有改进方法以及其应用情况后,通过在股票价格指数的生成过程中融入风险测量构建了适应我国股市的高拟合程度的GARCH-M模型,研究股指期货对股市波动的影响。本文选取2007年8月1日到2015年4月23日沪深300股票指数的日度数据,分析了我国股市在受到较大外部冲击后,股指期货的稳定作用以及股票市场的正反馈效应等。实证结果表明:我国股票市场波动表现出正反馈效应,股指期货推出前后表现出不同程度的波动性,并且呈现出明显的“波动集群性”;沪深300股指期货推出后股指的波动平均减小了4.45×10-6个单位,已经初步发挥了股票市场的稳定器功能,一定程度上缓解了股市波动,但是其作用有限,功能还未能完全发挥;市场波动受旧信息的影响远大于新信息产生的影响,表明我国股市波动主要来源于前者,同时条件方差所受的冲击是持久的,即冲击对未来的股票指数走势都有重要作用。
沪深300股指期货;股市波动;GARCH-M模型
1 引言
股指期货是期货交易的一种,以股票指数为标的,按照约定的交易日期和交割数量,通过现金结算差价的形式,进行标的的指数买卖。价值线综合指数期货合约是全球最早股指期货,于1982年2月24日在美国堪萨斯期货交易所推出。由于其在规避价格风险、价格发现、提高资金配置效率等方面的作用,受到各界广泛关注。时至今日,全球已经陆续推出上百支股指期货。股指期货更是学界研究热点,学者们对各国股指期货进行了深入研究。Cervello-Roy,Guijiarro和Michniuk[1]运用改进的flag pattern方法,通过分析91307个日度DJIA指数数据,验证了IF-THEN规则在美国股指期货市场交易的有效性。Kittiakarasakun,Tse和Wang[2]基于2002年到2004年Nasdaq-100股指期货数据,研究了知情交易者和不知情交易者在不对称波动的影响,分析结果表明不知情交易者的交易行为,尤其是小额交易行为,更显著地导致了市场的不对称波动。Christain和Claudia[3]结合Vine copula和GARCH模型,研究了欧洲最大的股指期货Euro Stoxx 50的金融风险控制问题。Frijins和Tse[4]通过分析2001年到2011年的FTSE 100指数,研究了英国股指期货市场交易诱导和报价诱导情况,知情交易者可以在80%的程度上解释有效价格的创新。但是在本轮金融危机和欧洲债务危机时,由于噪声交易者数量突增,知情交易者比重急剧下降。Laurent,Carole, Béatrice(2014)研究了法国股指期货市场,通过研究在第一支以CAC40为标的的交易所买卖基金(ETF)上市前后各五个月的高频数据,分析了其对现货和期货市场上价格的直接和间接作用,研究表明ETF上市后,市场表现出显著的无套利行为。Wagner和Matanovic[6]基于GARCH模型,研究了1970年到2009年德国的DAX指数,结果表明虽然股指期货对现货市场波动作用存在时滞,但是其对股票市场稳定和波动缓解作用是显著的。Lee[7]利用CBP-GARCH模型,研究了1998年1月5日到2012年2月29日的Nikkei 225和VXJ指数,结果表明日本期货市场的收益对投资者情绪有显著影响,但是这种关系在本轮金融危机期间变得不显著。Fung等[8]研究了2006年1月到2011年12月香港股指期货和现货市场,结果表明选取不同频率的Hang Seng数据,获得股指期货和现货市场的套利效应具有显著差异。
我国股市虽然创建历史不长,但是在积聚资本、风险管理等方面取得了良好的成效,已经成为宏观经济晴雨表。由于宏观经济运行的不确定性、信息不对称性、市场参与者的非理性行为以及制度因素等诸多因素的共同影响,使得市场收益偏离预期,从而造成股市的波动性。譬如,股票市场普遍存在正反馈交易行为,交易者作出高买低卖的交易决策,引起股市过度波动;加之我国股市起步较晚,投资者结构不完善,相关金融衍生品数量较少,监管以及法律制度等影响,股市异常波动现象时有发生。2007年爆发的经济危机以来,全球金融体系持续调整,引发了各国股市的巨幅波动,面对国内外错综复杂的经济形势,我国股市波动性风险加大。侯利强等[9]通过引入模糊逻辑系统以及利用已实现的波动率替代隐含波动率的方法进行上证综指的波动预测。我国股市波动还受到外部风险影响:唐振鹏等[10]利用小波方法,发现中国股市与亚太十个主要股市在时间和时间尺度的联动存在变化,尤其是在金融危机期间联动性增强。
我国大陆第一支股指期货沪深300股指期货合约以沪深300指数为标的,于2010年4月16日正式上市交易。虽然上市时间较短,但对沪深300股指期货的研究取得了丰富的成果。前期研究主要集中在股指期货的运行特征,与现货市场的相互影响以及与国际股指期货市场的联动关系等方面。在股指期货运行特征方面:Chen Zhijuan等[11]通过分析2010年4月16日到 2012年12月31日沪深300股指期货的逐笔交易数据,研究了该市场的波动情况,结果表明在午间时段该市场的交易额和波动有很明显的下降,在下午时段该市场的交易额和波动表现出显著的倒U型,在上午时段交易者数量呈倒L形。He Xiaoli等[12]研究了2006年4月5日到2014年5月9日沪深300指数,通过运用多重趋势波动模型(MF-DFA)研究了股指期货市场的复杂分形性态。对收益率序列的分析表明在沪深300股指期货上市后存在分形,市场的有效性显著提高,同时复杂性减弱。与现货市场相互影响方面:刘睿智和周勇[13]从微观订单流动性角度出发,通过构建期现货订单流动性传染互动模型,使用股指期货和沪深300指数现货的高频数据,发现股指期货和现货之间的“遛狗效应”。Yang Jian等[14]研究了从沪深300股指期货上市以来的日度数据,即2010年4月16日到2010年7月30日的数据,发现在股指期货推出之初,中国股市出现很大跌幅,股指期货在价格发现方面作用不显著,现货市场在价格发现方面仍然具有主导作用。Zhou Pu[15]通过非线性的Granger因果检验研究了中国股指期货市场,发现从期货市场到现货市场存在显著的正向溢出效用,从现货市场到期货市场存在显著的负向溢出效用。另外,Biao Guo等[16]分析了2011年5月到11月中国股市沪深300指数和新加坡A50指数的1分钟和5分钟高频数据,利用Granger因果检验以及GARCH模型,发现前者在价格发现以及波动控制上表现都优于后者。
沪深300股指期货的推出加快了市场中信息的传递速度,提升了价格发现能力,提升市场参与程度,可以显著减弱股市的波动。简志宏等[17]研究了沪深300股指期货,发现其隔夜收益序列具有右偏、无长期记忆性和尖峰厚尾等典型特征,对CAViaR模型的实证分析表明股指期货的波动受到隔夜风险的影响。周仁才[18]和代军,朱新玲[19]则分别从股指期货在套期保值、风险对冲等方面稳定股市波动的作用进行分析。综上可知股指期货对股市波动的影响尚无统一定论:现有研究普遍关注股指期货推出后其具体功能,或研究不同阶段股指期货的稳定性功能,却忽略了在受到较大外部冲击时,针对股市期货对现货市场稳定作用进行深入的研究;另外,现有研究主要是针对股指期货的特有性质进行分析,本研究综合考量样本区间内各因素的综合影响,进而全面测度股指期货的稳定性作用。
基于此,鉴于股指期货对我国股票市场的深刻影响,测度金融危机后股指期货推出至今对股票市场波动的影响,有助于理清股指期货与现货市场的关系,发挥股指期货风险控制的作用,对促进股票市场良性发展,具有重要的现实和理论意义。而选取较长的时间跨度的数据结合中国证券市场的发展情况分析股指期货对股市的影响,将克服以往研究时间跨度较短的缺陷。
本文所做的主要工作在于,研究股指期货推出对股市波动的综合影响,以金融危机为代表的外部冲击下,较长时间段内股市的波动集聚性,通过偏度、峰度值等统计指标分析进行测度,研究了股市的波动集群性,在考虑股市高风险高收益特征的基础上,构建了GARCH-M波动分析模型,对比分析了引入股指期货之后我国股市的波动变化情况,研究了股指期货对股市波动的稳定功能,以及市场旧息和新息的作用。在研究范式设计上,本文考量我国股市的特殊情况,通过结合统计分析并构建带有高风险高收益特征的GARCH-M模型,综合测度股指期货的影响。该GARCH-M模型通过将收益率的条件方差作为滞后条件方差项和前期误差平方项的线性函数,同时引入表征股指期货推出的虚拟变量,捕捉收益序列波动在股指期货推出前后的聚集趋势及其结构性变化,并检验新息和旧息与波动性的关系。
本文选取2007年8月1日至2015年4月23日沪深300价格指数的日度收盘数据,分析股市受到强烈外部冲击后,股指期货对股票市场波动的影响。文章结构如下:第一部分是引言;第二部分是模型介绍;第三部分是数据处理;第四部分通过在股票价格指数的生成过程中融入风险测量,构建GARCH-M测度股指期货对股市波动的影响,同时对实证结果进行了解释与分析,是本文的核心内容;第五部分是结论。
2 GARCH-M模型
GARCH模型最早由Bollerslev[20]提出,可以用来描述经济问题中常常出现的依赖前期变化量的条件异方差现象。由于其可以较为简单且准确的刻画出市场的波动特性,因此获得广泛应用[21],尤其是在金融领域,采用日度数据或周数据的股票市场波动性方面应用更是如此[22]。标准GARCH(p, q)模型的均值方程和条件方差方程形式定义如下:
yt=xt′γ+utt=1,2,…,T
(1)
(2)
其中p是ARCH项的阶数,q是GARCH项的阶数,p>0,βi≥0,1≤i≤p。且α(L)和β(L)是滞后算子多项式。αi是滞后期残差平方项的系数,它表示了新信息对市场波动性的影响,βi是滞后期条件异方差项的系数,它表示了旧信息对市场波动性的影响。

(3)
(4)

3 数据处理
3.1 数据选取
沪深300股指期货于2010年4月16日正式上市交易,交易的标的物是沪深300股票指数。为了更准确的刻画出沪深300股指期货的推出前后现货市场的波动特性,尤其是在金融危机爆发后沪深300股指期货对现货市场的影响,本文以金融危机开始显现的2007年8月1日为样本数据的起始日期,以2015年4月23日为样本数据的终止日期,选取沪深300股票指数的日收盘价共2017个样本数据。所有数据均来自于新浪财经网。同时对数据进行了节假日处理,即非周末的休市日期,按照最近一个交易日的数据进行补齐,最终处理指数是频率为一周五天的日数据。本文选取沪深300股票指数的收盘指数的日数据序列{spt}检验股票价格指数的波动。为了减少舍入误差,在估计时,对{spt}进行自然对数处理,即将序列{ln(spt)}作为因变量进行估计。
3.2 统计描述
沪深300指数收盘价趋势见图1和图2,从中可以看出,金融危机爆发后股市出现较大波动,股指期货上市后股市波动幅度较小。从表1可以看出,沪深300指数spt及其对数序列ln(spt)的偏度值S均大于0,说明序列分布有长的右拖尾,即右偏;峰度值K都高于正态分布的峰度值3,呈现出高峰的形态。因此,都具有典型金融数据所表现出的高峰厚尾、有偏的统计特性,同时,沪深300股票指数日度价格序列及其对数序列表现出的高峰厚尾特性反映了波动的正相关性,说明股票市场具有正反馈效应。
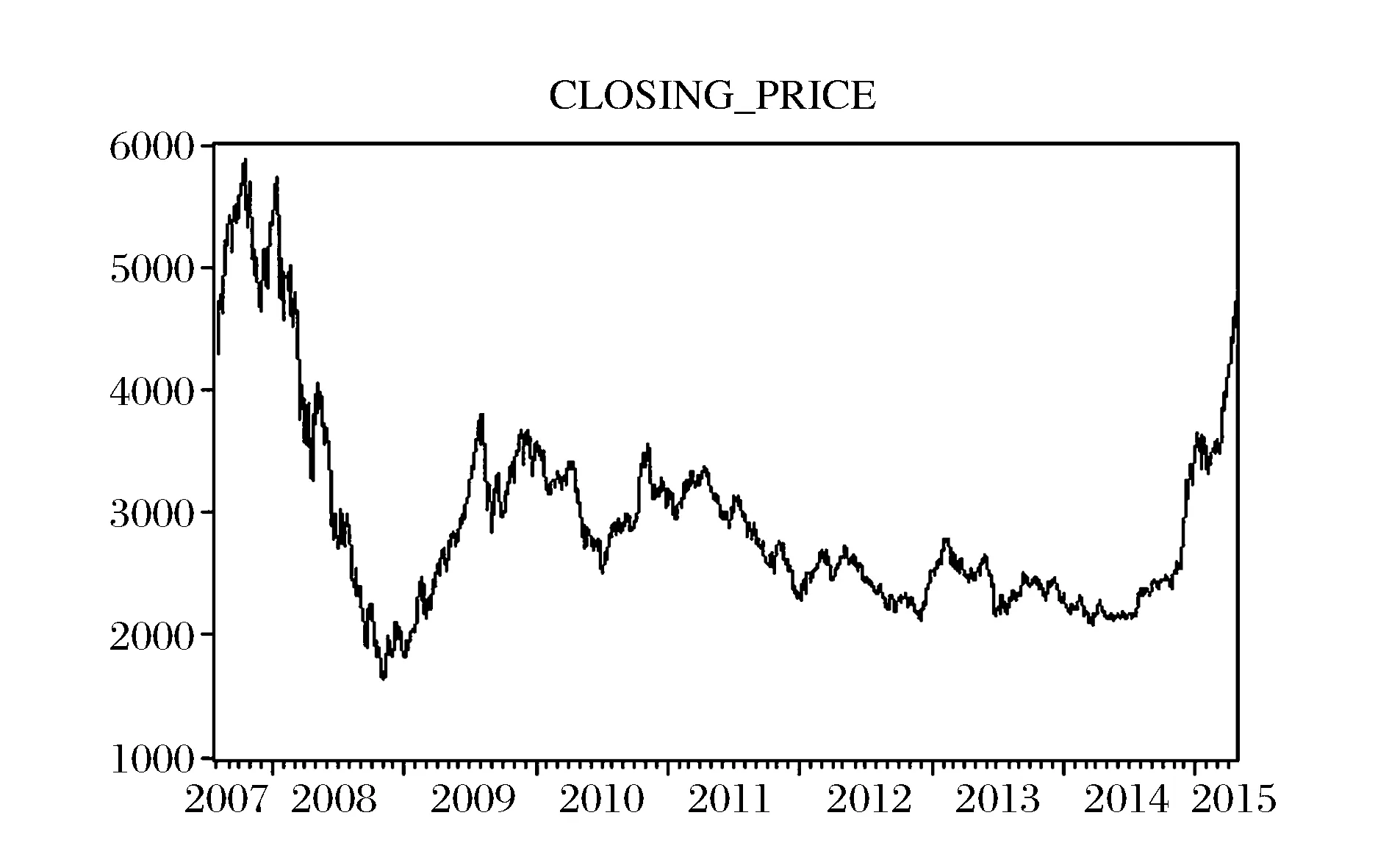
图1 沪深300指数收盘价趋势图
当市场出现暴涨暴跌时,非理想的投资者容易产生羊群效应,造成追涨杀跌的效果,使得市场一旦出现波动变化,则波动变化的趋势将持续下去,直到另一个变化的出现。
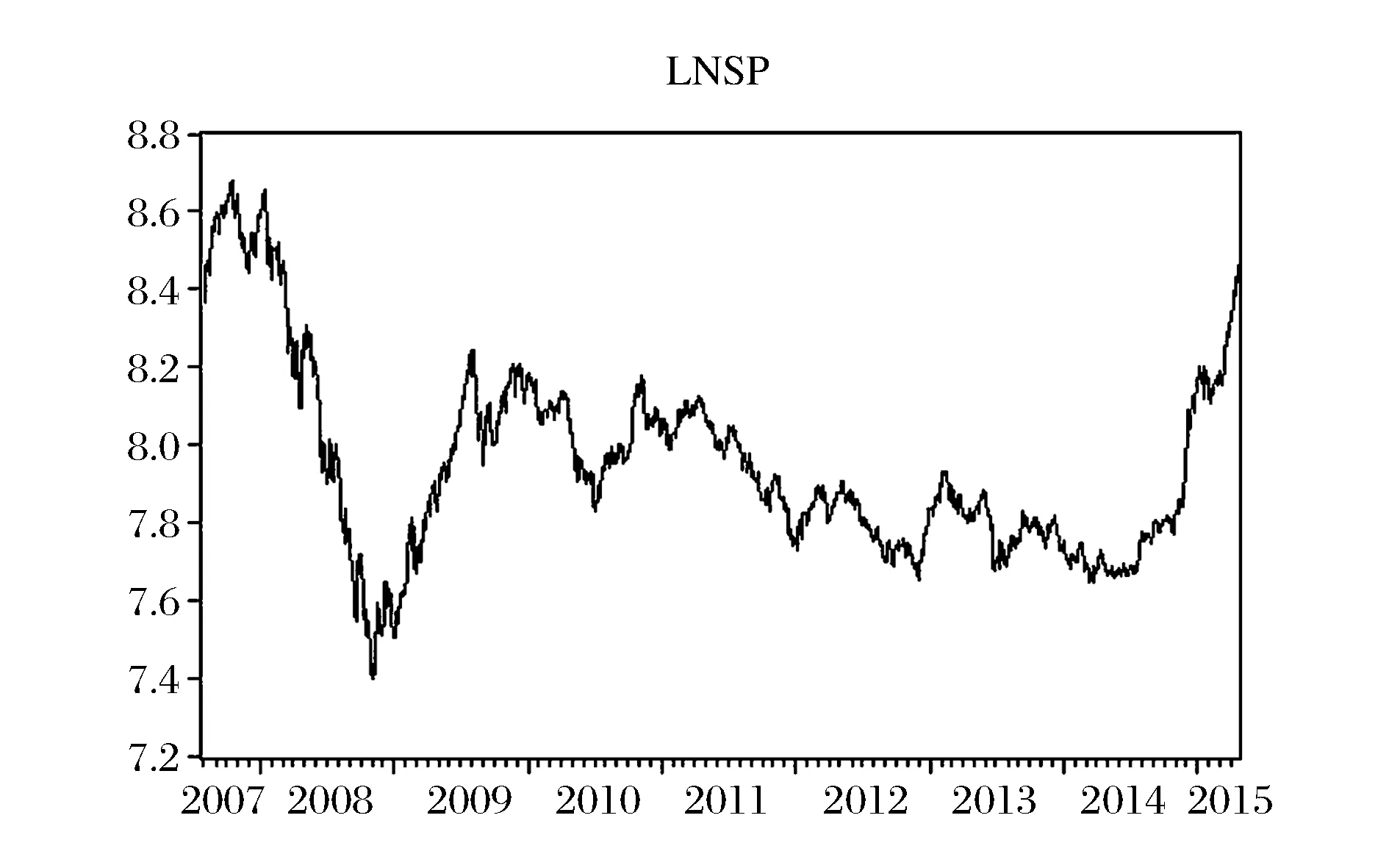
图2 {ln(spt)}走势图
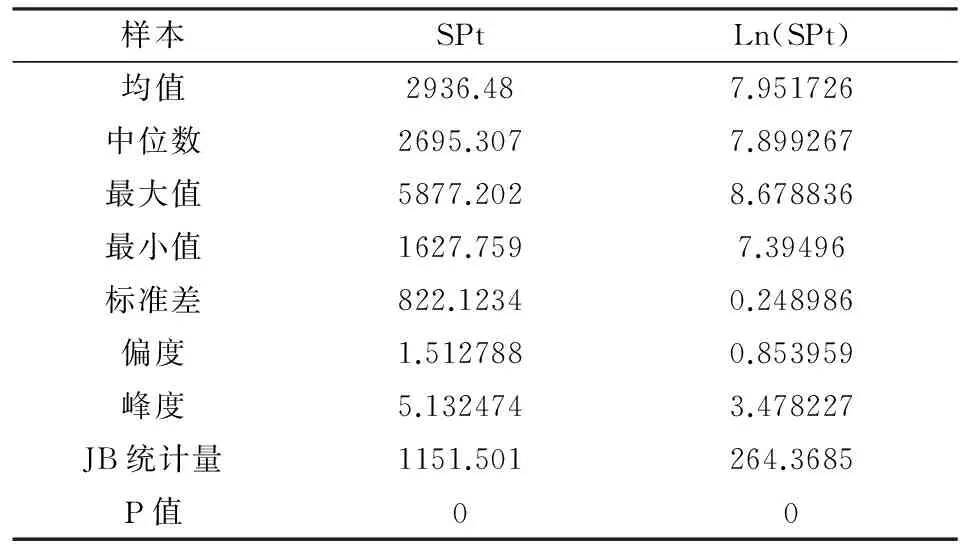
表1 沪深300指数spt及ln(spt)统计性描述
4 实证分析
由于股票价格指数序列经常用一种特殊的单位根过程:带漂移的随机游走(random walk)模型描述,所以本文对如下形式的随机模型进行估计:
ln(spt)=μ+ρln(spt-1)+ut
(5)
利用最小二乘估计结果如下:
t=(1.362752) (631.1041)
(6)
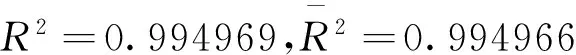
对数似然值=5278.200,AIC=-5.234325,SC=-5.228761
该方程的统计量很显著,拟合的程度也很好。另外,该回归方程对应的残差图(见图3),可以注意到波动的“成群”现象:波动在一些较长的时间内非常小(例如2012年),在其他一些较长的时间内非常大(例如2008年、2009年),这说明误差项可能具有条件异方差性。接下来用ARCHLM检验和残差平方的自相关(AC)和偏自相关系数(PAC)来检验条件异方差性。
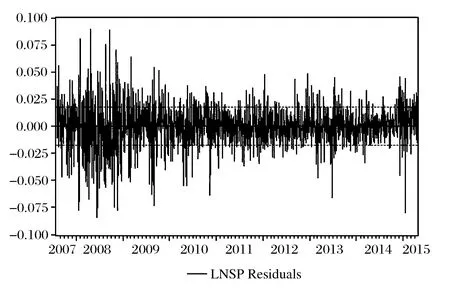
图3 沪深300价格指数OLS回归方程的残差
4.1 ARCH效应检验
对线性回归方程进行条件异方差的ARCH LM检验,取滞后阶数1到6时的ARCH LM检验结果见表2。
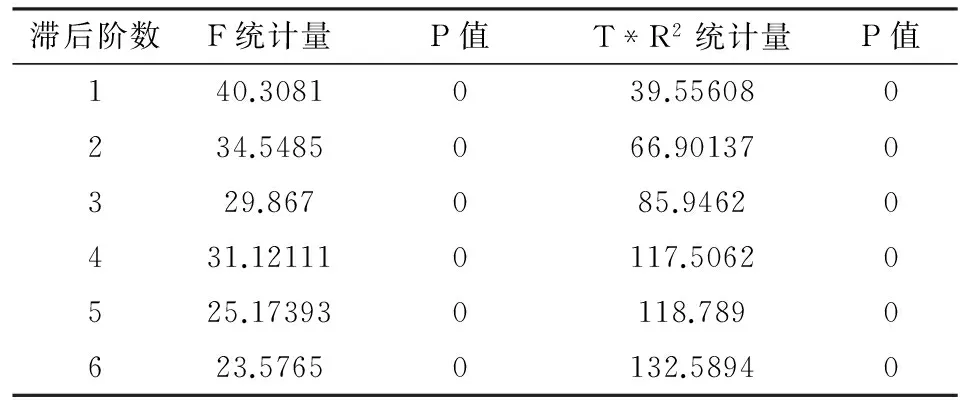
表2 ln(spt)序列的ARCH LM检验结果
此处的1到6阶滞后项对应的P值都为0,拒绝原假设,说明线性回归方程的残差序列存在ARCH效应。同时,使用残差平方的自相关(AC)和偏自相关系数(PAC),结果如下:
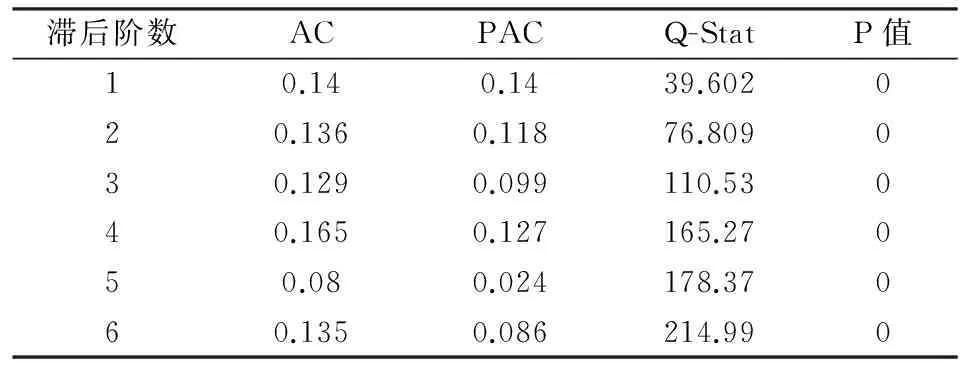
表3 ln(spt)序列残差平方的自相关和偏自相关系数
由于1到6阶滞后项的自相关(AC)和偏自相关系数(PAC)值显著不为0,且Q统计量非常显著,所以可以得出结论:线性回归模型的残差序列存在ARCH效应。
4.2 基于GARCH-M模型的波动性分析
在金融市场中,具有较大的可观测到风险的资产,一般来说具有较高的预期收益。GARCH-M模型引入之初就是用来揭示风险和收益之间这种关系,之后便广泛应用于资产的预期收益与预期风险密切相关的金融领域。本文构建如下GARCH-M模型估计股票价格指数,其变化依赖于一个常数项,以及股票价格指数的条件方差的对数:
(7)
式中,残差ut服从条件标准正态分布。为了研究股指期货的推出对股票市场波动性的影响,本文在条件异方差方程中引入虚拟变量D1,在沪深300股指期货推出前该值为0,在沪深300股指期货推出后该值为1。因此GARCH-M模型的均值方程为(7),条件方差方程为:
(8)
可以根据虚拟变量前的参数η的统计性质是否显著来判断沪深300股指期货的推出是否对现货市场中沪深300股票指数的波动性产生了影响。
对上述均值方程和条件方差方程进行检验,估计结果为:
ln(spt)=0.036234+0.996755ln(spt-1)
z=(2.157226) (589.1332)+
(9)
z=(3.686361) (7.488128)+
(117.3676) (-2.906958)
(10)
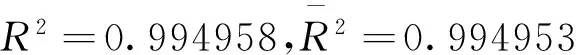
对数似然值=5496.942,AIC=-5.446371,
SC=-5.439223
均值方程的估计结果显示其变量都通过了显著性检验,拟合程度也很高。同时条件方差方程中的ARCH项和GARCH项的系数也都是统计显著的,并且对数似然函数有所增加,对应的AIC和SC值都变小了,这说明GARCH-M模型能够更好的拟合数据。再对均值方程(9)进行条件异方差的ARCHLM的检验,得到残差序列在滞后1阶到6阶时的检验结果。
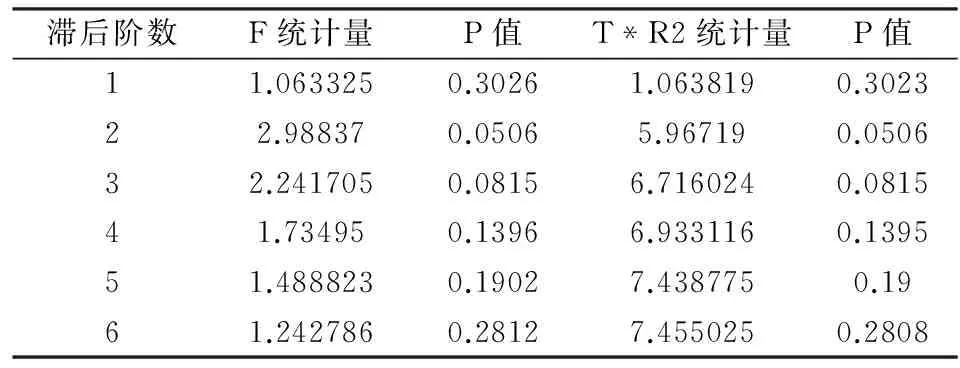
表4 GARCH-M模型残差序列的ARCH LM检验
此时的相伴概率较大,显著不为0,不拒绝原假设,认为该残差序列不存在ARCH效应,说明GARCH-M模型消除了残差序列的条件异方差性。GARCH-M模型对应的残差平方相关图的检验结果见表5。自相关系数和偏相关系数近似为0,Q统计量也变得不显著。这个结果也说明残差序列不再存在ARCH效用。
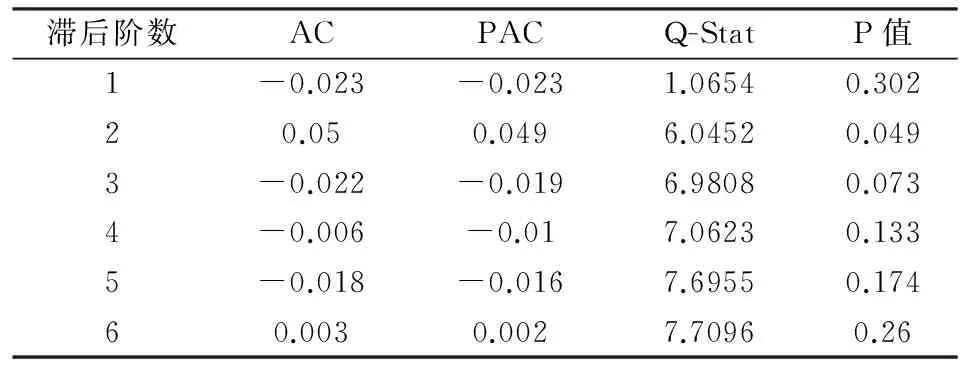
表5 GARCH-M模型残差平方的自相关和偏自相关系数
5 结语
本文选取2007年8月1日至2015年4月23日沪深300股票收盘价格日度数据及其对数,构建GARCH-M模型,研究了股票市场在受到巨大外部冲击,即金融危机后股指期货的推出对其市场波动性的影响。获得如下基本结论:(1)、沪深300股票指数日收盘价格序列及对数序列具有典型金融数据所表现出的高峰厚尾、有偏的统计特性,反映了波动的正相关性,说明股票市场具有正反馈效应。(2)样本区间内,沪深300股票指数日收盘价格序列及对数序列在不同的时期表现出不同的波动性,并且呈现出明显的“波动集群性”:在金融危机后,股指期货未推出前的2008年和2009年等年份一些较长的时间内波动非常大,在股指期货推出后的2012年等一些较长的时间内波动非常小。
综上所述,在我国经济受到巨大外部冲击且股市产生较大波动的背景下,沪深300股指期货的推出改善了股票市场的波动性,发挥了股指期货稳定市场、价格发现以及减小和规避资本市场风险的功能,有利于资本市场尤其是股票市场的长远发展。另一方面,由于我国股市历史较短,股指期货上市时间较短、进入门槛较高等原因,导致股指期货对缓解股市波动作用有限,随着股指期货市场发展的日趋成熟,投资者的投资理念和证券市场相关法律法规的不断完善,股指期货将充分发挥其规避风险,减小股市波动的市场功能。同时,应以此为契机合理发展我国的金融衍生品市场,来提升市场在资源配置和风险管理中的地位,最终提升我国在世界金融市场的竞争力。
[1]Cervello-RoyoR,GuijarroF,MichniukK.Stockmarkettradingrulebasedonpatternrecognitionandtechnicalanalysis:ForecastingtheDJIAindexwithintradaydata[J].ExpertSystemswithApplications, 2015, 42(14): 5963-5975.
[2]KittiakarasakunJ,TseY,WangGHK.TheimpactoftradesbytradersonasymmetricvolatilityforNasdaq-100indexfutures[J].ManagerialFinance, 2012, 38(8): 752-767.
[3]ChristainBE,ClaudiaC.Riskmanagementwithhigh-dimensionalvinecopulas:AnanalysisoftheEuroStoxx50 [J].StatisticsandRiskModeling, 2013, 30(4): 307-342.
[4]FrijinsB,TseY.TheinformativenessoftradesandquotesintheFTSE100indexfuturesmarket[J].Journaloffuturesmarkets, 2015, 35(2): 105-126.
[5]DevilleL,GresseC,deSéveracB.DirectandindirecteffectsofindexETFsonspot-futurespricingandliquidity:EvidencefromtheCAC40index[J].EuropeanFinancialManagement, 2014, 20(2): 352-373.
[6]WagnerH,MatanovicE.Volatilityimpactofstockindexfuturestrading-arevisedanalysis[J].JournalofAppliedFinanceandBanking, 2012, 2(5): 113-126.
[7]LeeYH.WhatjumpeffectsareimplicitinNikkei225returnsandthechangesinthevolatilityindexJapan? [J].InvestmentAnalystsJournal, 2014, 43(80): 71-78.
[8]FungJWK,LauF,TseY.Theimpactofsamplingfrequencyonintradaycorrelationandlead-lagrelationshipsbetweenindexfuturesandindividualstocks[J].JournalofFuturesMarkets, 2015, 35(10): 1-14.
[9] 侯利强,杨善林,王晓佳,等.上证综指的股指波动-基于模糊FEGARCH模型以及不同分布假设的预测研究[J]. 中国管理科学,2015,23(6): 32-40.
[10] 唐振鹏,周熙雯,黄友珀,等.基于小波方法的中国股市与亚太股市联动性实证研究[J].中国管理科学,2015,23(s):398-404.
[11]ChenZhijuan,LinHai,MaChangfeng.OnthereverseU-shapedintradaypatternofvolumeandvolatility:EvidencefromCSI300indexfuturesmarket[J/OL].AvailableatSSRN:http://ssrn.com/abstract=2386457orhttp://dx.doi.org/10.2139/ssrn.2386457.
[12]HeXiaoli,WangHongwu,DuZiping.ThecomplexityandfractalstructuresofCSI300beforeandaftertheintroductionofCSI300IF[J].PhysicaA:StatisticalMechanicsandItsApplications, 2014, 414: 76-85.
[13] 刘睿智, 周勇.期现货市场订单流动性层面的“遛狗效应”——基于交易量刻度的高频交易数据研究[J]. 中国管理科学, 2016,24(4): 19-26.
[14]YangJian,YangZihui,ZhouYinggang.Intradaypricediscoveryandvolatilitytransmissioninstockindexandstockindexfuturesmarkets:EvidencefromChina[J].Journaloffuturesmarkets, 2012, 32(2): 99-121.
[15]ZhouPu,LuFengbin,WangShouyang.TestinglinearandnonlineargrangercausalityinCSI300futuresandspotmarketsbasedonnewconceptsofnonlinearpositive/negativespillover[J].JournalofSystemsScienceandComplexity, 2014, 27(4): 729-742.
[16]GuoBiao,HanQian,LiuMaonan,etal.Ataleoftwoindexfutures:TheintradaypricediscoveryandvolatilitytransmissionprocessesbetweentheChinafinancialfuturesexchangeandtheSingaporeexchange[J].EmergingMarketsFinanceandTrade, 2013, 49(S4): 197-212.
[17] 简志宏,曾裕峰,刘曦腾.基于CAViaR型的沪深300股指期货隔夜风险研究[J].中国管理科学.2016, 24(9):1-10.
[18] 周仁才. 基于风险分解的股指期货套期保值策略研究[J].中国管理科学,2013, 21(2): 17-23.
[19] 代军,朱新玲.沪深300股指期货对冲效率研究[J].中国管理科学.2014, 22(4): 1-8.
[20]BollerslevT.Generalizedautoregressiveconditionalheteroscedasticity[J].JournalofEconometrics, 1986, 31(3):307-327.
[21] 罗万纯,刘锐. 中国粮食价格波动分析:基于ARCH类模型[J]. 中国农村经济, 2010, (4): 30-47.
[22] 周舟,董坤,汪寿阳. 基于欧洲主权债务危机背景下的金融传染分析[J]. 管理评论, 2012, 24(2): 3-11.
[23]RobertE,LilienDM,RobinsRP.Estimatingtimevaryingriskpremiainthetermstructure:TheARCH-Mmodel[J].Econometrica, 1987, 55(2): 391-406.
TheImpactofIndexFutureonStockMarketVolatilityBasedontheGARCH-MModel
CAO Dong1,2,ZHANG Jia1
(1. School of Economics and Management, Xidian University, Xi′an 710126, China;2. Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing 100190, China)
Since the financial crisis from 2007, the Chinese stock market has experienced large volatilities. CSI300 future has received a great deal of attention in recent years for its market stable function, even though it′s made to be as a hedge against the risk, price discovery, and market capital allocation tool. After analyzing shortages of existing researches, methods and their applications, the integration of risk measurement process is introduced into the GARCH-M model to measure the volatility of stock market and study the effect of stock index futures on stock market fluctuations. By using the daily data of CSI 300 from August 1st, 2007 to April 23rd, 2015, a highly fitting GARCH-M model is built. The empirical study shows the impact of CSI 300 index future on the stock market volatility after the large external shock. First, there is a positive feedback in the stock market, with different levels of volatility before and after the introduction of stock future and exhibits significant "volatility clustering". Second, the CSI 300 index future has reduced the volatility index of the average 4.45×10-6units, played a function as a controller, and eased the stock market volatility to some extent. However, its impact is limited and not fully realized. Finally, the market volatility in China is mainly affected by the old information far more than the new information, while its impact on the conditional variance is durable and has an more important role for the future impact of stock index movements.
CSI300 futures; stock market volatility; GARCH-M model
1003-207(2017)01-0027-08
10.16381/j.cnki.issn1003-207x.2017.01.004
2015-05-18;
2016-05-23
国家自然科学基金资助项目(71303181);国家留学基金委公派高级研究学者及访问学者项目(201406965014);教育部人文社会科学研究项目(11YJC790004);博士后面上基金项目(2014M550864);中央高校基金科研业务费专项资金资助项目(7214566601,7215566603);湖南省现代服务业研究基地基金项目(16jdmszd01)
曹栋(1982-),女(汉族),湖南益阳人,西安电子科技大学经济与管理学院,副教授,研究方向:宏观经济分析,金融发展、环境经济学,E-mail:ivycaodong@163.com.
F830
A

