偏移量构造细分格式的最高求和规则
亓万锋, 王金玲
(辽宁师范大学 数学学院, 辽宁 大连 116029)
偏移量构造细分格式的最高求和规则
亓万锋, 王金玲
(辽宁师范大学 数学学院, 辽宁 大连 116029)
细分格式是一种重要的曲线曲面造型方法,因优点众多而得到广泛应用. 细分格式的一种重要性质是求和规则,它与细分的收敛性、光滑性、多项式生成性和细分的逼近阶等众多性质紧密相关. 添加偏移量是构造细分格式的一种重要方法,但以往的研究并没有探讨添加偏移量构造细分能够达到的最高阶求和规则.针对对称的细分生成函数,当限定添加的偏移量的支集包含原生成函数支集时,添加偏移量方式构造的细分格式可达到最高阶求和规则.当采用二阶差商的线性组合作偏移量构造细分格式时,若原生成函数满足二阶求和规则,则添加二阶差商的线性组合也可达到最高阶求和规则.
细分格式;求和规则;偏移量;二阶差商
细分方法是将给定的控制多边形或网格,利用迭代格式加细,生成光滑曲线或曲面的造型方法. 迭代格式简单,并适用于各种拓扑类型的网格,因而在CAGD等众多领域中应用广泛.
细分方法可以追溯到Chaikin的多边形“砍角”算法[1],生成的极限曲线是二次B样条曲线.此后众多学者提出了各种曲线曲面细分格式. 近年来,采用局部操作,建立构造细分格式的统一框架成为一个热点[2-10].从细分生成函数的角度来看,典型的局部操作可分为乘以一个Laurent多项式和加上一个Laurent多项两种形式. 乘以Laurent多项式对应了局部的平均操作[6-7],加上一个Laurent多项式对应了在顶点处加上某些偏移量[8-10].添加偏移量多用来从逼近型细分构造插值型细分[8-10].檀结庆等人[11]利用添加偏移量的方式,从Hassan[12]三重插值型细分构造逼近型细分.这些结果丰富了细分的理论,提供了许多新的认识.

笔者系统研究采用偏移量构造细分格式能够达到的最高阶求和规则. 首先,指出m重细分采用偏移量方法能达到的最高阶求和规则.对二重逼近型细分,具有最高阶求和规则的是B样条细分,插值型细分中具有最高阶求和规则的是Dubuc-Deslauriers插值型细分. 其次,分析了对任意m重细分,在一定条件下,采用顶点的二阶差商作偏移量,也能够达到最高阶求和规则.
1 预备知识

其中,序列a={ai}i∈∈l0(),称为该细分格式的掩模,l0()代表上的所有有限支撑的序列,正整数m称为重数. 对应于上述迭代格式的细分格式记为S,并将Laurent多项式({0} )称为对应细分格式S或细分掩模的生成函数.
给定m重细分掩模a={ai}i∈∈l0(),记suppa={i∈,ai≠0}.若ai=a-i,则称细分掩模或生成函数是对称的. 易知生成函数是对称的当且仅当).若对称的细分掩模满足
则对应的细分称为插值型细分,否则称为逼近型细分.

(1)

Jia[13]指出,给定有限支撑的细分掩模{ai}i∈,则对任意多项式q(x),下两式等价:


众多学者研究从逼近型细分构造插值型细分的问题,其中一大类方法是借助于顶点处的偏移量.偏移量是若干同层相邻顶点的线性组合,且线性组合的系数和为0. 将偏移量加在同层顶点的仿射组合后,可以起局部调整的作用. 这种局部调整作用在从逼近型细分到插值型细分的转变过程中起关键作用. 檀结庆等人[11]发现,许多已有的逼近细分也可看作是插值型细分加上偏移量构造出的. 例如三次B样条细分格式
可看作是插值型格式

借助于此思想,檀结庆等人[11]将Hassan[12]的三重插值型细分格式
(2)
通过加入偏移量,得到了新的逼近型格式
(3)

2 主要结果
讨论添加偏移量构造的细分格式能否达到的最高阶求和规则.











证毕.
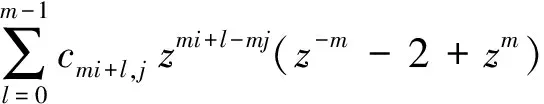



上面是在讨论能否构造出具有最高阶求和规则的细分. 实际上,也可从具有最高阶求和规则的细分出发,通过降低求和规则阶数,将因式1+z+…+zm-1进行某种对称形式的扰动,令其满足如插值等其他性质,从而获得新的细分生成函数.
Maximal sum rule orders of subdivision schemes based on offset vectors
QIWanfeng,WANGJinling
(School of Mathematics, Liaoning Normal University, Dalian 116029, China)
Subdivision method is an important curve and surface modeling tool, and is widely used in many fields as it has numerous advantages. Sum rule is an important property of subdivision schemes. This property is closely related to the convergence property, smoothness order, polynomial generation property, and approximation order of a subdivision scheme. Adding offset vectors is an essential tool to construct new subdivision schemes. However, little attention has been paid to the maximal order of sum rules of subdivision schemes that are constructed via adding offset vectors.For symmetric generating functions, if the support of the added offset vectors includes that of the initial generating function, then the subdivisions scheme with maximal order of sum rule order can be obtained.The maximum sum rule orders of subdivision schemes which are constructed from given subdivisions plus some offset vectors are investigated. If the initial subdivision scheme satisfies sum rules of order two, then the initial subdivision scheme plus linear combinations of the second order difference quotients can also achieve the maximal sum rule orders.
subdivision scheme;sum rule order;offset vector;second order difference quotients
2016-09-10 基金项目:国家自然科学基金资助项目(61502217);辽宁省教育厅科学研究一般项目(L2014428) 作者简介:亓万锋(1984-),男,山东临沂人,辽宁师范大学讲师,博士.
1000-1735(2017)01-0014-06
10.11679/lsxblk2017010014
TP391
A

