一类多时滞切换随机系统的无源输出调节问题

李莉莉, 苑春波, 史宁宁, 周月峰

(辽宁师范大学 数学学院， 辽宁 大连 116029)

一类多时滞切换随机系统的无源输出调节问题

李莉莉, 苑春波, 史宁宁, 周月峰

(辽宁师范大学 数学学院， 辽宁 大连 116029)

基于无源性讨论一类多时滞切换随机系统的输出调节问题.构造分段Lyapunov泛函,利用平均驻留时间方法,分别设计多时滞全息反馈控制器和多时滞误差反馈控制器.结合自由权矩阵方法和詹森积分不等式,以线性矩阵不等式的形式给出多时滞切换随机系统的无源输出调节问题可解的充分条件.最后,用两个仿真例子说明结果的有效性.

切换随机系统;多时滞;输出调节问题;无源性;平均驻留时间

输出调节问题是指通过设计反馈控制器实现闭环系统渐近跟踪参考信号和渐近抑制扰动信号的同时,保持闭环系统内部稳定,是控制领域的一个十分重要的课题.基于凸组合方法给出了一类线性切换系统输出调节问题的可解性条件[1].为进一步降低保守性,利用多Lyapunov函数方法研究了离散线性切换系统的输出调节问题[2].研究了具有切换外部系统的线性系统输出调节问题,但系统本身是非切换系统[3].基于多Lyapunov函数和平均驻留时间两种方法给出了几类切换系统输出调节问题可解的条件[4].基于中心流形理论讨论了非线性时滞系统输出调节问题可解的条件[5].但到目前为止, 对于多时滞切换随机系统输出调节问题的研究成果尚未见报道.又因无源性理论定义的存储函数与系统能量紧密相关, 所以常将存储函数作为系统的Lyapunov函数用以分析系统稳定性.受此启发,笔者将以无源性为工具, 基于平均驻留时间方法,结合自由权矩阵和詹森积分不等式,给出调节器和切换信号设计方案,保证多时滞切换随机系统的输出调节问题可解.最后,用数值例子说明结果的有效性.

1 问题描述与预备知识

考虑如下形式的一类多时滞切换随机系统:

(1)

其中，x(t)∈n为状态,h0=0,hj≥0(j=1,2)是常时滞为定义在m维完备概率空间上的布朗运动且满足E{dw(t)}=0和E{dw(t)2}=dt,z(t)是控制输出,切换规则σ(t):是分段常值函数,ui(t)∈m为第i个子系统的控制输入,φ(θ)是[-h,0]上的一个向量值初始函数,fi∈n×m是以非线性函数形式存在的随机扰动,Aji,Bi,Ci,Fji为适当维数的常矩阵,v(t)∈L2[0,+∞)是外部输入变量,满足外部系统

dv(t)=Sv(t)dt.

(2)

为了考虑系统(1)的输出调节问题,做如下假设:

假设1[6]存在实常阵G0i,G1i,G2i使

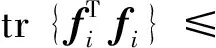
结合假设2, 系统(1), 系统(2)在全息反馈控制器

(3)

下的闭环系统为

(4)

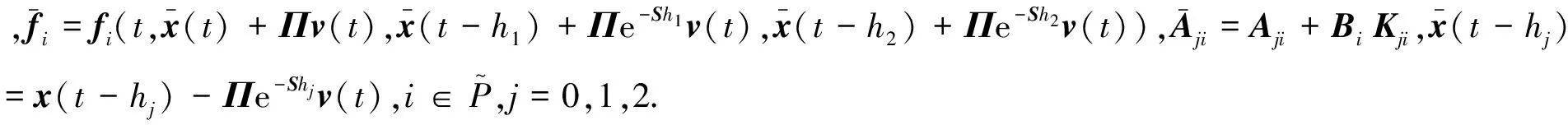
结合假设3,系统(1), 系统(2)在误差反馈控制器

(5)

下的闭环系统为

(6)

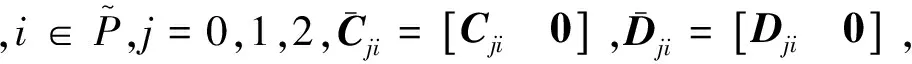
为解决本文涉及的问题,给出一些相关定义和引理．

定义1[4]令Nσ(t,T)表示切换信号σ(t)在[t,T]上切换次数,T>t>0.如果存在N0≥0和Ta>0,使得Nσ(t,T)≤N0+(T-t)/Ta成立,则Ta称为平均驻留时间.通常取N0=0.

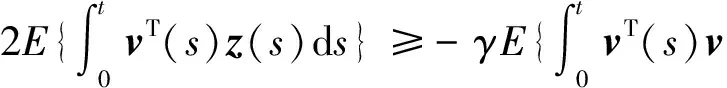
引理1[6](詹森积分不等式)对于任意的常数矩阵Z=ZT>0，标量h>0和向量函数x(·):[-h,0]→n使得成立.

2 全息反馈输出调节问题

给出系统(1)在全息反馈控制器(3)下的闭环系统(4)的随机无源输出调节问题可解的充分条件.

定理1 若假设1和假设2成立,并且对于给定的常数0=h0≤h1≤h2,α>0和μ≥1,存在矩阵Pi>0,Qji>0,Zji>0，适当维数矩阵K0i,K1i,K2i, 对称可逆矩阵Ti以及标量γ>0,εi>0使得

(7)

Pi≤εiI,

(8)

(9)

则存在全息反馈控制器(3)和满足平均驻留时间条件

(10)

的任意切换信号,使得系统(1)的输出调节问题可解,其中，

证 构造如下Lyapunov泛函

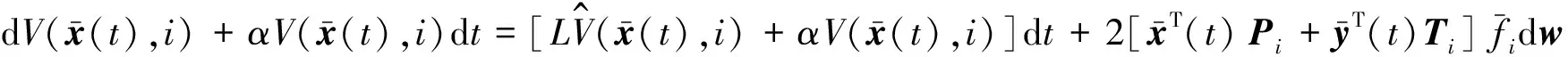
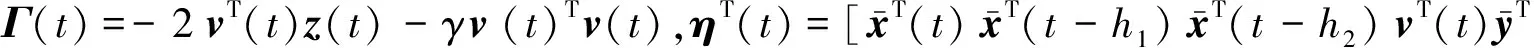
在t∈[tk,tk+1)上,对该式两端同时积分之后取期望得到

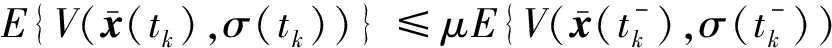
(13)

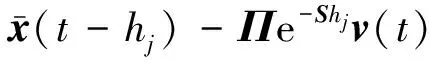
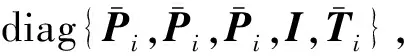
(14)

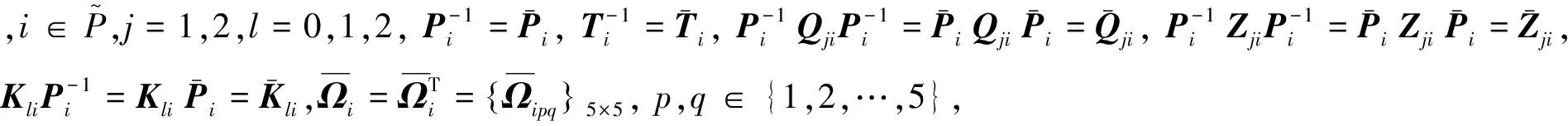
3 误差反馈输出调节问题

给出系统(1)在误差反馈控制器(5)下的闭环系统(6)的随机无源输出调节问题可解的充分条件.

(15)

(16)

(17)

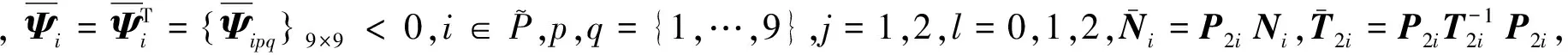
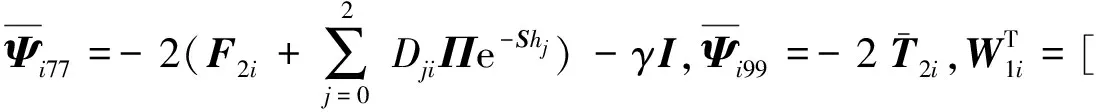
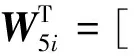
证 选取Lyapunov泛函

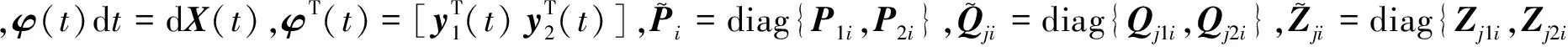
4 数值例子

例1 考虑含有2个子系统的切换系统, 其中，

取满足假设2的矩阵

图1 切换策略

图2 闭环系统的状态响应和输出误差

例2 考虑含有2个子系统的切换系统，其中，

取满足假设3的下列矩阵

图3 切换策略

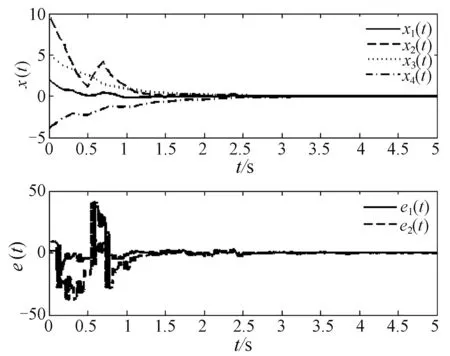
图4 闭环系统的状态响应和输出误差

5 结 论

基于平均驻留时间方法,以无源性为工具研究一类多时滞切换随机系统的输出调节问题.结合自由权矩阵方法和詹森积分不等式,设计切换规则和全息、误差两种反馈控制器,以线性矩阵不等式的形式给出了输出调节问题可解的充分条件.

[1] LIU Y,ZHAO J.Output regulation of a class of switched linear systems with disturbances[C].American Control Conference, Arlington VA,2001:882-883.

[2] 宋政一,聂红,赵军.线性离散切换系统的输出调节问题[J].控制与决策,2006,21(11):1249-1253.

[3] GAZI V.Output regulation of a class of linear systems with switched ecosystems[J].International Journal of Control,2007,80(10):1665-1675.

[4] 董潇潇.切换系统的输出跟踪与调节问题的研究[D].沈阳：东北大学,2012.

[5] FRIDMAN E.Output regulation of nonlinear systems with delay[J].Systems & Control Letters,2003,50(2):81-93.

[6] LIAN J,SHI P,FENG Z.Passivity and passification for a class of uncertain switched stochastic time-delay systems[J].IEEE Transactions on Cybernetics,2013,43(1):3-13.

Passive output regulation problem for a class of switched stochastic systems with multi-delays

LILili,YUANChunbo,SHINingning,ZHOUYuefeng

(School of Mathematics, Liaoning Normal University, Dalian 116029, China)

This paper discusses the output regulation problem for a class of switched stochastic systems with multi-delays based on passive performance.Constructing a piecewise Lyapunov functional and using the average dwell time method, a full information feedback controller and an errorfeedback controllerare designed with multi-delays respectively.By combining the free-weighting matrix method and Jensen’s integral inequality, sufficient conditions for the solvability of the passive output regulation problem for switched stochastic systems with multi-delays are given in the form of linear matrix inequalities.Besides, two simulation examples are introduced to illustrate the validity of the results gained.

switched stochastic systems;multi-delays;output regulation;passivity;average dwell time

2016-09-20 基金项目：国家自然科学基金资助项目(61304056；11671184)；大连市高层次人才创新支持计划项目(2016RQ049) 作者简介：李莉莉(1982-)，女，辽宁大连人，辽宁师范大学副教授，博士．

1000-1735(2017)01-0006-08

10.11679/lsxblk2017010006

TP273

A