掷出的数学智慧——数学活动经验的有效累积*

福州教育学院二附小 朱顺进

掷出的数学智慧
——数学活动经验的有效累积*

福州教育学院二附小 朱顺进

小学数学课程标准将“双基”发展为“四基”，即小学数学教学不仅要重视基础知识、基本技能的传授，还要关注数学基本思想的渗透以及学生基本活动经验的积累。如何有效引导学生掌握有用的活动经验，成为亟待解决的问题。猜想、探究和验证是一种有效数学活动的模式，该文以“掷一掷”一课教学为例，探讨如何让小学生在课堂中获得数学活动经验。

数学活动经验 有效累积 小学数学

《掷一掷》是一节以游戏形式探讨可能性大小的综合实践活动课，数学味道浓，学生有具体操作和探究的过程，可以说是教授学生如何获取活动经验的适当时机教学。如何有效地引导在活动中获取有用的活动经验，成为最急需解决的问题。

1 从已有经验入手，精心创设情境

新《标准》提出，数学教学活动应该是从学生的生活经验出发，必须建立在学生的认知发展水平和已有的知识经验基础之上。

师：如果掷一个骰子，可能会出现几？

生：1到6都有可能。

师：如果同时投掷2个骰子，数字之和可能是几？

生：6、8、12……

师：和可能是几到几？

生：可能是2-12之间的任一个数。

师：掷出的和是1有没有可能？

师：13呢？

……

掷一个骰子可能会出现数字几，这是学生已熟知的，面朝上的点数只可能是1～6中的一个。而一起掷两个骰子和的情况，三年级的学生大都能说出一两种，所有的情况无法一下说出，这时“和可能是几到几？”“掷出的和是1有没有可能？13呢？”等的追问，给学生不同层次的提问，逐步引导学生向深层思考。“和是2～12之间的任一个数都有可能。和最大是12，最小和是2”的回答接踵而至。恰当的追问，合理的引导，可以使学生对骰子的认识，从玩具、六面、一到六个孔（或数字）的初级层面，提升到对和组合的关注。

根据生产过程的特点，将制造资源划分为特征资源和辅助资源两大类。其中，特征资源指根据制造活动执行必需的资源对象，如生产状态、刀具、毛坯、工艺方案等；辅助资源指除了特征资源以外的所有资源。约束条件包括生产过程中影响制造活动执行的各类条件等。

动画演示：喜羊羊提议：“我们同时投2个色子，如果和是2、3、4、10、11、12这6个数，你灰太狼赢；如果和是5、6、7、8、9这5个数字，我喜羊羊赢，可以吗？”

师：这么比，谁赢的可能性大呢？

生：灰太狼赢的机会大。

“掷两个骰子，到底哪些和出现的次数比较多？”这个问题却是学生平时不曾关注的，是骰子熟悉面孔下陌生的一面。学生根据已有的经验：多，赢的可能性就大，大多数学生得出“灰太狼拿的和多，赢的机会就大”的猜想。也有少数学生认为喜羊羊赢的可能性更大，但无论是认为“灰太狼赢的可能性大”还是认为“喜羊羊赢的可能性大”，学生的想法都只停留在猜测层面，这样的猜测表面看似合情合理，实际上学生并没有必胜的把握，气壮却理不直，实则都没有充分的把握来说服对方。这样就给后续的验证埋些伏笔，为学生“我要探究”提供动力。

2 猜想验证不是“一条道走到黑”

猜想、验证阶段需要反复调整思考的方向、思辨过程的合理性，不断调整验证的方向。因此，让学生经历猜想、验证、思辨、调整、再验证、再猜想……的过程，这是探究的基本方法，也是有效开展数学活动的一条重要经验。

2.1 动手实践，验证猜想

师：看来也有同学认为这个规则对灰太狼赢的可能性大，有的同学认为喜羊羊赢的可能性大，不过这些看法都只是一种猜测，那到底结果会是怎样呢？我们还是通过实验来验证吧！

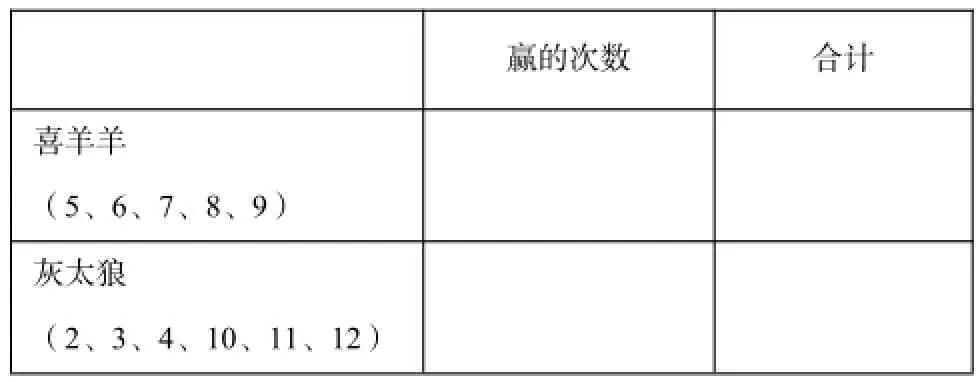
赢的次数合计喜羊羊（5、6、7、8、9）灰太狼（2、3、4、10、11、12）

任何猜想都要经过验证，如果只有猜想而没有验证，那只能是空想，要验证猜想是否正确，光靠争论和感情是不起作用的，要想知道猜想的对错，就要开展实验活动，在这种思维驱使下，每个学生都会主动参与到掷骰子、记录、填表、汇报、观察和发现的全过程，不走过场，体验深刻。

2.2 示范活动流程，渗透随机思想

《数学课程标准》指出，“有效的学习活动不能单纯地依赖模仿与记忆，动手实践、自主探索与合作交流是学习数学的主要方式”。自主不等于放手，适当的引导才是活动有效开展的保证。因此，活动示范，随机思想的渗透，都使的活动有的放矢，不空洞。

师：和是几？谁赢？（演示填表过程）

师：好，如果老师请这位同学再投一次，你觉得和可能是几？可能谁赢？

师：为什么5、6、7、8、9出现次数会比较多呢？

师：如果投出的和是5，骰子1和骰子2分别可能是几和几？

生：1和4,2和3……

师：谁能将所有的可能按一定的顺序说出来？

师：那如果想掷出的和是2、3、8、9……骰子1和骰子2又分别是几呢？

和的组合共有（）种

和骰子1骰子2

师：看了和组成的情况，你有什么想说的吗？

在这节课中，学生亲身经历了解决问题的全过程：猜想、实验、验证、调整和概括结论，这个过程是学生通过活动得到第一收获，老师不可越俎代庖。第二，知识的学习固然重要，而以知识学习为载体的渗透数学思想、方法更重要。《数学课程标准》在总体目标中提出，“通过义务教育阶段的数学学习，使学生能够“获得适应未来社会生活和进一步发展所必需的重要数学知识（包括数学事实、数学活动经验）以及基本的数学思想方法和必要的应用技能。”所以，课堂上，笔者适时地渗透了分类讨论、数形结合、有序思考、概率随机等思想方法。第三，经历探究的全过程，学生对骰子的认识从表面走向深入：当投一个骰子时，选择的数字越多，赢的可能性就越大；当同时投两个骰子时，赢的可能性大小与选择数字的多少没有直接联系，要看和的组合等等。

3 重视回顾，讲求学会策略

师：这节课，大家回想下，从最开始“肯定的支持灰太狼”到后面的质疑，最后得出喜洋洋获胜的可能性大，这一个戏剧性的转变，如何产生？

生：动手试一试。

师：是的，猜想是得到真理的开始，验证是得到真理的必然之路。

经验看似一个虚无的东西，实际上是有步骤的。活动课，热闹是表面，讲求热闹背后的严谨探究。结论固然重要，更重要的是得到知识的过程和思考问题的策略。只有让学生懂得在面对陌生问题时如何去解决，这才是教给学生的“本领”。学生对知识不是一张白纸，也不是零起点，教师适时引导，让学生经历猜想、探究和验证这样一种有效数学活动的模式，体悟到探究问题的“反复”，获得探究的快乐，这样学生就能逐步从陌生变成熟悉，从按部就班到灵活调整，使得探究的“战略”既有固定指导思想，又有灵活“战术”。当然，一个经验的掌握和固化，不是一节课能做到的，需要在适合的课型、适合的问题上，经常运用，有目标地放手运用，才会让学生收获“以渔捕鱼”的本领。

[1]催玉海.获得数学活动经验的四个不等式[J].教学与管理，2012（10）：36-37.

[2]吴良标.把握学生积累数学活动经验的教学时机[J].教学与管理，2015（5）：49-50.