基于贝叶斯网络的航班保障服务时间动态估计

2017-04-17 05:13邢志伟唐云霄

计算机应用 2017年1期

关键词：估计值贝叶斯航班

邢志伟，唐云霄，罗谦

(1.中国民航大学电子信息与自动化学院，天津 300300； 2.中国民航局第二研究所信息技术分公司，成都 610041)

(*通信作者电子邮箱534342497@qq.com)

基于贝叶斯网络的航班保障服务时间动态估计

邢志伟1*，唐云霄1，罗谦2

(1.中国民航大学电子信息与自动化学院，天津 300300； 2.中国民航局第二研究所信息技术分公司，成都 610041)

(*通信作者电子邮箱534342497@qq.com)

针对航班保障服务时间估计的问题，考虑到航班保障服务流程的特殊性、复杂性以及影响因素的不确定性，提出了一种基于贝叶斯网络(BN)的航班保障服务时间估计模型。该模型把航空领域的专家知识与历史数据的机器学习相结合，使用贝叶斯网络的增量学习特性动态地调整BN模型，使其适应新的变化，进而不断更新航班保障服务时间的估计值。使用国内某大型枢纽机场信息系统内提取的数据，通过期望最大化(EM)方法对模型进行训练,得到了测试结果。实验结果分析与模型评价表明,所提方法能有效估计航班保障服务时间且具有较高的准确度。敏感性分析表明，航班到达时段的航班密度对航班保障服务时间影响最强。

航班保障服务；机器学习；贝叶斯网络；增量学习；期望最大化；敏感性分析

0 引言

航班延误一直是困扰民航发展的瓶颈问题。据统计，航班保障服务是影响航班延误的主要因素,对于航班保障服务环节, 目前国内外的研究成果大多集中在仿真分析、调度优化或者流程优化, 而对航班保障服务时间估计的研究极少涉及。Garcia等[1]提出了基于Agent的航班地面保障服务调度分布式控制方法，优化了其调度过程。Andreatta等[2]提出了一种快速启发式方法对航班保障设备和人员进行优化分配，提高了保障服务的效率。郝静麒等[3]用改进的离散事件仿真策略与动态分配法研究平台车资源分配问题。黄鹂诗[4]对机坪车辆进行仿真研究，使用SIMIO 软件实现了保障设备的仿真，但是其研究未考虑车辆的损坏率。Cheung等[5]提出了航班过站保障设备调度的遗传算法并用此算法优化了清水车与拖车的调度，但此算法未考虑保障设备的容量约束。在仿真平台Service model上实现了平台车资源的货物装卸流程仿真，孙瑞山等[6]用关键路径法(Critical Path Method, CPM)研究航班保障服务工作，找出了对保障服务有较大影响的几种服务项目并提出三点建议。为保障服务正常进行提供了参考，但其定量分析有待丰富。丁建立等[7]选取航班过站实际运行的历史数据，采用最大似然估计进行贝叶斯网参数学习来估计航班过站时间，取得了较好的效果，但此方式仅对完备数据集效果明显，处理缺失或稀疏数据时会产生较大偏差。

基于以上分析，本文着眼于航班保障服务时间估计这一国内外学者极少涉及但又具有实际研究意义的课题，以更小的尺度对航班过站的细节进行研究，以提高航班保障效率，减少因航班保障引起的延误。鉴于航班保障服务过程的特殊性、复杂性以及影响因素的不确定性，在研究方法上本文基于贝叶斯网络(Bayesian Network, BN)重点研究对航班保障服务时间的动态估计。贝叶斯网络具有对历史信息要求低、可以进行信息不完全或不确定情况下的推理、可理解性和逻辑性良好、推理结果说服力强等优点，通过构建航班保障服务时间BN模型，不断地对历史数据进行机器学习，动态调整BN模型来估计航班保障服务时间。实验结果分析和模型评价表明本方法能有效估计航班保障服务时间。为机场及其相关部门的应急指挥管理提供及时的预警信息，从而减少因保障环节引起的负面影响，降低旅客极端事件的发生率。

1 航班保障服务分析

1.1 航班保障服务流程分析

单个航班保障服务作业流程可以大致抽象为图1所示，根据对作业流程的分析，可以将保障作业分为航食服务、客舱清洁服务、货舱服务、加油服务、机务巡检5个并行工作流程，某些并行工作流中又包含串行子工作流。各项服务工作间不仅有一定的先后关系而且还存在逻辑次序，共同构成了航班保障服务作业流程。在航班保障服务过程中，保障服务车辆都应该及时到位且按规定次序进行服务作业，如果某种特种车辆到位不及时，将造成某项服务的延误，进而波及后续服务作业，产生延误波及效应[8]。保障调度人员在进行调度特种设备时，需要考虑飞机对机场特种设备占用的排它性和航班过站时间的约束性。参与服务的特种车辆需要考虑航班时刻、机型、数量数以及保障服务车辆的行驶路径等因素，因此，航班保障服务作业会受到资源数量的限制。总之，航班保障服务作业一个多种设备动态协作、服务流程串行与并行共存、对资源的时间与空间要求严格的问题。其他方式建模时，不仅数学语言表达或者量化这些复杂关系比较困难，而且往往很难得到准确值。贝叶斯网络的优越性恰能弥补它们的不足，实现对航班保障服务时间的动态估计。

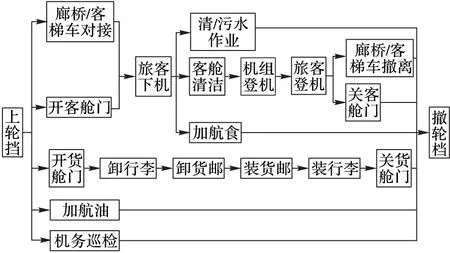
图1 航班保障服务作业流程

1.2 航班保障服务时间影响因素分析

根据机场实际运行数据，本文采用因子分析(Factor Analysis)法[9]对影响航班保障服务时间的各种因素进行了初步筛选，从中得到5个能产生较大影响的因素。

1) 前项服务延误时间。由航班保障服务流程特性分析可知，航班保障服务包含大大小小几十种服务项目，各项服务之间先后关系与逻辑关系并存，串联流程与并联流程共存。它们井然有序的进行是航班保障服务顺利完成的前提，但如果种种因素导致某项服务未按规定完成，将导致后续服务无法正常进行，最终导致航班延误，并且服务延误发生越早，对整个保障过程的影响越严重。

2) 保障资源量。机场在投入使用之前，会按预计吞吐量和起降航班数量对保障设备数量进行估计，寻求一个既能满足民航局文件规定的保障服务时限又能节约资源经费的设备量最优值。在实际运行过程中，设备的损坏、更新以及增添都将直接影响保障服务时间，增添和更新设备利于保障服务，设备损坏则易使保障服务无法按时完成。

3) 航班密度。机场每天的航班密度明显存在波动。高密度情况下，有限的保障设备将连续提供服务，服务项目产生延误的几率也随之升高。反之，低密度时保障设备充足，可以满足保障服务需求，保障服务就可能提前完成。

4) 机型差异。民航局制定的《机场航班运行保障标准》按飞机座位数将机型分类，E类：351座以上；D类：251～350座；C类：151～250座；B类：61～150座；A类:60座以下。座位数越多的机型保障服务占用的时间越久，因此，集中到港的大机型将长时间占用保障设备，致使其他航班等待某项服务的时间延长，从而保障服务时间延长。

5) 旅客因素。按照标准，航班停放近机位时，登机口关闭时间不应晚于航班计划关舱门时间/预计关舱门时间前5 min。航班停放远机位时，不应晚于航班计划关舱门时间/预计关舱门时间前10 min。因此，晚到的旅客即使能够在顺利登机，也会使得关舱门时间推迟。

其他因素产生的影响可由机场、航空公司、空管等部门的协作解决，故本文将此部分因素忽略不计。

2 航班保障服务时间估计BN模型

2.1 贝叶斯网络概述

贝叶斯网络(BN)，又称有向无环图模型，是一种概率图模型。有向无环图(Directed Acyclic Graph, DAG)中节点集X={X1,X2,…,Xi}表示一组随机变量，节点间的有向边(弧)代表了节点间的互相关系。条件概率分布(Conditional Probability Distributions, CPD)表示随机变量之间的关联强度。一个BN可由B(G,P)表示，其中G=〈X,A〉表示由个节点组成的DAG，A表示有向边(弧)的集合，P={P(Xi|parent(Xi))}表示任意节点的CPD，parent(Xi)表示X中所有父节点的集合。此外，条件独立性假设描述如下: 有节点X1、X2和X3，若P(X1|X2X3)=P(X1|X2)，则称X1和X3在X2条件下独立、X1在X2条件下独立于X3，或X1和X3关于X2独立。“条件独立” 是BN中隐含的断言(assertion)和假设(assumption)，BN结构决定于式(1)所示的条件独立性假设：

P(Xi|X1,X2,…,Xi-1)={P(Xi|parent(Xi))}

(1)

由概率的链式法和条件独立性假设则可知其联合概率分布的表示形式如式(2)所示：

(2)

2.2 航班保障服务时间BN模型

构建BN的方法大致有以下几种：1)数据学习：通过大量样本数据的机器学习，实现贝叶斯网络的结构和参数学习。2)专家知识：基于领域专家明确各个变量之间的依赖关系,从而确定BN结构并指定其分布。3)综合方法：结合专家知识与数据学习两种方法，先由相关领域专家知识指定网络结构，再由机器学习方法从大量样本数据中学习网络参数。

方法1)要求大量样本作为训练数据，这在缺少样本或样本量较少情况下不适用。方法2)在缺乏样本数据且专家定性知识宝贵的情况下较为适用，但其主观性强，容易产生大的误差。方法3)是前两种方法的有机结合，可以提高学习的效率。由本文1.2节分析可知，航班保障服务样本数据变量之间有明显的依赖关系。故为了提高学习效率、减小误差，本文采用方法3)进行BN构建。通过对中国民航领域相关专家进行走访和调研，确定了航班保障所需各类节点及其状态、节点间的独立或者依赖关系。先验的BN拓扑结构如图2所示。

图2 航班保障服务时间BN拓扑结构

变量集为X={X1,X2,X3,X4,X5,X6}，其中X1～X6分别表示机型影响、前一项服务延误时间(单位为min)、保障设备、旅客因素、航班密度、航班保障服务时间(单位为min)。各变量含义为：

X1={A,B,C,D,E},其中A、B、C、D、E表示飞机类型。

X2={<2,[2,4),[4,6),[6,8),[8,10),[10,12],>12}。

X3={Eq1,Eq2,Eq3,Eq4,Eq5,Eq6,Eq7,Eq8,Eq9}，其中Eq1～Eq9分别表示客梯车、清水车、污水车、清洁车、食品车、加油车、传送带车、摆渡车、行李车。

X4={ontime,delay}，表示旅客是否准点到达。

X5={density1,density2,density3,density4}，density1～density4分别表示非常稀疏、一般稀疏、一般密集、非常密集。

X6={<20,[20,30),[30,40),[40,50),[50,60),[60,70),[70,80),[80,90],>90}。

2.3 参数学习

参数学习指已知网络拓扑结构，需要明确网络参数的过程。多种算法可以实现参数学习，常用算法包含极大似然估计(MaximumLikelihoodEstimation,MLE)、期望最大化(ExpectationMaximization,EM)方法、贝叶斯估计(BayesianEstimation)和梯度下降(GradientDescent,GD)法等[10-13]。对于样本所使用的学习算法性能优劣，主要根据其学习精度和速度判断。其中极大似然估计主要应用于完备数据集，而期望最大化方法主要应用于不完备数据集的参数学习且算法稳定，实现简单。由于航班保障服务过程复杂，所涉及的保障车辆种类繁多，因此，在各方面或多或少的因素制约下，航班保障服务过程中会不可避免地产生部分数据缺失的情形，从而使得对数据观测后形成不完备数据集，所以本文使用EM方法来对训练样本进行参数学习。图3给出不完备数据处理流程。

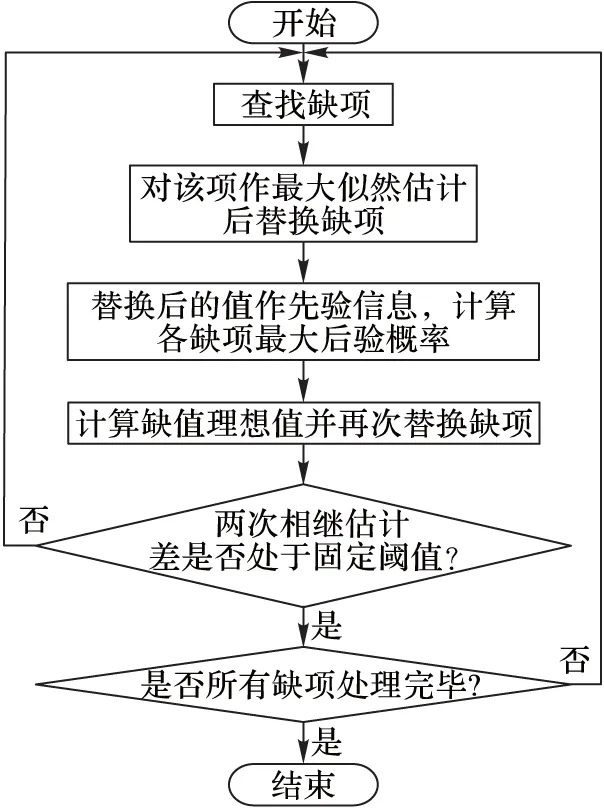
图3 不完备数据处理流程

假设D={D1,D2,…,Dn}表示一组缺值样本数据集；Z={Z1,Z2,…,Zn}表示隐藏数据集；Xi表示Di中缺值样本；θi表示参数θ的当前估计，定义基于Di的θ对数似然函数如式(3)所示：

(3)

EM方法使用迭代方式循环交替地执行E步和M步：E步基于当前的参数估计，计算它的期望值；M步基于E步参数的期望值，最大化当前的参数估计。第i+1次迭代时E步：

(4)

M步:

Q(θi+1|θi,D)=maxQ(θ|θi,D)

(5)

式中P(θ|D)、P(θ|D,Z)、P(Z|θi,D)分别为参数θ的基于D的后验分布密度，增加隐藏数据后的后验分布密度，在给定θ和D时Z的条件分布密度。循环迭代至‖θi+1-θi‖足够小为止。

2.4 航班保障服务时间动态估计

随着时间的增加，航班保障服务相关数据逐渐积累，若要使动态估计更加准确，需要将新数据不断地加入到训练集中，动态调整BN模型，从而产生新的先验知识。由领域专家以及数据结构学习获得的先验知识结合参数学习形成BN模型，此过程又称为知识获取。图4给出航班保障服务时间动态估计流程。

由图4可知由模型产生的新知识又将作为先验知识为BN学习提供参考。此过程可由贝叶斯法则实现，式(6)[14]为其数学表达：

(6)

其中：D表示训练样本数据集；h表示某种假设。P(h)表示h的先验概率,P(D) 表示样本数据集D的先验概率,P(D|h)表示假设h成立时D的概率。P(h|D)表示给定D时h成立的概率, 也称h的后验概率。应当明确的是：先验概率P(h)独立于D而后验概率P(h|D)反映了D的影响。

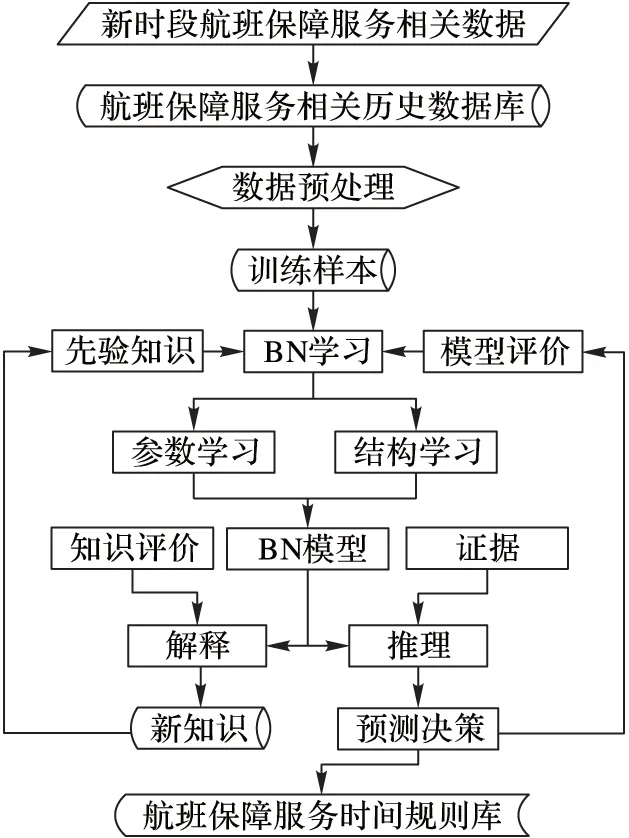
图4 航班保障服务时间动态估计流程

这就使得BN模型可以连续调整，从而适应新的变化。这种通过BN学习动态修正模型的方式可以动态估计航班保障服务时间。

3 实验与分析

3.1 实验结果及分析

实验数据来源于国内某大型枢纽机场信息系统数据库，提取了该机场2015年5月至2015年10月的航班保障服务相关数据，共计36万多个，经过初步处理筛选出对航班保障服务有影响的数据。数据包括航班班次信息、工作任务及相关时间特性三大类。其中班次信息数据包含航班号、所停机位号，工作任务包括客舱清洁、开关客舱门、航油加注、机务巡检、装卸货邮、航食配送、放撤轮挡、上下乘客，相关时间特性包括参与保障作业的特种车辆或人员的到位时刻、等待时间、作业时间、结束时刻。

数据不可避免地存在小部分缺失或者稀疏情况，因此对这些不完备数据按图3所示流程进行处理。然后用2015年5月至2015年9月期间处理完成后的20万多个数据作为学习的样本数据。参数估计采用加拿大Norsys软件公司的NeticaTutorial工具的参数学习功能完成。Netica软件对于贝叶斯网络和影响图功能强大，操作简单，具有直观且流畅的用户界面用于绘制网络，一旦网络被创建，Netica可以使用网络来执行最快、最现代化的算法进行各种推理，发现所有的未知变量的相应值或概率。Netica的参数学习采用服从狄氏共轭先验分布的多项式随机变量。使用步骤简述如下：1)搭建贝叶斯网络；2)导入数据文件；3)选择训练算法(期望最大化方法)；4)发现未知变量相应值或概率。进行网络学习前通过专家知识直接给定先验概率，使用EM方法进行数据学习之后得到其后验概率，修正先验概率分布，以此产生条件概率表CPT，得到如图5所示的学习结果。根据航班保障服务时间动态估计流程，2015年5月至9月BN学习结果属于新知识，将其视为先验知识后，再用2015年10月数据对BN模型增量学习，图6给出增量学习结果。

图5 2015年5月至9月数据学习结果

图6 2015年10月数据增量学习结果

从图5可看出，前一项服务延误两分钟以内所占比重较高，达到85.7%，说明航班的大部分保障服务项目都会按时完成。航班保障服务的各种设备的占比均衡，使用频率高的设备(Eq7：传送带车)占比稍高于使用频率低的设备(Eq8：摆渡车)。航班密度在density3：一般密集时影响最大，机型C占比也达到51.6%。对比图5和图6可知各变量的概率分布存在微小变化。随着航班保障服务相关数据不断更新，按照图4所示的航班保障服务时间动态估计流程，BN模型可以被连续地调整，从而适应新的变化。令E(t)表示其他条件确定下的航班保障服务时间期望值；Ti表示第i个航班保障服务时间值域的中值；P(i)表示航班保障服务时间落在第i个值域中的概率，则由式(7)的计算方法可以求得确切的航班保障服务时间期望值，此值可被视为航班保障服务时间的估计值。

E(t)=∑P(i)×Ti

(7)

表1给出了部分航班在模型动态调整前后结合BN学习和式(7)得到的航班保障服务时间估计值。为了更直观地显示估计效果，方便分析，图7给出部分航班保障服务时间估计值与实际值对比图。

表1 部分航班保障服务时间估计值与实际值比较

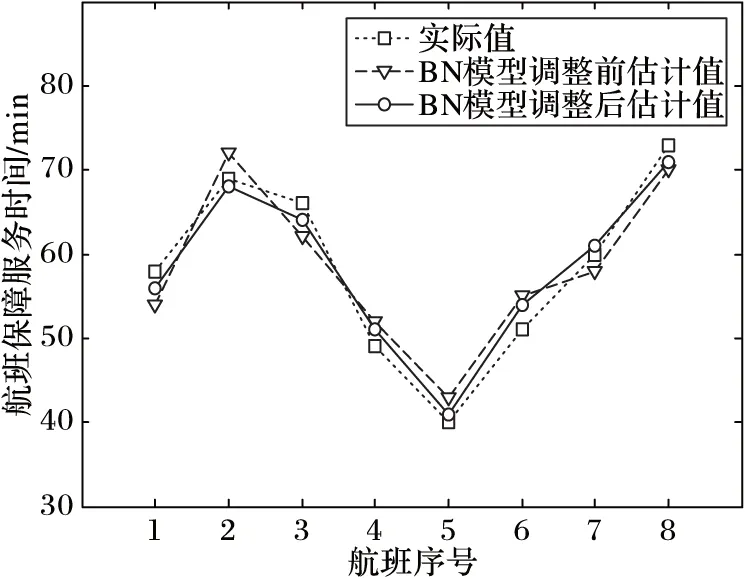
图7 部分航班保障服务时间估计值与实际值对比

表2为《机场航班运行保障标准》规定的各类机型保障作业时间要求。本文保障服务时间指轮挡时间，假如航班保障服务过程耗时不超过标准服务时间，就不会发生因保障服务作业而引起的航班延误。

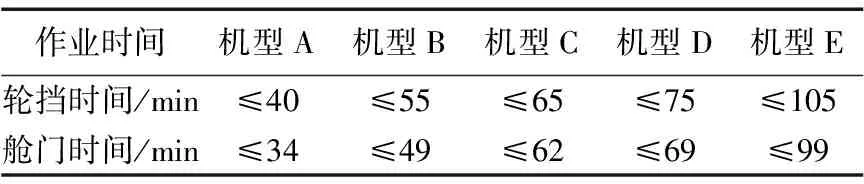
表2 各类机型保障作业时间要求

结合表1～2发现1、3、8号航班机型相同，但是到达时段的航班密度不同，保障服务时间也存在差异，航班密度越大，保障服务耗时越长并导致8号航班未能在按时完成保障服务。这是因为大密度情形下保障设备来不及准时到位。2、3号航班同一时段到达，但机型不同，保障服务耗时也有差异。由图7可知估计值与实际值趋于一致，并且经过贝叶斯网络学习调整后的BN模型估计值与真实值更接近。将在后文模型评价中量化估计值与真实值的误差。

3.2 敏感性分析与模型评价

在航班保障服务时间的影响因素中，各种因素的影响程度是不同的。本文通过对实验结果进行敏感性分析(SensitivityAnalysis,SA)[15]来度量各个因素对航班保障服务时间的影响程度。敏感性分析基于两变量间的互信息(MutualInformation,MI)，由互信息比重来判定影响程度强弱，式(8)给出互信息的定义。

(8)

式中：X表示航班保障服务时间，Y表示其他各种影响因素；x和y分别表示航班保障服务时间及其他各种影响因素的状态；H(X)表示观测X后的信息量，H(X|Y)表示知道Y时信息量；通过I(X;Y)能够判定变量之间的相关性，I(X;Y)≥0，且等号成立的充要条件是X和Y相互独立。I(X;Y)比重越大则表示变量之间相关性越明显，换言之，即某影响因素对航班保障服务时间的影响程度更大。表3给出各种因素相对于航班保障服务时间的敏感性分析结果。

表3 各因素相对航班保障服务时间的敏感性分析结果

从表3中可知各种影响因素与航班保障服务时间互信息占比从大到小分别为是航班密度、保障设备、机型影响、前一项服务延误时间、旅客因素，因此可得航班到达时段的密度对航班保障服务时间影响最强，旅客因素相对于所列其他因素影响最弱。

最后对本文所建的BN模型进行评价。分别将2015年5月至9月以及2015年10月数据当作学习样本，2015年11月数据用来测试，航班保障服务时间节点作为测试节点。通过2015年5月至9月的数据学习及2015年10月的增量学习，得到航班保障服务时间节点的条件概率分布, 计算部分航班的保障服务时间如表1所示，将模型调整前后的估计值分别与实际值对比, 进而评价模型估计的准确性。评价的度量标准选用均方根误差(RootMeanSquareError,RMSE)、平均绝对误差(MeanAbsoluteError,MAE)和希尔不等系数(TheilInequalityCoefficient,TIC)[16]。

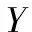
(9)

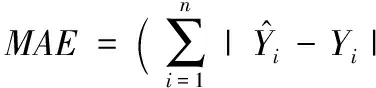
(10)

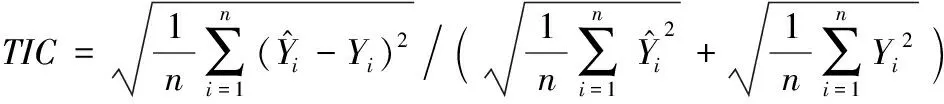
(11)

RMSE对极大或极小误差异常敏感，因此RMSE能够很好地反映估计的精密度。MAE由于离差被绝对值化，不会出现正负相抵消的情况，因而，MAE能更好地反映预测值误差的实际情况。TIC总是介于0至1之间，数值越小则估计值和真实值之间的差异越小，估计精度越高。表4给出部分航班在BN模型调整前后航班保障服务时间估计值的误差统计。

表4 BN模型调整前后估计值的误差统计

从表4可知，由2015年5月至9月数据进行贝叶斯网络学习建立的BN模型(调整前)得到的估计值误差均大于更新先验知识后2015年10月增量学习建立的BN模型(调整后)的估计值误差。本文认为这是由于调整后的BN模型更新了先验知识、学习了最新数据，因此对近期航班保障服务反映能力更强。从各种误差分析方法得到的误差值可以看出，BN模型调整前后均能对航班保障服务进行有效估计且有较高的准确度，说明使用贝叶斯网络对历史数据不断学习进而动态调整BN模型的方式来估计航班保障服务时间可行。

4 结语

本文将贝叶斯网络应用于解决航班保障服务时间估计的问题。建立了其BN模型，阐述了参数学习方法，将数据集导入到软件平台进行训练得到了学习结果。实验结果分析及模型评价表明，所提模型能够实现对航班保障服务时间的动态估计并具有较高的准确度。敏感性分析发现，航班到达时段的密度对航班保障服务时间影响最强，旅客因素相对于所列其他因素影响最弱。由于本文未考虑冬季除冰雪保障环节，因此应用时会存在季节局限性。进一步研究方向包括进一步研究方向包括考虑航班提前或者延误到港情况，提高航班保障时间估计准确度。

)

[1]GARCIAAP,GARCIAHA,OTAMENDIFJ,etal.Agent-baseddistributedcontrolforimprovingcomplexresourcescheduling:applicationtoairportgroundhandlingoperations[J].IEEESystemsJournal, 2014, 8(4): 1145-1157.

[2]ANDREATTAG,DEGIOVANNIL,MONACIM.Afastheuristicforairportground-serviceequipment-and-staffallocation[J].Procedia—SocialandBehavioralSciences, 2014(108): 26-36.

[3] 郝静麒,杨文东,唐小卫.枢纽机场停机坪平台车资源分配仿真研究[J].武汉理工大学学报,2013,35(12):85-91.(HAOJQ,YANGWD,TANGXW.Simulationforplatformtruckresourceallocationinhubairportapron[J].JournalofWuhanUniversityofTechnology, 2013, 35(12): 85-91.)

[4] 黄鹂诗.基于SIMIO的机坪车辆调度仿真研究[D].南京:南京航空航天大学,2013:11-14.(HUANGLS.SimulationstudyofvehicleschedulingonrampbasedonSIMIO[D].Nanjing:NanjingUniversityofAeronauticsandAstronautics, 2013: 11-14.)

[5]CHEUNGA,IPWH,LUD,etal.Anaircraftserviceschedulingmodelusinggeneticalgorithms[J].JournalofManufacturingTechnologyManagement, 2004, 16(1): 109-119.

[6] 孙瑞山,张子仝.基于CPM的停机坪航班保障工作方法研究[J].中国民航大学学报,2011,29(5):23-26.(SUNRS,ZHANGZT.StudyonapronflightserviceworkmethodbasedonCPM[J].JournalofCivilAviationUniversityofChina, 2011, 29(5): 23-26.)

[7] 丁建立,赵键涛,曹卫东.基于贝叶斯网的航班过站时间动态估计[J].南京航空航天大学学报,2015,47(4):517-524.(DINGJL,ZHAOJT,CAOWD.DynamicestimationaboutturnaroundtimeofflightbasedonBayesiannetwork[J].JournalofNanjingUniversityofAeronautics&Astronautics, 2015, 47(4): 517-524.)

[8]XIACY,WANGL,SUNSW,etal.AnSIRmodelwithinfectiondelayandpropagationvectorincomplexnetworks[J].NonlinearDynamics, 2012, 69(3): 927-934.

[9]GREATOREXM.FactorAnalysis[M].Hoboken,NJ:JohnWiley&Sons, 2015: 27-29.

[10] 李硕豪,张军.贝叶斯网络结构学习综述[J].计算机应用研究,2015,32(3):641-646.(LISH,ZHANGJ.ReviewofBayesiannetworksstructurelearning[J].ApplicationResearchofComputers, 2015, 32(3): 641-646.)

[11]MASEGOSAAR,MORALS.Newskeleton-basedapproachesforBayesianstructurelearningofBayesiannetworks[J].AppliedSoftComputing, 2013, 13(2): 1110-1120.

[12]JIJZ,WEIHK,LIUCN.AnartificialbeecolonyalgorithmforlearningBayesiannetworks[J].SoftComputing, 2013, 17(6): 983-994.

[13]BOUCHAALAL,MASMOUDIA,GARGOURIF,etal.ImprovingalgorithmsforstructurelearninginBayesiannetworksusinganewimplicitscore[J].ExpertSystemswithApplications, 2010, 37(7): 5470-5475.

[14]PEARLJ.Onevidentialreasoninginahierarchyofhypotheses[J].ArtificialIntelligence, 1986, 28(1): 9-15.

[15]CASTILLOE,GUTIERREZJM,HADIAS.SensitivityanalysisindiscreteBayesiannetworks[J].IEEETransactionsonSystems,Man,andCybernetics—PartA:SystemsandHumans, 1997, 27(4): 412-423.

[16] 高阳,张碧玲,毛京丽,等.基于机器学习的自适应光伏超短期出力预测模型[J].电网技术,2015,39(2):307-311.(GAOY,ZHANGBL,MAOJL,etal.Machinelearning-basedadaptivevery-short-termforecastmodelforphotovoltaicpower[J].PowerSystemTechnology, 2015, 39(2): 307-311.)

ThisworkispartiallysupportedbytheJointFundsoftheNationalNaturalScienceFoundationofChinaandCivilAviationAdministrationofChina(U1533203),theFundamentalResearchFundsfortheCentralUniversities(3122014P003).

XING Zhiwei, born in 1970, Ph.D., professor.His research interests include equipment and system of civil aviation, information and control of airport traffic.

TANG Yunxiao, born in 1989, M.S.candidate.His research interests include equipment and system of civil aviation, information and control of airport traffic.

LUO Qian, born in 1975, Ph.D., senior engineer.His research interests include airport operation management, data mining.

Dynamic estimation about service time of flight support based on Bayesian network

XING Zhiwei1*, TANG Yunxiao1, LUO Qian2

(1.CollegeofElectronicInformationandAutomation,CivilAviationUniversityofChina,Tianjin300300,China;2.InformationFiliale,TheSecondResearchInstituteofCivilAviationAdministrationofChina,ChengduSichuan610041,China)

Concerning the problems of estimating the service time of airport flight support, and the particularity, complexity, and influence factors’ uncertainty of flight support service process, an estimation model of flight support service time based on Bayesian Network (BN) was proposed.The knowledge of aviation experts and the machine learning of historical data were combined by the proposed model, and the incremental learning characteristic of BN was used to adjust the BN model dynamically, so as to make itself adapt to new conditions and constantly update the service time estimates of flight support.By using the data selected from a large domestic hub airport information system, the proposed BN model was trained via the Expectation Maximization (EM) algorithm to obtain the test results.The analysis of experimental results and model evaluation show that the proposed method can effectively estimate the service time of flight support and has higher accuracy.In addition, the sensitivity analysis demonstrates that the flight density during flight arrival time has the strongest influence on flight support service time.

flight support service; machine learning; Bayesian Network (BN); incremental learning; Expectation Maximization (EM); sensitivity analysis

2016-07-08;

2016-09-05。基金项目:国家自然科学基金委员会-中国民用航空局联合研究基金资助项目(U1533203)；中央高校基本科研业务费基金资助项目(3122014P003)。

邢志伟(1970—)，男，辽宁沈阳人，教授，博士，主要研究方向：民航装备与系统、机场交通信息与控制；唐云霄(1989—)，男，安徽阜阳人，硕士研究生，主要研究方向：民航装备与系统、机场交通信息与控制；罗谦(1975—)，男，四川绵阳人，高级工程师，博士，主要研究方向：机场运营管理、数据挖掘。

1001-9081(2017)01-0299-06

10.11772/j.issn.1001-9081.2017.01.0299

TP181