混沌布谷鸟搜索算法在谐波估计中的应用

牛海帆，宋卫平，宁爱平，马艺元

(太原科技大学 电子信息工程学院，太原 030024)

(*通信作者电子邮箱117632228@qq.com)

混沌布谷鸟搜索算法在谐波估计中的应用

牛海帆，宋卫平，宁爱平*，马艺元

(太原科技大学 电子信息工程学院，太原 030024)

(*通信作者电子邮箱117632228@qq.com)

针对布谷鸟搜索(CS)算法存在后期收敛速度慢、计算精度不高和陷入局部最优等缺点，提出了混沌布谷鸟(CCS)算法。首先，通过混沌理论初始化种群来增加种群多样性；然后，对局部最优值引入混沌扰动算子来跳出早熟收敛，提高计算精度，进而完成全局优化。对4个单目标基准函数进行仿真测试，对比最优值、最差值、平均值、中位数值及标准差值，结果表明，基于CCS算法比CS算法有更快的收敛速度和更高的收敛精度。在电力系统中谐波问题成分引起电流波形畸变，电网不稳定。精确分析谐波成分是解决谐波污染的重要前提。将性能更好的CCS算法应用于谐波估计，通过比较估计均值及标准偏差，结果显示在分析谐波电流时CCS算法相比粒子群优化(PSO)算法具有更好的性能。

粒子群优化算法；布谷鸟搜索算法；混沌理论；函数优化；谐波估计

0 引言

布谷鸟搜索(Cuckoo Search, CS)算法是2009年Yang等[1]提出的。类似于粒子群优化(Particle Swarm Optimization, PSO)算法[2]、遗传算法[3]，是一种新颖的元启发式算法。这种算法源于布谷鸟的巢寄生繁殖机制和鸟类与果蝇的莱维飞行(Levy flight)[4]行为这两个方面。任何优化算法都必然存在优缺点，布谷鸟算法也不例外。为了克服布谷鸟算法在进化后期收敛速度慢、易陷入局部最优等不足，学者们在近几年来努力对其改进并取得了一些成果。2011年Rajabioun等[5]将布谷鸟算法与遗传算法相比较；2013年刘长平等[6]将CS算法与粒子群算法和萤火虫算法进行了测试比较；2014年，Li等[7]将正交法和布谷鸟算法结合；2016年，Uroš等[8]将CS算法与差分进化算法相比较，CS算法均表现其优良的性能。此外，这个算法参数设置少、简单且容易实现，是非常有参考价值的一种优化算法。

近几年来研究者们将布谷鸟算法应用于实际的优化问题中，从单目标优化问题到多目标优化问题，该算法都表现出了良好的寻优能力；如龙文等[9]将一种混合的布谷鸟算法应用于求解约束化工优化问题；孙强等[10]将布谷鸟算法应用于光伏并网中，Lidberg等[11]将其用于制造飞机和燃气涡轮发动机部件的多任务电池的优化等。有许多研究者们将智能优化算法应用于谐波估计中，2002年Macedo等[12]将遗传算法应用于谐波检测中，2012年DE A L Rabelo等[13]将粒子群算法应用于谐波估计中。谐波污染严重影响电力系统的正常运行以及电能的质量，因此，采用布谷鸟算法估计谐波成分具有很高的实用价值。首先，介绍布谷鸟算法的工作原理；其次，对其引入混沌理论，提出了改进的混沌布谷鸟算法；然后，将其应用于谐波估计中，并给出了操作过程；最后，通过实验验证了改进的混沌布谷鸟算法的有效性，并与粒子群算法谐波估计方法进行比较，布谷鸟算法在分析谐波成分时具有明显的优势。

1 布谷鸟搜索算法

布谷鸟采用巢寄生繁殖策略，它将自己的蛋寄放在其他鸟类的巢中让其他鸟类为其孵化。当其他鸟类发现这些外来蛋时，会选择丢弃这些蛋或放弃自己的巢，在其他地方重筑新巢。基于布谷鸟的这种繁殖策略，采用莱维(Levy)飞行方式来更新鸟窝位置，该算法使用以下3个理想规则[14]：

1)每只布谷鸟一次产一个卵，并随机选择寄生巢来孵化它。

2)在随机选择的一组寄生巢中，最好的寄生巢将会被保留到下一代。

3)可利用的寄生巢数量是固定的,一个寄生巢的主人能发现一个外来鸟蛋的概率为Pa。

在以上3个理想规则的基础上，布谷鸟算法采用莱维飞行随机游动来更新鸟巢位置，其更新公式为：

Xg+1,i=Xg,i+α⊕Levy(λ)

(1)

其中：α为步长大小，Levy(λ)为随即搜索路径，服从Levy概率分布。

按发现概率Pa丢弃部分解后，按随机偏好游动产生新的解：

Xg+1,i=Xg,i+r(Xg,i-Xg,k)

(2)

其中：r是区间(0,1)内服从均匀分布的随机数；Xg,i和Xg,k是代表第g代的两个不同的随机解。

2 混沌布谷鸟搜索算法

在基本的CS算法中，采用随机初始化产生初始鸟巢位置，具有较大的盲目性，针对混沌运动的特点，将其运用在优化算法的初始过程中，可以增加种群多样性，提高算法的质量。其次，将混沌扰动算子引入算法的局部最优值中，使算法能够跳出局部最优值。将混沌理论引入布谷鸟算法中，利用混沌理论的特性弥补CS算法在迭代后期收敛速度较慢、收敛精度较低的缺点。

2.1 混沌初始化

混沌状态[15]是自然界中广泛存在的一种非线性现象，具有随机性、遍历性、规律性，对初始条件的敏感性等优点。混沌运动能在一定范围内按其自身的“规律”不重复地遍历所有状态。利用混沌运动的这些特性，可以将其应用于优化搜索。Logistic映射是一种典型的混沌系统，其表达式为：

Xi+1=uXi(1-Xi);i=0,1,2,…,N,u∈(2,4]

(3)

其中，u为控制变量，当u=4时，X0∈(0,1)，Logistic完全处于混沌状态。

混沌初始化的具体过程如下。

步骤1 设置混沌最大迭代次数为M，控制参数u=4，种群规模为N。

步骤2 随机产生D维向量X0=(x01,x02,…,x0D)，其中X0i∈(0,1)且X0i∉{0.25,0.5,0.75}。

步骤3 通过式(3)迭代M次产生M个混沌向量Yi=(yi1,yi2,…,yiD)，i=1,2,…,M。

步骤4 由式(4)产生初始鸟巢位置Xi=(xi1,xi2,…,xiD)：

xij=xmin+yij(xmax-xmin)

(4)

步骤5 计算目标函数，从M个初始群体中选出较优的N个鸟巢位置作为初始鸟巢位置。

2.2 混沌扰动算子

随机产生一个D维向量X0=(x01,x02,…,x0D)，向量的每个元素均是(0,1)区间的随机数。根据式(3)，产生混沌序列X=(x1,x2,…,xD)。

在多维复杂优化问题中，各维之间数值不同，所以各维采取不同的扰动半径。本文采用式(5)确定扰动半径：

(5)

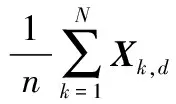
在偏好随机游动更新鸟巢位置后，对最优鸟巢位置添加混沌扰动算子，其方法如下式：

Xnewbest,d=Xbest,d+Rd(2xd-1)

(6)

其中xd为当前代由式(3)产生的混沌序列。

3 布谷鸟搜索算法谐波估计

3.1 谐波估计模型

谐波信号可以用傅里叶级数来表示，各次谐波成分都有各自的幅值和相角，一般的谐波信号波形为：

(7)

其中：x0e-λt是直流衰减成分，λ是时间常数：n表示谐波成分的个数：Ac,i、As,i、θc,i、θs,i正弦和余弦的幅值和相位角：ω0是基波频率。

谐波信号是连续的，这里需要对其采样离散化，其中离散采样个数m要远大于所需估计参数N+1：

其中：k是采样数；Ts是采样时间间隔。

谐波估计的目标函数是均方误差函数[11]：

(9)

其中：em=x(t)-xe(t)，x(t)为估计信号，xe(t)是采样信号；Δ取0.000 01，使得函数EF在最优点有意义。

3.2 CS算法谐波估计的步骤

谐波估计的参数包括3个方面：直流衰减分量的幅值、时间常数和各次谐波的振幅。

CS算法谐波估计的算法代码如下。

Begin混沌初始化N个鸟巢位置：Xi=(xi1,xi2,…,xiD),i=1,2,…,N； 按式(9)计算适应度值f(Xi)； While(不满足结束条件) 采用莱维飞行更新公式(1)产生新的解Xi； 选择候选解Xj； 计算新解的适应度值f(Xi)； If (f(Xi)>f(Xj)) 用新解替代候选解； End

按发现概率Pa丢弃部分解；

用偏好随机游动公式(2)产生新替代丢弃的解；

比较适应度值，保留较优的解Xbest；

用式(3)产生混沌序列；

用式(5)确定混沌扰动区域；

对保留的最优解Xbest按式(6)进行混沌扰动，产生新的解Xi替代任意一个当前代的解； If (f(Xi)>f(Xbest))Xbest=Xi；End

End

End

4 实验结果及分析

4.1 混沌布谷鸟算法的性能

对算法的性能分析采用Matlab2010b来完成，实验中设

定种群规模为30，分别在20,50维对表1中的5个经典单目标测试函数仿真，实验结果在表2～5和图1中显示。最大迭代次数为2 000， β设为0.5，独立运行50次。

表1 测试函数

表2 4个函数运行结果

Tab.2Runningresultsoffourfunctions

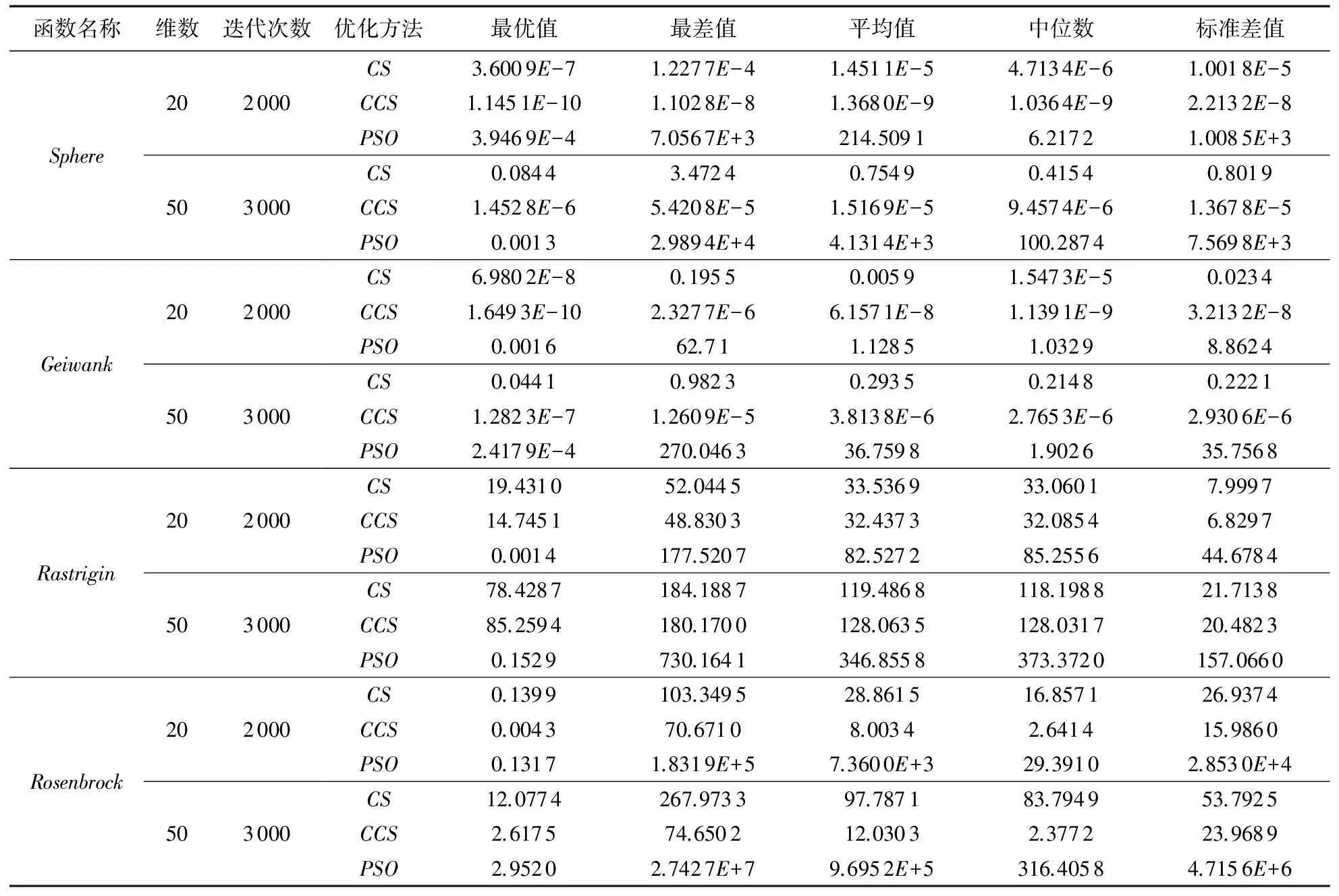
函数名称维数迭代次数优化方法最优值最差值平均值中位数标准差值SphereGeiwankRastriginRosenbrock202000503000202000503000202000503000202000503000CS3．6009E-71．2277E-41．4511E-54．7134E-61．0018E-5CCS1．1451E-101．1028E-81．3680E-91．0364E-92．2132E-8PSO3．9469E-47．0567E+3214．50916．21721．0085E+3CS0．08443．47240．75490．41540．8019CCS1．4528E-65．4208E-51．5169E-59．4574E-61．3678E-5PSO0．00132．9894E+44．1314E+3100．28747．5698E+3CS6．9802E-80．19550．00591．5473E-50．0234CCS1．6493E-102．3277E-66．1571E-81．1391E-93．2132E-8PSO0．001662．711．12851．03298．8624CS0．04410．98230．29350．21480．2221CCS1．2823E-71．2609E-53．8138E-62．7653E-62．9306E-6PSO2．4179E-4270．046336．75981．902635．7568CS19．431052．044533．536933．06017．9997CCS14．745148．830332．437332．08546．8297PSO0．0014177．520782．527285．255644．6784CS78．4287184．1887119．4868118．198821．7138CCS85．2594180．1700128．0635128．031720．4823PSO0．1529730．1641346．8558373．3720157．0660CS0．1399103．349528．861516．857126．9374CCS0．004370．67108．00342．641415．9860PSO0．13171．8319E+57．3600E+329．39102．8530E+4CS12．0774267．973397．787183．794953．7925CCS2．617574．650212．03032．377223．9689PSO2．95202．7427E+79．6952E+5316．40584．7156E+6

在固定的收敛次数下，分别比较了PSO、CS和CCS算法的收敛精度的最大值、最小值、平均值、标准误差。f1是简单的单峰函数，常用于测试算法的收敛精度，由表2的Sphere函数运行结果可知，CS算法的收敛精度远高于PSO算法，CCS算法也在一定程度上提高了收敛精度。f2～f4是复杂的多峰函数。其中： f2在搜索空间内存在多个极值点，极难优化，表2的Geiwank函数运行结果表明CS算法相比PSO算法有更好的搜索能力，CCS算法则能够更好地跳出局部最优点，搜索到更优的解； f3函数峰形呈高低跳跃，很难寻到全局最优值，常用于验算全局寻优能力和收敛能力，由表2的Rastrigin函数运行结果可知，CS算法比PSO算法具有更优的全局寻优能力，由于该函数的强烈震荡，CCS算法相比CS算法未能更好地跳出局部最优点； f4函数由于全局极小值被无限多个局部极小值所包围，很难跳出局部极小值。由表2的Rosenbrock函数运行结果可知，CS算法的收敛精度比PSO高，但CCS这种改进算法仍成功提高了收敛精度。

由图1和表3可知，PSO、CS、CCS均能够成功收敛。在达到相同目标精度的情况下，CS所需的最大迭代次数、最小迭代次数和平均迭代次数低于PSO算法，成功率高于PSO算法，而CCS算法比标准CS算法更少，成功率更高，说明混沌CS算法的收敛速度、收敛性能明显更优。综上所述，CS算法较PSO算法具有更好的寻优能力，但仍有很大的改进空间。由实验结果可知，CCS算法这种改进算法比CS算法具有更优的寻优能力。

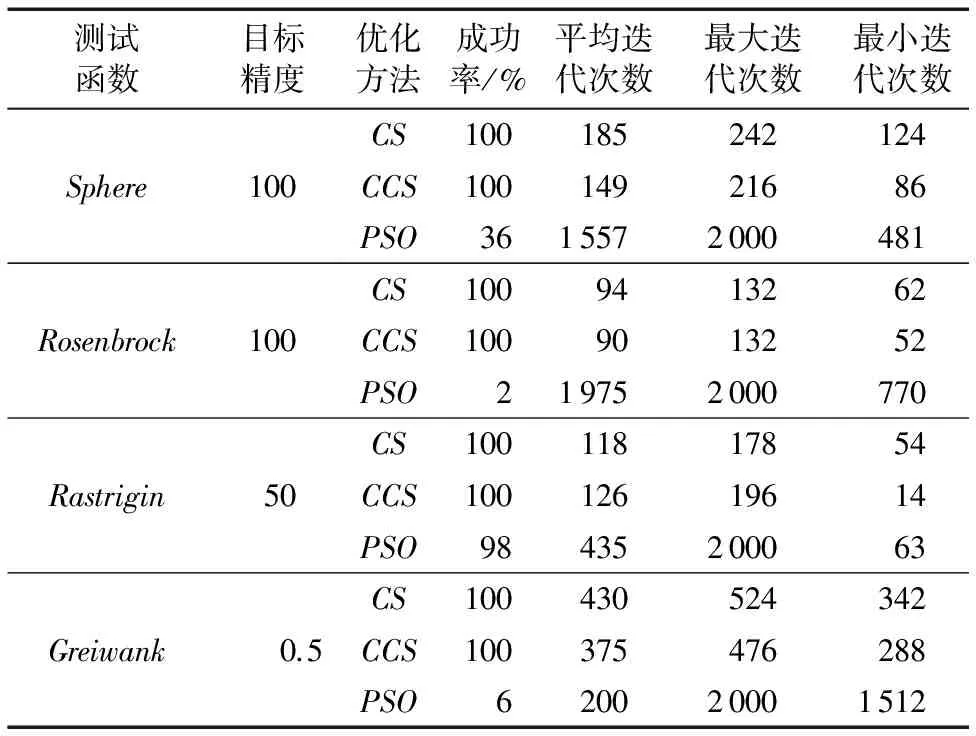
表3 4个测试函数固定目标精度下的实验结果

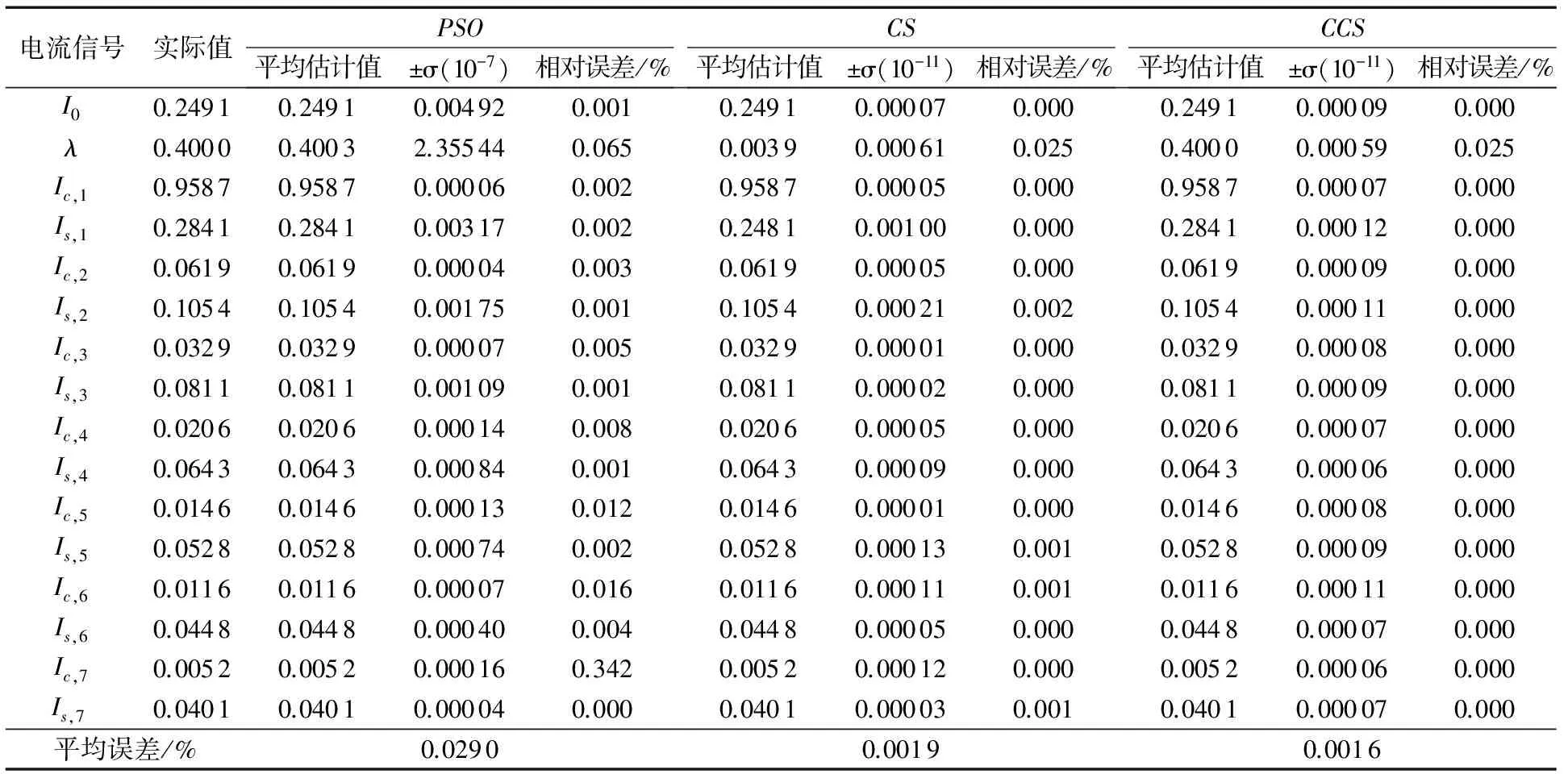
表4 CCS、CS与PSO算法谐波估计的性能比较

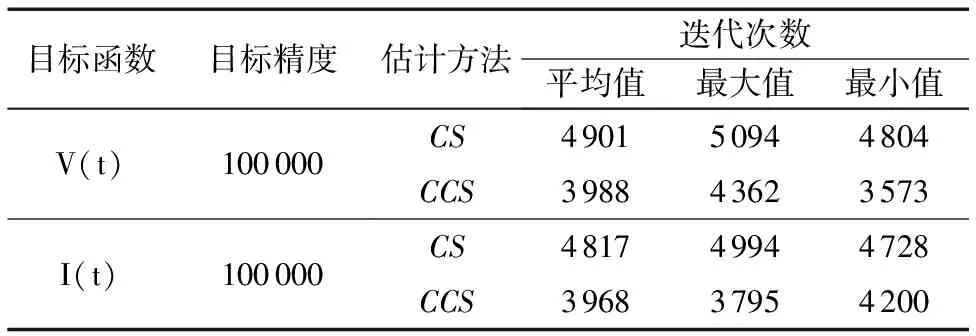
表5 固定目标精度下实验结果

4.2 谐波估计的结果

在这里采用文献[11]中的谐波电流信号，其数学表达式为：

I(t)=0.249 1e-0.4t+0.958 72 cos(ωt)+0.284 1 sin(ωt)+ 0.061 9 cos(2ωt)+0.105 4 sin(2ωt)+0.032 9 cos(3ωt)+ 0.081 1 sin(3ωt)+0.020 6 cos(4ωt)+0.064 3 sin(4ωt)+ 0.014 6 cos(5ωt)+0.052 8 sin(5ωt)+0.011 6 cos(6ωt)+ 0.044 8 sin(6ωt)+0.005 2 cos(7ωt)+0.040 1 sin(7ωt)

在文献[11]中，分别使用了离散傅里叶变换方法和PSO算法进行了谐波估计，结果显示PSO算法比离散傅里叶方法的估计精度更高，但是PSO算法谐波估计没有达到最优估计。在这里，对CS算法谐波估计与PSO算法谐波估计进行了比较。CS算法的参数设置于文献[11]相同，采样个数为64，种群规模为30，最大迭代次数为15 000，算法独立运行10次。

表4是采用PSO算法与CS算法及CCS算法分析谐波电流的实验结果。实验分别比较了估计均值和标准偏差，实验结果显示CCS算法可以更加精确地估计谐波成分，特别是对直流衰减分量的时间常数λ的估计；并且在估计电流信号时，CCS算法的标准偏差比PSO算法要小5个数量级，比CS算法小两个数量级。说明CCS算法比PSO算法及CS算法更加精确，更加稳定和可靠。由于取Δ=0.000 01，所以适应度函数EF的最大值为100 000。固定目标精度为100 000，用布谷鸟算法与混沌布谷鸟算法估计谐波成分。由表5可知混沌布谷鸟算法在达到目标精度时所需的最大迭代次数、最小迭代次数、平均迭代次数均比标准CS算法要少。这说明混沌布谷鸟算法有更快的搜索能力，具有很好的实用性和寻优的有效性。

5 结语

混沌运动具有遍历性、随机性和规律性等优点，将混沌理论引入CS算法有效提高了标准CS算法的优化性能，弥补标准CS算法后期收敛速度慢、收敛精度不高等不足。通过对4个基准函数仿真测试，实验结果证明了这种改进方法的有效性。将CCS算法应用于谐波估计后，通过仿真实验，结果表明，与基于PSO算法的谐波估计方法相比，基于CCS算法的谐波估计方法具有更高的估计精度，特别是对直流衰减分量的时间常数的估计。但是CCS算法并没有在总体变量上得到优化，如何改进算法更好地适用于谐波估计，这将是进一步的研究内容。

)

[1]YANGXS,DEBS.Engineeringoptimizationbycuckoosearch[J].InternationalJournalofMathematicalModellingandNumericalOptimization, 2010, 1(4)： 330-343.

[2] 白国振，荆鹏翔.基于改进粒子群算法的并联机械手运动学参数辨识[J].信息与控制，2015，44(5)：545-551.(BAIGZ,JINPX.Kinematicparameteridentificationofparallelmanipulatorbasedonimprovedparticleswarmalgorithm[J].InformationandControl, 2015, 44(5): 545-551.)

[3]TOLEDOCFM,OLIVEIRALD,PEREIRARDF,etal.Ageneticalgorithm/mathematicalprogrammingapproachtosolveatwo-levelsoftdrinkproductionproblem[J].Computers&OperationsResearch, 2014, 48(48): 40-52.

[4]YAHYAM,SAKAMP.Constructionsitelayoutusingmulti-objectiveartificialbeecolonyalgorithmwithLevyflights[J].AutomationinConstruction, 2014, 38(3): 14-29.

[5]RAJABIOUNR.Cuckoooptimizationalgorithm[J].AppliedSoftComputing, 2011, 11(8): 5508-5518.

[6] 刘长平，叶春明.求解置换流水车间调度问题的布谷鸟算法[J].上海理工大学学报，2013，35(1)：17-20.(LIUCP,YECM.Cuckoosearchalgorithmforsolvingpermutationflow-shopschedulingproblems[J].JournalofUniversityofShanghaiforScienceandTechnology, 2015, 35(1): 17-20.)

[7]LIXT,WANGJN,YINM.Enhancingtheperformanceofcuckoosearchalgorithmusingorthogonallearningmethod[J].NeuralComputingandApplications, 2014, 24(6):1233-1247.

[8]UROMI,FISTERIF.Hybridself-adaptivecuckoosearchforglobaloptimization[J].SwarmandEvolutionaryComputation, 2016，29(3)： 47-72.

[9] 龙文，陈乐.求解约束化工优化问题的混合布谷鸟搜索算法[J].计算机应用，2014，34(2)：523-527.(LONGW,CHENL.Hybridcuckoosearchalgorithmforsolvingconstrainedchemicalengineeringoptimizationproblems[J].JournalofComputerApplications, 2014, 34(2): 523-527.)

[10] 孙强，王雪，罗凤章，等.基于布谷鸟算法的分布式光伏并网接纳能力计算[J].电力系统及其自动化学报，2015，27(S1)：1-6.(SUNQ,WANGX,LUOFZ,etal.Capacityofdistributionnetworkonacceptanceofdistributedphotovoltaicsystembasedoncuckoossearchalgorithm[J].ProceedingsoftheCSU-EPSA, 2015，27(S1)：1-6.)

[11]LIDBERGS.Evolvingcuckoosearchfromsingle-objectivetomulti-objective[D].Skovde,Sweden:UniversityofSkovde，2011.

[12]MACEDORA,DASILVAD,COURYDV.Anewtechniquebasedongeneticalgorithmsfortrackingofpowersystemharmonics[C]//SBRN’ 02:ProceedingsoftheVIIBrazilianSymposiumonNeuralNetworks.Washington,DC:IEEEComputerSociety, 2002: 7-12.

[13]DEALRABELOR,DESLEMOSMV,BARBOSAD.Powersystemharmonicsestimationusingparticleswarmoptimization[C]//Proceedingsofthe2012IEEEWorldCongressonComputationalIntelligence.Piscataway,NJ:IEEE， 2012： 10-15.

[14]YANGXS,DEBS.CuckoosearchviaLévyflights[C]//NaBIC2009:Proceedingsofthe2009WorldCongressonNatureandBiologicallyInspiredComputing.Piscataway,NJ:IEEE, 2009: 210-214.

[15] 胥小波,郑康锋,李丹,等.新的混沌粒子群优化算法[J].通信学报,2012,33(1):24-30.(XUXB,ZHENGKF,LID,etal.Newchaos-particleswarmoptimizationalgorithm[J].JournalonCommunications, 2012, 33(1): 24-30.)

ThisworkispartiallysupportedbytheGraduateScienceandTechnologyInnovationProgramofTaiyuanUniversityofScienceandTechnology(20145019),theDoctoralResearchStart-upFundsofTaiyuanUniversityofScienceandTechnology(20142003).

NIU Haifan, born in 1991, M.S.candidate.Her research interests include electromagnetic compatibility, fault diagnosis.

SONG Weiping, born in 1960, associate professor.His research interest include modern control theory and its application.

NING Aiping, born in 1974, Ph.D., lecturer.Her research interests include intelligent information processing, speech recognition.

MA Yiyuan, born in 1991, M.S.candidate.Her research interests include electromagnetic compatibility, fault diagnosis, cloud computing.

Application of chaos cuckoo search algorithm in harmonic estimation

NIU Haifan, SONG Weiping, NING Aiping*, MA Yiyuan

(SchoolofElectronicInformationEngineering,TaiyuanUniversityofScienceandTechnology,TaiyuanShanxi030024,China)

Concerning slow convergence speed in the later stage, low calculation accuracy and easily falling into the local optimum of basic Cuckoo Search (CS) algorithm, a Cuckoo Search based on Chaos theory (CCS) algorithm was proposed.Firstly, the chaos initialization was used to increase population diversity.Secondly, the chaos disturbance operator was introduced to the local optimal value to jump out of the premature convergence and improve the calculation accuracy.Finally, the global optimization was improved.Four single objective benchmark functions were tested.The simulation results in the best, the worst, average, median and standard deviation value show that CCS algorithm has faster convergence speed and higher convergence precision than CS algorithm.Harmonic is the vital cause of the distortion of current waveform and voltage instability.The analysis of harmonics in power quality analysis is a very important part in power system.The CCS algorithm was applied to harmonic estimation.The experimental results show that the CCS algorithm has better performance compared with the Particle Swarm Optimization (PSO) according to the analysis of harmonic current in mean value and standard deviation.

Particle Swarm Optimization (PSO) algorithm; Cuckoo Search (CS) algorithm; chaos theory; function optimization; harmonic estimation

2016-08-14;

2016-09-05。

太原科技大学研究生科技创新项目(20145019)；太原科技大学博士科研启动基金资助项目(20142003)。

牛海帆(1991—)，女，山西晋中人，硕士研究生，主要研究方向：电磁兼容、故障诊断； 宋卫平(1960—)，男，山西运城人，副教授，主要研究方向：现代控制理论及应用； 宁爱平(1974—)，女，山西运城人，讲师，博士，主要研究方向：智能信息处理、语音识别； 马艺元(1991—)，女，山西太原人，硕士研究生，主要研究方向：电磁兼容、故障诊断、云计算。

1001-9081(2017)01-0239-05

10.11772/j.issn.1001-9081.2017.01.0239

TP181

A