面向危化品仓储堆垛三维几何重建的单目视觉标定算法研究*
戴 波,安海洋,3,刘学君,周泽彧,3,李雁飞
(1.北京石油化工学院 信息工程学院,北京 102617;2.北京石油化工学院 机械工程学院,北京 102617; 3.北京化工大学 信息科学与技术学院,北京 100029)
0 引言
危化品与普通货物的化学性质存在较大差异[1],在仓储方面,我国大部分危化品仓库采用堆垛码放的方式贮存,为避免堆放过密而引发安全事故,《常用危险化学品贮存通则》对堆垛的堆距、墙距、顶距、柱距和通道距等安全距离(五距)提出了严格要求。但是国内大多数仓库对堆垛五距缺乏有效的自动化监察手段[2-3],并且安监部门难以进行实时的监督管理[4]。要实现对五距的监管,查看堆垛的实时3D贮存状态最为直观。采用单目视觉技术对危化品堆垛进行精准定位和三维几何重建,可以达到监管要求。但是该技术也存在一定难点,三维重建是成像的逆过程,其求解过程是非线性的,存在多解情况,且易受噪声干扰[5]。单目视觉技术通过单个摄像头获取图像进行三维重建,相比于双目视觉和多目视觉,它避免了因图像匹配带来的技术难点,但是因单张图像缺少深度等信息而增加了重建难度[6]。而实现三维重建首要解决的是相机标定问题。
相机标定方法主要有3种:传统标定方法、自标定方法和基于主动视觉的标定方法[7]。传统标定方法典型代表有直线线性变换法(DLT)[8-9],迭代法[10],简易标定方法[11-13]等.其优点是适用任意摄像机模型,标定精度高,不足是标定过程复杂,需要高精度的标定块,在实际应用中较难实现。自标定方法最初由Faugeras和Maybank提出[14]。该方法仅依靠多幅图像对应点之间的关系直接进行标定,灵活性强,应用范围广泛,但是其最大不足是鲁棒性差[15-16],并且需要求解Kruppa方程来获得摄像机内参数[17],相对困难。一般用于精度要求不高的场合。基于传统标定法和自标定法的局限性,有人提出了基于主动视觉的摄像机标定方法[18]。典型代表为马颂德提出的三正交平移运动算法[19]。在马颂德的基础上,胡钊政[20]提出了一种三维结构恢复和直接欧式重建算法,相机仅需作一组三正交平移运动即可,降低了约束条件。
这些经典的标定算法在实现过程中均相对复杂,如需要精准标定块、标定板作参考,或者需要相机以特定的方式运动获取多幅图片进行匹配对比等。由于投影矩阵需要求解的未知参数较多,在算法实现上也存在不小的运算量。在立方体几何三维重建问题上,文献[21]通过单摄像机在2次不同焦距情况下对同一物体拍摄图像,根据2幅图像同一特征点不同的像素坐标结合当前的相机焦距等信息推算该点的世界坐标,实现了物体的几何重建,但前提需要已知精准的相机焦距参数。文献[22]利用最小二乘法实现摄像机的标定,直接通过地砖的角点做参考标定相机参数,但是结果易受相机高度和俯仰角的影响,鲁棒性较差。文献[23]将针孔模型应用在视觉测距中,通过相似三角形原理,测算目标物与相机的一维距离,无需已知相机的内参数,但是相机俯仰角对测算结果影响很大,且不易精确测量。文献[24]提出一种投射点几何转换的方法测算物体的高度,与测距原理类似,测算结果对相机角度参数要求较高,且该方法依靠被测物先验知识仅能实现一个维度的测量。文献[25]提出一种利用灭点几何原理实现规则物体的三维重建,但是仅能对平行边缘物体进行重建且需已知相机焦距参数。
在危化品仓储应用中,繁琐的相机标定过程显然不符实际应用需求,因为相机使用中可能会随时改变一些参数,并且相机往往固定在仓库角落不会移动。需要一种简单可行的方法快速确定相机参数实现视觉定位和三维重建,同时要求测算得到的相机参数有较强的鲁棒性。本文首先构建了单目视觉三维投影模型,提出了一种依托环境中标识点与其像点对应关系的相机标定方法。该方法仅需已知摄像机的三维坐标即可,无需测算相机内参数和空间角度等难以精确得到的信息,可得到投影模型的参数,简化了传统标定过程且保证了较高精度。三维几何重建过程是相机参数标定的线性逆运算,由得到的参数作为基础条件首先求取堆垛在空间的特殊解,即实现射影重建,再根据箱体几何结构属性作为约束,最终实现欧式意义下的三维几何重建。由此重建的结果客观上对标定算法的易用性和精确性进行了验证。
1 基于危化品仓库标识点的相机标定
1.1 单目视觉下相机标定问题描述
三维空间中每个成像范围内的物点信息都与其像点信息存在对应关系,这种对应关系由摄像机成像的几何模型决定。传统的成像模型一般以针孔模型作为研究,基于该模型有学者定义了4种坐标系[26]的数学转换实例化,存在如下关系[27]:
(1)

由式1可以得出结论:在矩阵M确定的情况下,由图像上像点坐标不能唯一确定其物点在世界坐标系下的实际坐标,但可以确定其三维坐标解空间,结合其他约束条件,即可确定唯一解。由此分析,实现三维几何重建的前提是确定投影矩阵M,但是矩阵M未知元素较多,需要至少6个物点与像点的对应关系才可求解,计算过程复杂。为此本文构建了单目视觉成像模型来建立世界坐标与像素坐标的线性关系,摒弃了繁琐的矩阵变换过程,大大简化了标定过程。
考虑到危化品仓库应用中的客观约束条件,首先做出以下说明:相机位置固定(光心坐标不变);实验中堆垛货物为规则长方体;标识点、线均设于地平面(z=0)上(实际环境中处于墙面、柱子等标识点、线可换算地平面上)。
1.2 单目视觉成像模型
在单目视觉测距模型的基础上,构建了五元组单目视觉成像模型:

图1 单目视觉成像模型Fig.1 Monocular vision imaging model
如图1所示,该投影模型由一个五元组参数(P,γ,θ,α,β)来表示,P为摄像机光心坐标,P′为P点在地面上的垂直投影,PO为P点在地面上成像投影,C为主光轴与地面的交点,与点P,PO组成的平面为投影模型对称面;γ为相机俯视角;θ为相机水平偏向角;2α,2β分别记为相机水平、垂直方向视野张角。D1D2D3D4为相机在地平面上可视区域;记四边形D1D2D5D6为相机成像平面。点C′为点C在像平面的像点,位于图像中心位置。
1.3 基于标识点的相机标定算法
将图1中的成像平面D1D2D5D6展开出来如图2所示:

图2 单目视觉成像平面Fig.2 Imaging plane of monocular vision


图3 单目视觉投影模型俯视图Fig.3 Top view of imaging model

(2)

(3)
同时可求得摄像机水平偏向角:
θ=φ1+θ1
(4)


图4 单目视觉投影模型侧视图Fig.4 Side view of imaging model
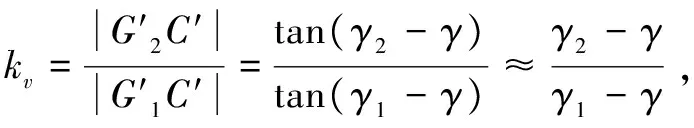
(5)
(6)
在求解相机参数α,β,γ和θ过程中,首先要已知摄像机空间坐标P(xP,yP,zP)和P点在z=0平面上的成像投影PO(x0,y0),并且两点坐标满足关系:

(7)
在实验条件中仅事先已知P=(xP,yP,zP),PO无法测得。而在求出γ和θ之前,PO=(x0,y0)无从得知。为此,首先通过循环迭代方式确定PO点位置:a.初始PO的坐标为P’的坐标,即 (x0,y0)⟸(xP,yP);b.通过投影模型计算得到摄像机参数γ和θ;c.由(7)式得到新的PO坐标,并与上一次PO坐标进行对比,若距离小于某个阈值,则认为确定PO点,否则继续进行a,b步骤。
由此,摄像机参数α,β,γ和θ均以求得,相机标定过程结束。
2 相机标定校验及货物堆垛三维几何重建
2.1 相机标定校验过程分析
将图像上的二维信息还原至空间三维信息是多解问题。故首先依据视觉投影模型求出1个特殊解,实现投影重建;再根据箱体为长方体的几何属性作约束条件求取真实解进而实现欧式空间下三维几何重建。


(8)

2.2 对单个堆垛货箱三维几何重建
在实验室环境下搭建危化品仓储模拟环境,并设立空间直角坐标系:

图5 模拟仓储环境Fig.5 Simulated storage environment

经上述迭代运算求得了点PO坐标:PO=(0.046,0.037),和各模型参数:α=24.34,β=24.42,γ=49.45,θ=39.88。根据(8)式将货物箱体角点A~G的像素坐标还原至三维空间z=0平面上,得到特殊解见表2。

表1 求取PO迭代的误差
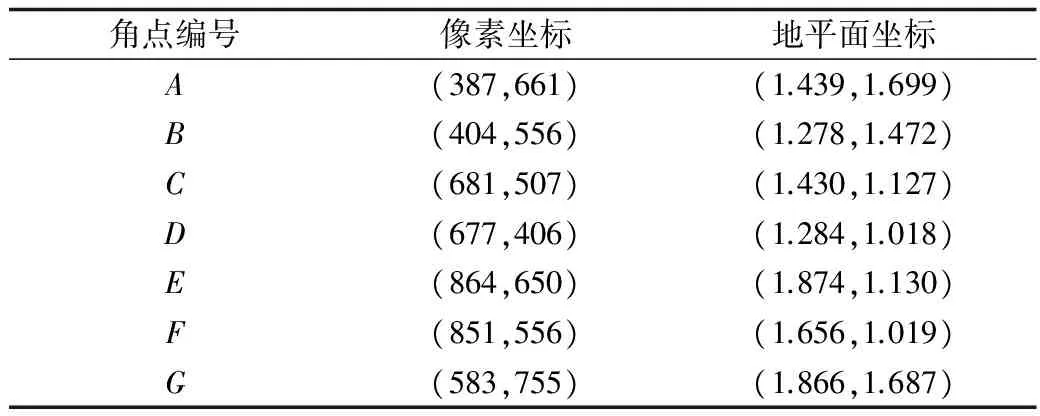
表2 特征点坐标还原情况
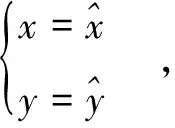
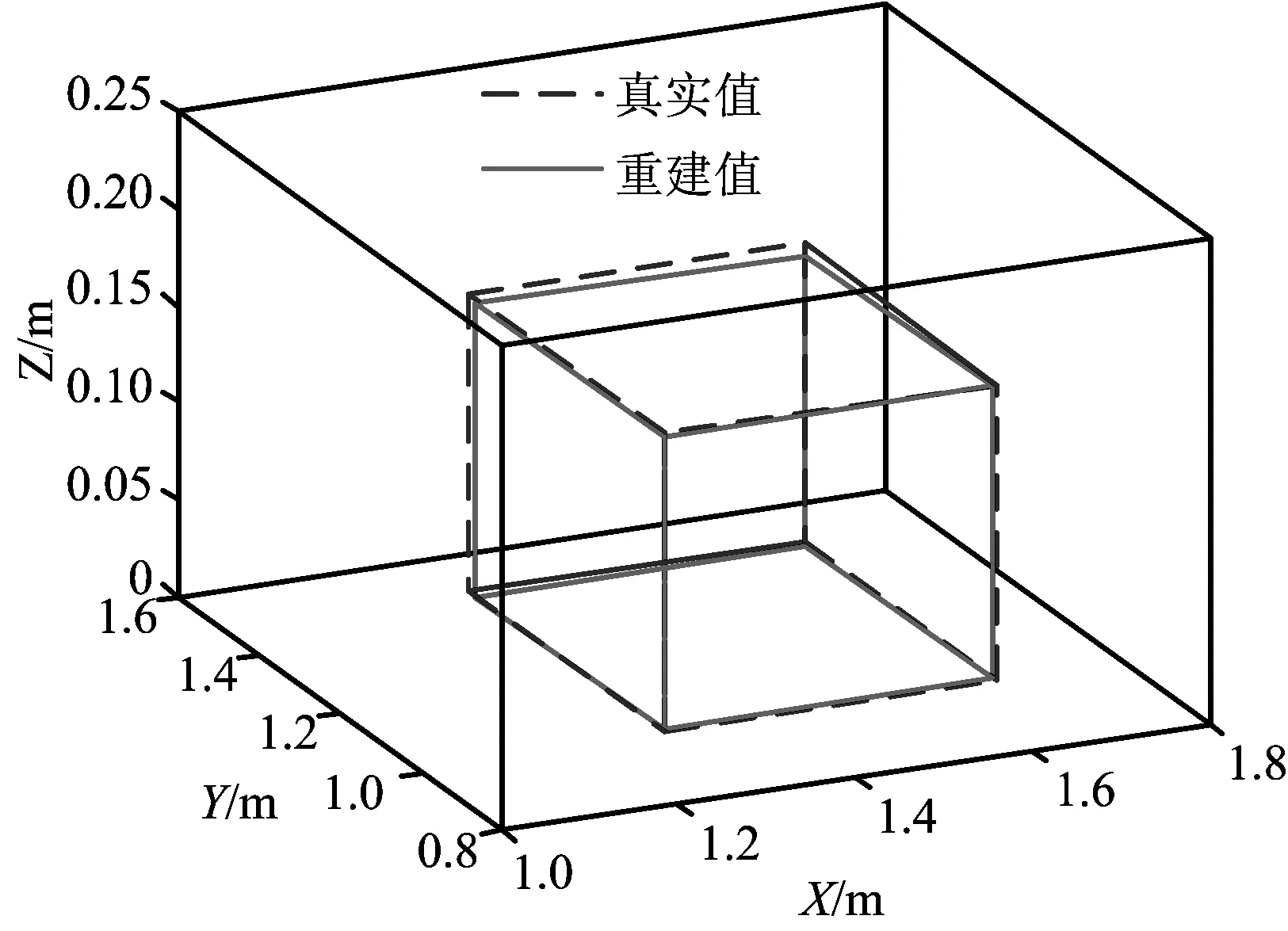
图6 单个箱体三维几何重建效果Fig.6 3D reconstruction results of single stack

图7 各顶点重建值与真实值误差Fig.7 Error of reconstruction value & actual value
(9)

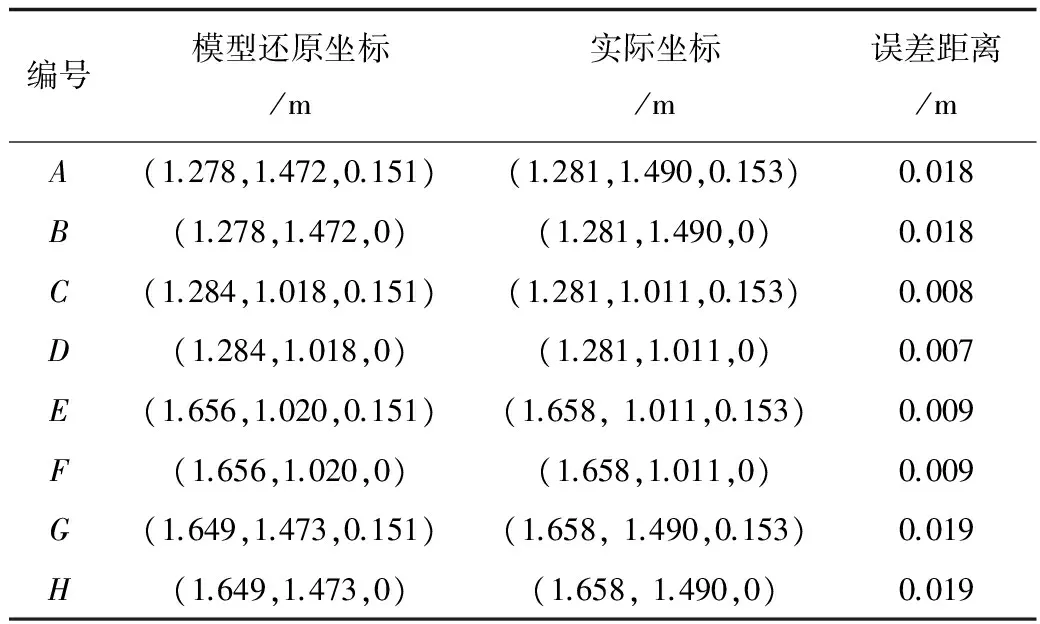
表3 三维重建结果与实际值对比
为直观对比几何重建效果,绘出三维坐标图及各顶点误差曲线,如图9、图10所示。
由图9、图10容易看出,三维几何重建后的箱体角点坐标情况基本上与实际情况重合,各顶点坐标重建值和真实值的误差距离普遍在20 mm以内,效果理想。

图8 不同时期下的堆垛状态Fig.8 Stacking state at different times

图9 多个堆垛三维几何重建效果Fig.9 3D reconstruction results of multiple stacks
2.3 对多个堆垛货箱三维几何重建
上节实现了单个货物箱体的三维几何重建,为验证标定所得相机参数能够对处于图像内各个区域的堆垛均有较精确的三维重建效果,本节通过对多个堆垛进行三维几何重建予以验证。
在存放多个货物堆垛情况下,堆垛之间存在相互遮挡情况,图像中不能获得被部分遮挡或全遮挡的货物完整角点信息,将无法实现其三维几何重建。对此,采用动态实时监测的方式,分时段三维重建。在库房空置的情况下,根据提出的算法对相机参数进行标定,然后在货物存放于仓库时,对当前完整角点信息货物堆垛进行三维重建,以此累加计算,具体实验如下:
在实验室环境下构建范围3.6 m×3.6 m×1.2 m模拟危化品仓库,首先求得点PO=(0.184 , -0.496 ),同时得到模型参数:α=23.88,β=24.99,γ=47.50,θ=55.21。图8为不同时期的堆垛情况,在每个时段对新增的当前货物堆垛进行三维几何重建。在时期1时,对1号堆垛进行三维重建,时期2时对2号堆垛三维重建,以此类推,直接给出三维几何重建结果计算结果,见表5(篇幅所限,不列出实际坐标信息)。
对比三维几何重建的效果,如图9和图10。

图10 多堆垛特征点重建值和真实值误差Fig.10 Errors of reconstruction value & actual value
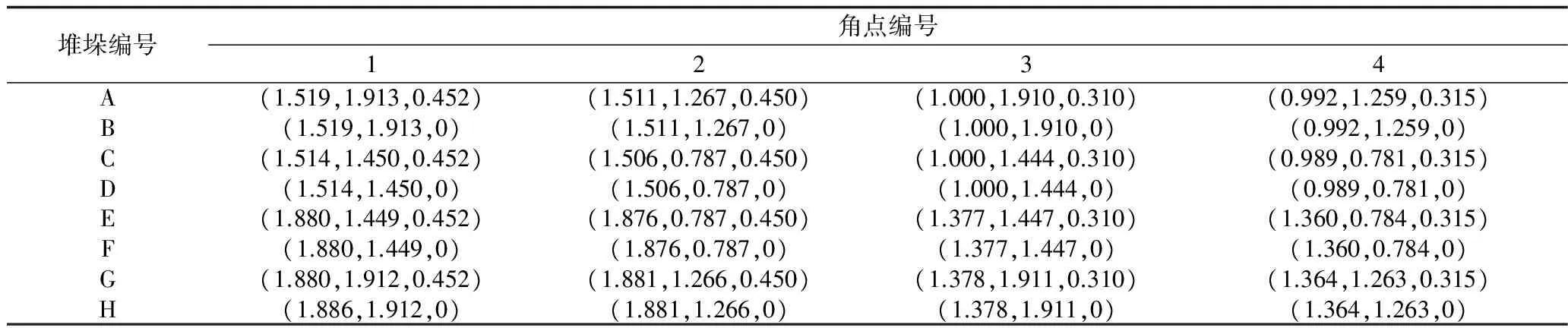
堆垛编号角点编号1234A(1.519,1.913,0.452)(1.511,1.267,0.450)(1.000,1.910,0.310)(0.992,1.259,0.315)B(1.519,1.913,0)(1.511,1.267,0)(1.000,1.910,0)(0.992,1.259,0)C(1.514,1.450,0.452)(1.506,0.787,0.450)(1.000,1.444,0.310)(0.989,0.781,0.315)D(1.514,1.450,0)(1.506,0.787,0)(1.000,1.444,0)(0.989,0.781,0)E(1.880,1.449,0.452)(1.876,0.787,0.450)(1.377,1.447,0.310)(1.360,0.784,0.315)F(1.880,1.449,0)(1.876,0.787,0)(1.377,1.447,0)(1.360,0.784,0)G(1.880,1.912,0.452)(1.881,1.266,0.450)(1.378,1.911,0.310)(1.364,1.263,0.315)H(1.886,1.912,0)(1.881,1.266,0)(1.378,1.911,0)(1.364,1.263,0)
由图9和图10可见,对多个堆垛箱体进行三维几何重建,重建效果与实际情况基本吻合,误差普遍在40 mm范围内,相对于堆垛间距和自身尺寸而言,影响基本可以忽略。由此也验证了标定得到参数对图像上不同位置的堆垛均有很好的还原效果,客观验证了标定算法的精确性。
结合实验过程,分析误差原因有以下几点:测量上的人为误差,包括摄像机光心空间坐标,堆垛箱体实际位置;摄像机自身的误差,实际成像不完全符合小孔成像模型,镜头存在畸变或光心偏离中心等;图像特征提取的误差,所得角点坐标信息受到图像噪声等干扰造成精度下降等。
3 结论
1)构建了五元组单目视觉成像模型来诠释物点与像点之间的对应关系,避免了因繁琐的坐标系变换过程而造成的标定困难问题。
2)提出一种通过识别标识点求解相机参数的方法,该方法无需已知相机内参数且标定结果具有较强的鲁棒性,同时因为仅需摄像机空间位置及2个标识点的对应关系就可实现标定,所以更易于现场实现。
3)采用特征点坐标还原的方式实现了堆垛的三维几何重建,不仅还原了堆垛尺寸信息,同时也确定了其在空间的摆放位置,实现堆垛贮存状态场景的复原。三维重建的效果也间接验证了本文标定算法的精确性。
[1]LIU J N, Chen T, FAN D L, et al. Ranking and screening hazardous chemicals for human health in southeast China[J]. Organic Chemistry Current Research, 2014, 3(126): 2161-0401.
[2]柴保身. 我国危险品仓储业发展现状与展望[J]. 物流工程与管理,2009(12):19-23.
CHAI Baoshen. Present situation and prospect of China's dangerous goods storage industry[J].Logistics Engineering and Management, 2009(12):19-23.
[3]汪涛. 探究当前危化品企业存在的安全问题和对策[J]. 科技风,2015(19):273.
WANG Tao. Study on the safety problems and countermeasures of the current hazardous chemicals enterprises[J]. Technology Wind,2015(19):273.
[4]范祥,叶春明,仝伟亮. 新形势下我国危化品仓储安全问题研究[J]. 物流科技,2016(10):148-151.
FAN Xiang, YE Chunming , TONG Weiliang. Study on the storage security of dangerous goods in China under the new situation[J]. Logistics Sci-Tech,2016(10):148-151.
[5]陈泽志. 由非定标图像序列重建和测量三维物体[D].西安:西安电子科技大学,2002.
[6]张利. 基于单目视觉和双目视觉的图像三维重建技术研究[D].兰州:兰州理工大学,2014.
[7]邱茂林,马颂德,李毅. 计算机视觉中摄像机定标综述[J]. 自动化学报,2000(1):47-59.
QIU Maolin, MA Songde, LI Yi. Overview of camera calibration for computer vision[J]. Acta Automatica Sinica,2000(1):47-59.
[8]Abdel-Aziz Y I. Direct linear transformation from comparator coordinates in close-range photogrammetry[A]// Asp Symposium on Close-Range Photogrammetry in Illinois[C]. 1971(1):1-18
[9]Faugeras O D,Toseani G. The calibration problem for stereo. In: Proc IEEE Conference on Computer Vision and Pattern Recognition, Miami Beach, Florida, 1986: 15-20
[10]Weng J Y, Cohen P, Herniou M. Camera calibration with distortion model and accuracy evaluation[J]. IEEE Trans Pattern Analysis and Machine Intelligence, 1992, 14(10): 965-980
[11]Zhang Z Y. Flexible camera calibration by viewing a plane from unknown orientations. In: Proc International Conference on Computer Vision, Kerkyra, Greece,1999: 666-673
[12]Meng X Q, Li H, Hu Z Y. A new easy camera calibration technique based on circular Points. In: Proc the 11th British Machine Vision Conference, Bristol, United Kindom, 2000: 496-505
[13]王晓华,傅卫平.一种改进的摄像机标定方法[J]. 东北林业大学学报,2007,35(6):51-53.
WANG Xiaohua, FU Weiping. A new approach for camera calibration[J]. Journal of Northeast Forestry University, 2007,35(6):51-53.
[14]Maybank Stephen J, Faugeras Olivier D. Theory of Self-calibration of a Moving Camera[J]. International Journal of Computer Vision, 1998, 8(2): 123-151.
[15]Hartley R, Hayman E, de Agapito L, et al. Camera calibration and the search for infinity[A]. In: Proc the 7th International Conference on Computer Vision[C]. Kerkyra, Greece, 1999: 510-517
[16]雷成,吴福朝,胡占义. Kruppa方程与摄像机自标定[J]. 自动化学报,2001(5):621-630.
LEI Cheng, WU Fuchao, HU Zhanyi. Kruppa equations and camera self-calibration[J]. Acta Automatica Sinica, 2001(5):621-630.
[17]张涛. 基于单目视觉的三维重建[D].西安:西安电子科技大学,2014.
[18]胡占义,吴福朝. 基于主动视觉摄像机标定方法[J]. 计算机学报,2002(11):1149-1156.
HU Zhanyi, WU Fuchao. A review on some active vision based camera calibration techniques[J]. Chinese Journal of Computers, 2002(11):1149-1156.
[19]Ma S D.A self-calibration technique for active vision system[J]. IEEE Trans Robot Automation, 1996, 12(1):114-120
[20]胡钊政,谈正. 一种基于主动视觉的三维结构恢复和直接欧氏重建算法[J]. 自动化学报,2007(5):494-499.
HU Zhaozheng, TAN Zheng. A novel algorithm for 3D structure recovery and direct euclidean reconstruction using active vision[J]. Acta Automatica Sinica, 2007(5):494-499.
[21]赵萌. 基于单摄像机的三维几何重建方法研究[D].哈尔滨:哈尔滨工业大学,2009.
[22]李然. 基于单目视觉的室内环境三维重构研究[D].长春:吉林大学,2007.
[23]鞠升辉. 基于单目视觉的移动机器人室内定位与运动目标跟踪[D].天津:天津理工大学,2016.
[24]屈姗姗,陈潇,吴晓红,等. 基于单目视觉测距的测高测面积方法[J]. 科学技术与工程,2016(2):224-228.
QU Shanshan, CHEN Xiao,WU Xiaohong,et al. A method for measuring the height and area based on distance estimation of monocular vision[J]. Science Technology and Engineering, 2016(2):224-228.
[25]冯强. 一种利用单张影像进行规则物体三维重建的方法[J]. 测绘与空间地理信息,2016(10):154-156.
FENG Qiang. 3D reconstruction based on vanishing point principle from a single image[J]. Geomatics & Spatial Information Technology, 2016(10):154-156.
[26]马颂德,张正友.计算机视觉—计算理论与算法基础[M].北京:科学出版社,1998.
[27]冯春. 基于单目视觉的目标识别与定位研究[D].南京:南京航空航天大学,2013.

