第三方挖掘作用下PE燃气管道失效行为研究*
李 军,张 宏,吴 锴,顾晓婷,夏梦莹,刘啸奔
(1. 中国石油大学(北京) 机械与储运工程学院,北京 102249; 2. 中石油昆仑燃气有限公司,北京 100101;3. 长江大学 石油工程学院,湖北 武汉 430100)
0 引言
近年来,随着城市建设的加快与燃气管道数量的急剧增加,由第三方破坏导致的燃气管道事故也逐渐增加[1]。由于第三方作用下破坏的管道主要位于公共区域,管道破坏后燃气泄漏一旦引发爆炸很容易导致次生事故[2]。为保障管道的安全运行,研究第三方破坏下管道的失效机理有着重要的实际意义。第三方破坏形式多样,典型的包括占压、车辆载荷、挖掘施工等。其中,挖掘施工导致的后果最为严重,事故比例占第三方破坏导致管道失效事故总数的半数左右[3]。挖掘作用下管道的受力复杂,管道会发生大变形,严重时可能直接发生穿透。因此,需要开展针对燃气管道在挖掘载荷作用下的力学响应分析,找到管道失效根本原因。
不少学者开展了埋地管道在第三方载荷作用下的失效分析。澳大利亚Brooker D C等[4-5]对斗齿荷载作用下X65管道的响应行为进行了系统的分析,给出了管道失效时斗齿载荷与管道尺寸、斗齿类型之间的定量关系;姚安林[6]综合使用数值模拟与试验验证的方法,较为全面的讨论了动力作用在机械挖掘作用于管道上的影响;杨建功[7]使用位移加载形式分析了挖掘机斗齿作用深度对X65管道的影响,分析了不同加载角度下管道的变形行为,分析中没有考虑土壤的影响。这些研究主要针对机械挖掘对管道的影响,对于第三方作用下管道的失效行为也有大量研究。Zhang J[8-9]分析了坠落石块作用下埋地管道在岩石场地土条件下的力学行为,讨论了管道内的最大Mises等效应力、最大塑性应变、椭圆度等力学指标随管道尺寸和土壤条件的变化关系;Zhang L等[10]分析了第三方爆破施工对埋设管道安全性的影响,讨论了不同TNT当量条件下管道的最大应力,应变及变形程度;GuoYanbao等[11]使用ANSYS Workbench 耦合分析模块分析了管道爆炸对平行敷设管道安全性的影响;Luo等[12-13]进行了土壤沉陷和滑坡作用下聚乙烯管道的力学行为研究,其使用实体土单元模拟土壤与管道,分析了管道内最大Mises应力的变化规律;李明阳等[14]进行了PE燃气管道的力学性能测试与本构分析,讨论了交通荷载对管道性能的影响。
虽然有相关方面的研究,但针对PE管道的研究较少,且多数研究中没有考虑管土相互作用,这使得模拟工况与实际工况存在一定差异。因此,建立了考虑管土相互作用的第三方挖掘作用下PE燃气管道响应的非线性有限元模型,模型使用实体单元模拟土壤,使用壳单元模拟管道,面面接触算法模拟管土作用。基于该模型,进行了典型工况的管道的失效过程分析,使用基于应力与基于应变准则对管道的安全性进行了评价。开展了工程常见参数的影响分析,讨论了挖掘位置、管径、壁厚以及工作内压对管道结构的影响。
1 PE管道的主要失效形式与准则
埋地管道的典型失效形式包括强度失效、屈曲失效和过量变形。在机械齿作用下管道主要在局部产生巨大的应力与变形,主要的失效形式体现为强度失效和过量变形失效。
现有的工程中,针对聚乙烯管道的强度失效准则主要包括基于应力的失效判定准则和基于应变的判定准则2种。
1.1 基于应力的失效准则
在基于应力的判定准则中,主要使用屈服强度作为判定指标,需要保证管材在载荷作用下的最大Mises等效应力小于屈服强度。Von Mises屈服条件为最大形状改变比能达到一定值时发生屈服,屈服条件的表达式为:
(1)
式中:σ1,σ2,σ3分别为第一、二、三主应力。
1.2 基于应变的失效准则[15]
基于应变的管道强度设计方法的数学表达式与基于应力的方法相类似:
(2)
式中:ε为各种载荷作用时管道可能产生的最大应变;εs为管材所能承受的极限应变,一般通过对管材的试验测试获得;F为设计系数;[ε]为许用应变。
由于PE管材的拉伸性能较好,一般其极限拉应变达到30%,但是由于材料处于大变形状态下时其稳定性能很差,所以埋地管道抗震设计规范[16]中建议当最大拉应变达到20%时,可以认为管道材料达到了极限状态。
管道的压缩极限应变应根据有效的分析方法或物理测试,或二者同时采用。在缺乏更多详细信息的情况下,埋地管道抗震设计规范[16]推荐PE管道压缩极限应变可按下列式计算:
(3)
式中:[εc]为管段的压缩许用应变;t为管道壁厚,m;D为管道外直径,m。
工程中针对PE管道的过量变形主要使用椭圆度判定,CSAZ662[17]给出了椭圆度的标准计算公式:
(4)
式中:Δ为管道椭圆度;Dmax为管道外径最大值,mm;Dmin为管道外径最小值,mm。
由于椭圆度主要影响管道的通径,所以在长输管道中对其有严格的要求,针对PE管道尚没有明确的椭圆度临界要求,但不可否认其为管道的1个重要变形指标,所以在参数分析中也考察其变化规律。
2 挖掘作用下城市燃气管道力学响应数值分析
2.1 管材模型
PE管道的管材采用拉伸得到的工程应力应变数据描述,其曲线呈现为类似于幂次函数的形状,在弹性段,模量近似为663.4 MPa,泊松比为0.45。在超过屈服强度21 MPa后,管材承载能力明显降低,但由于PE材料塑性较好,其仍保持着一定的承载能力,直到材料拉断[12-13]。
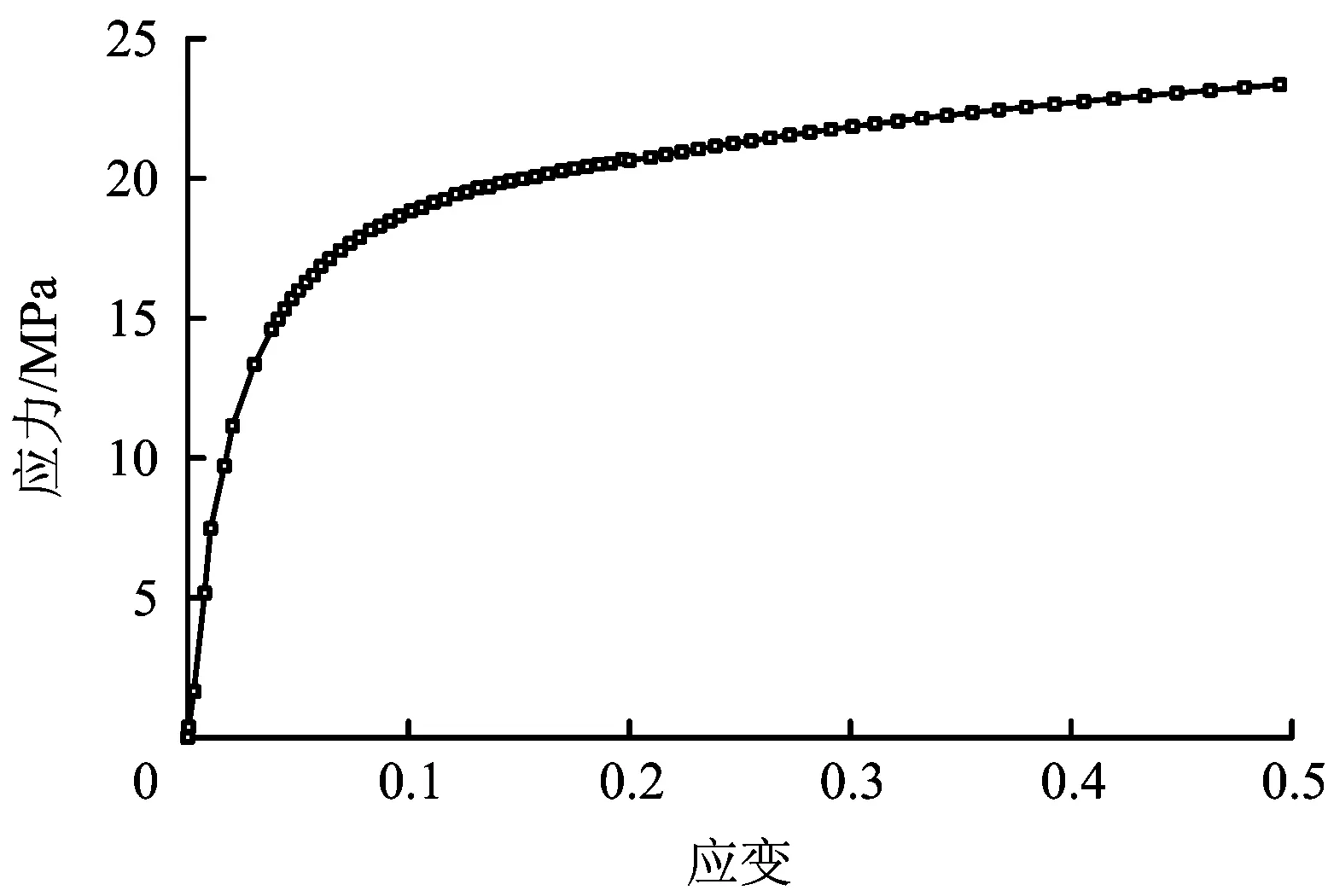
图1 PE材料应力应变曲线Fig.1 Engineering Stress-strain curve of the PE material
2.2 土壤模型
土壤采用摩尔库伦模型描述,典型参数如表1所示,由于摩尔库伦模型必须包含凝聚力,对于砂土该值通常取1个较小值,以下取4 kPa。

表1 土壤摩尔库伦模型参数
2.3 有限元模型
挖掘机载荷主要来自于液压载荷,市政工程中,常见挖掘机能提供10 kN的挖掘力。在挖掘力的作用下挖斗端部机械齿会直接对管道产生巨大的挤压作用最终引发管道失效。
采用通用非线性有限元分析软件ABAQUS建立挖掘作用下燃气PE管道力学响应分析模型。管道总长取3 000 mm,管径壁厚按照实际工程参数选取,土块长度与管道一致,高度和宽度均为600 mm。挖掘机械齿采用工程中常见的锥型挖掘机齿,尺寸如图2所示。

图2 挖掘机斗齿形状示意Fig.2 Sketch of the tooth of excavator

图3 机械齿挖掘作用下管道响应有限元模型Fig.3 Finite element model for pipeline under excavator load
有限元模型中,土壤与管道使用六面体减缩积分单元C3D8R模拟,管道径向划分为4层单元,管道环向上半部分划分为64个单元,下半部分划分为16个单元。对土壤XY平面约束Z方向平动,XZ平面约束Y方向平动,底面约束X方向平动,将管道两端全约束。采用面-面非线性接触算法定义管道和斗齿以及管道与土壤间的接触。与机械齿接触部分管道轴向划分较密,两端接触区相距较远部分轴向划分较稀疏。由于机械齿刚度远大于PE管道,将其约束为刚体,在计算中忽略其变形作用来加快模型的收敛性。整体有限元模型如图3所示。
3 典型工况PE管道失效历程分析
以某1典型工况为例,分析PE管道在机械齿作用下的力学响应行为。管道直径为110 mm,壁厚10 mm,管道压力0.4 MPa。土壤参数取2.2节中提供的土壤特性参数。挖斗机械齿垂直作用于管道,共施加10 000 N的挖掘力,分析加载过程中管道的应力应变状态。图4给出了机械齿作用下管道内最大Mises应力和最大应变随加载力的变化关系。图5、图6分别给出了不同机械齿作用下管道的Mises应力分布和截面椭圆度,可以看到,随着加载力的增加,应力和应变均增大,但应力的增幅越来越小,而应变增幅越来越大。这主要是由于材料进入塑性后,其承载能力降低,导致载荷增大的过程中结构内应力并不会有明显的增大,但此时材料塑性变形很大,虽然应力增加很小,应变却快速增加。

图4 管道最大Mises应力与最大应变随机械齿载荷变化Fig.4 Relationship of the Max Mises Stress and Max strain with the applied excavator load
若使用基于应力的失效准则,可以得到,当加载力达到4 500 N时,管道内最大Mises应力达到PE管材屈服强度。若使用基于应变的失效准则,加载力需要达到5 000 N,管道内的最大应变才会达到许用应变20%。因此,使用屈服强度的准则对于PE管道来说较为保守。
数值分析过程中约束土壤侧面、底面与管道端面的法线方向位移。通过2个载荷步分析机械齿作用下管道的响应过程。第1个载荷步为内压载荷步,载荷步中对管道内壁施加工作压力;第2个载荷步为机械齿加载载荷步,通过对机械齿加载垂向向下的液压作用力分析管道的力学响应。

图5 不同机械齿载荷作用下管道的Mises应力分布与变形Fig.5 Mises Stress contour and deformation of PE pipe under different excacator load

图6 不同机械齿载荷作用下管道截面椭圆度Fig.6 Flattening of PE pipe under different excavator load
4 机械挖掘作用下PE管道力学响应影响因素分析
为了更加准确的得到在机械挖掘载荷作用下PE管道的力学响应行为,以下对工程中可能影响管道响应的常见影响因素进行分析。
4.1 挖掘位置的影响
由于挖掘的随机性,机械齿作用于管道的位置存在不确定性。本文考虑机械齿作用于管道不同位置时管道的响应。挖掘位置通过挖掘齿中性轴距管道中心轴距离δ来确定,具体关系如图7所示。

图7 机械齿作用位置示意Fig.7 Sketck for the contact position for the tooth and pipe
首先分析挖掘位置不同时管道内的最大Mises应力分布。图8给出了10 000 N载荷作用下,δ从0~30 mm变化过程中,管道的整体变形和Mises等效应力的分布云图。可以得到管道的最大应力位置均处于机械齿与管道接触面的端部,4种状态下管道最大Mises应力大小并没有明显的区别。这主要是在10 000 N挖掘力作用下管道已经进入了大变形状态,管道承载力较小。

图8 不同挖掘位置管道的Mises应力分布与变形Fig.8 Mises Stress contour and deformation of PE pipe at different positions
虽然最大Mises应力变化不大,但是随着挖掘偏移距离的增加,同样挖掘力下管道截面椭圆度发生了一定的下降。在δ从0 mm增加到3 mm的过程中,管道截面椭圆度下降了10%,如图9所示。

图9 不同挖掘距离管道截面椭圆度Fig.9 Flattening of PE pipe under different excavator positions

图10 不同挖掘位置危险管截面环向等效应力分布Fig.10 Mises stress distribution in the critical pipe section for different excavator positions
为了更加详细的分析管道内应力的分布,图10给出了管道危险截面环向Mises等效应力的分布情况,当δ=0 mm时,管道最大Mises应力出现在管道顶部,管道最小Mises应力出现在管道底部。管道截面内等效应力关于竖直中轴线对称。同时在距离管道端部60°左右位置管道应力较大,在0°~60°的过程中管道应力先减小后增大。分析可以得到机械齿作用下管道在环向顶部和距离顶部60°左右位置弯曲变形最大,从而导致其等效应力最大。随着δ的增加,机械齿作用位置开始偏移,这时管道内最大Mises应力位置也跟着发生了偏移,同时整个管道截面上的等效应力分布形式也发生了类似的旋转。
图11给出了管道危险截面环向最大应变的分布情况,从分布规律上来说最大应变分布规律与最大应力较为类似。但可以得到的是,在δ=10 mm时,管道内的最大应变最大,达到0.166。但总体来说,挖掘位置的影响较小。
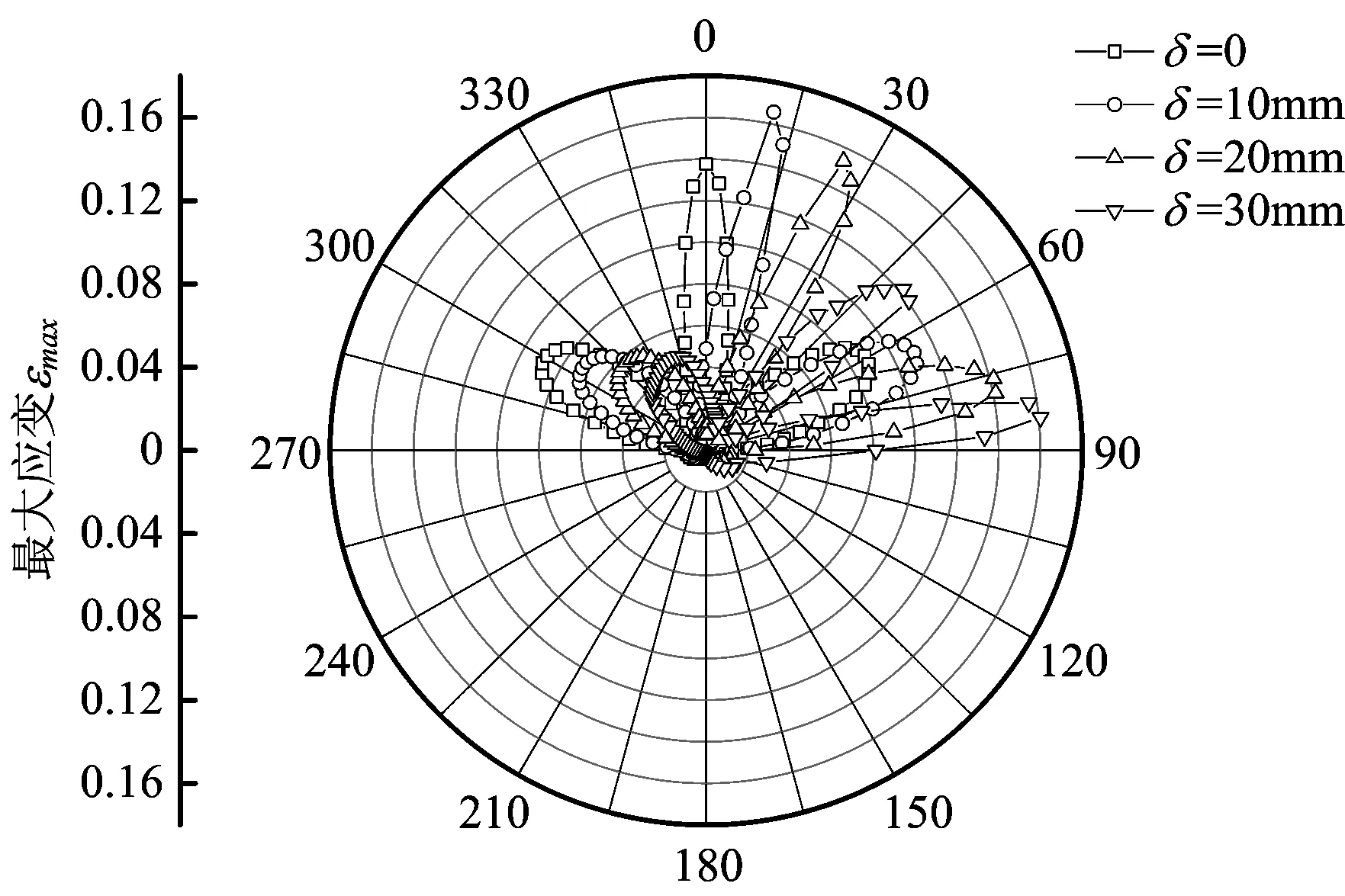
图11 不同挖掘位置危险管截面环向最大应变分布Fig.11 Mises stress distribution in the critical pipe section for different excavator positions
4.2 管径的影响
PE管道在城市中担任多种输送任务,从而城市内分布着众多管径不一的管道,选取从75~225 mm共5种常见尺寸的PE管道进行分析,挖掘位置取管道端部无偏移位置。图12给出了不同管径PE管道在10 000 N挖掘力下的整体变形云图和Mises等效应力分布云图。可以发现,随着管径的增加管道整体变形明显变小,同时管道最内最大应力也出现了降低。

图12 不同管径下管道的Mises应力分布与变形Fig.12 Mises Stress contour and deformation of PE pipe for different pipe diameters
图13给出了管道内最大Mises应力与椭圆度随管径的变化关系。由图可见,管道内最大应力基本保持不变,但椭圆度发生了骤降,由75 mm管径时的0.9下降到了225 mm时的0.21。

图13 管道截面椭圆度与最大Mises应力随管径变化关系Fig.13 Relatioship of the flattening parameter and Max Mises stress with the pipe diameter
同样为了更加准确的分析管道内的应力状态,对整个管道截面内的应力环向分布进行详细的讨论。从图14可以得到,在所有情况下管道内的最大Mises应力均出现在管道的顶部,即机械齿与管道的接触位置,最小位置均出现在管道的底部。同时随着管径的增加管道底部应力逐渐减小。这主要是当管径较小时,管道径厚比较小,在管道顶部抵抗局部变形的能力较大。随着径厚比的增大,管道刚度减小,管道的变形更加均匀,从而导致管道顶部应力的减小。
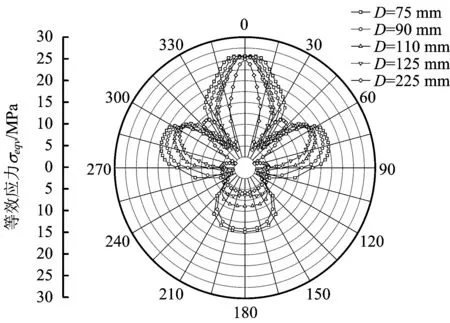
图14 不同管径下危险管截面环向等效应力分布Fig.14 Mises stress distribution in the critical pipe section for different pipe diameters
图15给出了管道最大应变分布规律,明显可以发现,其与最大应力存在着较大的差异。随着管径的增大,管道的底部应力出现了较大的增加,但应变却几乎没有发生较大的改变。这主要是由于管径增大后,管道底部的应力虽有增加但仍然处于弹性状态,使得管道的应变大小较小,从而应变的增量也较小。而与此相反的是,虽然管道顶部的应力数值上没有较大的降低,但应变却发生了较大的降低,这主要是因为管道顶部在机械齿的加载下达到了塑性状态,此时由于该部分管材过了屈服。结构应力并不会有太大的变化,但材料却进入了塑性大变形状态,应变容易产生突变。
4.3 壁厚的影响
壁厚也是PE管道最为常见的变化几何参数,壁厚的增加能够增加管道的承压能力,同时改变管道的整体刚度。本节以110 mm管径管道为例,讨论6.3~10 mm共5种壁厚条件下管道受10 000 N机械齿加载力的力学响应。图16给出了不同壁厚下管道的整体变形与Mises等效应力分布云图。可以得到随着壁厚的增加管道的变形开始减小,同时Mises等效应力也有一定的降低。图17给出了管道内最大Mises等效应力与椭圆度随壁厚的变化关系。可以看到,当管径由6.3 mm增加至9.1 mm时,管道内应力有微小的降低,但椭圆度有明显的下降。而当壁厚增加到10 mm时,管道内最大Mises应力也出现了明显的下降。这主要是壁厚的增加使得管道刚度增加,抵抗机械齿加载能力增强而导致的。

图16 不同壁厚下管道的Mises应力分布与变形Fig.16 Mises Stress contour and deformation of PE pipe for differnent pipe wall thickness

图17 管道截面椭圆度与最大Mises应力随壁厚变化关系Fig.17 Relationship of the flattening parameter and Max Mises stress with the pipe wall thickness
图18与图19分别给出了不同壁厚参数下管道截面的最大等效应力和最大应变的环向分布。由图可见,随着壁厚的变化,应力应变的分布形式并没有发生明显的变化,只是随着壁厚的增加,两者均有一定的减小。同时可以得到在壁厚增加的过程中,管道底部的应力应变没有明显的变化,均较小。

图18 不同壁厚下危险管截面环向等效应力分布Fig.18 Mises stress distribution in the critical pipe section for different pipe wall thickness
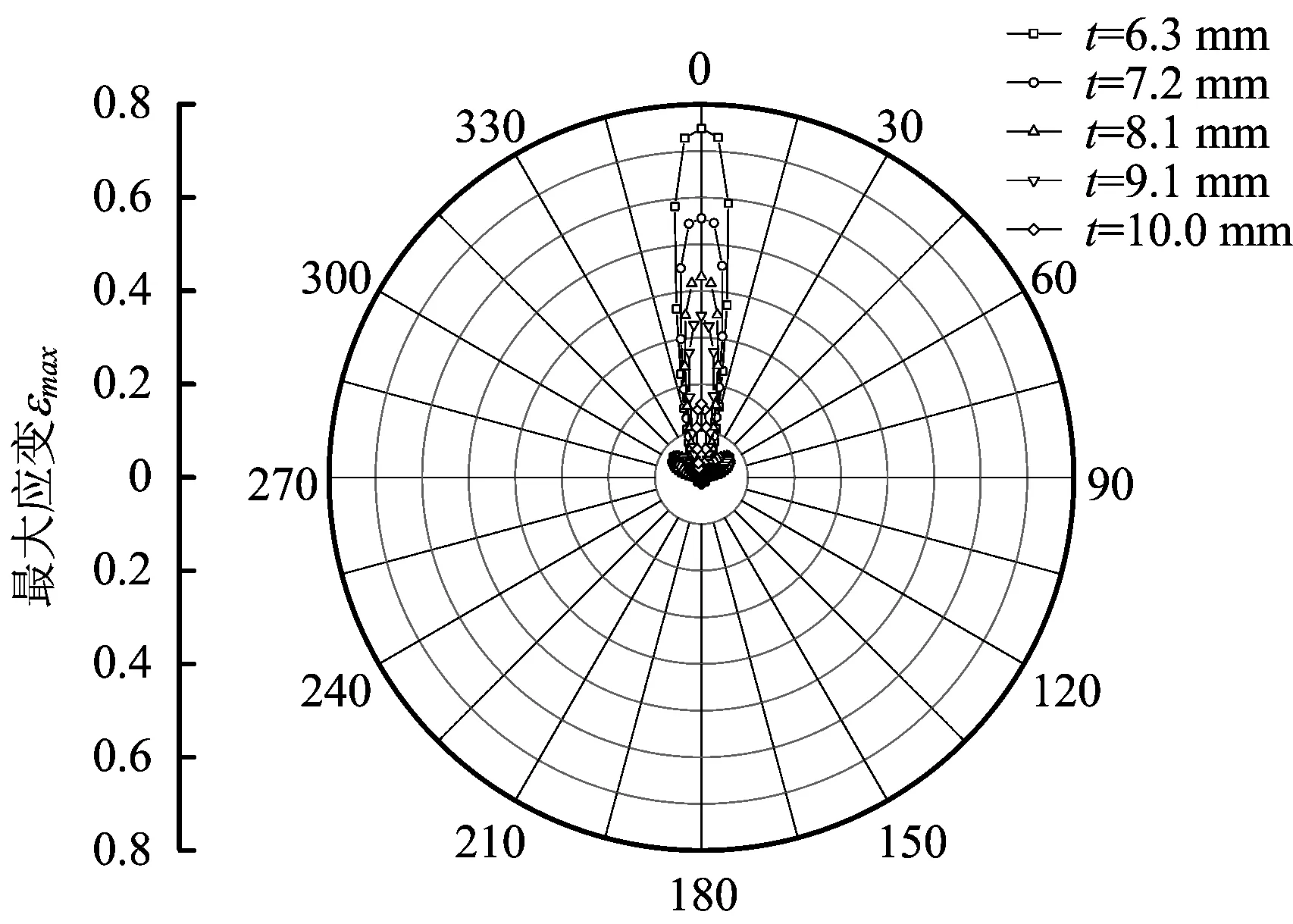
图19 不同壁厚下危险管截面环向最大应变分布Fig.19 Mises stress distribution in the critical pipe section for different pipe wall thickness
4.4 工作内压的影响
承担燃气输送的PE管道会受到工作内压的作用,按地区和工作要求不同,内压会有一定的区别,较大的内压会达到1 MPa。从而这里对不同内压下管道在机械齿作用下的响应进行分析,内压分别取0.2,0.4,0.6,0.8,1.0 MPa等5种不同结果。图20给出了不同内压情况下管道的整体变形和Mises应力分布云图,由图可见,管道内应力最大位置没有明显区别,且应力值也没有明显差异,但内压增大后,管道变形减小。图21给出了管道内最大Mises应力与椭圆度随内压的定量关系图。

图20 不同内压下管道的Mises应力分布与变形Fig.20 Mises Stress contour and deformation of PE pipe for differnent pipe internal pressures

图21 管道截面椭圆度与最大Mises应力随内压变化关系Fig.21 Realtioship of the flattening parameter and Max Mises stress with the pipe internal pressures
图22与图23分别给出了不同内压参数下管道截面的最大等效应力和最大应变的环向分布。由图可见,随着内压的增加,应力应变的分布形式整体没有发生大的变化,只是管道底部的应力逐渐增大。这主要是因为管道内压的增加使得管道的整体刚度有了一定的增加,从而使得管道对底部土壤的作用力增大,最终导致管道底部应力变大,但是由于这些应力值都很小,所以在图23中看不出管道底部应变的明显区别。

图22 不同内压下危险管截面环向等效应力分布Fig.22 Mises stress distribution in the critical pipe section for different pipe internal pressures

图23 不同内压下危险管截面环向最大应变分布Fig.23 Mises stress distribution in the critical pipe section for different pipe internal pressures
5 结论
1)机械齿作用下管道部分进入高度塑性状态,此时管道内应力状态影响因素众多且复杂。采用考虑管土相互作用的非线性有限元模型能够较好的模拟整个过程,可以在工程实际中进行定量评价时使用。
2)对于PE管材,采用基于Mises应力的失效准则与采用基于应变的失效准则时管道能够承载的最大机械齿挖掘力相差不大,采用基于Mises应力准则会更保守一点。介于PE管材性能较好,管道达到屈服强度时其实并不是极限的状态。这种情况下使用应变失效判据进行失效判定比较合理。
3)机械齿作用下管道主要失效位置为机械齿与管道接触位置两端,在机械齿作用过程中,接触位置会出现很大的应力应变,同时管道会发生很大的截面变形。
4)机械齿作用位置对管道响应影响较小。但管径和壁厚的增大能在一定程度上减小管道内的应力,同时能够很大的减小管道的截面椭圆度。内压的改变对管道内最大应力几乎没有影响,同时对椭圆度的影响也小于其他参数。
[1]李军, 张宏. 城镇燃气管道第三方破坏因素的模糊概率分析[J]. 天然气与石油, 2016, 34(2):109-114.
LI Jun, ZHANGHong. Fuzzy probability analysis on the third party damage factor for urban gas pipeline[J]. Natural Gas and Oil, 2016, 34(2):109-114.
[2]Li J, Zhang H, Han Y S, et al. Study on failure of third-party damage for urban gas pipeline based on fuzzy comprehensive evaluation.[J]. PLoS ONE, 2016, 11(11):e0166472.
[3]李军, 张宏, 梁海滨,等. 基于模糊综合评价的燃气管道第三方破坏失效研究[J]. 中国安全生产科学技术, 2016, 12(8):140-145.
LI Jun, ZHANG Hong, LIANG Haibin, et al. Study on failure of gas pipeline due to third party damage based on fuzzy comprehensive evaluation[J]. Journal of Safety Science and Technology, 2016, 12(8):140-145.
[4]Brooker D C. Experimental puncture loads for external interference of pipelines by excavator equipment[J]. International Journal of Pressure Vessels & Piping, 2005, 82(11):825-832.
[5]Brooker D C. Numerical modelling of pipeline puncture under excavator loading. Part I. Development and validation of a finite element material failure model for puncture simulation[J]. International Journal of Pressure Vessels & Piping, 2003, 80(10):727-735.
[6]姚安林, 徐涛龙, 李星,等. 基于试验和数值模拟确定挖掘机具作用下埋地输气管道的动载荷[J]. 振动与冲击, 2014, 33(17):39-46.
YAO AnLin, XU Taolong, LI Xing, et al. Determining dynamic load on a buried gas pipeline under mining machinery actions based on test and numerical simulation[J]. Journal of Vibration and Shock, 2014, 33(17):39-46.
[7]杨建功, 练章华, 于浩,等. 油气长输管道第三方破坏监测优化仿真研究[J]. 计算机仿真, 2016, 33(2):469-474.
YANG Jiangong,LIAN ZhangHua, YU Hao, et al. Simulation of third-party damages to long-distance oil and gas pipelines and study on damage monitoring and optimal[J]. Computer Simulation, 2016, 32(2): 469-474.
[8]Zhang J, Liang Z, Han C, et al. Buckling behaviour analysis of a buried steel pipeline in rock stratum impacted by a rockfall[J]. Engineering Failure Analysis, 2015, 58:281-294.
[9]Zhang J, Liang Z, Feng D, et al. Response of the buried steel pipeline caused by perilous rock impact: Parametric study[J]. Journal of Loss Prevention in the Process Industries, 2016, 43:385-396.
[10]Zhang L, Liang Z, Zhang J. Mechanical response of a buried pipeline to explosion loading[J]. Journal of Failure Analysis and Prevention, 2016, 16(4):1-7.
[11]Guo Y, He L, Wang D, et al. Numerical investigation of surface conduit parallel gas pipeline explosive based on the TNT equivalent weight method[J]. Journal of Loss Prevention in the Process Industries, 2016, 44:360-368.
[12]Luo X, Lu S, Shi J, et al. Numerical simulation of strength failure of buried polyethylene pipe under foundation settlement[J]. Engineering Failure Analysis, 2015, 48:144-152.
[13]Luo X, Ma J, Zheng J, et al. Finite Element Analysis of Buried Polyethylene Pipe Subjected to Seismic Landslide[J]. Journal of Pressure Vessel Technology, 2014, 136(3):031801.
[14]李明阳, 陈国华. 含表面裂纹PE管道临界失稳压力的计算与分析[J]. 塑料工业, 2009, 37(5):38-41.
LI Mingyang, CHEN Guohua. Calculation and analysis of the critical buckling pressure of PE pipes with surface crack[J]. China Plastic Industry, 2009, 37(5):38-41.
[15]张宏, 崔红升. 基于应变的管道强度设计方法的适用性[J]. 油气储运, 2012, 31(12):952-954.
ZHANG Hong, CUI Hongsheng. The applicability of strain-based pipeline strength design method[J]. Oil and Gas Storage and Transportation, 2012, 31(12): 952-954.
[16]SURESH R D, SUHDHIR K J. Guidelines for seismic design of buried pipeline, IITK-GSDMA-EQ33- V2.0 [S]. Kanpur, India: Authority Gujarat State Disaster Management, 2002.
[17]Canadian Standard Association, Oil and gas pipeline systems, CSA standard Z662-2011 [S]. Mississauga, Ontario, Canada: Canadian Standard Association, 2011.

