T型结构压力管道流固耦合模拟与试验验证*
王 武,陈 涛,杨 帅,吴大转,于思琦
(1.浙江大学 能源工程学院,浙江 杭州 310027;2. 杭州市特种设备检测研究院,浙江 杭州 310051)
0 引言
压力管道是公认的运输易燃易爆、有毒化工物质相对较为安全、经济的运输方式[1-2],广泛应用于石油、天然气、船舶、航空航天、生活供水等领域,尤其是在油气输送领域具有独特的优势,世界上近100%的天然气、85%的原油都是采用压力管道输送的。压力管道长期遭受流体冲刷、电化学腐蚀、疲劳破坏、外部介质等因素的作用,极易发生机械裂纹和腐蚀穿孔,导致管道输送效率降低,严重时甚至引发火灾、爆炸等安全事故,不仅会造成巨大的经济损失,还会威胁人们的生命安全、破坏生态环境[3-7]。
近年来压力管道安全事故频繁发生,造成很大的损失,其中管道振动造成的管道失效占很大比例。然而,现有文献关于内部流体激励引起的管道振动的研究,主要集中在直管[8-10]、弯管[11-13]以及U型管[14-15]。文献[8]运用ADINA对不同约束条件下阀门开关的过渡过程进行了研究;文献[9-10]推导了不同支撑条件下输液直管流固耦合振动方程的解析解;文献[11]基于流固耦合理论对1/4圆弧管道进行了研究;文献[12-13]基于ANASYS对弯曲输液管道系统的流固耦合振动特性进行了研究;文献[14-15]研究了不同内流作用下U型管的响应特性,发现管道的位移和应力随流体速度或充液加速度的增大而增大。同时,很多流体输送系统中普遍存在T型管结构,这类结构也是可能诱发管路振动的因素;文献[16]研究了斜T型管在灌装过程中的应力、应变以及内部流体的流动特性。然而,T型管内部流动相对复杂,在输送气体的条件下存在明显的流固耦合作用,对其振动特性有着显著影响。
本文利用ADINA软件对一种典型的压力管道结构—T型管的内部流体介质的非定常引起的振动特性进行了流固耦合模拟,同时利用管道系统试验系统对T型管的振动特性进行实验研究,并验证流固耦合数值方法的准确性。
1 流固耦合数学模型
管道系统流固耦合计算时,流体和结构的耦合界面必须满足2个基本条件,即位移协调方程:
df=ds
(1)
力平衡方程:
n·τf=n·τs
(2)
在流固耦合界面上,流体作用于管道内壁的力为分布力,分布力无法施加到结构节点上,需将其积分为集中力施加到结构节点上,积分公式为:
(3)
式中:df为流体位移,m;ds为结构位移,m;t为时间,s;dS为耦合界面;τf为流体应力,Pa;τs为结构应力,Pa;sd为结构节点位移,m。
在流固耦合计算中,流体模型和结构模型分开建立,它们的单元和网格可以完全不相同,只要满足时间积分是相同的即可。流体模型和结构模型的位移、速度、加速度在耦合界面上是相同的,处理时不加以区分。
流体方程和结构方程分别表示为:
Gf(f,f′)=0
(4)
Gs(d,d′,d″)=0
(5)
流体的速度和加速度用未知变量表示为:
(6)
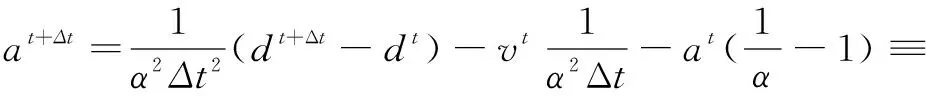
(7)
把上述各方程应用到耦合系统,得到时间积分的最终表达式为:
(8)
(9)
2 流固耦合分析
2.1 计算模型与边界条件
本文研究的对象为管道系统中常见的T型管,其几何模型与网格如图1所示,管道外径D=0.035 m,壁厚d=0.001 5 m,管长L=1.1 m。管道材料为304不锈钢,弹性模量E=1.67×1011Pa,密度ρs=7 800 kg·m-3,泊松比υ=0.3。管内流体密度ρf=1.293 kg·m-3,黏度μ=1.81×10-5Pa·s,温度K=293.15 K。

图1 T型管路模型Fig.1 Finite element model
管道模型与流体模型网格划分均采用六面体结构画网格,并对流动参数变化较大部位进行了网格加密。耦合模型控制参数,结构模型采用动态隐式分析、大位移小应力模型,流体模型采用瞬态分析。对接触面分别设置流固耦合边界条件,管道两端均采用三维零位移约束,流体入口和出口均为压力边界条件,同时在入口给定初始速度,求解器为稀疏矩阵求解器。
2.2 流固耦合振动特性结果分析
对流固耦合模拟结果进行后处理,得到管内流体速度分布矢量图,并对局部进行放大如图2所示。据图可知,流体速度在T型接合处存在一个复杂的速度分布场,即在迎流面轴线附近形成一个低速区,向两侧快速增大形成2个高速区,在背流面的2个转角处形成2个低速区,同时存在回流涡,这是由于接合处管道结构突变,流体直接冲击管道,管内流体运动方向被强制改变。在90°弯管段内侧流体速度大于外侧流体速度,这是由于弯管段管道结构的连续变化,流体流经弯管时流动方向被迫改变,且内侧流体行程小于外侧流体。T型接合管后两直管内流体速度等于T型接合管前直管内流体速度的二分之一,这是因为T型接合管前后管径相同,分流后一旁支管路的流量为分流前的二分之一,管径不变速度变为原来的二分之一,这与理论相符。

图2 速度分布矢量图Fig.2 Velocity distribution vector
图3给出了管道的应力分布云图,从图中可以看出,在T型接合处存在一个局部高应力区,这是因为在T型接合处流体垂直冲击管道,流体流动方向和流动状态被流道限制而改变,流体对管壁的作用力增大,冲击应力增大。在2个90°弯头的内外两侧都存在局部高应力区,这是因为流体在弯管段流动状态发生了改变,流体对管壁不同位置的作用力不相等,同时弯管处流体流动状态引起的压力变化对弯管具有拉直效应。长期高应力会导致管道焊缝开裂失效、疲劳破裂造成介质泄露,因此,为保证T型管道系统安全运行需对T型接合部和弯头进行加强,同时对这些部位进行重点监测。
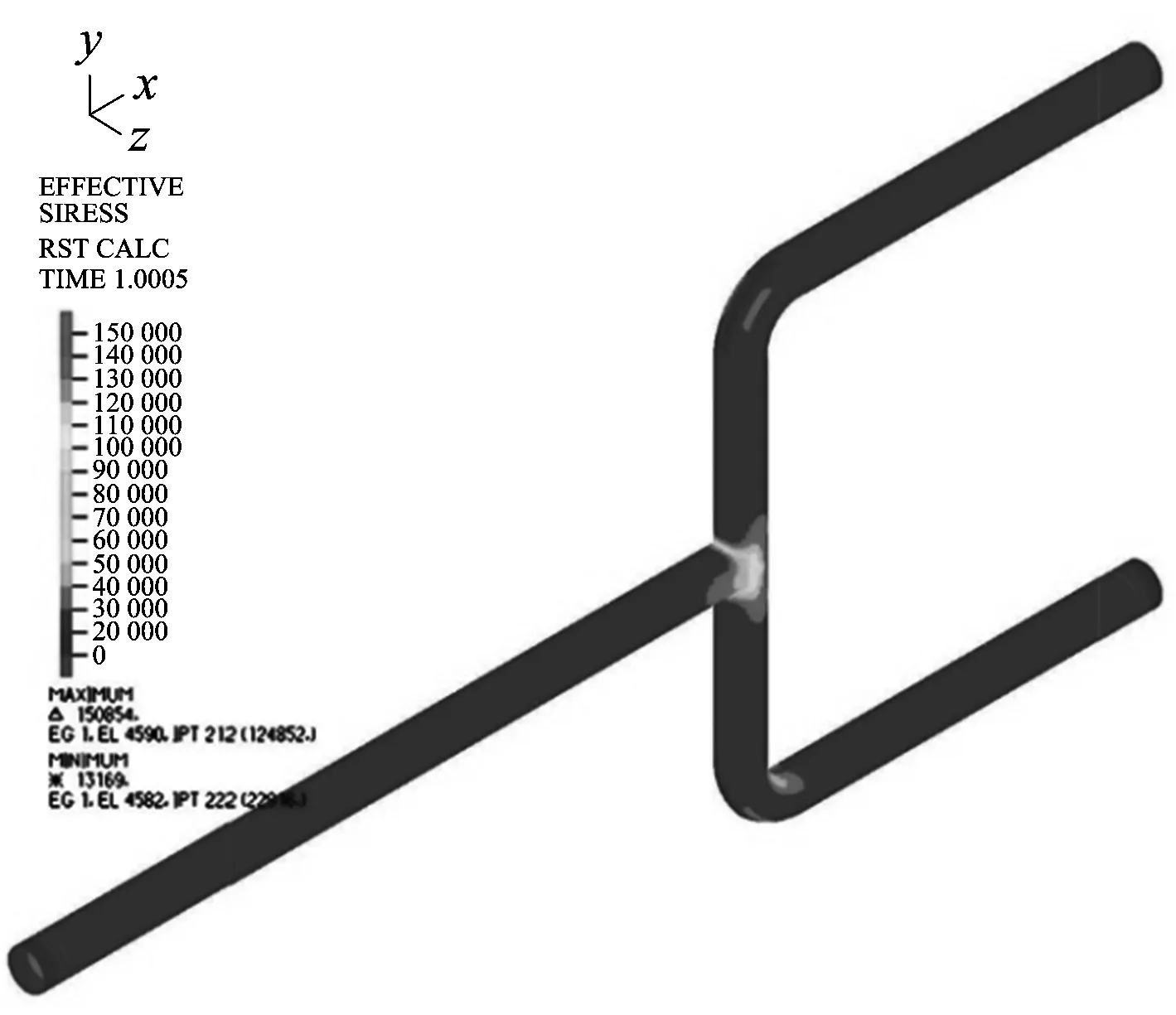
图3 应力分布云图Fig.3 Stress distribution cloud
图4给出了管道振动的位移分布云图以及位移在X,Y,Z3个方向的分量云图,从图中可以明显的看出,在T型结合处位移达到最大,在90°弯管处位移逐渐增大。对比X,Y,Z3个方向的位移分量图可知,流体激励引起的管道耦合振动在X,Y,Z3个方向具有不同的强度,同时,振动强度的分布规律也存在很大的差异。X,Z方向的振动主要体现在T型结合部,Y方向的振动主要体现在90°弯管及其后的直管段。说明流体流经T型管引起的管道振动具有方向性,在不同的方向引起的振动不仅振动强度存在很大差别,而且分布规律也存在很大的不同。

图4 位移分布云图Fig.4 Displacement distribution cloud
瞬态流固耦合计算可得管道振动加速度随时间的演变过程,在T型管上取4个不同截面,截面分布如图5所示。提取截面上的加速度信号,在MATLAB中编制程序进行傅里叶变换得到对应截面加速度信号的频谱图,如图5所示,图中纵坐标为振动幅度,单位为m·s-2;横坐标为频率,单位为Hz。频谱图(a),(b),(c),(d)分别对应截面A1,A2,A3,A4的加速度信号。

图5 截面分布Fig.5 Cross section profile
从图6数值模拟加速度频谱图可知,在频谱图的0点位置附近出现了峰值频率,这是因为流体流动参数变化引起了管道振动,管道在振动过程中偏离了初始位置,所以此峰值频率不是结构的响应频率,这与文献[17]的结论相符。响应频率为258.5 Hz时振动幅值远远大于其他峰值频率,说明响应频率为258.5 Hz时的振动能量远大于其他频率振动能量。

图6 数值模拟加速度频谱Fig.6 Numerical simulation of acceleration spectra
从图6数值模拟得到的加速度信号频谱图可得结构振动的响应频率,前五阶响应频率如表1所示。

表1 结构响应频率(流固耦合模拟)
管道系统内部有流体作用和无流体作用时存在很大的差别,为说明流固耦合对管道影响,对相同支撑条件下的管道进行了结构模态分析,管道的前五阶固有频率如表2所示。

表2 结构固有频率(固体模态分析)
对比表1流固耦合结构响应频率和表2管道固有频率可知,考虑流固耦合作用与不考虑流固耦合作用管道响应频率相差很大,说明流体介质对T型管的振动特性有着显著影响,T型输液压力管道内存在明显的流固耦合效应,这是因为流体流经结合部时,流体压力失稳诱发流体与结构之间强烈的结合部耦合以及流体压力与管壁应力之间的泊松耦合,在弯管处流动状态被强制改变,诱发了对弯管具有“拉直”效应的Bourdon耦合。
3 试验测试
3.1 试验器材
针对T型管内部流动参数变化引起的管道振动开展试验,试验装置结构示意如图7所示。试验中使用的数据采集设备为杭州亿恒科技有限公司的AVANTMI-7016数据采集与分析仪,压力传感器为江东精诚自动化设备有限公司生产的BP8100A散硅压力变送器,加速度传感器为PCB352C33加速度传感器,空气压缩机为AV-0.17/8型压缩机,流量计为LUGB-MIK-Y 20 KDSXCN型涡街流量计,储气罐(1 000 L)。

图7 试验装置结构Fig.7 Structure diagram of the test device
3.2 试验结果分析
3.2.1试验环境信号分析
在振动测试中共检测了4个测点(A1,A2,A3,A4)的加速度信号,4个测点分别与图4中的4个截面相对应。
试验测得的信号不仅包含管道耦合振动信号,还包含环境振动信号。因此,试验环境对试验测试结果的准确性有很大的影响,为排除环境的振动信号对试验结果的影响,在试验开始前对环境的振动信号进行了测试。借助MATLAB软件编程对测得的环境振动信号进行傅里叶变换,得到4个测点的环境信号的频谱图,如图8所示,频谱图(a),(b),(c),(d)分别对应测点A1,A2,A3,A4振动信号的频谱分析结果。

图8 环境信号频谱Fig.8 Environmental signal spectrum
对比分析4个测点环境振动信号的频谱图,可知该试验环境存在明显的环境振动,振动频率分别为8,27.5,75.5和118 Hz,此外还有50 Hz的倍频振动,即:
f=50·NN=1,2,3…
(10)
从图8环境信号频谱图可以清楚的看出,环境振动频率在低频段具有很大的振幅,在较高频段振幅很小,说明环境振动在低频段具有很高的能量,在高频段振动能量很小,即,环境振动对低频段试验信号干扰较大,对高频段的干扰很小。所以,在处理试验信号时要重点关注环境振动对低频信号的干扰。
3.2.1试验信号分析
试验测点与环境振动测点具有相同的分布,调节控制阀使试验工况与数值模拟相一致,测定该状态下4个测点的振动信号。将试验测得的振动信号运用MATLAB编程进行傅里叶变换,得到4个测点振动信号的频谱图,如图9所示,频谱图(a),(b),(c),(d)分别对应测点A1,A2,A3,A4振动信号的频谱分析结果。
从图9试验信号频谱图可知,4个测点振动信号的频谱线走势基本相同,在低频段环境振动频率很强,高频段环境振动频率不明显,说明流体诱发的管道振动在低频段的能量低于环境振动能量,在高频段环境振动的能量远低于流体诱发的管道振动的能量。对比发现频谱图(c)与(a),(b),(d)存在较大的差别,这是因为测点A3测定的是T型管在Y方向的加速度,而测点A1,A2,A4测定的是T型管在X方向的加速度。

图9 试验信号频谱Fig.9 Test signal spectrum
对比图8和图9得试验工况下流体诱发管道振动的前五阶响应频率如表3所示。

表3 试验响应频率
从图9不同测点的频谱图可知,不同测点同一频率的振动幅度存在较大的区别,即同一阶频率在不同测点的振动能量不同,说明各阶频率的振动能量的分布与位置有关。
4 模拟与试验对比分析
将数值模拟得到的流固耦合频率与相应工况下的试验频率列表分析,如表4所示。

表4 频率对比分析
从表4数值计算得到的流固耦合频率与试验频率对比可知,流固耦合频率与试验频率存在一定的误差,这是因为在建立管道模型时,根据实际的管道系统对模型进行了适当的简化:忽略管道系统中法兰质量;管道材料属性均匀;管道系统采用槽钢支撑,支撑刚度很大,模拟时按固支处理。虽然数值计算频率与试验频率存在一定的误差,但总体上吻合较好。证明了流固耦合模拟用于计算管道系统的可行性与准确性。
5 结论
1)T型输流管道在输送流体的瞬变过程中形成了一个非定常流场,流体流动参数变化引起管道的振动,造成管道部分区域出现应力集中和形变,即输送流体介质的压力管道内存在明显的流固耦合效应。
2)通过流固耦合数值计算可以得到压力管道的振动特性参数。计算结果表明,压力管道各阶特征频率在不同位置的振幅存在较大差异,即各阶振动频率在不同的位置的振动能量不相同,说明各阶频率的振动能量与位置有关。
3)通过将数值模拟和试验结果进行对比可知,考虑了流固耦合效应的数值计算得出的压力管道振动特征频率较为准确,除了用于深入研究流固耦合振动机理之外,也具有工程应用价值,是预测压力管道特征频率和进行管道振动故障诊断的有效方法。
[1]Pramila, A., J. Laukkanen and S. Liukkonen. Dynamics and stabilityof short fluid-conveyin Timoshenko element pipes[J]. Journal of Sound & Vibration, 1991,144(3): 421-425.
[2]周建新, 吴轩,郭再富.美国管道事故对我国油气管道安全的启示[J]. 中国安全生产科学技术, 2014,10(S1): 73-78.
ZHOU Jianxin,WU Xuan,GUO Zaifu. Enlightenment from incidents of oil and gas pipeline in USA[J].Journal of Safety science and Technology,2014,10(S1):73-78.
[3]刘延雷, 陈涛,杨志军,等.可变径管道漏磁检测有限元仿真与实验研究[J]. 中国安全生产科学技术, 2016,12(12): 42-47.
LIU Yanlei, CHEN Tao,YANG Zhijun,et al. Finite element simulation and experimental research on variable diameter pipeline magnetic flux leakage nondestructive testing[J].Journal of Safetyscience and Technology,2016,12(12):42-47.
[4]李著信,苏毅,吕宏庆,等.管道在线检测技术及检测机器人研究[J]. 后勤工程学院学报, 2006,22(4): 41-45.
LI Zhuxin,SU Yi,LYU Hongqing, et al. Research of pipeline on-line detection technology and detection robot[J]. Journal of logistics Engineering University, 2006,22(4):41-45.
[5]赵则祥, 王延年,朱强.长输油气管道泄漏检测方法[J]. 中原工学院学报, 2008,19(5): 10-14.
ZHAO Zexiang,WANG Yannian,ZHU Qiang. Pipeline leakage detection mothed for long oil and gas pipelines[J]. Journal of Zhongyuan University of Technology, 2008,19(5):10-14.
[6]Feng, Y., X. Wang and D. Zhao. Investigation and Analysis of Pipeline Accidents[J]. China Offshore Oil & Gas,1999.
[7]Jin, W.L., et al.Cause Analysis and Countermeasure for Submarine Pipeline Failure[J]. Bulletin of Science & Technology, 2004.
[8]冯卫民,宋立,肖光宇. 基于ADINA的压力管道流固耦合分析[J]. 武汉大学学报(工学版),2009,42(2): 264-267.
FENG Weimin,SONG Li,XIAO Guangning. Coupling analysis of fluid-structure interaction in pressure pipes based on ADINA[J]. Engineering Journal of Wuhan University,2009,42(2):264-267.
[9]刘昌领,罗晓兰,叶道辉,等. 一端固定一端简支输流管道流固耦合振动分析[J]. 设计与研究,2013(7): 19-23.
LIU Changling, LUO Xiaolan,YE Daohui,et al. Vibration analysis of liquid-filled pipes with fixed-hinged under fluid structure interaction[J]. Design and Research,2013(7):19-23.
[10]李宝辉,高行山,刘永寿,等. 两端固支输流管道流固耦合振动稳定性分析[J]. 机械设计与制造,2010(2): 105-107.
LI Baohui, GAO Xingshan,LIU Yongshou, et al. The stability analysis of liquid-filled pipes with fixed bearing at both end under FSI vibration[J]. Machinery Design and Manufacture Jixie Sheji yu Zhizao,2010(2):105-107.
[11]张毅鹏,侯建华,宋贝贝,等. 圆弧输流管道流固耦合力学特性分析[J]. 河南建材,2014(3): 29-30.
ZHANG Yipeng, HOU Jianhua,SONG Beibei,et al. Analysis of fluid-solid coupling mechanical properties of circular arc pipeline[J].Henan Building Materials,2014(3):29-30.
[12]徐合力,蒋炎坤.弯曲输流管道流固耦合流动特性研究[J]. 武汉理工大学学报(交通科学与工程版),2008,32(2): 343-346.
XU Heli,JIANG Yankun. Research on fluid-solid coupling flow characteristics of curved pipelines[J].Journal of Wuhan University of Technology(Transportation Science and Engineering),2008,32(2):343-346.
[13]俞树荣,马璐,余龙.弯曲输流管道流固耦合动力特性分析[J]. 噪声与振动控制,2015, 35(4): 43-47.
YU Shurong,MA Lu,YU Long. Analysis of dynamic characteristics of fluid-structure interaction in curved infusion pipelines[J].Noise and Vibration Control,2015,35(4):43-47.
[14]张杰,梁政,韩传军. U型充液管道的流固耦合分析[J]. 应用力学学报,2015(1): 64-68.
ZHANG Jie,LIANG Zheng,HAN Chuanjun. Analysis of fluid-structure interaction of U-type liquid pipelines[J]. Chinese Journal of Applied Mechanics,2015(1):64-68.
[15]许伟伟,武博,吴大转,等.非稳定流体与U形管路耦合振动特性研究[J]. 高校化学工程学报,2012(5): 770-774.
XU Weiwei, WU Bo,WU Dazhuan,et al.Vibration investigation of U pipe interacted with unsteady fluid[J].Journal of Chemical Engineering of Chinese Universities,2012(5),770-774.
[16]丁毅,陈立民.基于 CFX-ANSYS的灌装头斜 T型管接头的流固耦合分析[J]. 包装工程,2011,1(15): 85-87.
DING Yi,CHEN Limin. Flow-structure interaction analysis for the inclined T-tube joint of filling head based on CFX-ANSYS [J].Packaging Engineering,2001,1(15):85-87.
[17]张艳萍,徐治萍,刘土光,等.输液管道流固耦合的响应分析[J]. 中国舰船研究,2006,1(3): 66-69.
ZHANG Yanpin, XU Zhiping,LIU Tuguang,et al. Response analysis of fluid-structure interaction in pipelines Transporting fluids[J].Chinese Journal of Ship Research,2006,1(3):66-69.

