复杂网络同步系统牵制控制器设计
郑步秋,胡俊强
(1.湖南华菱湘潭钢铁有限公司 五米宽厚板厂,湘潭 411101;2.湖南工程学院 电气信息学院,湘潭 411104)
复杂网络同步系统牵制控制器设计
郑步秋1,胡俊强2
(1.湖南华菱湘潭钢铁有限公司 五米宽厚板厂,湘潭 411101;2.湖南工程学院 电气信息学院,湘潭 411104)
针对复杂网络系统,研究此类系统的同步控制问题.利用牵制原理,牵制系统部分节点,运用Lyapunov稳定性理论并结合矩阵不等式处理方法,得出了复杂网络系统同步牵制控制器存在的充分条件.同时得出了牵制节点数和牵制控制增益大小之间的关系图.最后给出两个数值仿真说明其有效性.
复杂网络,同步,牵制控制
复杂网络广泛存在于自然界与人类社会的各种现象中.由于其应用广泛及其理论研究方法的不断突破,复杂网络已成为物理学、信息学、化学、生物学、医学、管理学、社会学等学科研究的热点课题.
复杂网络系统节点同步[1-13]是自然网络和社会网络的一个重要特性,也是复杂网络系统中一个基本的现象,在对复杂网络系统同步过程的研究中,一方面是研究复杂网络系统的自同步特性,另一方面是研究设计控制器,研究复杂网络系统的同步控制问题.针对复杂网络同步控制问题,许多控制方法被运用,如脉冲控制方法[3-7]、自适应控制方法[8-11]以及它们之间的组合控制方法[12-13]被广泛运用作用于混沌系统.同时,在实际生活中,对于一个实际的复杂网络系统,如人体的大脑、神经网络,自然界中的生态网络,等等此类系统,其网络中节点数是不可数的,在设计控制器的过程中若针对每个节点,则这既是一件繁琐,同样也是一件不容易完成的事.针对这种情况,牵制控制就应运而生,其控制思想是控制系统的部分节点,通过节点间的相互作用,进而达到控制整个网络,使系统达到同步稳定的目的.
近年来,由于复杂网络理论的发展,涌现出许多利用牵制控制原理,设计牵制控制器,使复杂网络系统达到同步稳定的相关研究[14-15].但是,针对一个节点众多的复杂网络系统,设计牵制控制器时,节点的选取问题,即在复杂网络系统中,选取哪些节点的问题、选择节点数量的问题、以多大的控制增益实现控制的问题等一直是研究复杂网络牵制控制中的一个亟待解决的问题.
基于上述,本文针对复杂网络系统,利用牵制控制原理,选取度较高的节点进行控制,运用Lyapunov稳定性理论并结合矩阵不等式处理方法,得出复杂网络系统同步牵制控制器存在的充分条件,同时,得出了复杂网络系统中控制节点的数目与控制增益大小之间的关系图,最后给出数值仿真说明其有效性.
1 问题描述
考虑如下复杂动态网络:
(1)
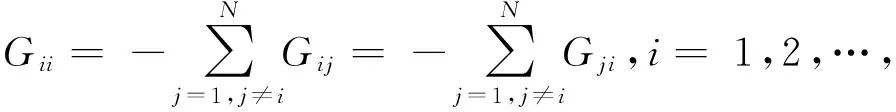
假设1:文献[16]在系统(1)中,存在一个正数l,对光滑非线性函数f(·)满足下面Lipschitz条件
||f(a)-f(b)||≤l||a-b||
(2)
其中a,b∈R,||·||表示欧几里得范数.

①S<0,


定义1:若一个网络达到渐进同步,则
x1(t)=x2(t)=…=xN(t)=s(t),t→
(3)
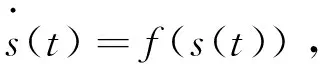
ei(t)=xi(t)-s(t)
(4)
从等式(4)和系统(1),我们可以得到如下误差系统
=1,2,3,…,N
(5)
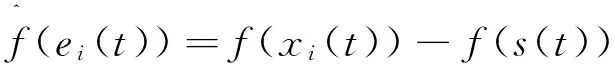
2 牵制控制器设计
对于一个具有众多节点数目的复杂网络系统,通过控制每个节点使系统同步往往得不偿失且难度很大.所以,针对此类复杂网络系统,利用牵制控制原理设计控制器是一种有效的控制途径,在具体实现的过程中,即通过控制系统度较高的节点进而控制整个网络,使其同步.在这一节,主要任务是设计复杂网络系统牵制控制器,具体将系统分为牵制控制部分和被牵制控制部分两部分.对牵制控制部分设计控制器,这样,误差系统(5)就变为:
(6)
改写成矩阵形式为:
(7)

为了使系统达到同步稳定状态,针对系统(1),设计如下反馈控制器,当所设计的控制器使误差系统(6)渐进稳定时,即系统(1)达到同步.
ui(t)=kiei(t)
(8)
定理1:在假设1条件下,l为正常数,当存在对角矩阵K满足下列条件时,
(9)
则误差系统(5)渐进稳定,即系统(1)达到网络间同步状态.
证明:构造李雅普诺夫函数为:
(10)
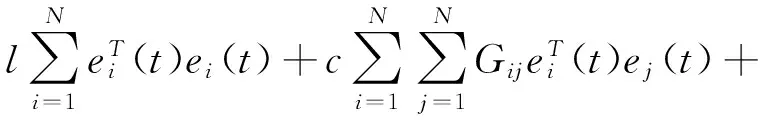
令:K=diag(k1,k2,…,kL),则:


由系统(7)有
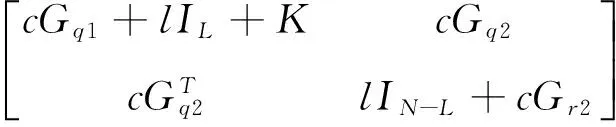
由定理1中(9)式,可知系统渐进稳定.由此,定理1得证
对(9)式,由引理1可得,
lIN-L+cGr2<0
cGq1+lIL+K-cGq2
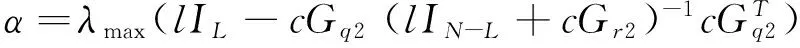
推论1:在假设1条件下,当复杂网络系统存在无牵制控制节点,利用引理1,取l为正常数,对系统每个节点,当存在控制增益k满足下列条件时,
lIN-L+cGr2<0
cλmax(Gq1)+k+α<0

3 数值示例
针对一个包含20个节点,其中每个节点包含3个变量的复杂网络系统:

给定系统耦合强度参数c=2.15;设有非线性界函数的最大值l=5;G∈R20×20为满足条件的耦合矩阵;在给定参数条件下,由定理1和推论1,可得出如下控制节点数与最低控制增益的离散曲线图.
由图1,取牵制控制节点数为12,各牵制节点控制增益满足k<-10,可得出图2牵制节点状态曲线图和图3被牵制节点状态曲线图.

图1 牵制节点数与最低控制增益曲线图

图2 牵制节点状态曲线图
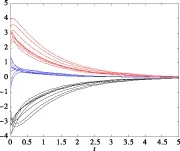
图3 被牵制节点状态曲线图
由图1~图3可知,经过一段时间后系统状态达到稳定状态.
4 小结
本文研究了一类复杂网络模型的同步牵制控制,得出了牵制控制节点数与控制增益的关系图,运用Lyapunov稳定性理论并结合矩阵不等式处理方法,得到了复杂网络系统同步牵制控制器存在的充分条件.最后给出数值仿真说明其有效性.
[1] D.J.Watts, S.H.Strogatz. Collective Dynamics of “Small-world”Networks[J]. Nature,1998,393(6684):440-442.
[2] L. M. Pecora, T. L. Carroll. Synchronization in Chaotic Systems[J]. Phys.Rev.Lett, 1990, 64(8):821-824.
[3] B.Liu, X.Z.Liu, G.R.Chen, H.Y.Wang. Robust Impulsive Synchronization of Uncertain Dynamical Networks[J]. IEEE Trans.Circuits Syst. I, Reg. Papers, 2005, 52(7):1431-1441.
[4] H.B.Jiang, Q.S.Bi. Impulsive Synchronization of Networked Nonlinear Dynamical Systems[J]. Phys. Lett. A, 2010, 374(27):2723-2729.
[5] Z.H.Guan, Z.W.Liu, G.Feng, Y.W.Wang. Synchronization of Complex Dynamical Networks with Time-varying Delays Via Impulsive Distributed Control[J]. IEEE Trans. Circuits Syst. I, Reg. Papers, 2010, 57(8):2182-2195.
[6] Y.W.Wang, M.Yang, H.O.Wang, Z.H.Guan. Robust Stabilization of Complex Switched Networks with Parametric Uncertainties and Delays Via Impulsive Control[J]. IEEE Trans. Circuits Syst. I, Reg. Papers, 2009, 56(9):2100-2108.
[7] J.Q.Lu, D.W.C.Ho, J.D.Cao. A Unified Synchronization Criterionfor Impulsive Dynamical Networks[J]. Automatica. 2010, 46(7):1215-1221.
[8] L.Wang, H.P.Dai, H.Dong, Y.H.Shen, Y.X.Sun. Adaptive Synchronization of Weighted Complex Dynamical Networks with Coupling Time-varying Delays[J]. Phys. Lett. A,2008,372(20):3632-3639.
[9] J.Zhou, J.A.Lu, J.H.Lu. Adaptive Synchronization of an Uncertain Complex Dynamical Network[J]. IEEE Trans.Autom.Control, 2006, 51(4):652-656.
[10]H.Liu, J.Chen, J.A.Lu, M.Cao. Generalized Synchronization in Complex Dynamical Networks Via Adaptive Couplings[J]. Phys. A, Stat. Mech. Appl, 2010,389(8):1759-1770.
[11]Y.H.Xu, W.N.Zhou, J.A.Fang, H.Q.Lu. Structure Identification and Adaptive Synchronization of Uncertain General Complex Dynamical Networks[J]. Phys. Lett. A, 2009, 374(2): 272-278.
[12]Z.Li, G.R.Chen. Robust Adaptive Synchronization of Ncertain Dynamical Networks[J]. Phys.Lett.A, 2004, 324(2/3):166-178.
[13]K.Li, C.H.Lai. Adaptive-impulsive Synchronization of Uncertain Complex Dynamical Networks[J]. Phys.Lett.A, 2008, 372(10):1601-1606.
[14]X.Li, X.F.Wang, G.R.Chen. Pinning a Complex Dynamical Network to Its Equilibrium[J]. IEEE Trans.Circuits Syst. I, 2004, 51(10):2074-2087.
[15]W.W.Yu, G.R.Chen and J.H.Lue. On Pinning Synchronization of Complex Dynamical Networks[J]. Automatica, 2009, 45(2):429-435.
[16]Tae H.L, Ju H.P, D.H. Ji, O.M.Kwon, S.M. Lee. Guaranteed Cost Synchronization of a Complex Dynamical Network Via Dynamic Feedback Control[J]. Applied Mathematics and Computation, 2012, 218:6469-6481.
[17]Boyd S, Ghaoui L EI, Feron E. Linear Matrix Inequalities in System and Control Theory. Philadelphia,PA:Society for Industrial and Applied Mathematics,1994.
Synchronization of Complex Network Systems with Pinning Control
ZHENG Bu-qiu1,HU Jun-qiang2
(1.Hunan Valin Xiangtan Iron & Steel Co., Ltd., Xiangtan 411101, China;2.College of Elect. and Information, Hunan Institute of Engineering, Xiangtan 411104, China)
The synchronization control problem of some general complex dynamical networks is investigated. The pinning control theory is used to make the system achieve synchronization. Bases on Lyapunov stability theory and combined with matrix inequality, a sufficient condition for the existence of the complex network systems is obtained. At the same time, the relationship between the number of pinning nodes and the control gain is established. Finally, a numerical example is given to demonstrate the feasibility of proposed method.
complex network; synchronization; pinning
2016-09-15
郑步秋(1972- ),男,工程师,研究方向:五米宽厚板钢材成型,复杂网络系统.
O157.5
A
1671-119X(2017)01-0024-04

