基于脆弱性的地铁网络事故蔓延模型构建研究*

许　葭，宋守信，翟怀远，陈明利

(北京交通大学 经济管理学院，北京 100044)

0　引言

通常意义上，只有当事故或灾害不可避免时，我们才会相对应的采取一定的应急救援工作来防止事故蔓延并减轻危害后果，但是无论是从应急救援的管理思路[1-2]，还是具体实施上[3]，我们的着眼点仍然集中在事故发生点。然而，随着现代社会的不断发展，社会中各部分不再仅仅是以单一个体存在，更多的呈现出系统化、互联化的特色，特别是新兴的地铁系统，牵一发而动全身，正因为如此，迫切需要能与之相切合的科学应急管理方案。为此，首要任务就是针对网络化地铁系统事故蔓延的机理开展研究。

事实上，风险的传递[4]、舆论的传播[5]、事故的蔓延等多种网络条件下的蔓延动力学已经成为研究热点[6]，近些年来更是成果颇多，例如：文献[7]结合主动网络节点，双稳态元素和链路延迟交互的特征，提出故障传播动力学模型；文献[8]针对供水系统、供电系统、交通系统的共同特征，建立1个普适性的灾害蔓延动力学模型，主要涉及网络结点的自修复功能、灾害蔓延机制和内部随机噪声3个重要特征参数；文献[9]基于另1个普适性的灾害蔓延动力学模型，对3种网络拓扑结构(随机网、小世界网和无标度网)进行仿真，结果显示3种网络表现出不同的脆弱程度，并获得实例验证。

总结以上研究结果，更多关注的是整个系统的运行状态，是相对宏观的角度，但是在安全领域，特别是应急措施的制定，则更需要关注节点自身的层面。因此，针对地铁节点数量少，且网络平均度小的特点，有针对性提出在地铁网络上事故蔓延的机理，并据此完成模型构建。

1　原理阐述

1.1　脆弱性

脆弱性研究起源于环境科学[10]领域，随后扩展到电网、交通等多个领域，对于脆弱性概念，不同研究领域的认识相对统一，即脆弱性是个概念的集合，既考虑系统内部条件对脆弱性的影响[11]，也包含系统与外界环境相互作用的特征[12]，具体而言，脆弱性有以下2个特点：

1)脆弱性是针对系统本身

脆弱性是系统本身的特质，它的着眼点不是系统中任何1个单一用户，而是1个系统的整体。它不仅限于每个用户个体的使用感受，不拘泥于系统中每个部件的完美运行，更多的是考虑作为1个整体的系统能否正常运行，所以从某种意义上来说，系统脆弱性可以看成是对系统可靠性的宏观视角下的补充，而非对立存在。

2)脆弱性是复杂概念集合

随着安全领域的不断深入研究，仅仅针对单一事物的研究、评价已经远远不能满足现在安全管理的需求，如何科学、准确表述复杂耦合系统下的安全现状，是安全研究的难点和重点，脆弱性正是在此情况下被广泛提及，并且被证明是有效的。脆弱性既需要考虑系统内部条件对系统脆弱性的影响，也包含系统与外界环境相互作用的特征，所以脆弱性是1个包含了系列相关概念的概念集合，各个概念间也不是简单的叠加，彼此之间存在着复杂的耦合关系。

脆弱性的以上特性，使得使用脆弱性概念来全面刻画地铁的安全状态，特别是用来考虑事故的蔓延，是可行的。

1.2　事故蔓延机理

在网络化的情况下，各节点间不再是孤立存在的，而是存在着紧密的相互联系。因此，事故一旦在网络中发生，那将不可避免地沿着网络拓扑结构进行蔓延，如图1所示。

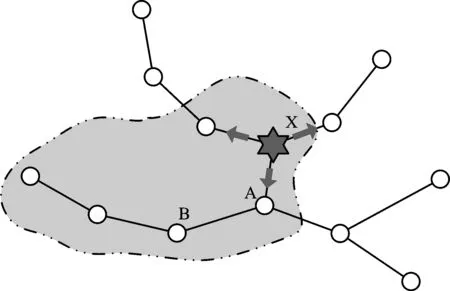
图1　网络事故蔓延示意Fig.1　Schematic of failure propagationin network

也就是说，事故点会对整个网络系统中的所有站点产生影响，这是地铁事故蔓延机理的1个特点—普遍性。

与此同时，网络中事故蔓延的基本原则毫无疑问是拓扑距离的远近[13]，离事故点最近的节点，譬如图1中的节点A与节点B，节点A必定会先受到影响，之后影响节点B。换言之，事故点产生的影响并不是同时发生，而是根据路径的长短，存在一定的先后顺序，这是地铁事故蔓延机理的另1个特点—顺序性。但是否会在节点A处引发事故，就需要考虑节点A本身的性质，也就是节点A的脆弱性。

根据上述的思路，事故在节点X发生，首先影响离事故初发点X的拓扑距离为1的所有节点的集合，其次为拓扑距离为2的节点，并逐步扩散至整个网络。如果被影响节点的脆弱性足够低，那么这些扰动就会在节点里逐渐被吸收；反之，如果此时节点的脆弱性较高，那么扰动就会外在表现出来，影响站点的运营状态，最终出现在图1中显示的深色事故区域。因此，在地铁网络上，事故蔓延呈现出第3个特点—指向性，也就是事故的发展不是均匀的，而是倾向于往脆弱性大的站点蔓延。

2　模型构建

2.1　引力模型

17世纪牛顿提出著名的万有引力定律，由此牛顿物理学问世。万有引力定律给物理学及许多自然科学学科的发展以划时代的推动。根据该定律，任何2个物体之间的作用(引力)的大小与它的质量成正比，与它们之间的距离平方成反比。引力模型是以牛顿经典力学的万有引力公式为基础，应用广泛的空间相互作用能力模型，即用来分析和预测空间相互作用能力的数学模型，目前已被广泛应用到各种学科领域中，其中比较常见的是国际贸易学说。Tinbergen(1962)和Poyhonen(1963)对其在经济学领域做了发展、延伸，模型在以后很多学者的实证分析方面也得到成功印证。同时，随着经济地理学家的关注，引力模型被广泛应用于各类相关研究中。引力模型的1个重要特点，是它的基本形式保持不变，只要对参数和分量的定义作出适当的改变，就可将引力模型应用于不同的问题。

地铁网络事故的蔓延可以看成站点脆弱性间的引力效应，脆弱性大的站点对于事故初发点之间的吸引力大，引导事故向脆弱性大的地方发展，根据前文提出的3个特点，也符合引力模型的相关结论，所以基于引力模型，构建地铁网络事故蔓延模型。

2.2　地铁网络事故蔓延模型

在地铁系统中，相对于火灾等传统意义上的事故而言，更频繁出现的则是与客流压力相关的事故，例如站点的封站、停运或者通过不停车等。在我国，很多地铁线路长期处于超负荷运行状态，此类事故看似影响不大，但是波及范围广、发生次数多，与此相对的则是安全管理上的忽视，极易产生重大的安全事故隐患。因此，基于引力模型计算地铁网络事故各站点两两间的引力值，此值可以反映出事故在2个站点间传递的难易程度，在此称之为事故蔓延引力值。

将引力模型特别应用于地铁网络事故蔓延上，有针对性地对相应的参数进行修改。首先，上文已经阐述脆弱性在表征安全状态，特别是地铁安全状态时的重要性，所以在地铁网络事故蔓延的引力模型中，使用脆弱性代替质量；其次，关于节点间的距离，在模型中采用地铁实际运营的区间时间，因为在地铁系统中，一方面由于固定的轨道和隧道限制，地铁客流不存在路径上的流失，必然是从节点到节点，另一方面，地铁车辆的运营速度也是存在差异的，所以节点间的区间时间更能说明站点间的互联状态。因此，基于引力模型，构建地铁网络事故蔓延模型，如式(1)所示。

(1)

其中：Fxi为站点i和事故初发点X之间的事故蔓延引力值；VX,Vi分别为事故初发点X和站点i的脆弱性值；tXi为站点i到事故初发点X的最短时间；K为引力系数，在这里选取为1；a,b分别为事故初发点X和站点i对事故蔓延的潜力指数。

对于事故初发点X和站点i，在不同情况下，对事故蔓延的吸引力不同，也就是潜力指数是不同的。当a>b时，说明事故倾向于聚集在初发点X处，换言之，事故点处的应急救援工作相对出色，抑制事故的蔓延；反之，当a

所以根据式(1)，可以得出在事故点X和网络中各个站点之间的引力值大小，按照降序排列的方法绘制曲线，该曲线存在数个断裂点，即在该点附近，微小的变化也会引起引力值较大的改变，换言之，在该点曲线的凹凸性发生变化。由此，该曲线也被分为若干个层次，据此得出事故蔓延到各个站点的层级顺序，可有针对性地采取事故措施。

3　实例应用

以北京地铁为例，截止2015年初，北京地铁共有18条地铁线路，共268个运营车站，其拓扑结构如图2所示。

图2　北京地铁车站拓扑Fig.2　Topology of Beijing subway network

根据文献[14]构建的脆弱性评价模型，可以得到北京地铁各站点的脆弱性数值，由于篇幅限制，选取部分站点，如表1所示。

表1　部分北京地铁车站脆弱性数值

假设站点西直门发生事故，则网络中其余站点到达西直门站的最短时间，采用Floyd算法计算可得，部分数据如表2所示。以磁器口站为例，其到达西直门的最短时间为19 min，所采用的路径为85(磁器口)→43(崇文门)→44(前门)→45(和平门)→46(宣武门)→47(长椿街)→48(阜成门)→49(车公庄)→34(西直门)。

表2　部分北京地铁车站到达西直门站的区间时间

西直门处的脆弱性为3.371 4，明显高于整网的平均值1.428 2，那么取a=1,b=2，根据式(1)可以得出各站点的事故蔓延引力值，如表3所示。为了方便观察各站点事故蔓延引力值的变化情况，对各站点的事故蔓延引力值进行降序排列，与此同时，由于第34位的郭公庄(136，0.092)开始，引力值小于第1位的车公庄(49，4.731)的1.9%，之后的趋势变化相对较小，因此，选取前33位的站点如图3所示。

图3　北京地铁西直门事故蔓延引力值(降序)Fig.3　Failure propagate gravitation of Beijing subway(DESC)

表3　北京地铁车站事故蔓延引力值(西直门)

图4　北京地铁西直门事故蔓延引力值(61-60)Fig.4　Failure propagate gravitation of Beijing subway(61-60)

图5　北京地铁西直门事故蔓延引力值(36-104)Fig.5　Failure propagate gravitation of Beijing subway(36-104)

图6　西直门事故蔓延趋势Fig.6　spreading tendency of Xi Zhimen accident

通过图4和图5明显可以看到在站点62(平安里)、181(大钟寺)和48(阜成门)处出现平稳趋势后，产生较为明显断裂，所以可以据此将事故蔓延分为4个等级，如表4和图6所示。

从上面的结果可以看出，对于同样距离西直门站点拓扑距离为1的35(积水潭)、49(车公庄)、60(动物园)、61(新街口)和181(大钟寺)5个站点就存在明显差距，而在拓扑距离为2的站点中，62(平安里)则相对较为脆弱，甚至超过了部分拓扑距离为1的站点。另一方面，从图6可以较为明显的看出西直门站点的事故是向东南方向蔓延，这与现实的情况较为相符；与此同时，按照模型测算可知，当西直门站点发生客流事故时，需要采取应急响应的站点共有9个，数量较少，有利于制定专项的应急方案。

表4　北京地铁西直门事故蔓延等级

4　结论

1)通过分析脆弱性的内涵特征，确定脆弱性为刻画事故蔓延的特征参数，分析在网络化条件下，地铁事故沿拓扑结构的蔓延机理。

2)与传统地铁网络应急简单依靠地理距离划分不同，根据网络事故蔓延机理，构建基于脆弱性的地铁网络事故蔓延的引力模型，综合考虑脆弱性、拓扑距离、地理距离等多方面因素，为网络条件下客流事故的应急响应等提供相对合理的理论依据。

3)以北京地铁为例，实例验算西直门为初发站点的事故蔓延情况，确定车公庄、新街口、积水潭和平安里4个一级应急响应的站点；鼓楼大街、动物园和大钟寺3个二级应急响应的站点；知春路和阜成门2个三级应急响应的站点。

4)建立的地铁网络事故蔓延引力模型的先决条件为网络中的线路畅通，因而无法应用在火灾等直接破坏线路运营的大型事故上，这将是下一步的重点研究方向。

[1]刘有飞, 蔡斌, 吴素农. 电网冰灾事故应急处理及反思[J]. 电力系统自动化, 2008, 32(8):10-13.

LIU Youfei, CAI Bin, WU Sunong. Emergency management for the ice disaster in power grids and some sugges-tions[J]. Automation of Electric Power Systems, 2008, 32(8):10-13.

[2]高太光, 黄敏, 陈培友. 物联网环境下煤矿救援资源调度多Agent自动协商模型[J]. 管理工程学报, 2016, 30(3):134-140.

GAO Taiguang, HUANG Min, CHEN Peiyou. Multi-Agent automated negotiation model of rescue resource allocation for coal mine accidents based on internet of things[J]. Journal of Industrial Engineering and Engineering Management, 2016, 30(3):134-140.

[3]龚迪琛, 方方, 陈智,等. 核电事故应急随机网络的粒子群优化分析[J]. 原子能科学技术, 2014, 48(5):898-902.

GONG Dichen, FANG Fang, CHEN Zhi, et al. Analysis in nuclear power accident emergency based on random network and particle swarm optimization[J]. Atomic Energy Science and Technology, 2014, 48(5):898-902.

[4]李存斌, 黄旻. 基于学习型贝叶斯网络的供电风险传递分析[J]. 中南大学学报(自然科学版), 2011, 42(8):2338-2344.

LI Cunbin, HUANG Min. Power supply risk transmission analysis based on learning Bayesian networks[J]. Journal of Central South University, 2011, 42(8):2338-2344.

[5]Tsimring L S, Huerta R. Modeling of contact tracing in social networks[J]. Physica A Statistical Mechanics & Its Applications, 2003, 325(1-2):33-39.

[6]Helbing D, Kühnert C. Assessing interaction networks with applications to catastrophe dynamics and dis-aster management[J]. Physica A Statistical Mechanics & Its Applications, 2003, 328(3):584-606.

[7]Peters K 1. Modelling of cascading effects and efficient response to disaster spreading in complex net-works.[J]. International Journal of Critical Infrastructures, 2008, 4(4):46-62.

[8]翁文国, 倪顺江, 申世飞,等. 复杂网络上灾害蔓延动力学研究[J]. 物理学报, 2007, 56(4):1938-1943.

WENG Wenguo, NI Shunjiang, SHEN Shifei,et al. Dynamics of disaster spreading in complex networks[J]. Acta Physica Sinica, 2007, 56(4):1938-1943.

[9]李泽荃, 张瑞新, 杨曌,等. 复杂网络中心性对灾害蔓延的影响[J]. 物理学报, 2012, 61(23):557-563.

LI Zequan, ZHANG Ruixin, YANG Zhao, et al. Influence complex network centrality on disaster spreading[J]. Acta Physica Sinica, 2012, 61(23):557-563.

[10]Schuur E A G, Bockheim J, Canadell J G, et al. Vulnerability of Permafrost Carbon to Climate Change: Implications for the Global Carbon Cycle[J]. BioScience, 2008, 58(8):701-714.

[11]Geneiatakis D, Dagiuklas T, Kambourakis G, et al. Survey of security vulnerabilities in session initiation protocol[J]. IEEE Communications Surveys & Tutorials, 2006, 8(3):68-81.

[12]Gallopín G C. Linkages between vulnerability, resilience, and adaptive capacity[J]. Global Environmental Change, 2006, 16(3):293-303.

[13]汪送, 战仁军. 节点免疫力对事故网络风险传递行为的影响分析[J]. 安全与环境工程, 2015, 22(1):126-130.

WANG Song, ZHAN Renjun. Impact analysis of node immunity on risk transfer behavior in accident network[J]. Safety and Environmental Engineering, 2015, 22(1):126-130.

[14]许葭, 宋守信, 袁朋伟,等. 基于ANP的地铁站点网络脆弱性评价[J]. 中国安全科学学报, 2015, 25(12):129-134.

XU Jia, SONG Shouxin, YUAN Pengwei, et al. Evaluation of network vulnerability of subway stations based on ANP[J]. China Safety Science Journal, 2015, 25(12):129-134.