考虑可靠性要素的应急物流设施选址分配问题的建模研究*

郭咏梅,胡大伟,珠　兰,段澄莹

(长安大学 汽车学院，陕西 西安 710064)

0　引言

在国家应急体系中，应急物流设施的选址分配问题是应急管理理论研究和应急基础设施建设的重要组成部分，应急物流设施的选址是否科学合理，直接关系到社会经济效益和国家防灾减灾系统的运行效率，并且与应急物流系统的时效性紧密相关。

目前，国内外有关应急物流设施选址问题的理论研究还不多，主要是借鉴传统设施选址的思路有针对性地对其进行研究。

国外学者的相关研究起步较早。ALY等[1]以2点间的最短时间作为随机变量，构建意在使应急物流设施数量最少的集合覆盖模型；Geoffrion等[2]总结国内外的研究现状，指出应急设施选址的研究方向；Matsutomi等[3]运用模糊数学的方法研究多目标应急设施选址问题；Ball等[4]对应急物流设施选址的可靠性问题进行分析，认为如果应急物流设施不能在可接受的时间范围内响应受灾点的需求，该设施便是失败的；B. Adenso-Díaz等[5]用资源约束改进传统的应急物流设施选址模型，从而保证受灾点的需求尽可能多的被满足；LI等[6]以最小化运输成本和应急物流设施建设成本为目标，构建1个可靠的固定成本的选址模型。

国内研究主要在“SARS”事件后开始出现，虽起步较晚，但仍取得较为丰富的研究成果。刘洪娟等[7]构建考虑距离、安全性和流量等因素的应急物流多设施选址模型，使模型更具现实意义；张伟[8]从成本最小、加权距离之和最小以及覆盖率最大的角度出发，构建应急物资储备库多目标选址模型；花翠[9]对已有模型和方法的优缺点进行分析，综合利用层次分析法和多目标规划方法，构建应急物流储备库选址模型。

上述研究大多具有关联性，但都没有明确涉及所建立的应急物流设施偶尔不可用的状态，也就是说，已建成的应急物流设施仍然会由于容量限制或是由于灾害的影响而变得不可用的情形。然而，应急物流设施的可用性及可靠性将直接影响受灾点的需求分配和流量分配。国内外学者对应急物流可靠性相关的研究也逐渐发展起来。AN等[10]提出1种基于场景的、随机的混合整数非线性规划模型，可以同时考虑设施中断的风险、交通拥堵以及排队时延等3种情况下的设施选址问题；Li等[11]通过改进的贪婪和拉格朗日松弛算法，求解考虑流量特性的可靠性设施选址问题；Jalali等[12]提出1个考虑可靠性约束的、带有容量限制的双目标设施选址模型；陶莎等[13]考虑到突发事件对道路等的破坏，研究需求和物流网络均不确定的应急物流设施选址问题；朱建明[14]通过将时间作为目标体系的主要参数，重点考虑设施损毁情景下的救援变更时间；付德强[15]建立1个可以保证可靠性的应急物流设施多目标选址模型。总结分析上述相关文献，目前将可靠性的思想用于应急物流设施选址的研究还非常有限，其中对可靠性的表述多单纯基于概率的方法或情形方法。基于此，提出考虑设施可靠性要素的多目标应急物流设施选址模型，将概率方法与情形方法相结合，重点考虑遍历不同数目失效设施的多种情形下的概率，以系统总成本最小和需求覆盖率最大为目标函数，并考虑容量、距离等约束。

1　数学模型

应急物流网络主要考虑应急物流中心和受灾点2类节点间多种物资的运输，需要做出的决策为：在保证最小系统总成本和最大客户需求覆盖率的情况下，确定物流中心的选址区位和各节点间物资分配方案。其中，考虑到开放的设施也存在一定的中断概率，因此以不同情形表示开放设施存在中断的情况。基于以上描述，建立考虑设施可靠性要素的双目标混合整数规划模型。

1.1　符号定义

模型符号定义如表1所示。

表1　模型符号定义

1.2　模型构建

应急物流设施选址分配问题中，考虑设施可靠性要素的双目标混合整数规划模型如下：

(1)

(2)

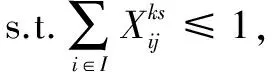
(3)

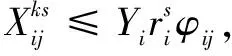
(4)

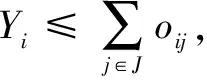
(5)

(6)

(7)

Yi∈{0,1},∀i∈I

(8)

目标函数(1)最小化系统总成本，其中包含建立应急物流中心的固定成本和从物流中心向受灾点运送物资的运输成本；目标函数(2)最大化需求覆盖率；约束条件(3)保证应急物流中心送出的物资得到完全利用；约束条件(4)确保只有被选中建立，且在情形s下启用并能覆盖到受灾点的应急物流中心，才能对受灾点提供物资配送服务；约束条件(5)保证只要是开放的应急物流中心，都可以覆盖至少1个受灾点；约束条件(6)确保由应急物流中心配送给受灾点的物资，不得超过应急物流中心的容量限制；约束条件(7)、(8)对决策变量进行说明。

2　多目标优化算法

目前，多目标优化问题主要由多目标进化算法求解。DEB等[16]在非支配排序遗传算法研究的基础上进行改进，提出1种带精英策略的快速非支配排序遗传算法(NSGA-II)。NSGA-II有效改进非支配排序算法，降低算法计算的时间复杂度，提高算法的求解效率；采用最优保留策略，提高算法的收敛性；采用聚类过程，保持所求解的多样性。借助MATLAB平台自带的函数gamultiobj，实现对提出的多目标应急物流设施选址模型的求解，该函数是基于NSGA-II改进的1种多目标优化算法。MATLAB中基于NSGA-II的多目标优化函数gamultiobj的算法流程如图1所示。

图1　算法流程Fig.1　Algorithm flowchart

3　数值实验

3.1　算例描述

基于控制变量法，构建10组算例以验证所提出模型的正确性。虽然算例中I，J，K较小，但由于情形数S与应急物流中心备选点I的数量呈指数增长，因此S很大，致使算例的计算复杂度O很高。

3.2　参数设置

模型中涉及参数的取值规则如下所示：

1)bi：应急物流中心i的容量水平，取值500。

Fi=α0+α1(bi)+α2(bi)2

(9)

4)S：情形数|S|=2I-1。

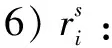
8)坐标生成：备选点i和受灾点j的坐标，由0到100间随机生成，i、j之间的距离dij以欧式距离表示。

10)φij：应急物流中心i对受灾点j的覆盖能力。当应急物流中心的容量水平提升的时候，覆盖函数中的下界lb和上界ub也将增加，因此，应急物流中心也就能覆盖更远距离的受灾点，为其提供配送服务。

φij=

(10)

式中：b为应急物流中心最低的容量水平，取b=200。

11)oij：0-1变量。若φij≠0，则为1；否则为0。

3.3　求解结果

在MATLAB 2014a中运行基于NSGA-II的多目标优化算法，求得10组算例的结果，如表2所示：

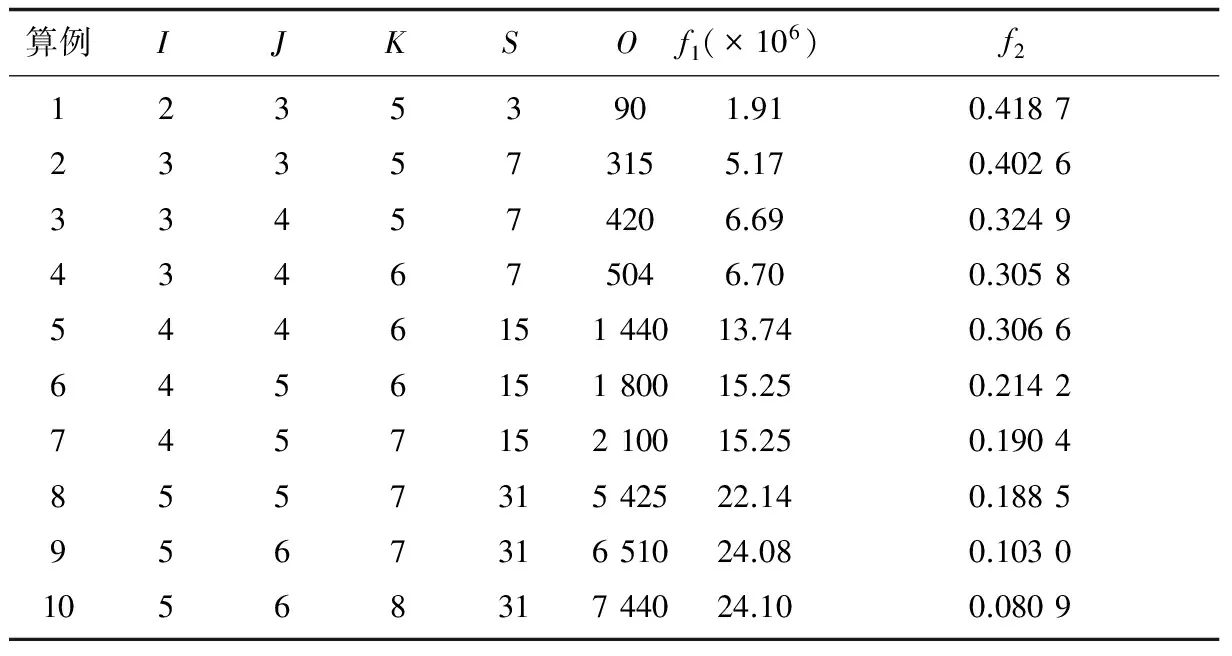
表2　算例求解结果

从上述求解结果可以看出，对于目标函数f1而言，f1逐渐增大。其中，当I增大，J和K不变的时候，f1大幅增加，主要是由新建立的物流中心的固定成本较大所引起的；当J增大，I和K不变的时候，f1小幅增加，主要是由新增加的受灾点与应急物流中心间的运输成本所引起的。对于目标函数f2而言，f2逐渐减小。其中，当J增大，I和K不变的时候，f2大幅减少，主要是由于在应急物流中心数量一定的情况下，受灾点增多，致使应急物流中心能满足受灾点的需求比率降低；当K增大，I和J不变的时候，f2小幅减少，主要是由于应急物流中心内物资数量一定，当受灾点对物资的需求增多时，应急物流中心能满足受灾点对物资的需求比率就会降低。

此外，程序运行得到各算例的帕累托前沿，以算例3的求解结果为例，如图2所示。

图2　算例3帕累托前沿Fig.2　Paretosolution of the case 3

从图2可以得出：系统总成本越高，需求覆盖率也越大，是符合常识的。同时，这些点满足 Pareto 解集的定义：没有任何1个解，在2个目标上都比其余任何1个解占优。

为了进一步分析参数—设施中断概率q，对目标函数的影响，对q进行灵敏度分析，q的取值基于默认值0.02，以步长0.005增大或减小，分析结果如图3所示。

图3　q灵敏度分析结果Fig.3　Result of the q sensitivity analysis

对q的灵敏度分析体现2个目标之间的悖反关系。目标函数f1随着q的增加而小幅度增加，是由于f1由应急物流中心建立的固定成本和从物流中心向受灾点运送物资的运输成本构成，其中固定成本占大部分。考虑到当设施中断概率增加时，并不会影响固定成本部分，仅是由于中断致使的重新分配而产生的运输成本发生变化，因此f1仅是小幅度增加。目标函数f2随着q的增加而减少，是由于当设施中断概率增加时，就会有更多的设施处于不可用的状态，而受灾点对物资的需求不变，这就导致了物流中心对受灾点的需求覆盖降低。

4　结论

1)提出1个有容量限制的双目标应急物流设施选址分配模型，模型目标中引入“需求覆盖率”概念，旨在寻求能综合考虑不同设施发生中断情形的、权衡考虑救灾成本与需求满足程度的近似最优Pareto解集，以最大限度的降低系统总成本，并最大限度的提高应急物流中心对受灾点的需求覆盖率。

2)由于提出的双目标模型属于NP难问题，采用NSGA-II算法对所提出的模型进行求解，并借助MATLAB平台实现对上述模型的求解。求解结果体现灾害发生时，应急物流设施需求覆盖率与系统总成本的关系。此外，对设施中断概率参数q进行灵敏度分析，结果体现设施中断概率存在的不可靠性，对系统总成本以及需求覆盖率的影响。

3)研究内容为灾害发生后，救援系统救灾成本和受灾点需求满足程度的权衡优化，提供可参考的思路。

[1]ALY A, WHITE J. Probabilistic formulation of the emergency service location problem[J]. The Journal of the Operational Research Society, 1978, 29(12): 1167-1179.

[2]Geoffrion A M, Powers R F. Twenty years of strategic distribution system design: an evolutionary perspective[J]. Interfaces, 1995, 25(5):105-127.

[3]Matsutomi T, Ishii H. An emergency service facility location problem with fuzzy objective and constraint[A]// IEEE International Conference on Fuzzy Systems[C]. IEEE Xplore, 1992:315-322.

[4]Ball M O, Lin F L. A reliability model applied to emergency service vehicle location[J]. Operations Research, 1993, 41(1):18-36.

[5]B. Adenso-Díaz, F. Rodríguez. A simple search heuristic for the MCLP: Application to the location of ambulance bases in a rural region[J]. Location Science, 1997, 25(2):181-187.

[6]LI Xiaopeng, OUYANG Y. A continuum approximation approach to reliable facility location design under correlated probabilistic disruptions[J]. Transportation Research Part B-methodological, 2010, 44(4): 535-548.

[7]刘洪娟，罗挺，姜玉宏，等．基于遗传算法的应急物流多设施选址模型研究[J]．后勤工程学院学报，2010，26(3)：46-50．

LIU Hongjuan, LUO Ting, JIANG Yuhong, et al.Based on the genetic algorithm emergency logistics facility location model study[J].Journal of Logistics Engineering University,2010,26(3):46-50.

[8]张伟．基于多目标的应急物资储备库选址决策研究[D]．重庆：重庆邮电大学，2013．

[9]花翠．城市重大灾害事故的应急物流储备库选址模型研究[D]．天津：天津理工大学，2015．

[10]AN Shi, CUI Na, LI Xiaopeng, et al. Location planning for transit-based evacuation under the risk of service disruptions[J]. Transportation Research Part B-methodological, 2013, 54(54): 1-16.

[11]Li X, Ouyang Y. Reliable traffic sensor deployment under probabilistic disruptions and generalized surveillance effectiveness measures[J]. Operations Research, 2012, 60(5):1183-1198.

[12]Jalali S, Seifbarghy M, Sadeghi J, et al. Optimizing a bi-objective reliable facility location problem with adapted stochastic measures using tuned-parameter multi-objective algorithms[J]. Knowledge-Based Systems, 2015, In Press(C):45-57.

[13]陶莎，胡志华．需求与物流网络不确定下的应急救援选址问题[J]．计算机应用，2012，32(9)：2534-2537．

TAO Sha, HU Zhihua.Facility location in emergency relief with uncertain demand and logistics network[J].Computer Application,2012,32(9):2534-2537.

[14]朱建明. 损毁情景下应急设施选址的多目标决策方法[J]. 系统工程理论与实践, 2015, 35(3):720-727.

ZHU Jianming. Methods of multi-objective decision-making for emergency facility location problem under failure scenario[J].System Engineering Theory and Practice,2015,35(3):720-727.

[15]付德强，陈煜舟，万晓榆．自然灾害风险下区域应急储备设施选址可靠性研究[J]．运筹与管理，2015，24(3)：14-19．

FU Deqiang, CHEN Yuzhou, WAN Xiaoyu. The study on the reliable model for the regional emergency storage facility under the risk of natural disaster[J].Operations Research and Management Science,2015,24(3):14-19.

[16]DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. Evolutionary Computation, IEEE Transactions on, 2002, 6(2): 182-197.