基于证据理论的地铁火灾安全评价方法*
马 剑,叶 新,林 鹏
(1.西南交通大学 交通运输与物流学院 综合交通智能化国家地方联合工程实验室,四川 成都 610031;2.西南交通大学 地球与环境科学学院 高速铁路运营安全空间信息技术国家地方联合工程实验室,四川 成都 610031)
0 引言
随着我国城市化进程的加快,交通拥堵、环境污染等问题给地面交通带来了前所未有的挑战。与地面城市交通工具相比,地铁具有速度快、污染少、能耗少、占地省、安全环保等优点[1],且能够满足大规模人群快速便捷出行的需要,因此分担了越来越多的日常公交出行比例。
虽然地铁带来许多便利,但是地铁从建设到运营过程中,特别是地铁客流高峰期,站内人员密度大,一旦出现火灾等事故,易造成群死群伤的严重后果,带来重大的经济损失[2]。例如: 1995年韩国大邱地铁站在扩建施工时,因操作失误导致煤气管道发生爆炸,造成101死亡,143人受伤[3];1995年阿塞拜疆地铁由于电动机车的电气故障引起火灾,共造成558人死亡、269人受伤,调查结果显示死亡乘客中大多是因窒息而死[4];2003年韩国大邱地铁站发生的人为纵火事件,造成极其惨烈的后果,共造成198人死亡和146人受伤,289人失踪[5];2010年俄罗斯莫斯科地铁站发生人为制造爆炸案,造成41人死亡、上百人受伤。大量的事故统计资料表明,地铁火灾安全问题需要持续重视。
为改进地铁火灾安全性,识别、发现、评价和有效管理潜在的危险源具有重要意义。因此,研究人员提出多种定性和定量的分析评价方法,例如:安全检查表、危险与可操作性、事故树、事件树、层次分析法等[6-8]。杜宝玲对大量的国外地铁事故进行统计分析,提出在地铁火灾预防上应加强可燃物控制,完善消防设施,建立救援预案[9];安永林等人利用多级可拓评价方法,对地铁火灾风险进行评估[10],此方法不用考虑一般评价中所需的隶属度函数,能对地铁火灾风险等级进行有效地评估,并可根据评价结果对风险管控中的薄弱环节提出改善意见;邓艳丽等人通过对近年来地铁火灾事故的统计分析,总结主要的起火原因,包括:电气设备故障、地铁施工引起的电火花、乘客所携带的易燃易爆物品、人为纵火[11],也提出相应的防护对策;睢羽等人着眼于地铁火灾可引起的二次事故风险,采用聚类思想,对二次事故风险进行动态综合评估,并对风险进行聚类区划,提高安全评价结果的精确性[12]。
在大多数定量安全评价中,都会涉及影响因子的量化评价,评价指标的数值分数常采用专家打分的方法。然而,专家打分往往与专家自身经历和经验有直接关系,显示出较强的不确定性。引入D-S证据理论,将不确定结果进行可靠的数值转换,融合多个证据,从而可靠评价地铁火灾安全问题。
1 D-S证据理论
1.1 基本原理
D-S证据理论是贝叶斯概率的推广,能够以不确定性信息为基础进行可信度推理。1967年,Dempster在研究不确定概率问题时,提出用多值映射思想确定概率的上、下界。1976年,他的学生Shafer用信任度函数重新表达概率上、下界,在此基础上形成“证据理论”[13]。D-S证据理论中,证据融合规则可将有一定冲突或不一致的证据进行融合,经过处理后的证据更加可靠。该方法已经成功应用于:机动车评价分析、海军系统安全分析与综合、软件系统安全性能分析、作业人员安全行为评价等方面[14-17]。在地铁安全评价中,很多评价因素同样具有不确定和模糊性,因此,对这类因素,不同专家给出的评价结果可能偏差较大。在这种情况下,将地铁火灾安全性高低作为评价目标,将专家对每一种可能导致火灾发生因素的衡量作为证据,融合不同因素的评价结果,得到其上、下界和融合后的评价结果,最终精确评价地铁火灾安全性。
1.2 评价信息的表达
在证据理论中,评价中的证据可用1个有限集合θ= {A1,A2, … ,An},其中θ非空,称θ为评价的识别框架[18]。给定识别框架θ,则函数M:2θ→[0,1]在满足M(Φ)=0,∑A⊆θM(A)=1时,称M(A)为基本概率赋值,其中2θ为θ的幂集。
对给定的M,对任意A∈2θ定义相应的信任函数和似然函数见式(1)、式(2):
Bel(A)=∑B⊆AM(B)
(1)
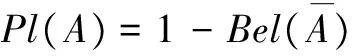
(2)
式中:信任函数Bel(A)为对A的总信任,是支持A的最小值;似然函数Pl(A)为不否定A的信任度,是支持A的最大值。这样[Bel(A),Pl(A)]就自然形成对A的信任区间。而Pl(A)-Bel(A)则用来表示不知道A的程度。
1.3 评价结果的信息融合
在安全评价过程中[19-20],由于大多数评价因素的评价指标不唯一,具有随机性,会导致评价结果有差异[21]。采用证据融合的处理方法,将同一因素的不同评价结果进行正交和运算。
设M1和M2是2个基本概率赋值,则其正交和M=M1⊕M2,见式(3)~式(5):
M(Φ)=0
(3)
M(A)=K-1×∑X∩Y=AM1(X)×M2(Y)
(4)
K=1-∑X∩Y=ΦM1(X)×M2(Y)
=∑X∩Y≠ΦM1(X)×M2(Y)
(5)
如果K≠0,则正交和M也是1个基本概率赋值,就是对M1和M2的融合;如果K=0,则不存在正交和,说明M1(X)和M2(X)矛盾。
设M1,M2,M3,…,Mn是有限n个基本概率赋值,则其正交和M=M1⊕M2⊕…⊕Mn,见式(6)~式(7):
M(A)=
K-1×∑A1∩A2∩…∩An=AM1(A1)·M2(A2)…Mn(An)
(6)
K=1-∑A1∩A2∩…∩An=ΦM1(A1)…Mn(An)
=∑A1∩A2∩…∩An≠ΦM1(A1)…Mn(An)
(7)
2 基于证据理论的地铁火灾安全评价步骤
地铁火灾安全受到建筑物内可燃物分布、人员逃生技能、消防设施设备等因素影响。为评价地铁火灾安全性,首先构建地铁火灾安全评价指标体系,根据历史数据确定每种因素的权重,接着对每种因素采用专家打分法获得证据,其次确定指标的综合概率值,最后对评分证据进行处理和分析。具体来讲,基于证据理论的地铁火灾安全评价可通过如下步骤完成:
1)建立地铁火灾安全评价指标体系。通过查阅地铁建筑相关资料,确定场所下可能出现的火灾危险源,从“人、机、管、环”4大方面分类总结,尽可能的完善指标内的各个因素。
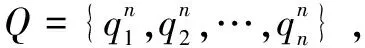
3)评价因素安全概率赋值。专家组成员对评价因素进行打分,分值上下界分别为0和1。分值越趋近于0,表示该评价因素越危险,用这种打分方式避免在不确定性问题上的只用“是否”来简单判断。专家组成员对指标体系内的评价因素进行打分,分值越靠近1,表示越安全。
4)指标综合概率值的确定。根据每个评价因素所在层次,评价因素的概率值为评价安全概率值乘上对应总目标的各级权重qn。以3层权重指标的第1个因素θ111为例:
(8)
其中n为因素在体系中的等级数,n=1,2,3。最终获得综合概率值集合M{M{θ111},M{θ112},…,M{θrst}},以及与其对应的不确定性值m{θ}=1-M{θ111}-M{θ112}-…-M{θrst},其中m{θ}是评价因素的概率值的补集,表达对应的不确定性,r=1,2,3…;s=1,2,3…;t=1,2,3…。
5)综合评价。根据上面因素的综合概率值的确定,利用式(1)和式(2)可以求得各大类指标的信任函数上、下界。如果有多个专家评价结果,可利用式(3)~式(7),对多组评价结果整合,使最终评价结果更加精确、真实。
3 基于证据理论的地铁火灾安全评价与分析
3.1 地铁火灾安全评价指标体系的建立
因为地铁建筑的特殊性,其潜在的危险源与常规建筑物不同,发生火灾后消防设施设备的使用不同,管理制度和应急预案也有不同。此外,由于地铁内部的结构限制,人员可视范围有限,对人员在紧急情况下的逃生有一定的限制。所以研究地铁火灾问题时,要综合考虑多个方面的因素,如:从“人”的方面,应该考虑地铁内部的人员组成,再确定人的消防意识、应急能力等;从“设备”的方面,应该考虑站内设备是否能正常工作,消防系统是否能最大化运用;从“环境”的方面,应该考虑地铁站内火灾荷载的大小,如果地铁站为多种交通方式的枢纽站,乘客携带行李会比其他站多,可燃物的数量和种类增多,都会给地铁火灾的预防带来更大的挑战;从“管理”的方面,应考虑消防管理制度是否合理,消防教育训练等是否到位。
通过查阅相关文献资料[22-23],结合地铁建筑特点,建立地铁火灾安全评价指标体系,并根据历史数据确定指标中的各因素权重。建立的地铁火灾安全评价指标体系,如表1所示。表中θijk表示评价指标的各级因素,i,j,k表示第1,2,3级因素,括号内数字为该级指标的权重。

表1 地铁火灾安全评价指标体系及权重
3.2 初级评价
3.2.1评价初始数据
根据表1中的地铁火灾安全评价指标体系,评价因素集合θ=﹛θ111,θ112,θ121,θ122,θ123,θ211,θ212,θ213,θ221,θ222,θ223,θ231,θ232,θ233,θ311,θ312,θ313,θ314,θ321,θ322,θ323,θ41,θ42,θ43,θ44﹜。专家组成员对指标体系内的评价因素进行打分,分值越靠近0,表示评价项目的安全状态越危险或项目的安全工作能力越低,导致地铁火灾发生的可能性越大。地铁火灾安全评价结果分类指标,如表2所示。

表2 地铁火灾安全评价结果分类
3.2.2指标综合概率值
根据每个评价因素所在层次,评价因素的概率值为评价分值乘上对应总目标的综合权重q。以因素“乘客的消防意识性等级”为例,已知因素“乘客的消防意识性等级”评分值为b,则因素“乘客的消防意识性等级”的综合概率值为:
M{θ111}=b×q1×q2×q3
(9)
由此可得综合概率值集合M{M{θ111},M{θ112},…,M{θ44}},以及其对应的不确定性值m{θ}=1-M{θ111}-M{θ112}-…-M{θ44}。
3.3 评价分析
根据表1中的地铁火灾安全评价指标体系,对某地铁站进行地铁火灾安全评价。专家组成员对评价因素进行打分,分值越靠近0,表示越不能保证安全状态。表3为采用同一评价指标体系,不同专家打分结果汇总。
利用综合概率值计算可得第1组评分的综合概率值集合M{M{θ111},M{θ112}, …,M{θ44}},m{θ}} ={0.016 9, 0.039 4, 0.008 3, 0.022 0, 0.048 1, 0.016 0, 0.022 2, 0.030 1, 0.004 8, 0.024 0, 0.010 5, 0.007 9, 0.002 3, 0.007 9, 0.028 7, 0.023 6, 0.042 8, 0.009 5, 0.005 6, 0.020 5, 0.031 1, 0.010 0, 0.015 0, 0.022 5, 0.052 5, 0.478 0}。
在此基础上,利用式(1)可得起火因素的信任函数:
Bel(θ1)=M{θ111}+M{θ112}+M{θ121}+
M{θ122}+M{θ123}=0.134 6
(10)
类似地,有Bel(θ2)=0.125 6,Bel(θ3)=0.161 7,Bel(θ4)=0.100 0。
利用式(2)可得人的因素的似然函数:
1-(M{θ21}+M{θ221}+…+M{θ44})=0.612 7
(11)
类似的,有Pl(θ2)=0.603 6,Pl(θ3)=0.639 8,Pl(θ4)=0.578 0。

表3 地铁火灾安全检查
可见由人的因素θ1引发的不安全评价的赋值下界是0.134 6,上界为0.612 7。对于不确定性问题,与利用其它评价方法相比,运用证据理论可将其不确定性概率的范围确定,从而便于对该问题的进一步量化分析。
3.4 证据融合
证据融合是证据理论优势的最重要体现,特别是当不同的专家给出的评价结果有差异时,依据证据理论,依然可以得到可靠的评价结果。为说明这一特性,假设针对某地铁站,依据前文建立的评价体系,共有7位专家参与评价,每位专家给出的评分详见表3。
为便于比较,假设专家6与专家5除对“乘客的消防意识性等级”一项打分略有区别外,其余各项评分均相同。进一步假定专家7与专家6对“消防常规检查”一项的评定有异议,但其余各项指标打分均一致。专家5,专家6和专家7给出的评议,定性上显示其对该地铁站的安全性逐次提高。
依据证据融合理论进行证据融合,结果如下:M1{{θ1},{θ2},{θ3},{θ4},θ}={0.135,0.126,0.162,0.100,0.478};M2{{θ1},{θ2},{θ3},{θ4},θ}={0.150,0.130,0.154,0.105,0.461};M3{{θ1},{θ2},{θ3},{θ4},θ}={0.156,0.138,0.166,0.095,0.445};M4{{θ1},{θ2},{θ3},{θ4},θ}={0.168,0.118,0.170,0.113,0.432};M5{{θ1},{θ2},{θ3},{θ4},θ}={0.055,0.064,0.070,0.062,0.748};M6{{θ1},{θ2},{θ3},{θ4},θ}={0.061,0.064,0.070,0.062,0.743};M7{{θ1},{θ2},{θ3},{θ4},θ}={0.061,0.064,0.070,0.108,0.700}。
根据式(3)~式(7)正交和运算:
类似有M1,2({θ2})=0.173,M1,2({θ3})=0.219,M1,2({θ4})=0.135。则:
m(θ)=1-∑iθi=1-(0.291+0.235+0.031+0.107)=0.278
整理可得:M1,2{{θ1},{θ2},{θ3},{θ4},θ}={0.195,0.173,0.219,0.135,0.278}
再将以上结果与剩下的专家评分结果逐个融合,最后得到:
M123{{θ1},{θ2},{θ3},{θ4},θ}={0.229,0.198,0.256,0.141,0.175};M1234{{θ1},{θ2},{θ3},{θ4},θ}= {0.255,0.199,0.282,0.149,0.115}。
至此,可以发现1到4号专家评分结果分别为“亚安全”级别,通过逐个融合后,将不确定的区间逐步缩小,4次评分结果融合后的结果为Bel({θ1,θ2,θ3,θ4})=0.885,Pl({θ1,θ2,θ3,θ4})=1,信任区间为[0.885,1],不确定度为0.115,因此综合评定结果为“安全”级别。
为说明证据融合理论的优点,我们考虑将前述7位专家评分结果分为3组:
1)第1到4号专家与5号专家的评分结果结合作为第1组;
2)第1到4号专家与6号专家的评分结果结合作为第2组;
3)第1到4号专家与7号专家的评分结果结合作为第3组。
分别进行证据融合,则有:
M12345{{θ1},{θ2},{θ3},{θ4},θ}={0.253,0.039,0.286,0.153,0.268};M12346{{θ1},{θ2},{θ3},{θ4},θ}= {0.256,0.040,0.286,0.153,0.265};M12347{{θ1},{θ2},{θ3},{θ4},θ}={0.252,0.041,0.283,0.167,0.257}。
由于专家5给出的评分结果与前4位专家有较大的差异,该专家的打分显示某地铁站的综合评价为“危险”,因此,第1组评分的融合结果为Bel({θ1,θ2,θ3,θ4})=0.732,Pl({θ1,θ2,θ3,θ4})=1,信任区间为[0.732,1],不确定度为0.268,综合评价显示为“亚安全”级别,与前4位专家打分融合相比,这一综合结果的不确定性显著增加。
专家6的评分与专家5相比,评价指标内的第1个3级评价指标“乘客的消防意识性等级”有微小的不同,因此,将专家6的评分与前4位专家的评分进行融合得到第2组评分的融合结果为Bel({θ1,θ2,θ3,θ4})=0.735,Pl({θ1,θ2,θ3,θ4})=1,信任区间为[0.735,1],不确定度为0.265,综合评价显示为“亚安全”级别。该结果与第1组评分融合结果一致,但是信任函数与第1组评分的融合结果相比增大了0.003,这是因为专家6对该地铁站的安全水平打分略高于专家5,该专家的打分更倾向于接近前4位专家打分。
专家7的评分与专家6相比,最后1个2级评价指标“消防常规检查”有较大的差别。在该方面,专家7认为该地铁系统安全性较好。因此,第3组评分的融合结果为Bel({θ1,θ2,θ3,θ4})=0.743,Pl({θ1,θ2,θ3,θ4})=1,信任区间为[0.743,1],不确定度为0.257,综合评价显示为“亚安全”级别。与第2组结果相比,虽然评价结果也显示为“亚安全”级别,但是该结果的信任函数相比增大了0.008,不确定性有所降低。这是由于虽然专家7对该地铁站的整体评价与前4位专家有较大差异,但是在最后1个2级评价指标上,与专家6相比,专家7的打分与前4位专家打分更一致,因此,专家7给出的评价的可信度更高,将其打分与前4位专家的打分相融合就更可靠。进一步与前4位专家的综合评价结果相比,由于专家7在其他各项打分上存在较大差异,因此,该组结果的不确定度显著增加,从而使得综合评价结果变为“亚安全”级别。
通过对以上3组评分融合处理结果的分析可以发现,证据理论可以有效融合证据(也即评分)中的一致部分,从而将数据的中的不确定性值的范围减小,使评价结果更加的精确可靠;在有数据冲突或较为不一致时,该方法也综合考虑各证据之间的共同部分,进行合理的融合,避免因人的判断误差而对最终结果产生影响。
4 结论
1)由于地铁建筑结构与功能特殊性,建立由人的因素、设备因素、管理因素和环境因素4大方面组成的地铁火灾安全评价指标体系,并通过调研相关资料,对其中的各级因素分配权重,考虑各级因素在整个体系中的重要性,提出综合概率值。
2)运用D-S证据理论,通过初级处理后,评价数据得到数学量化,使评价结果更加精确。进而将多组评价结果进行再处理,得到不确定性问题的赋值上界和下界。最后利用证据融合法则,综合考虑多组评价结果,有效减少因人的判断偏差而引起的随机误差,使评价结果更加全面可信。
3)对某地铁火灾安全评价结果显示,对于一致的评价结果,证据理论的融合法则有效的将不确定范围减小;对于有一定冲突的检查结果,通过融合法则处理,最终结果能综合考虑到每个评价依据。案例表明,环境的不确定因素对整个体系影响较大,在地铁火灾的应急管理中,应对环境因素加强管理。
[1]杨立中, 邹兰. 地铁火灾研究综述[J]. 工程建设与设计, 2005(11): 8-12.
YANG Lizhong, ZOU Lan. Review on tunnel and subway fire researches [J]. Construction & Design for Project, 2005(11): 8-12.
[2]ESKESEN S D, TENGBORG P, KAMPMANN J, et al. Guidelines for tunnelling risk management: International Tunnelling Association, Working Group No.2[J]. Tunnelling and Underground Space Technology, 2004, 19(3): 217-237.
[3]徐宝康.特写:大邱地铁纵火惨案震惊韩国[EB/OL]. http://www.people.com.cn/GB/guoji/22/82/20030218/925683.html,2003-02-18.
[4]中国网. 1995年10月28日 阿塞拜疆巴库地铁失火死伤惨重[EB/OL].http://www.china.com.cn/aboutchina/txt/2009-10/26/content_18770645.htm,2009-10-26.
[5]百度.韩国大邱地铁纵火案[EB/OL].http://baike.baidu.com/ link?url=_cjUIjJ2hGxbBtozGzhi1OU9xiYcXkcwHp9jAi6kQzNIjW LFkciVGmEHNeei99jHnhPQHLQCnpDneyAaWconiK,2017-01- 11.
[6]游鹏飞,牟瑞芳.地铁土压平衡式盾构隧道施工安全评价模式研究[J].岩石力学与工程学报,2010,29(z1):2663-2668.
YOU Pengfei, MU Ruifang. Safety assessment model of metro epb shield tunnel construction[J]. Chinese Journal of Rock Mechanics and Engineering, 2010,29(z1):2663-2668.
[7]卢亿.地铁火灾的事故树分析[J].城市轨道交通研究,2011,14(2):95-97, 102.
LU Yi, Fault tree analysis of fire disaster in subway [J].Urban Mass Transit, 2011,14(2):95-97,102.
[8]鲍学英,王起才,宫文昌.基于模糊层次分析法的地铁工程施工安全评价[J].中国安全生产科学技术,2013,9(1):136-139.
BAO Xueying, WANG Qicai,GONG Wenchang. Study on safety assessments of metro constructions using fuzzy analytic hierarchy process [J]. Journal of Safety Science and Technology, 2013,9( 1):136-139.
[9]杜宝玲.国外地铁火灾事故案例统计分析[J].消防科学与技术,2007,26(2):214-217.
DU Baoling. Statistic analysis of the foreign underground fire accidents cases [J]. Fire Science and Technology, 2007, 26(2): 214-217.
[10]安永林,彭立敏.地铁火灾风险性的多级可拓综合评估[J].防灾减灾工程学报,2009,29(5):566-571.
AN Yonglin, PENG Limin.Multi-level extensible assessment of subway fire risks [J]. Journal of Disaster Prevention and Mitigation Engineering, 2009,29(5):566-571.
[11]邓艳丽,谭志光.地铁火灾研究现状综述[J].安防科技,2008(1):6-8.
DENG Yanli, TAN Zhiguang.Reviewed subway fire research [J]. Security and Safety Technology Magazine, 2008(1):6-8.
[12]睢羽,宋守信.基于投影寻踪聚类思想的地铁火灾二次事故风险评估[J].消防科学与技术,2013,32(7):789-793.
SUI Yu, SONG Shouxin. Secondary accident risk caused by subway fire based on projection pursuit clustering method [J]. Fire Science and Technology, 2013, 32(7):789-793.
[13]梅莹,丁晓明.证据理论在软件需求工程中的应用研究[J].计算机科学,2012,39(s3):237-239.
MEI Ying,DING Xiaoming.Study on the application of evidence theory in software requirements engineering [J]. Computer Science, 2012, 39(s3):237-239.
[14]李珂,杨杨,邱雪松. 城市汽车导航中一种改进的D-S证据理论地图匹配算法[J]. 测绘学报,2014,43(2):208-213,220.
LI Ke, YANG Yang, QIU Xuesong. An improved map matching algorithm based on D-S evidence theory in city vehicle navigation [J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(2):208-213,220.
[15]孙越林,包磊.基于D-S证据理论的海战场目标战术意图识别技术研究[J].舰船电子工程,2012,32(5):48-51.
SUN Yuelin, BAO Lei. Study on recognition technique of targets’ tactical intentions in sea battlefield based on D-S evidence theory [J]. Ship Electronic Engineering, 2012, 32(5):48-51.
[16]鞠彦兵,冯允成,姚李刚.基于证据理论的软件开发风险评估方法[J].系统工程理论方法应用,2003,12(3):218-223.
JU Yanbing, FENG Yuncheng, YAO Ligang. Research on the measure of risk in the course of software development [J]. Systems Engineering-Theory Methodology Application, 2003, 12(3):218-223.
[17]郑霞忠,石法起,陈述,等.基于D-S证据理论的地下洞室作业人员安全行为评价[J].中国安全生产科学技术,2016,12(6):158-162.
ZHENG Xiazhong, SHI Faqi, CHEN Shu, et al. Evaluation on safety behavior of workers in underground cavern based on D-S evidence theory [J]. Journal of Safety Science and Technology, 2016, 12(6):158-162.
[18]SHAFER G. A Mathematical theory of evidence [M]. Princeton University Press, 1976.
[19]段新生.证据理论与决策,人工智能[M].北京:中国人民大学出版社,1993.
[20]王雪荣.一种基于证据理论的动态综合效绩评价实用方法[J].中国管理科学,2006,14(4):121-127.
WANG Xuerong. The practical method of dynamically evaluating the comprehensive performance based on evidential reasoning [J]. Chinese Journal of Management Science, 2006, 14(4): 121 -127.
[21]王晨.D-S证据理论在商场火灾安全评价中的应用[J].消防科学与技术,2010,29(4):335-338.
WANG Chen. Application of D-S evidence theory in shopping center fire safety assessment [J]. Security and Safety Technology Magazine, 2010, 29(4):335-338.
[22]李炎锋,石勃伟,王超,等.城市地下轨道交通火灾风险评估体系模型研究——以某地铁车站为例[J].防灾减灾工程学报,2010,30(6):680-684.
LI Yanfeng, SHI Bowei, WANG Chao, et al. Study on fire risk assessment system urban underground rail traffic: a subway station is selected as example [J]. Journal of Disaster Prevention and Mitigation Engineering, 2010, 30(6):680-684.
[23]史聪灵,钟茂华,何理,等.地铁车站及隧道全尺寸火灾实验研究(1)-实验设计[J].中国安全生产科学技术,2012,8(6):22-28.
SHI Congling, ZHONG Maohua, HE Li, et al. Investigation of full-scale fire experiments in metro station and tunnel (1)—experimental setup [J]. Journal of Safety Science and Technology, 2012,8(6):22-28.

