基于RANSAC的鸡蛋凹陷检测
杨 群,敖天镇
(广东工业大学 信息工程学院,广东 广州 510006)
基于RANSAC的鸡蛋凹陷检测
杨 群,敖天镇
(广东工业大学 信息工程学院,广东 广州 510006)
现代化的蛋品加工业中,传统的照蛋检测鲜有鸡蛋凹陷缺陷检测。为了实现快速在线检测,提出一种基于RANSAC的鸡蛋凹陷检测系统设计方案。在工业生产线上,将鸡蛋图片进行灰度转化、阈值分割、最小外接矩形法、角点检测,最后用多模RANSAC算法拟合蛋形曲线。通过对拟合蛋形曲线和鸡蛋壳曲线的比较,判断是否为凹陷鸡蛋,该算法的多模平均拟合时间为每个0.45s,检测精度达到91%,证明算法具有较强的鲁棒性和实时性。
蛋形曲线;RANSAC拟合;阈值分割;角点检测
0 引言
基于机器视觉的鸡蛋凹陷缺陷检测,是图像处理技术在农业生产上的应用。鸡蛋凹陷缺陷检测的主要问题和难点是确定鸡蛋长径以及多个鸡蛋蛋形曲线拟合。很多专家学者对鸡蛋方面的研究主要集中在鸡蛋裂纹、脏斑、蛋形指数等方面,而对鸡蛋外壳曲线鲜有研究,鸡蛋外壳曲线能够直接判断鸡蛋是否存在凹陷。国内外检测曲线主要集中在圆和椭圆两个方面。李寒等[1]采用局部极大值法和随机圆环变换检测圆算法实现单个番茄、多个番茄目标提取,但是算法的实际应用性、可靠性需进一步提高。袁理等[2]根据椭圆极和极弦的性质,随机采样2点,验证第3点是否在椭圆上,算法的缺陷是对颗粒噪声没有抵抗能力。A·Goneid[3]基于hough变化的一维累加器数组来检测二值图像中的圆环和椭圆,该方法的缺陷是图像中不能有颗粒噪声。Tomonari Masuzaki[4]等假设所采集图像的点是空间连接的,选取内点拟合椭圆,然后计算误差,该方法的缺陷是不能进行多模拟合。
为了解决一副图像中有多个鸡蛋,并且存在因曝光和鸡蛋表面钙化物质不均匀产生的颗粒噪声问题,提出外接矩形法对鸡蛋进行目标提取。该方法首先对鸡蛋图像灰度化后的图像进行最大类间分割,检测获取角点,然后采用外接矩形法统计鸡蛋个数,最后使用RANSAC算法拟合蛋形曲线。该算法避免了因颗粒噪声对鸡蛋壳曲线拟合的影响,同时也解决了多模拟合蛋形曲线的问题。
1 基于RANSAC的鸡蛋检测
1.1 蛋形曲线检测原理
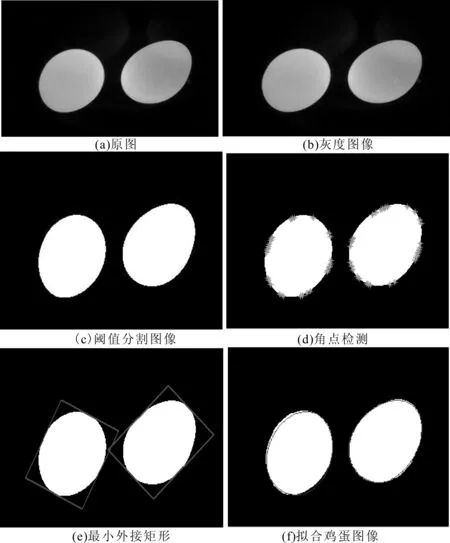
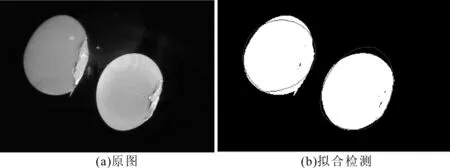
蛋形曲线的方程为:x4+2dx2y2+fy4=ax3+cxy2+ey2(1),相对于蛋形曲线方程{(cx)2+y2}2=a(cx)3+(a-b)cxy2,该曲线方程函数中参数的次数为一次,方程方便确定参数并且简便运算。经过数学推导和大量的实验数据证明,满足条件a<0,d>0,f>0,-3000 2a2d≥ac+e,0.44 1.2 角点检测 本文采用最大类间方差法[5]分割图片,自动计算出最优阈值,将图像分成两个区域(0代表暗区域,1代表亮区域),避免角点检测时,因图片曝光和鸡蛋表面钙化位置分布不均匀问题,而误产生兴趣点。相较于选用全部的边缘点运算,选用角点具有如下优点:检测出的角点数量集数量少,抽取适合角点耗费时间短,并且检测具有稳定性。 1.3 蛋形曲线方向确定 对最大类间方差法的二值图像,采用4连通域[6],连通域面积小于50的区域删除,能够将曝光不均匀的区域删除。然后用最小矩形面积法[7]获取每个鸡蛋的最小外接矩形,在MATLAB中用函数[rx,ry,area]=minboundrect(x,y)表示。矩形4个端点的坐标逆时针顺序分别为l1(x1,y1)、l2(x2,y2)、l3(x3,y3)、l4(x4,y4)。分别计算出过点l1和点l2,点l2和点l3,点l3和点l4,点l4和点l1的4条直线方程,直线和图像边缘坐标的交点,即为鸡蛋轮廓的端点坐标。其中数组boundary为鸡蛋轮廓坐标,解出的端点坐标不止一个值,取其中点值。遍历数组中的4个点,计算出距离最长的两个点,即为鸡蛋长径端点坐标,另外两点即为短径端点坐标。设长径端点为(m1,n1),(m2,n2),短径端点(m3,n3),(m4,n4),,则长径中点坐标为x01=(m1+m2)/2,y01=(n1+n2)/2,旋转角度为θ=arctan((n2-n1)/(m2-m1)),即长径直线于水平方向的夹角。 图1 蛋形曲线 Step1:将采集的彩色图像进行灰度转换[8]如图2(b)所示,进行最大类间分割得到图像如图2(c)所示。二值图像I1采用4连通域,连通域面积小于50的区域删除。运用最小矩形法获取每个鸡蛋的最小外接矩形,自动统计图片中鸡蛋数目如图2(d)所示,将每个鸡蛋的轮廓坐标保存在数组boundary中,并且统计每个鸡蛋边缘点数为p。对二值图像进行角点检测,获取角点坐标,存储在数组mdata中。设置蛋形曲线条件存放数组II,存放每个满足蛋形曲线点数数组M。 Step2:初始化数组M和II,按标记鸡蛋数目连通域顺序获取最小外接矩形端点的坐标l1(x1,y1)、l2(x2,y2)、l3(x3,y3)、l4(x4,y4)。遍历计算出l1、l2、l3、l4欧氏距离最长的两点,分别计算出过点l1和点l2、点l2和点l3、点l3和点l4、点l4和点l1的4条直线方程直线和图像边缘坐标的交点,交点坐标不止一个,取值中间一点,为鸡蛋轮廓的端点坐标,存放在数组point中。遍历数组中的4个点,计算出距离最长的两个点,即为鸡蛋长径端点坐标,距离为pisto,另外两点即为短径端点坐标。设长径端点为(m1,n1),(m2,n2),短径端点为(m3,n3),(m4,n4),则长径中点坐标为x01=(m1+m2)/2,y01=(n1+n2)/2,旋转角度为θ=arctan((n2-n1)/(m2-m1)),θ2=-θ,距离pisto=((n1-n2)2+(m1-m2)2)1/2。 Step3:对鸡蛋轮廓坐标、角点坐标、长径短径端点整体平移(-(x01+x02)/2,-(y01+y02)/2),旋转矩阵为[cosθ,-sinθ;sinθ,cosθ],再次平移为(pisto/2,0),可得到长径水平放置,端点在原点,且经过(pist0,0)点的蛋形,短径两端点在蛋形竖直方向上。设置鸡蛋计数器ncount,最大计数值为N,循环计数器ncount1,最大计数值为N1,点数计数器ncount2,初始化ncount,ncount1,ncount2的值。平移旋转后长径,短径两端点的坐标,删除其中的坐标(0,0),获得3个定点。 Step4:选定3个定点,再从所有角点中任取2点。如果满足蛋形曲线条件,则进行下一步,否则重新选点至符合为止。 Step5:将拟合的蛋形曲线值与鸡蛋轮廓的纵坐标值比较,若相差阈值小于T,则ncount2加1,循环统计ncount2的值,存放在数组M中,蛋形曲线条件存放在数组II中,ncount1值加1。若ncount1小于N1,则返回Step4。否则,进行下一步。 Step6:找出数组M中点数最大值为MM,点数符合率G=MM/p,对应数组II中对应的蛋形曲线条件,拟合蛋形曲线,将拟合的蛋形曲线平移(-pisto/2,0),旋转矩阵为[cosθ2,-sinθ2;sinθ2,cosθ2],平移((x01+x02)/2,(y01+y02)/2),得到实际蛋形跟拟合蛋形的比较结果。ncount的值会自加1,然后与N比较,若小于N,返回Step2继续循环拟合蛋形曲线;若不小于N,则进行下一步。 Step7:程序结束。 本实验选用250张图片进行测试。算法能够自动统计鸡蛋个数,克服颗粒噪声的影响,具有鲁棒性和实时性,能够进行多模拟合,图片中有两个鸡蛋时,平均拟合的时间为每个0.45s左右。图2为多模RANSAC[9]曲线拟合算法处理结果。多模RANSAC拟合蛋形算法都具有鲁棒性。任意两个角度,拟合出多模蛋形曲线如图3所示。 通过检测200张完整鸡蛋图片和200张破损鸡蛋图片,设定阈值差T为15,符合率G大于95%时,为完好鸡蛋;低于95%时,为破损鸡蛋。对破损的鸡蛋运用该RANSAC算法,图4为单模破损鸡蛋检测图像,图5为多模破损鸡蛋检测图像。 在蛋品加工生产线上,用矩形外接算法和RANSAC拟合蛋形曲线算法能够有效地提取单蛋、多蛋的鸡蛋目标,通过拟合曲线和实际蛋形曲线比较,能够判断鸡蛋是否存在凹陷缺陷。算法具有准确性、鲁棒性和实时性,解决了颗粒噪声对确定鸡蛋长径中心的影响,以及多目标拟合蛋形曲线的问题,多模算法的平均时间为每个0.45s,精确度能够达到91%。但由于RANSAC随机取点的重复性,该算法的时效性还有待进一步提高。 图2 多模RANSAC曲线拟合算法处理结果 图3 多模RANSAC拟合蛋形 图4 单模破损鸡蛋检测 图5 多模破损鸡蛋检测 [1] 李寒,王库,曹倩,等.基于机器视觉的番茄多目标提取与匹配[J].农业工程学报,2012,28(5):168-172. [2] 袁理,叶露,贾建禄.基于Hough变换的椭圆检测算法[J].中国光学,2010,3(4):379-384. [3]GONEIDA,ELGINDIS,SEWISYA.Amethodforthehoughtransformdetectionofcirclesandellipsesusinga1-dimensionalarray[C].IEEEInternationalConferenceonSystem,1997:3154-3157. [4]MASUZAKIT,SUGAYAY.Connectivity-basederrorevaluationforellipsefitting[C].IAPRInternationalConferenceonMachineVisionApplications,2015. [5] 薛景浩,章毓晋.基于最大类间后验交叉熵的阈值化分割算法[J].中国图象图形学报,1999(2):110-114. [6] 冈萨雷斯.数字图像处理的MATLAB实现[M].清华大学出版社,2013. [7] 吴晓光,王涤琼,盛慧.一种获取图像区域最小外接矩形的算法及实现[J].计算机工程,2004,30(12):124-125. [8]DAIC,RONGW,FANZ,etal.AnoveldetectionalgorithmofmicrospheresbasedonHoughtransformandellipsefitting[C].IEEEInternationalConferenceonMechatronicsandAutomation,2015. [9]MOUX,SHINBS,WANGH.HierarchicalRANSACforaccuratehorizondetection[C].MediterraneanConferenceonControlandAutomation,2016. (责任编辑:孙 娟) 杨群(1991-),男,河南信阳人,广东工业大学信息工程学院硕士研究生,研究方向为图像处理;敖天镇(1989-),男,河南信阳人,广东工业大学信息工程学院硕士研究生,研究方向为图像处理。 10.11907/rjdk.162597 TP319 A 1672-7800(2017)003-0125-03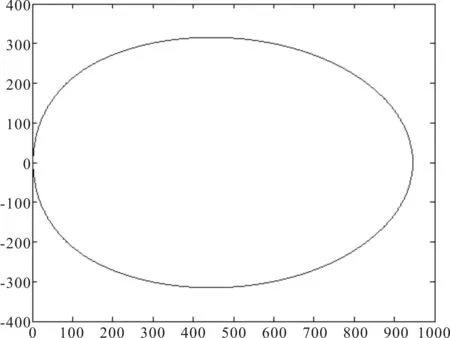
2 多模RANSAC算法步骤
3 实验结果与分析
4 结语