基于极限学习机的三维图形重构虚拟仿真实验研究

陈 龙， 郄小美， 黄信静

(杭州电子科技大学 电子信息学院， 杭州 310018)

基于极限学习机的三维图形重构虚拟仿真实验研究

陈 龙， 郄小美， 黄信静

(杭州电子科技大学 电子信息学院， 杭州 310018)

针对极限学习机容易导致过拟合、泛化能力小等局限性，采用移动加权极限学习机和正则极限学习机优化算法，平衡原始极限学习机存在的结构风险和经验风险，提高极限学习机的泛化能力；并用该算法对墨西哥帽子函数进行三维重构虚拟仿真实验。实验表明,这两种算法能够有效的降低重构误差，提高算法的泛化能力。该仿真实验可用于神经网络及Matlab虚拟仿真实验教学，对提高学生自主学习能力，编程与调试能力起到积极作用。

极限学习机； 拉格朗日乘子法； 三维图形重构； 虚拟仿真实验； 能力培养

0 引 言

近年来各高校对学生的培养已经不仅仅是局限于理论知识和课堂实验的教学，更注重对学生创新思维和创新能力的培养[1]。虚拟仿真技术是伴随着计算机技术的发展而逐步形成的一类实验研究的新技术，并在教学上取得了良好的效果；人工神经网络作为模仿生物神经网络行为特征的一种数学模型，提出之后在神经科学、人工智能和计算机科学等领域得到了广泛研究[2]。极限学习机算法在2004年由新加坡南洋理工大学黄广斌教授等[3-4]提出，是一种快速的单隐层前馈神经网络(Single-hidden Layer Feedforward Neural Network,SLFN)算法，该算法通过大量的样本计算确定神经网络的传输参数，相对于传统神经网络因迭代计算传输参数消耗大量时间，极限学习机算法计算过程无需迭代，训练速度快，泛化能力好。

传统上三维图形的重构直接通过恢复图像的深度信息或需要多幅图像来实现[5-11]，本文采用的极限学习机、移动加权极限学习机和正则极限学习机对三维图形的重构实现简单，精确度高。极限学习机仿真研究的方法可用于虚拟仿真实验教学，通过虚拟仿真实验中算法优化和软件仿真提高学生的科研能力和实践能力[12]，且此类实验在虚拟仿真实验教学中成本低，可开展规模大，为各高校对学生实践能力的培养提供了新的思路。

1 极限学习机

SLFN的模型如图1所示，包括输入层、隐藏层和输出层，其中单个隐藏层神经元的模型如图2所示，输入xi与对应权值wi相乘求和后加偏置b，经激活函数g(x)限幅得隐藏层神经元输出为

(1)

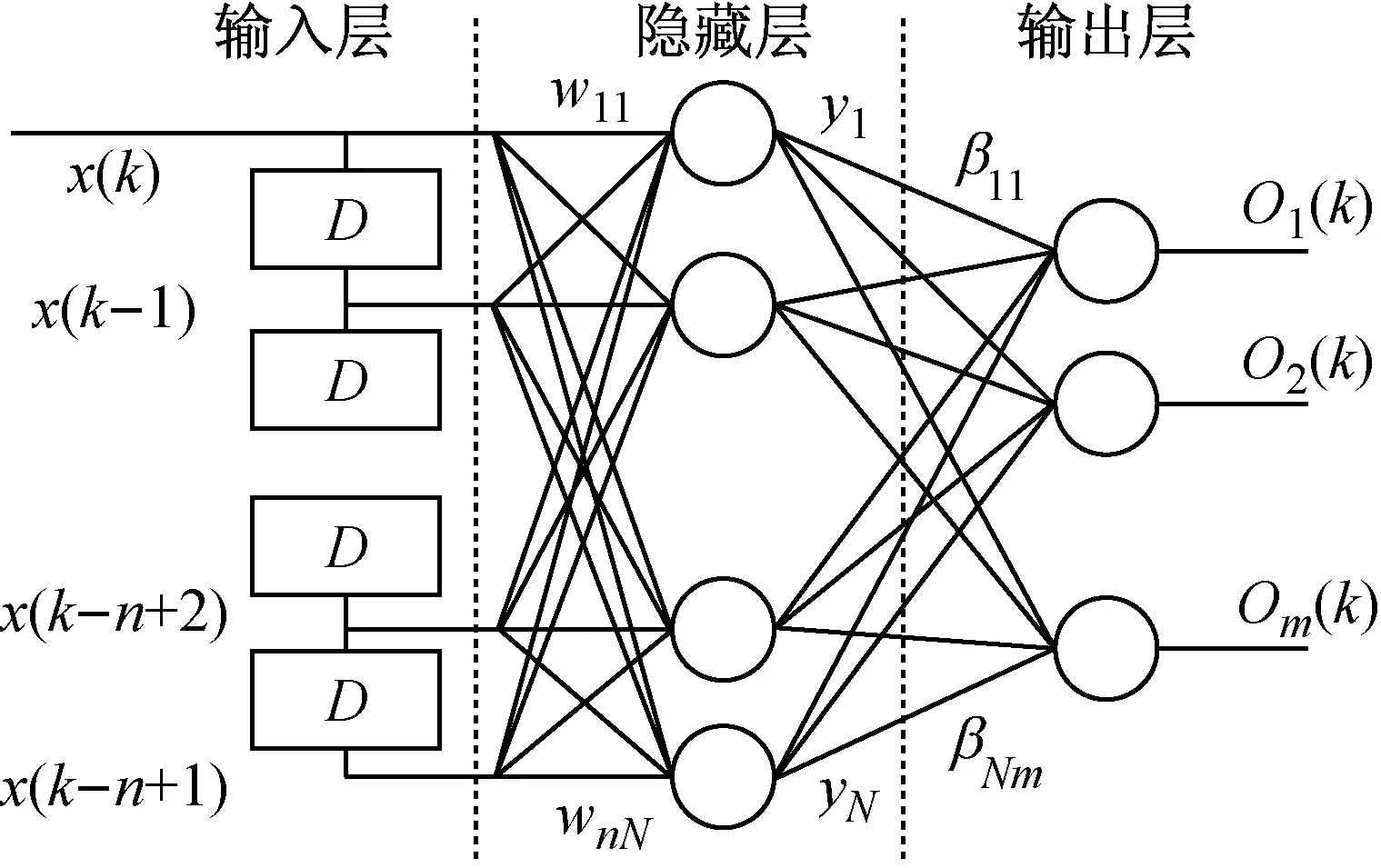
图1 单隐藏层前馈神经网络模型图

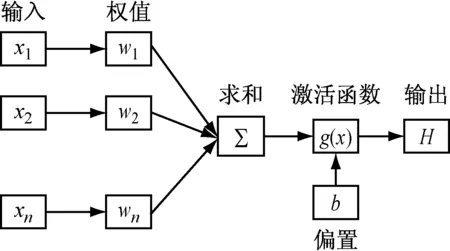
图2 单个隐藏层神经元模型图

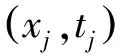
(2)

为了使模型的实际输出Oj零误差的逼近于期望输出tj，即

(3)

采用矩阵表达式，式(3)可简化为

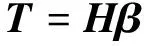
(4)

输入权值矩阵W和偏置矩阵b可随机设定[3]，根据Moore-Penrose广义逆矩阵和最小范数最小二乘解[13]的相关定理得:

(5)

H+为隐藏层输出矩阵H的Moore-Penrose广义逆。

ELM训练过程即求输出权值矩阵β的过程，ELM算法实现流程如图3所示，对于给定训练样本，首先，设定隐藏层神经元个数，随机初始化输入权值矩阵W和偏置矩阵b，选择合适的激活函数；其次，根据式(1)计算极限学习机每个隐藏层神经元的输出H，通过式(5)计算得输出权值矩阵β；最后，根据所得β对测试样本进行仿真，对仿真结果进行对比和分析，测试结果不满足要求时可通过适当增加训练样本或隐藏层神经元个数改善。

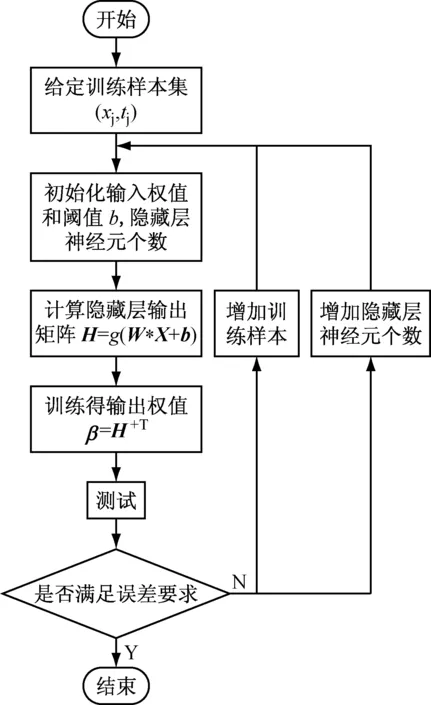
图3 ELM算法实现流程图

2 极限学习机优化设计

ELM算法基于经验风险最小化原则，未考虑结构风险，在实际应用中容易导致过度拟合的问题；ELM直接求最小二乘解，当样本数据发生改变时，无法对参数进行调整；针对ELM的这些缺点，查阅多种ELM优化设计算法，采用移动加权极限学习机和正则极限学习机进行三维图形重构虚拟仿真实验的研究。

2.1 移动加权极限学习机

移动加权极限学习机应用移动最小二乘法原理，针对不同的输入样本，根据选择的权函数训练不同样本的权重，输出权值为一个与输入有关的权函数，而不是一个固定的数值矩阵，从而提高算法的稳定性[13-14]。

移动加权极限学习机算法的数学模型为

(6)

实际输出Oj与期望输出tj之间的加权损失平方函数为

E(x)=

(7)

(8)

式中，P(x)=HTW(x)。

移动加权极限学习机训练过程中训练数据按一定的规则分类，每一类数据单独训练网络参数β(x)，用得到的网络参数β(x)对具有相似特征的数据类进行测试，避免了原始极限学习机在处理不规则数据时泛化能力差的缺点。

2.2 正则极限学习机

正则极限学习机通过参数γ来调节经验风险和结构风险的比例[15]。数学模型为

(9)

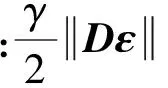
用拉格朗日方程将求式(9)的最小值转换为无条件极值求解问题，R-ELM的数学模型可用拉格朗日方程表示为

(10)

式中：α为拉格朗日乘子，根据KKT优化条件令该函数分别对β、α、ε求梯度：

(11)

根据拉格朗日方程求极值方法，解得输出权值矩阵为

(12)

当D为单位对角矩阵时，该算法称为无权正则极限学习机；否则，称为有权正则极限学习机。原始极限学习机是无权极限学习机在γ趋向于无穷大时的特殊情况。正则极限学习机提高了原始极限学习机的泛化能力，改善了原始极限学习机存在的过拟合问题。

3 基于ELM的三维图形虚拟仿真实验设计

本实验案例采用Matlab作为仿真环境，Matlab功能强大，集成度高，使用简单，在信号处理、自动控制和电子仿真等方面应用广泛，使用Matlab软件进行虚拟实验仿真已经是大学生必须掌握的一项基本技能。

(a)墨西哥帽子三维图形原图 (b)原始ELM重构结果

(c)MLS⁃ELM重构结果 (d)R⁃ELM重构结果

图4 墨西哥帽子三维图形重构结果

(2) 训练样本生成。极限学习机训练过程需要大量训练样本，为生成训练样本，在给定横纵坐标范围内以0.5为步长用rand函数随机产生Q个网格节点作为神经网络的输入，Q=1 000，网格节点坐标矩阵[x_randy_rand],用plot(x_rand,y_rand,‘*’)语句绘制随机生成的网格节点如图5所示，其中训练样本输入为P，训练样本期望输出为T，即每个网格节点对应的高度。

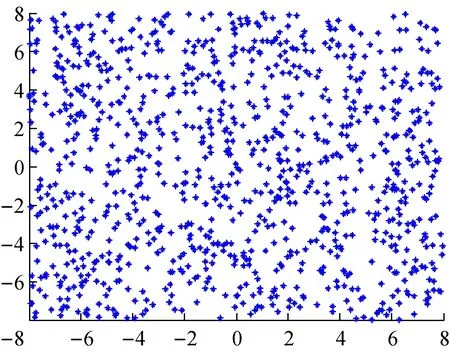
图5 随机生成的网格节点分布图

训练样本生成过程程序为：

(3) 基于ELM、MLS-ELM和R-ELM的三维图形重构仿真。本实验案例通过ELM、MLS-ELM和R-ELM 3种算法对墨西哥帽子三维图形进行重构仿真。原始ELM训练过程部分程序为：

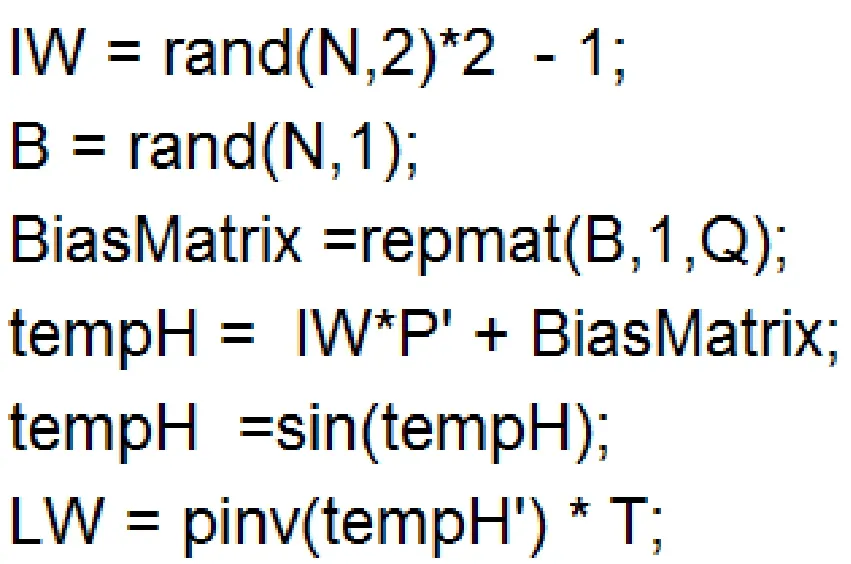
其中：N为隐藏层神经元个数，N=50，IW为输入权值，B为隐藏层神经元偏置矩阵，激活函数为sin(x)，tempH为根据式(1)求得的隐藏层输出，LW为根据式(5)求得的输出矩阵。

经以上训练过程得输出权值矩阵LW，通过下列所示程序进行墨西哥帽子三维图形重构仿真，Or_Elm_Zout即神经网络的最终输出，原始ELM算法实现墨西哥帽子三维图形重构仿真结果如图4(b)所示。

无权正则极限学习机的输出权值矩阵为

(13)

由式(11)得:

(14)

(15)

式中，c1和c2的值分别取2.5和3。正则极限学习机对墨西哥帽子三维图形重构结果如图4(d)所示。

(4) 重构结果误差分析。如图4所示，ELM、MLS-ELM和R-ELM 3种算法均可以对墨西哥帽子三维图形进行重构，为了比较3种算法的性能，将实测值和期望值之间的绝对误差进行对比，图6所示为ELM、MLS-ELM和R-ELM对墨西哥帽子三维图形重构实验的绝对误差曲线。由图6可见，MLS-ELM算法的重构效果最佳。另外，将均方根RMSE作为重构误差的衡量标准，同时将训练时间和测试时间也进行了对比，具体结果见表1。

由表1虚拟重构实验结果对比可知，ELM、MLS-ELM和R-ELM重构误差的均方差RMSE分别为0.061 7、0.015 5和0.039 8，MLS-ELM的误差最小。图6和表1 对比结果表明，MLS-ELM算法和R-ELM算法在重构精度和泛化能力上都优于原始的ELM算法，但这两种算法增加了计算复杂度，延长了训练时间。

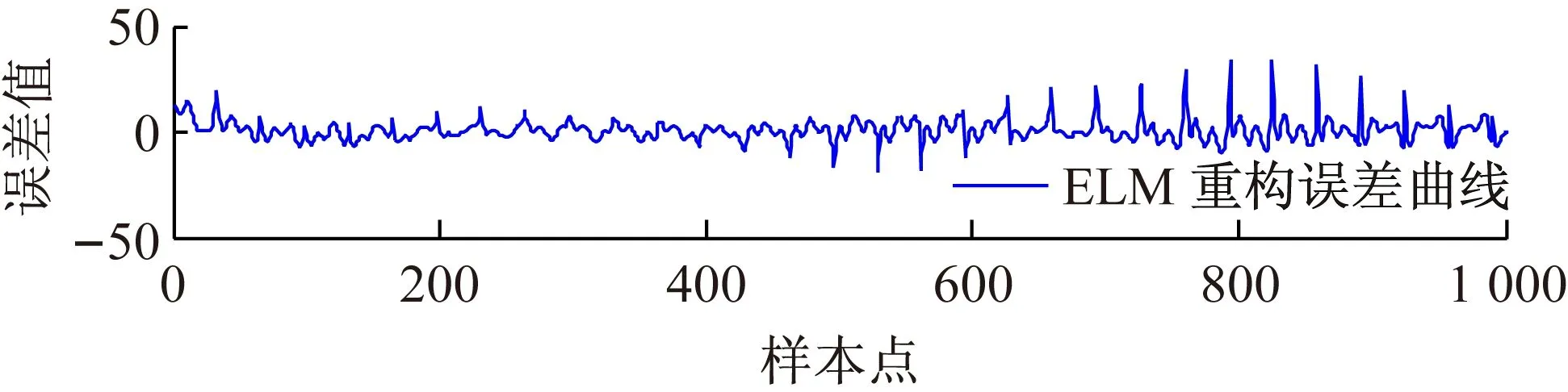
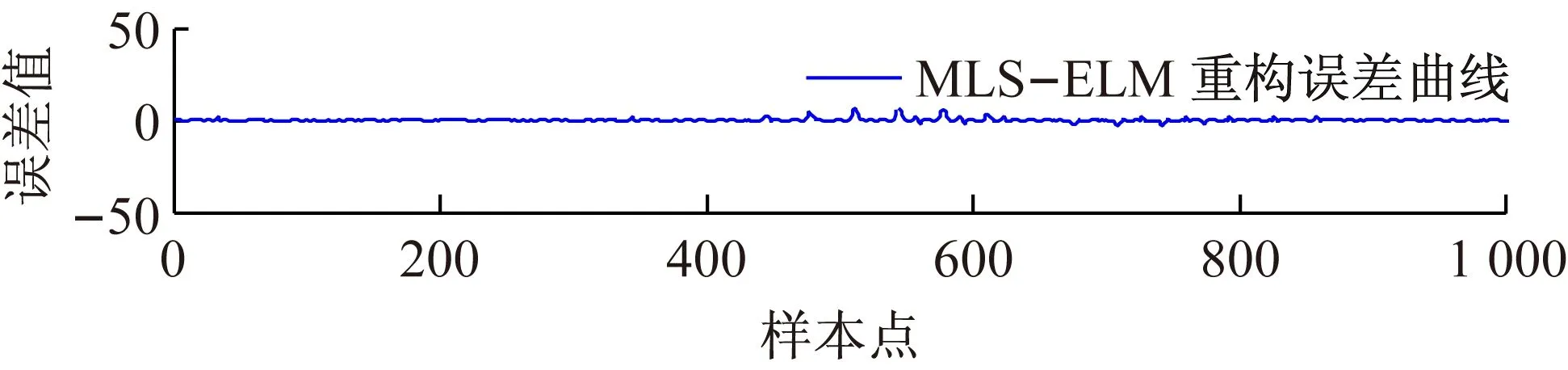
图6 ELM、MLS-ELM和R-ELM重构误差曲线

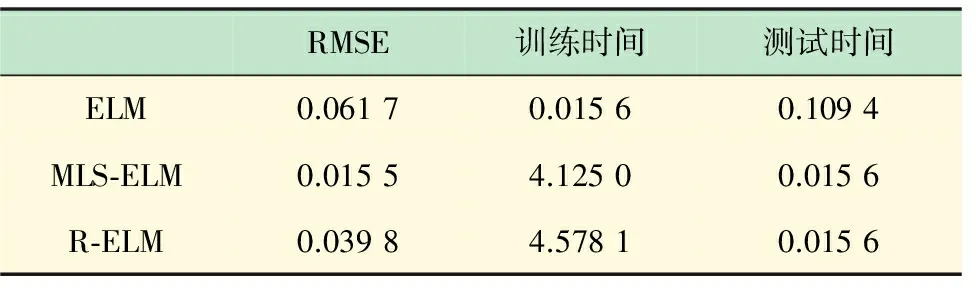
表1 ELM、MLS-ELM和R-ELM虚拟仿真实验结果对比

4 结 论

本文设计了墨西哥帽子三维图形重构虚拟仿真实验，通过两种极限学习机的优化算法，以三维图形重构实验为平台进行了实测，并将该实验案例应用于本科教学，达到了以下教学目的：

(1) 掌握神经网络的基本原理和应用，了解ELM算法的优势，仿真过程直观地呈现出三维图形的重构效果，让实验教学更为生动具体，可将极限学习机算法推广到更多的应用领域，如人体三维重构、手势识别等。

(2) 介绍移动加权极限学习机和正则极限学习机优化算法，掌握优化算法的设计，为学生在以后的工程设计中拓宽思路，缩短设计周期。

(3) 采用Matlab作为仿真环境，熟练使用Matlab编程软件，掌握基于Matlab虚拟仿真实验的设计。

(4) 通过对墨西哥帽子三维图形虚拟仿真实验结果进行比较，掌握虚拟仿真实验结果对比时参数的选择和分析方式。

通过虚拟仿真实验的开展可以开阔学生的眼界，提升学生的科研兴趣，鼓励学生以所学知识为基础拓展到更宽、更广的知识体系中，同时提倡学生积极参加科研竞赛，锻炼动手能力，为学生从学校毕业步入工作岗位奠定理论基础，提高实践技能。

[1] 王艳芬,丛潇雨,王 刚,等. 基于Simulink的Chirp- UWB通信系统综合实验设计[J]. 实验室研究与探索, 2015(7):90-93，234.

[2] 周 品.Matlab神经网络设计与应用[M].北京：清华大学出版社，2013,55-62.

[3] Huang GB, Wang DH, Lan Y.Extreme learning machines : a survey[J]. Int J Mach Learn & Cyber, 2011(2):107-122.

[4] Huang G B,Qin Y Z,Chee K S. Extreme learning machine：Theory and applications[J]. Neuroco- mputing, 2006,70: 489-501.

[5] Wang Feng，Dai Shu-guang. 3-D Reconstruction based on binocular stereo vision [J]. Proc of SPIE,2009， 7283: 728331.

[6] 温 颖,刘思远,张 玲.视觉优化的移动三维图形自适应重构技术研究[J].计算机工程与设计,2013(8): 2862-2866.

[7] 王冬欣,李 哲. 基于VTK的CT图像三维重建与可视化[J]. 实验室研究与探索,2015(8):108-111.

[8] 褚玉晓，邵 彧.三维图形重建算法的仿真研究[J].计算机仿真，2013,30(3):403-407.

[9] 姜大志. 计算机视觉中三维重构的研究与应用[D].南京：南京航空航天大学,2002.

[10] 王 年.三维重构中关键算法研究[D].合肥：安徽大学,2005.

[11] Kang J Q, Lu S, Gong W B,etal. A Complex network based feature extraction for image retrieval[C]∥IEEE International Conference on Image Processing,2014: 2051-2055.

[12] 赵文华,张文涛,杜欣慧. 形相似的ELM在电铁短期负荷预测中应用[J]. 实验室研究与探索, 2013(11): 279-282,328.

[13] Lancaster P, Salkauskas K. Surface generated by moving least squares methods [J]. Math Com-Putation, 1981, 37: 141-158.

[14] Ren H P, Cheng Y M, Zhang W. Researches on the improved interpolating moving least-squaresmethod [J]. Chinese Journal of Chemical Engineering, 2010, 27 (6): 1021-1029.

[15] Deng W, Zheng Q, Chen L. Regularized extreme learning machine[C]∥Computational Intelligence and Data Mining, 2009. CIDM’09. IEEE Symposium on. IEEE, 2009:389-390.

[16] Suykens J A K,De Brabanter J,Lukas L,etal.Weighted least squares support vector machines:Robustness and sparse approximation[J]. Neurocomputing, 2002,48(1): 85-105.

·名人名言·

知识是一座宝库,而实践则是开启宝库的钥匙。

——托马斯·富勒

Virtual Simulation Experiment Research for 3D Graphics Reconstruction Based on Extreme Learning Machine

CHENLong，QIEXiaomei，HUANGXinjing

(School of Electronic Information, Hangzhou Dianzi University, Hangzhou 310018, China)

In view of the limitations of over fitting and small generalization ability caused by extreme learning machine (ELM), it uses moving least square extreme learning machine (MLS-ELM) and regularized extreme learning machine (R-ELM) optimization algorithm to balance structure risk and empirical risk caused by extreme learning machine (ELM). The design improves the generalization ability of the ELM. It uses MLS-ELM and R-ELM to conduct the virtual simulation experiment about the reconstruction of 3D graphics of the Mexican hat function. This experiment shows that MLS-ELM and R-ELM can effectively reduce the reconstruction error. This simulation experiment can be used in the neural network and Matlab virtual simulation teaching, and plays a positive role in improving the students’ autonomous learning ability and the programming ability.

extreme learning machine; Lagrange multiplier method; 3D graphics reconstruction; virtual simulation experiment; ability cultivation

2016-03-25

浙江省2013年高等教育课堂教学改革项目——(kg2013125)； 浙江省2015年度高等教育教学改革项目(jg2015060)

陈 龙(1979-)，男，山东宁阳人，硕士，副教授，研究方向为嵌入式系统设计与应用、神经网络与机器学习。

Tel.：0571-86915094； E-mail：chenlong@hdu.edu.cn

G 642.423

A

1006-7167(2017)02-0102-05