基于混凝土三维球形随机骨料模型的氯离子扩散细观数值模拟

王元战，何明伟，李青美，吴林键

（1.天津大学水利工程仿真与安全国家重点实验室，天津300072；2.高新船舶与深海开发装备协同创新中心，天津300072）

基于混凝土三维球形随机骨料模型的氯离子扩散细观数值模拟

王元战1，2，何明伟1，2，李青美1，2，吴林键1，2

（1.天津大学水利工程仿真与安全国家重点实验室，天津300072；2.高新船舶与深海开发装备协同创新中心，天津300072）

当前对于海洋环境下混凝土结构中氯离子的扩散问题的数值模拟研究大多停留在宏观层面，没有考虑混凝土细观结构的影响。针对这一问题，建立了混凝土三维球形随机骨料细观模型，并基于该模型提出了混凝土中氯离子扩散细观数值模拟方法。混凝土三维球形随机骨料模型以随机过程理论为依据，考虑了骨料粒径大小和位置分布的随机性，更接近实际情况；基于该模型的氯离子扩散细观数值模拟方法能够从细观层面反应混凝土中氯离子扩散规律，可以作为混凝土中氯离子扩散研究的重要手段。在此基础上研究了混凝土细观结构对氯离子扩散的影响，结果表明：界面过渡区厚度和扩散系数越大时，经扩散进入混凝土中的总体氯离子含量越多，但混凝土浅层区域内的氯离子含量越少；随着粗骨料体积分数的增加，混凝土中相同深度处的氯离子浓度降低。

海洋环境；混凝土；随机骨料；氯离子扩散；数值模拟；界面过渡区

海洋环境中，混凝土结构受到海水中氯离子侵蚀，引起钢筋锈蚀，进而导致结构承载力下降甚至破坏的情况屡见不鲜，海洋环境下混凝土的耐久性已成为港口工程设计中不可忽视的重要问题。混凝土中氯离子的扩散是一个长期缓慢的过程，目前常用的研究方法主要有物模试验和数值模拟两大类。物模试验的实施周期较长，会消耗大量的时间、成本和精力；数值模拟方法较为简单、方便且高效。然而，目前对于该问题的数值模拟研究大多停留在宏观层面，难以体现混凝土的细观结构及其性质。混凝土的细观结构包括骨料、水泥砂浆和界面过渡区（ITZ）［1］三部分，这三者的各项性质均可能会对混凝土中氯离子的扩散产生较大的影响［2］。为了能够更加深入的研究混凝土中氯离子传输的特征和性质，学者们对该问题的研究逐渐由宏观视野转向细观层面。其中，彭国军［3］用有限元的方法研究了二维八边形骨料面积分数对氯离子扩散的影响；吴静新［4］通过二维随机骨料有限元模型研究了界面过渡区对氯离子扩散的影响；王学礼［5］用二维随机骨料模型研究了骨料面积分数对氯离子扩散的影响；田兴长［6］基于三维复合球模型用ANSYS软件中的热传导分析模块，研究了混凝土中氯离子扩散的过程，探讨了ITZ和粗骨料体积分数对氯离子扩散的影响。前三者研究都是建立在二维模型基础上，与实际的三维情况有一定的差异，而田兴长［6］的混凝土模型中的骨料粒径是通过富勒级配人为计算得到的，骨料位置也是人为确定的，没有实现骨料粒径大小和位置分布的随机性，与实际情况存在差异。

本文采用数值模拟手段，建立了混凝土三维球形随机骨料模型。考虑了骨料粒径大小和位置分布的随机性并在三维情况下进行研究，更接近实际情况。在此基础上，提出了基于混凝土三维球形随机骨料模型的氯离子扩散细观数值模拟方法。用此数值模拟方法研究混凝土细观模型中氯离子扩散规律，探究混凝土细观结构中界面过渡区厚度、界面过渡区扩散系数以及粗骨料体积分数对混凝土中氯离子扩散性质的影响。

1 混凝土三维球形随机骨料模型

在研究混凝土中氯离子的扩散问题中，为方便实际度量计算和公式推导，常把其中骨料的形状简化为规则的几何图形，Yang［7］的试验中把骨料简化成圆柱形，本文将混凝土中骨料简化为球形。Kreijger［8］指出，混凝土表层下0.1 mm内是净浆层，不含任何骨料，0.1～5 mm之间的砂浆层中含有少量的粗骨料，超过5 mm以后则是包含正常骨料分布的混凝土介质。为了在细观层面上更加深入地研究混凝土中氯离子的扩散与骨料及其界面过渡区之间的关系，本文提出了一种骨料粒径大小和位置分布都更接近实际情况的混凝土三维球形随机骨料模型，并详细叙述了该模型的具体实施步骤，为混凝土中氯离子扩散的细观数值模拟奠定基础。

该模型包含混凝土中骨料粒径的随机生成以及骨料在混凝土试件中的随机投放这两大步骤，通过MATLAB编程实现。

1.1 混凝土中骨料粒径的随机生成

（1）定义混凝土试件的三维空间尺寸X、Y、Z，骨料最大粒径dmax、最小粒径dmin以及粗骨料体积占混凝土试块总体积的比例，即粗骨料的体积分数r；

（2）计算出三维区域内骨料总体积V；

（3）采用等体积骨料级配，P（d）为关于粒径d的颗粒数累计分布函数，表达式如下

用随机数函数unifrd（0，1）生成一个［0，1］区间上的随机数a，令P（d）=a，求解方程得到直径di；（4）判断是否满足dmin≤di≤dmax的限制条件，若不满足重复步骤（3），如果满足进行下一步；（5）计算已生成骨料总体积vi；

（6）当vi≥V时，表明已生成的骨料体积已达到预设的要求，保存满足该条件的所有骨料粒径数据，并进行下一步计算，否则应重复步骤（3）、（4），直至vi满足要求。

1.2 骨料在混凝土试件中的随机投放

（1）将1.1节第（6）步中生成的骨料粒径数据进行降序排列，后续投放按照粒径从大到小的顺序依次进行；

（2）为了模拟实际情况下混凝土中骨料分布的特点，取混凝土试件数值模型表层以下3 mm范围内不含粗骨料，3 mm以后粗骨料随机的分布在混凝土试件当中。故球心坐标（xi，yi，zi）应满足条件：xi∈［di/2+3，X-di/ 2-3］，yi∈［di/2+3，Y-di/2-3］，zi∈［di/2+3，Z-di/2-3］，在上述区域内随机的生成第i个球形骨料的球心坐标（xi，yi，zi）；

（3）在指定区域内随机的生成第i+1个球形骨料的球心坐标（xi+1，yi+1，zi+1）。并分别判断第i+1个骨料所形成的球形区域是否与前面已经生成的i个骨料中任意一个球形区域重叠，若不满足，则重新生成新的球心坐标，并再次判断直至满足要求为止，此时记录并保存该坐标信息。其中，判别是否重叠的依据如公式（2）。式中：{Li+1}为第i+1个骨料球心与前面i个骨料球心之间的空间距离向量，其中Li+1，1、Li+1，2、...、Li+1，i分别为第i+1个骨料球心与第1、第2、...、第i个骨料球心间的空间距离；γ为骨料范围影响系数，取1.05［9］。

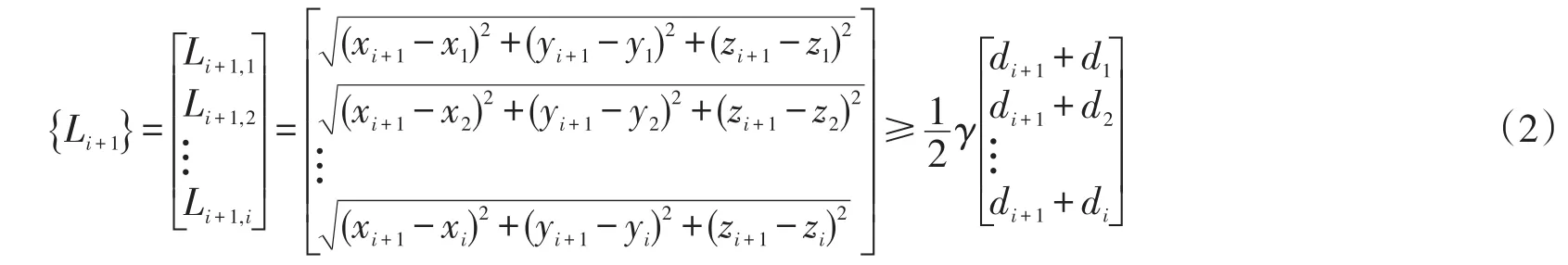
（4）根据第（4）步所述，依次将所有已生成的不同粒径的全部骨料在设定的区域内投放完毕；

（5）最终，输出混凝土试件中骨料投放的随机分布图。

1.3 程序流程

根据以上1.1、1.2节中所述，绘制得到生成混凝土三维球形随机骨料模型的程序流程图，如图1所示。

1.4 随机模型结果验证

根据以上步骤及流程，计算得到不同体积分数情况下，100×100×100 mm3混凝土试件中骨料随机分布的结果。为了验证本文中混凝土三维球形随机骨料模型的正确性，取骨料粒径d范围为：5.0～31.5 mm，混凝土骨料体积分数r分别为：0.2、0.3和0.4，计算得到混凝土试件中三维球形骨料的随机分布结果，如图2所示。

将图2所示的数值模拟结果与《水运工程混凝土施工规范（JTS202-2011）》［10］中规定的累积筛余量要求进行对比，结果如表1所示。

由表1中可知，本文所提出的随机模型计算所得到的混凝土骨料级配满足规范要求，可验证本文随机模型计算结果的正确性与合理性。同时，从图2中也可以看到，随机生成的混凝土骨料级配合理，位置分布均匀，表明该混凝土三维球形随机骨料模型能够很好地模拟混凝土中骨料的级配和分布。

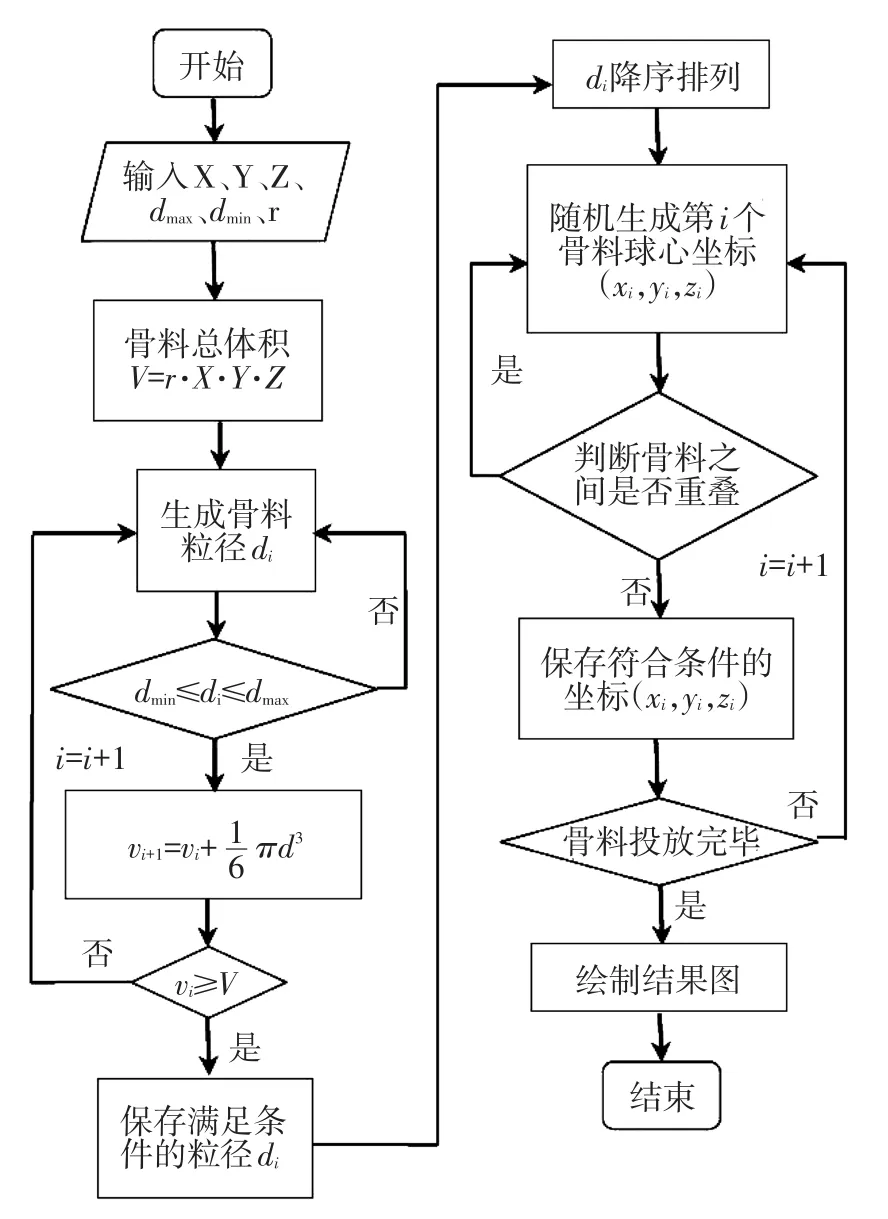
图1 三维球形随机骨料模型流程图Fig.1 Flow diagram of three-dimensional spherical random aggregate model

2 基于混凝土三维球形随机骨料模型的氯离子扩散细观数值模拟

本文采用有限元分析软件COMSOL中的稀物质传递模块来对混凝土中氯离子的扩散过程进行数值模拟，以研究氯离子在混凝土中的扩散规律。Fick第二定律是目前公认的混凝土中氯离子扩散的控制方程［11］，COMSOL中稀物质传递模块求解基本方程正是Fick定律，该模块能够很好地模拟氯离子在混凝土中的扩散，Fick定律公式如下

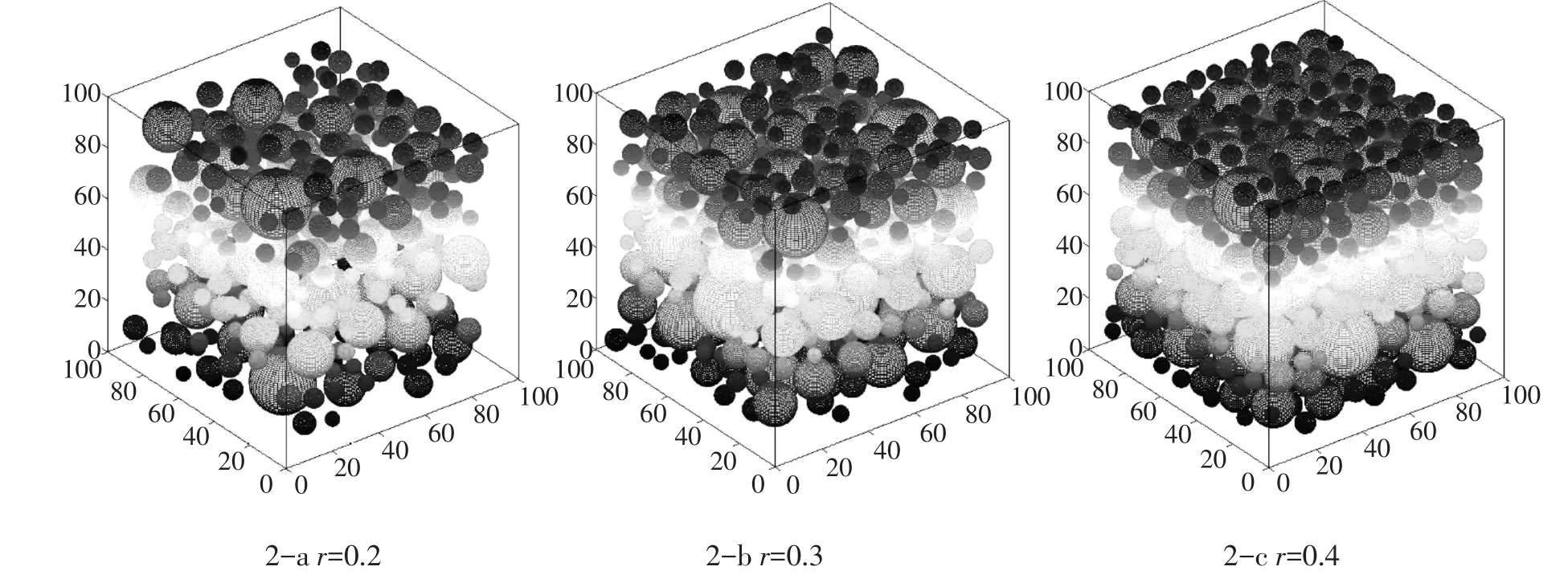
图2 不同r混凝土三维球形随机骨料分布图Fig.2 Distribution diagram of three-dimensional spherical random aggregate concrete with differentr

将前文中通过图1流程计算得到的混凝土三维球形骨料的粒径大小及球心坐标信息导入到COMSOL软件中，并在骨料周围设置界面过渡区，建立混凝土试件的三维有限元数值模型，然后输入相应的计算参数并划分网格，利用瞬态求解器进行计算，从而实现对混凝土中氯离子扩散的细观数值模拟。软件中需要输入的参数主要为：界面过渡区厚度hITZ（mm）；混凝土试件表面的氯离子浓度Cs（%）（用表面氯离子质量占胶凝材料质量的比例来表示）；砂浆、骨料以及界面过渡区的氯离子扩散系数D0、Da以及DITZ（m2/s）。值得注意的是：本文仅探讨氯离子从混凝土试件的单个面侵蚀后，其内部氯离子的扩散规律，在数值模拟过程中，将氯离子侵蚀面以外的其余5个面均设置为无通量。

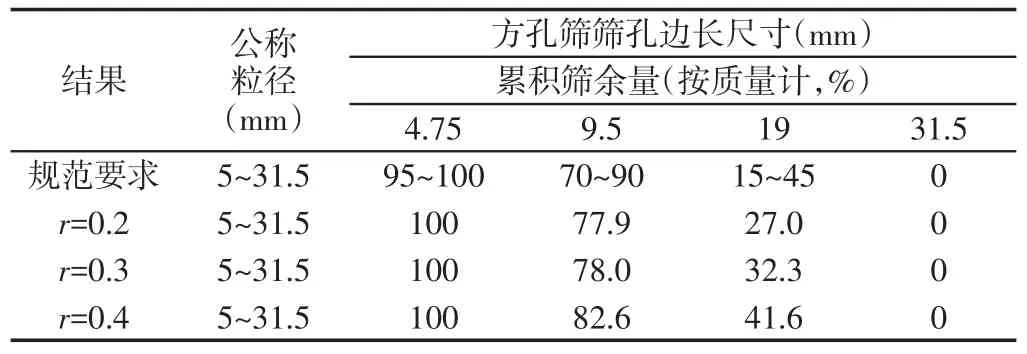
表1 骨料级配Tab.1 Aggregate

为了验证本文有限元数值模拟的正确性，将刘恒［12］在研究混凝土中氯离子扩散规律的物模试验中实测浓度数据拟合得到的结果作为相应的参数输入到COMSOL中进行计算，将计算得到的不同深度的氯离子浓度值与刘恒［12］物模试验中的实测值进行对比。物模试验中，混凝土试件的尺寸为100×100×100 mm3，粗骨料体积分数为0.3，除侵蚀以外的5个表面上涂抹环氧树脂后，置于3.5%的氯化钠溶液中浸泡170 d，然后用混凝土打磨机从预留的渗透面开始逐层磨粉，并采用CL-E氯离子含量快速测定仪测量得到每一层混凝土中的氯离子浓度。

对实测试验结果进行拟合，得到170 d时的D0=1.44×10-12m2/s、Cs=1.04112%，刘恒［12］文中取hITZ=0.04 mm，DITZ拟合为D0的30倍，即DITZ=4.32×10-11m2/s。将以上参数输入到COMSOL软件建立的模型中，设定求解时间为170 d，计算得到混凝土试件中氯离子浓度分布，如图3所示。对不同深度的截面取浓度的面平均值，得到不同深度处混凝土中氯离子浓度的分布，并将数值模拟结果与刘恒［12］的物模试验实测的浓度数据进行对比，如图4所示。

从图4中可以看出，混凝土试件在深度10 mm以前数值模拟结果与试验数据的吻合情况良好，当深度超过10 mm以后，数模的结果较试验结果而言更小。单看试验数据，深度超过10 mm以后部分的氯离子浓度基本恒定，这与实际情况中氯离子浓度随深度的增加而递减的规律不符，其主要原因可归结为试验过程中的误差或测量仪器对浓度较小的溶液不敏感所致。

综上所述，本文数值模拟计算所得的混凝土中氯离子扩散结果与物模试验中的实测数据能够相吻合，从而验证了本文仿真方法的正确性与可行性，该基于三维球形随机骨料模型的混凝土细观数值模拟方法是混凝土中氯离子扩散研究的有效手段。

图3 氯离子浓度分布图Fig.3 Distribution diagram of chloride concentration

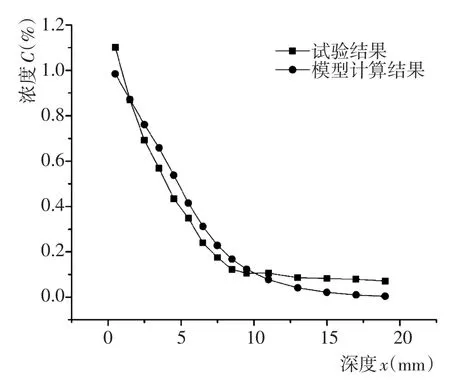
图4 氯离子浓度模型计算值与试验值对比Fig.4 Comparison of model and experiment results of chloride concentration

3 细观结构对氯离子扩散影响

混凝土的细观结构包括粗骨料、水泥砂浆和界面过渡区（ITZ）三部分，这三者的各项性质均可能会对混凝土中氯离子的扩散产生影响。为了探究混凝土细观结构各方面对氯离子扩散的影响，本文应用前文所述的基于三维球形随机骨料模型的混凝土细观数值模拟方法，探讨不同界面过渡区厚度和氯离子扩散系数以及粗骨料体积分数对混凝土中氯离子扩散的影响。

3.1 界面过渡区厚度对氯离子扩散的影响

根据Basheer［13］研究可知，界面过渡区厚度hITZ取值范围为0～100 μm，界面过渡区扩散系数DITZ的取值范围为砂浆扩散系数D0的0～100倍。为了研究界面过渡区厚度（hITZ）对氯离子扩散的影响，取界面过渡区氯离子扩散系数DITZ/D0=30（即ITZ的扩散系数为砂浆扩散系数的30倍），设置hITZ的取值分别为：无界面过渡区（hITZ=0）、10 μm、40 μm、70 μm和100 μm，其余参数与2.1节中一致。

图5由于纵坐标中所标示的氯离子浓度范围较大，图中各曲线浓度差别相对看来并不明显，故绘制不同hITZ与无ITZ情况下的不同深度处氯离子的浓度差，如图6所示。从图中可以看出，ITZ的存在会造成大致在深度为9 mm以前的氯离子浓度降低，9～30 mm范围内氯离子浓度增加，且随着hITZ的增大，氯离子浓度变化幅度越大。图7为不同hITZ情况下，混凝土模型中的总体氯离子浓度，从计算结果中可以明显看出：随着hITZ的增加，扩散进入混凝土模型中的总体氯离子含量增大，且增大趋势基本呈线性。

3.2 界面过渡区扩散系数对氯离子扩散的影响

为探讨不同界面过渡区扩散系数（DITZ）对混凝土中氯离子扩散的影响，取界面过渡区厚度为40 μm，设置DITZ/D0的值分别为：无界面过渡区（DITZ/D0=1）、5、30、50、100。其余参数与2.1节中一致。

从图8、图9中可以看出：DITZ/D0的增大将会导致大致在深度为9 mm以前氯离子浓度降低，9～30 mm范围内氯离子浓度增加，且随着DITZ/D0的增加，氯离子浓度的降低或增加幅度也越来越大，这与界面过渡区厚度对氯离子扩散的影响相似。从图10中可以明显的看出：随着DITZ/D0的增加，经扩散进入混凝土中的总体氯离子浓度也相应增加，当DITZ/D0＞50之后，该趋势逐渐变缓。

由图5～图10可知，DITZ和hITZ对氯离子在混凝土中的扩散有着明显的影响，随着hITZ和DITZ的增加，经扩散进入混凝土中的氯离子总浓度增加，但是深度小于9 mm范围内混凝土中的氯离子浓度反而减小，且在接近5 mm位置处氯离子的浓度差值达到最大。究其原因是在混凝土小于5 mm的浅层区域粗骨料含量较深层少［7］，界面过渡区体积分数相对于内部区域小，则小于5 mm的浅层区域内氯离子的扩散强度也相对较小，故扩散进入浅层区域的氯离子浓度比从该区域向更深层扩散的氯离子浓度小，这便导致了当hITZ和DITZ越大时，小于9 mm范围内混凝土中的氯离子浓度反而越小。

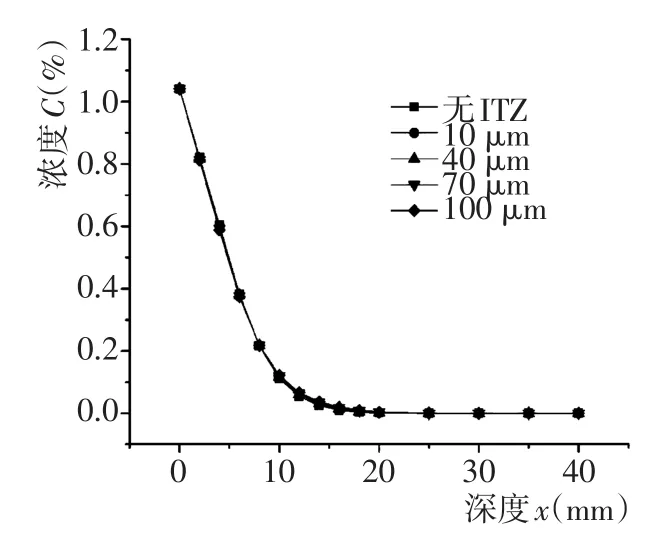
图5 不同hITZ氯离子浓度随深度的变化Fig.5 Chloride concentration variation along depth with differenthITZ

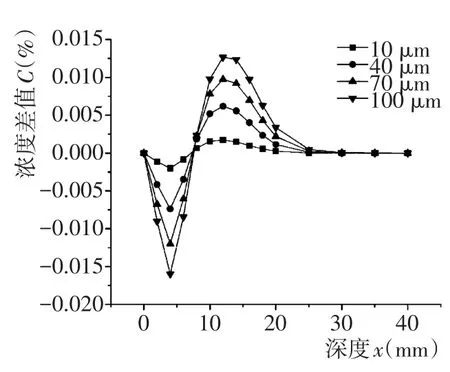
图6 不同hITZ与无ITZ之间氯离子的浓度差Fig.6 Concentration difference between models withhITZand no ITZ

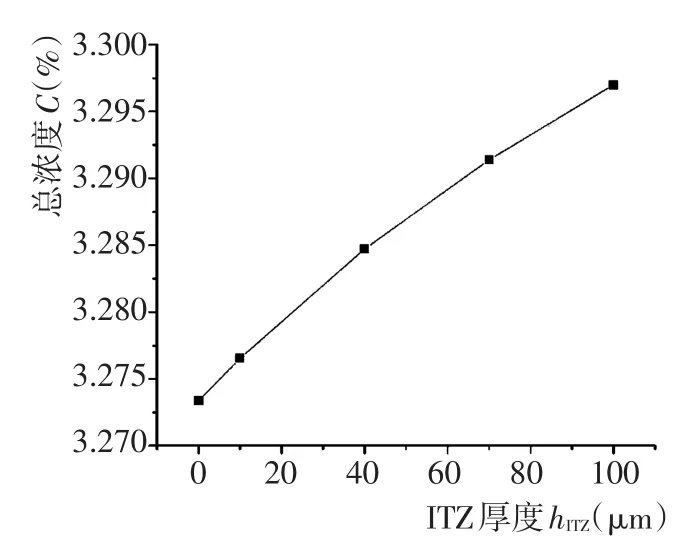
图7 不同hITZ混凝土模型中的总体氯离子浓度Fig.7 Total chloride concentration in concrete with differenthITZ

图8 不同DITZ/D0氯离子浓度随深度的变化Fig.8 Chloride concentration variation along depth with differentDITZ/D0

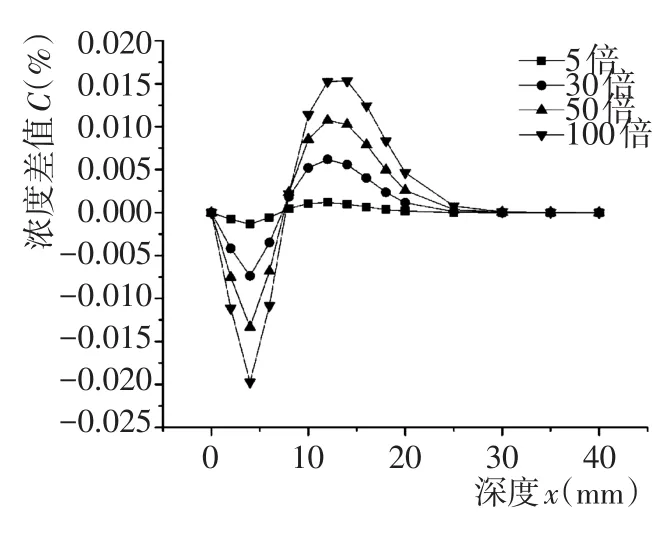
图9 不同DITZ/D0与无ITZ之间氯离子的浓度差Fig.9 Concentration difference between models with differentDITZ/D0and no ITZ

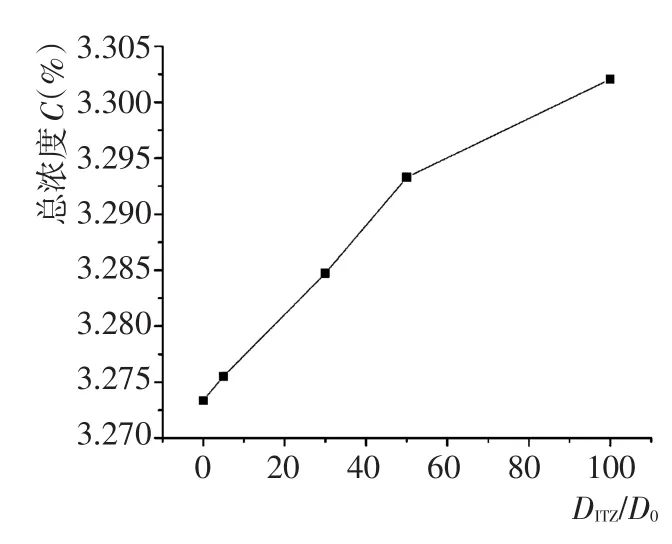
图10 不同DITZ/D0时混凝土模型中的总体氯离子浓度Fig.10 Total chloride concentration in concrete with differentDITZ/D0

3.3 粗骨料体积分数对氯离子扩散的影响

Shah［14］经研究总结得出混凝土中粗骨料对氯离子扩散能力存在3个方面的影响，分别为：稀释效应、曲折效应和界面过渡区效应。其中前两者会阻碍混凝土中氯离子的扩散，而界面过渡区则会起到提高氯离子扩散的作用。界面过渡区的体积分数取决于粗骨料的体积分数r以及界面过渡区的厚度hITZ［15］。故粗骨料体积分数对混凝土内氯离子扩散会产生一定的影响，下面探究其影响规律。

采用前文所述基于三维球形随机骨料模型的混凝土细观数值模拟方法，研究不同粗骨料体积分数对混凝土中氯离子扩散的影响。其中，hITZ取40 μm，DITZ取30D0，设置粗骨料的体积分数r分别为：0（纯砂浆）、0.1、0.2、0.3、0.4，其余参数与2.1节中一致。

由图11可以看出170d达到的扩散深度大致为20 mm，在扩散深度范围内随着r的增加，混凝土试件相同深度处的氯离子浓度逐渐降低，由图12可知，与纯砂浆相比各深度处的浓度降低值随着r增大而增大，大约在扩散深度中间位置（9 mm）处浓度差达到最大值，说明粗骨料体积分数越大混凝土中氯离子扩散作用越弱，且对扩散深度中间位置的浓度影响最大。

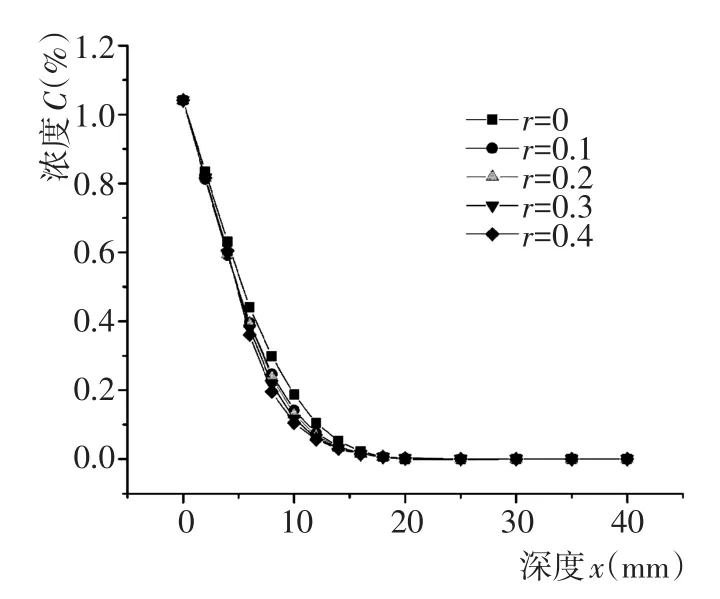
图11 不同r条件下氯离子浓度随深度的变化Fig.11 Chloride concentration variation along depth with differentr

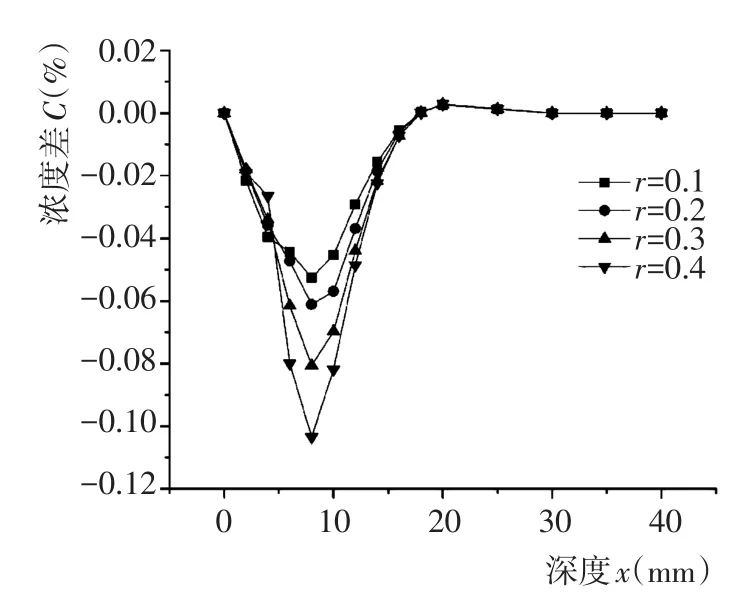
图12 不同r与纯砂浆之间氯离子的浓度差Fig.12 Concentration difference between models with differentrand pure mortar

4 结语

（1）用MATLAB建立了混凝土三维球形随机骨料模型，考虑了混凝土中骨料粒径大小和分布的随机性及表层骨料分布的不均匀性，并在三维模型中进行计算，更接近真实情况。该模型为进一步混凝土中氯离子扩散的细观数值模拟奠定了基础。

（2）在混凝土三维球形随机骨料模型基础上进行氯离子扩散的细观数值模拟，并将数值计算结果与试验结果进行对比，吻合情况良好。该基于混凝土三维球形随机骨料的氯离子扩散细观数值模拟方法能够较好的模拟实际情况下混凝土中氯离子的扩散过程。

（3）界面过渡区厚度和扩散系数对混凝土中氯离子扩散过程有明显的影响，且作用效果相似。hITZ和DITZ越大，进入混凝土的氯离子总量越多，但9 mm之前相同深度处氯离子浓度反而越小。

（4）粗骨料体积分数增大，混凝土中相同深度处的氯离子浓度逐渐降低，大约在扩散深度中间位置处降低值达到最大。

［1］Breton D，Carles A，Ballivy G，et al.Contribution to the formation mechanism of the transition zone between rock-cement paste［J］. Cement and Concrete Research，1993，23（2）：335-346.

［2］Wittmann F H.Structure of Concrete with Respect to Crack Formation［C］//Wittmann F H editor.Fracture Mech-anics of Concrete. London/New York：Elsevier，1983：43-74.

［3］彭国军.考虑骨料形状时混凝土氯离子扩散系数预测的数值方法［J］.水利水电科技进展，2009，29（6）：13-16. PENG G J.A Numerical Method for Predicting the Chloride Diffusion Coefficient of C with Aggregate Shape［J］.Advances in science and Technology of Water Resources，2009，29（6）：13-16.

［4］吴静新.混凝土中氯离子传输模型及其数值研究［D］.哈尔滨：哈尔滨工业大学，2012.

［5］王学礼.混凝土材料的氯离子迁移细观数值模拟［J］.公路交通科技（应用技术版），2011，10：68-71. WANG X L.Micro-scale Numerical Simulation for Chloride Diffusion of concrete material［J］.Highway Taffic Sience and Technology（Application Technology Edition），2011，10：68-71.

［6］田兴长.混凝土中氯离子扩散系数预测的三维模拟法［D］.杭州：浙江工业大学，2010.

［7］Yang C C，Su J K.Approximate migration coefficient of interfacial transition zone and the effect of aggregate content on the migration coefficient of mortar［J］.Cement and Concrete Research，2002，32（10）：1 559-1 565.

［8］Kreijger P.The skin of concrete-composition and properties.Materials and structures，1984，17（100）：275-283.

［9］Bazant Z P，TABBARA M R，KAZEMI M T，et al.Random particle model for fracture of aggregate or fiber composites［J］.Journal of Engineering Mechanics，ASCE，1990，116（8）：1 686-1 705.

［10］JTS202-2011，水运工程混凝土施工规范［S］.

［11］Collepardi M，MARCIALIS A.Penetration of chloride ions into cement paste and concrete［J］.Journal of the American Ceramic Society，1972，10（55）：534-535.

［12］刘恒.粗骨料对混凝土中氯离子扩散影响试验研究［D］.天津：天津大学，2015.

［13］Basheer L，Kropp J.Assessment of the durability of concrete from its permeation properties：a review［J］.Construction and building materials，2001，15（2）：93-103.

［14］Shah S P.High Performance Concrete，Past，Present and Future［C］//LEUNG C k，LI Z，DING J T，et al.High Performance Concrete-Workability，Strength and Durability.Hong Kong：Hong Kong University of Science and Technology，2000：3-29.

［15］Caré S.Influence of aggregates on chloride diffusion coefficient into mortar［J］.Cement and Concrete Research，2003，33（7）：1 021-1 028.

Micro-scale numerical simulation for chloride diffusion based on concrete threedimensional spherical random aggregate model

WANG Yuan-zhan1,2,HE Ming-wei1,2，LI Qing-mei1,2,WU Lin-jian1,2
（1.State Key Laboratory of Hydraulic Engineering Simulation and Safety,Tianjin University,Tianjin300072,China;2.Collaborative Innovation Center for Advanced Ship and Deep Sea Exploration,Tianjin300072,China）

In marine environment,the chloride diffuses in concrete structure,now most numerical simulations of which remain in macro level,ignoring the influence of concrete meso structure.Concerning this issue,the threedimensional spherical random aggregate model was developed.Based on the model,the method of meso-scale numerical simulation for chloride diffusion in concrete was proposed.The three-dimensional spherical random aggregate model takes account of the randomness of aggregate diameter and position,according to random process theory. The method of meso-scale numerical simulation for chloride diffusion based on this model is able to reflect chloride diffusion law in meso-scale.It can be used as an important measure to study chloride diffusion in concrete.The effects of meso structure on the process of chloride diffusion in concrete were studied using this method.The results indicate that as the thickness and diffusion coefficient of ITZ increase,the total chloride contents diffused into concrete specimen increase accordingly,while the chloride concentration in the superficial zone decreases.With increasing of the volume fraction of coarse aggregate,the chloride concentration of the same depth decreases.

marine environment;concrete;random aggregate;chloride diffusion;simulation;ITZ

U 641；O 242.1

A

1005-8443（2017）01-0059-07

2016-09-06；

2016-09-30

交通运输部交通建设科技项目（2014328224040）；国家自然科学基金（51279128）；国家自然科学基金创新研究群体科学基金（51321065）。

王元战（1958-），男，天津市人，教授，博士生导师，主要从事港口海岸与近海结构设计理论和方法、土与结构相互作用、结构振动分析理论和方法等方面的研究工作。

Biography：WANG Yuan-zhan（1958-），male，professor.