基于岭回归的压力传感器高精度测量模型研究*

龙 军,关 威,汪旭东,陈 君

(北京控制工程研究所,北京 100094)



基于岭回归的压力传感器高精度测量模型研究*

龙 军*,关 威,汪旭东,陈 君

(北京控制工程研究所,北京 100094)

硅压阻式压力传感器测量精度易受环境温度影响,为提高压力传感器测量精度,提出基于岭回归方法的高精度压力测量回归模型,采用新的测量方式从压力元件桥路提取压力传感器温度、压力变化的信息,建立了压力传感器桥路输出、桥路电阻与被测压力三者之间的回归模型,并利用Bootstrap方法对模型参数进行显著性检验,提高模型的稳定性。实验结果显示该方法可大幅度消除温度对压力测量精度的影响,使压力测量精度从±0.6% FS提高到±0.03% FS。

压力传感器;温度补偿;岭回归;Bootstrap;参数显著性检验

硅压阻式压力传感器具有灵敏度高、动态相应快、测量精度高的特点,并具有较好的介质相容性和长期稳定性,因而在工业过程控制、生物制药、航空航天等领域有着广泛的应用。由于半导体材料本身对温度非常敏感,使得传感器的输出不仅受压力的影响,还会受环境温度变化的影响,从而产生温度漂移,加上传感器本身存在的非线性,使传感器的测量精度大大降低[1]。因而,为提高压力传感器的测量精度,就需要对压力传感器进行温度补偿,以满足高精度压力测量的需求。

针对硅压阻式压力传感器存在的温度漂移和非线性问题,常用的补偿方法有硬件补偿法和软件补偿法[2-6]。硬件补偿法是指采用硬件电路的方法对压阻桥路进行补偿,比如在桥臂上或桥路外串、并联固定电阻或热敏电阻的方式对压力传感器进行温度和非线性补偿。硬件补偿方法通常只能抵消温度引起的失调和灵敏度漂移,而且补偿过程复杂、调试困难、通用性差。软件补偿方法则是利用传感器的温度和压力信息,运用相应的数学算法来构建回归模型。软件补偿算法通常具有补偿精度高,通用性强的特点,有利于压力传感器的实际工程应用[7-9]。

压力传感器的软件补偿通常可以转化为多元回归建模的问题,在进行多元回归建模时,通常会遇到多重共线性问题,多重共线性指的是多元回归模型自变量间存在一定程度的相关现象,当回归方程的自变量之间出现多重共线性关系时,如果采用最小二乘法建立回归模型,则模型的精确性和稳定性都得不到保证,模型的预测精度会大大降低,所建立的回归模型将没有实用价值[10-13]。

为克服多重共线性在回归建模中带来的问题,以岭回归为代表的有偏估计方法得到了人们的重视。岭回归是在1962年由Heer等人提出的一种改进的最小二乘估计方法,它针对最小二乘回归中自变量存在多重共线性时估计性能变差的缺陷而提出的一种方法,岭回归通过引入岭参数改变最小二乘法中对回归系数估计的不稳定性,进而使得参数估计值更加更加稳定,提高建模的准确性[10-11]。

Bootstrap法是美国斯坦福大学统计系教授Efron于1979年提出的一种再抽样方法[10],该方法以原始数据为基础的模拟抽样统计推断法,可用于研究数据的统计量分布特征,特别适用于那些难以用常规方法导出对参数的区间估计,假设检验等问题。由于岭回归模型参数的精确分布难以确定,因而无法用参数估计的方法对其模型参数进行统计学检验,但基于Bootstrap的非参数统计学方法却不受总体分布的限制,可用来检验模型中每个自变量参数是否有统计学意义。

本文提出了基于岭回归方法的压力传感器高精度测量模型,首先从压力元件桥路提取传感器温度、压力变化信息,并采用岭回归方法进行建模,再结合Bootstrap方法对模型参数进行显著性检验,最终建立了压力传感器桥路输出、桥路电阻与被测压力三者之间的多元非线性回归模型。与传统的高精度压力传感器温度补偿方法相比,本文提出的方法无需布置额外的温度传感器进行测温,克服了传感器之间存在温度差的问题,能有效提高压力传感器的测量精度。

1 温度补偿原理

在实际进行温度补偿的过程中,温度变化引起的输出量变化和压力变化引起的输出量变化具有耦合性,很难区分输出变化是由于温度引起还是压力变化引起的。因此,要对硅压阻式压力传感器进行补偿,首先要想办法获得能够反映温度以及压力变化的特征参数,然后采用多元回归方法对传感器温漂和非线性误差进行补偿。

如图1所示为硅压阻式压力传感器的测量电路,它是硅片上布置的4个应变电阻条组成的惠斯通电桥,电桥中的4个应变桥臂阻值不仅会随压力的变化而变化,还会随温度的变化而变化。

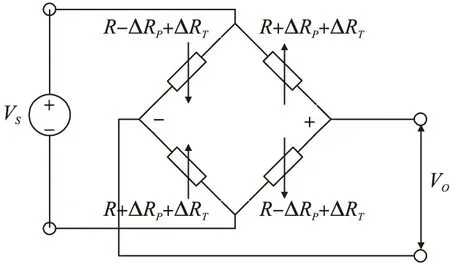
图1 硅压阻式压力传感器的桥式电路

图1中,设R为在温度为0 ℃,压力为0 Pa时(绝压传感器)的桥臂阻值,R为恒定值;ΔRP为受压力后的桥臂阻值变化量;ΔRT为受温度影响的变化量;VS为桥路上施加的恒定电压;VO为桥路输出电压信号。由此可以得到:

(1)

由式(1)可以看出,桥路输出电压信号会同时受到温度、压力的影响。因此需要找到能反映温度变化的量。从桥式电路很容易可以知道,桥路并联电阻RB可以表示为R+ΔRT,是一个与温度相关的量。可以看出,RB与压力产生的应变没有关系,仅与温度引起的附加应变有关。因此,可以利用RB作为反映温度变化的参数,也即采用压力传感器本身的进行温度测量。这样做的好处是:直接利用压力传感器桥路元件本身来反映温度变化,避免由于外加温度传感器而导致测量温度和压阻传感器应变膜片的实际温度存在差异给补偿带来误差,提高了补偿的精度。由于省去了外加的温度传感器,这样便简化了温度补偿的压力传感器硬件电路。

上述分析是建立在假设四桥臂电阻初始阻值、温度系数、压阻系数一致基础上的,而在实际应用中,被测压力为零时,4个应变桥臂初始阻值以及电阻的温度系数和压阻系数不可能完全一致,电桥输出电压可表示为:

(2)

桥臂的并联总电阻RB表示为:(R1+R2)∥(R3+R4),有

(3)

定义SB=VO/I,其中I为流过桥路的总电流,I=VRB/RB,结合式(1)可得,

(4)

则式(1)可写成

(5)

由于R1、R2、R3、R4均会受到压力P和温度T的影响,是温度和压力的二元函数,因此RB和SB也可以表示为P、T的二元函数的形式。

(6)

式(6)消去变量T可得,

P=f(RB,SB)

(7)

式中:P为被测压力,根据上述部分得出的结论可以知道,利用压力传感器敏感桥路本身对温度和压力敏感的特点,SB主要反映压力的影响,而RB则主要反映温度的变化,因此可以将SB和RB作为压力传感器温度补偿模型的特征参数,建立式(7)所示的温度补偿模型,下面将介绍如何从实际测量电路中获得SB和RB。

为了利用桥路元件本身对温度敏感的特性来进行温度补偿,需要在测量电路中引入高精密低温漂参考电阻RREF。则流过参考电阻的电流与流过桥路的总电流相等,可表示为I=VREF/RREF。则SB、RB可以由下式确定:

(8)

(9)

因此,在实际应用中,通过测量电路中3个差分电压信号VO、VRB、VREF,然后通过式(8)、式(9)计算得到SB和RB的值。通过建立SB、RB和压力P之间的多元回归模型,从而得到硅压阻式压力传感器的温度补偿模型。

2 压力传感器温度补偿模型

由上述内容可知,式(7)所述的模型不再依赖外部温度传感器来测量温度,而是利用测量桥路自身的参数SB和RB来进行温度补偿。

上述模型具有两个自变量,本文采用最常用的多项式回归模型来建立SB和RB与P的映射关系。设待求多项式中SB的最高次数为m-1,RB的最高次数为n-1,同时SB和RB之间有耦合关系,则具有如下形式:

(10)

式中:Cij为上述模型的系数矩阵。上式向量表达形式为:

(11)

式中:

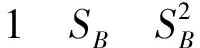
(12)

(13)

(14)

为了求解上述线性方程的系数矩阵Cij,可将上述向量表达式转化为线性回归的正规方程表达式,可以写成:

Y=XβT

(15)

2.1 岭回归模型建立

设x1,…,x2,…,xm是标准化变量,XTX为x1,x2,…,xm的相关系数矩阵。回归系数β的最小二乘估计为β=(XTX)-1XTY,定义岭回归估计:

β(k)=(XTX+kI)-1XTY

(16)

式中:β为岭回归估计,其中I为单位矩阵,k(0≤k≤∞)为岭参数。

当自变量之间存在复共线关系时,|XTX|≈0,最小二乘估计求得的回归系数会出现与实际情况很不符合的异常现象,而XTX+kI接近异常的程度会比XTX接近异常的程度小得多,即最小二乘在复共线状态下的偏差部分虽然为零,但它的方差部分却很大,最终致使它的均方误差很大,而岭回归是牺牲无偏性,换取方差部分的大幅度减少,最终降低其均方误差。因而,岭回归估计可改变最小二乘对回归参数估计的不稳定性[4]。

2.2 模型阶数确定

由于式(10)所示的多项式模型是对式(7)的近似,所以多项式模型阶数应当在满足拟合精度的前提下取最小,尽可能降低模型计算量。为此,选择单点最大拟合误差、误差平方和作为约束条件来确定模型阶数,式(17)所示为单点最大拟合误差需小于给定允许误差e,误差平方和如式(18)所示。

(17)

(18)

上述多元多项式模型阶数确定的具体步骤归纳如下:①在传感器的工作范围内选取足够多足够均匀的点,测量传感器的静态特性标定数据,获得标定试验数据集,所用标定仪器测量精度应高于待设计压力测量系统精度;②估计m和n的初始范围,对于每一个m、n组合,利用岭回归方法计算其系数矩阵C和满足约束条件式(17)和式(18);③在满足拟合精度满足第1条的m、n组合中选m+n最小的一组作为最终多项式的次数,如果m+n取最小有两种或两种以上不同选择方案,选择使式(17)最小的一组。

2.3 基于Bootstrap的模型参数检验

本文所用方法为利用Bootstrap对岭回归模型参数进行显著性检验[10]。其步骤如下:

①由原始数据集建立的岭回归模型

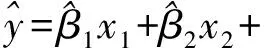
(19)

拟检验的H0假设为:

H0:=0

(20)

H1:≠0

(21)

②在原数据集S中随机抽取1个样本点(yi(1),xi1(1),xi2(1),…,xip(1)),观察其值后,放回原数据集S。再从原数据集中抽取第2个样本点,观察其数值,重复n次,从而得到一个Bootstrap样本

S(1)={(yi(1),xi1(1),xi2(1),…,xip(1)

(22)

式中:i=1,2,3,…,n。

③以Bootstrap样本S(1)做岭回归,得到的岭回归模型为

y=β1(1)x1+β2(1)x2+…+βp(1)xp

(23)

④重复步骤(2)、(3)N次,得到N组回归系数。本文取N=200。

{β1(b),β2(b),…,βp(b)} (b=1,2,…,N)

(24)

⑤记

(25)

式中:b=1,2,…,N;j=1,2,…,p。

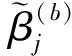
⑥判别准则为:

如果

(26)

则拒绝H0假设,βi显著不为0,这时称自变量xj有统计学意义;否则不拒绝H0假设,自变量无统计学意义,xj未通过显著性检验。

将所有有统计学意义的自变量在原数据集上重新建立岭回归方程,重复步骤①～步骤⑥,直到剩下所有的变量都通过假设检验。

2.4 实验验证

实验中选用某型硅压阻式压力传感器作实验元件,其测量范围为0～2.0 MPa,在-10 ℃～55 ℃范围内元件本身测量精度为在±1% FS以内,采用补偿算法后目标测量精度要求为优于±0.05% FS。

按照图2所示构成测量电路,桥路供电电压为5 V,本实验的压力传感器电桥桥臂电阻R=2.8 kΩ。为了尽量减小电桥的功耗和发热,需要将流过电桥电阻的电流控制在1 mA左右,所以电桥参考电阻RREF取2.2 kΩ,精度为0.05%,温漂5×10-6/℃。

图2 硅压阻式压力传感器温度压力提取电路示意图

实验中,将压力传感器放置于温度箱中,在-10 ℃～55 ℃范围内共设置7个温度点(分别为-10 ℃、-5 ℃、5 ℃、15 ℃、25 ℃、35 ℃、55 ℃)。对于每个温度点,选取6个压力点(分别为0.12MPa、0.6MPa、1.0MPa、1.4MPa、1.6MPa、2.0MPa)加载压力,进行传感器的静态特性标定。即在每个温度下,当温度变化率小于2 ℃/h时认为温度稳定,此时可对压力传感器进行加压标定,采用16bitA/D数据采集卡对电压信号VO、VRB、VREF压进行采集。实验中采用的压力校验仪是美国Paroscientific公司的Model745-500A,压力校验范围0～3.45MPa,精度为0.008%FS。

实验共获得42个数据点,表1所示为不同温度点下的实验数据,其中SB为反映压力变化的参数;RB为反映温度变化的参数。数据处理过程中,首先对原始数据进行必要的预处理,如多次测量取平均值、剔除病态数据,之后选取合适的归一化函数分别将计算获得的参数SB、RB进行归一化,有助于降低数值计算中的误差。

表1 温度标定数据

利用以上实验数据,根据式(10)进行建立二元多项式回归模型,估计m、n的范围在2～8之间,对每一组m、n分别求取系数矩阵Cij、式(17)和式(18)。

在测量误差小于0.05%FS的条件下,最终确定模型阶数为m=5,n=4,结合Bootstrap方法对该模型参数进行检验,检验结果如图3所示。图3为检验水平a取0.05,k=5×10-7,k=5×10-8,k=5×10-9时的参数检验情况,根据式(26)判别式可知当k=5×10-8时,20个自变量系数全部通过显著性检验,所得到的模型参数最稳定,得到的系数矩阵Cij如表2所示。

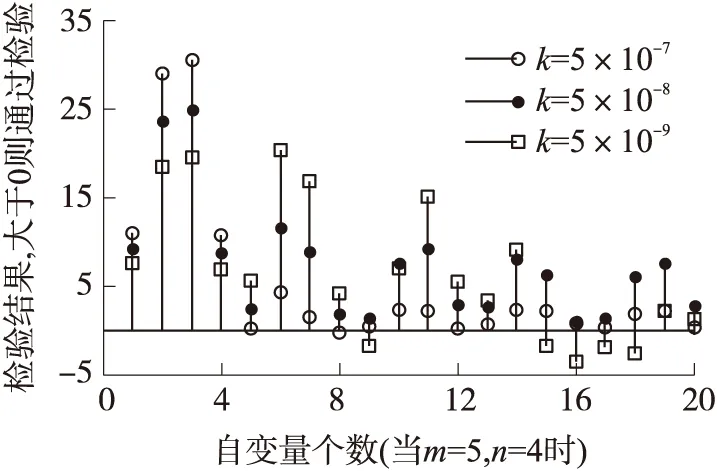
图3 基于Bootstrap方法的模型参数检验结果

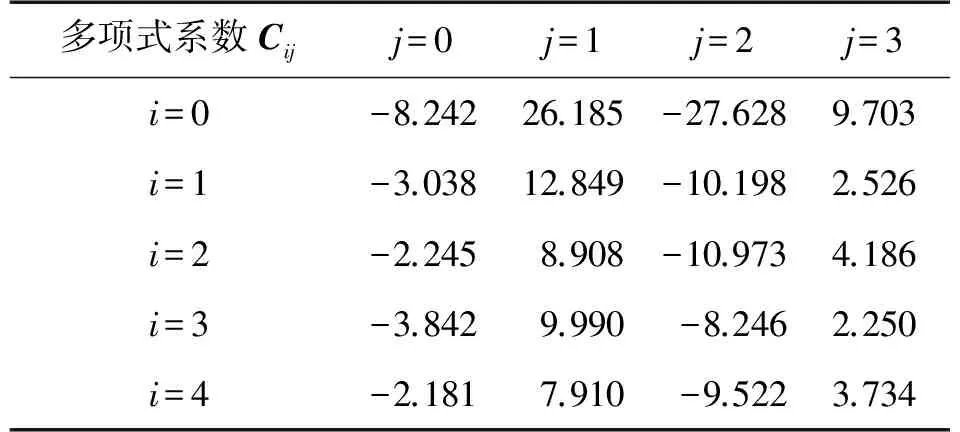
多项式系数Cijj=0j=1j=2j=3i=0-8．24226．185-27．6289．703i=1-3．03812．849-10．1982．526i=2-2．2458．908-10．9734．186i=3-3．8429．990-8．2462．250i=4-2．1817．910-9．5223．734

为了验证模型的有效性,选取-10 ℃～55 ℃范围内的测试数据对补偿前后的测量模型进行对比,误差分布如图4所示,图中error表示拟合预测误差。由图4可看出,在-10 ℃～55 ℃范围工作范围内,补偿前传感器的测量误差在±0.6% FS左右,采用本文方法补偿后最大测量误差在±0.03% FS左右。

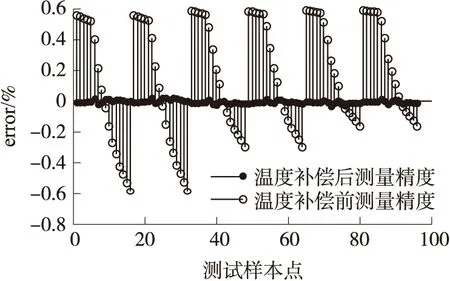
图4 压力测量模型预测误差分布

3 结束语

本文针对硅压阻式压力传感器存在的温度漂移和非线性问题,利用压力传感器元件桥路本身对温度、压力敏感的特点,采用从压力元件桥路提取传感器温度、压力变化信息的测量方式,结合岭回归方法和Bootstrap参数检验,建立了压力传感器桥路输出、桥路电阻与被测压力三者之间的岭回归模型,并有效解决了岭回归方法中参数选择问题。最终获得压力测量模型大幅度消除了温度对压力测量精度的影响,压力测量精度由±0.6% FS提升到±0.03% FS。该方法可以避免安装额外的温度传感器,克服了传感器之间存在温度差的问题,同时补偿算法所需的数据存储量也远少于多点插值法,具有很强的工程实用价值。

[1] Bhat K N. Silicon Micromachined Pressure Sensors[J]. Journal of the Indian Institute of Science,2011,87(1):115-131.

[2] Aryafar M,Hamedi M,Ganjeh M M. A Novel Temperature Compensated Piezoresistive Pressure Sensor[J]. Measurement,2015,63:25-29.

[3] 韩迪,袁正兴. 压力传感器温度漂移及补偿方法研究[J]. 测控技术,2013,32(增刊):280-282.

[4] Bruschi P,Dei M,Piotto M. A Method to Compensate the Pressure Sensitivity of Integrated Thermal Flow Sensors[J]. Sensors Journal IEEE,2010,10(10):1589-1597.

[5] 杨雪,刘诗斌. 压力传感器温度补偿各种算法的比较分析[J]. 电子设计工程,2013,21(10):90-92.

[6] Tsai H H,Hsieh C C,Fan C W,et al. Design and Characterization of Temperature-Robust Piezoresistive Micro-Pressure Sensor with Double-Wheatstone-Bridge Structure[C]//Symposium on Design,Test,Integration and Packaging of Mems/moems. IEEE,2009:363-368.

[7] Liu Y T,Da-Cheng X U,Guo S W. A Temperature Compensation Algorithm of Piezoresistive Pressure Sensor and Software Implementation[C]//IEEE International Conference on Mechatronics and Automation. 2013:1738-1742.

[8] 孙艳梅,苗凤娟,陶佰睿. 基于PSO的BP神经网络在压力传感器温度补偿中的应用[J]. 传感技术学报,2014(3):342-346.

[9] 杨遂军,康国炼,叶树亮. 基于最小二乘支持向量机的硅压阻式传感器温度补偿[J]. 传感技术学报,2016,29(4):500-505.

[10] 王惠文. 偏最小二乘回归方法及其应用[M]. 国防工业出版社,1999.

[11] 魏传华,郭双,王肖南. 部分线性模型的随机约束岭估计[J]. 数学的实践与认识,2014,44(13):249-254.

[12] 黄文珂. 多元回归建模过程中共线性的诊断与解决方法[D]. 哈尔滨:哈尔滨工业大学,2012.

[13] 杨楠. 岭回归分析在解决多重共线性问题中的独特作用[J]. 统计与决策,2004,(3):14-15.

龙 军(1985-),男,湖北荆门人,2013年获浙江大学控制科学与工程专业工学博士学位,现为北京控制工程研究所高级工程师,主要从事传感器信号处理及高精度测量电路研究,longjun20811307@gmail.com。

Study on High Accuracy Measurement Model of Pressure Sensor Based on Ridge Regression*

LONGJun*,GUANWei,WANGXudong,CHENJun

(Beijing Institute of Control Engineering,Beijing 100094,China)

The measurement accuracy of silicon piezoresistive pressure sensor is easily affected by environment temperature. To improve the measurement accuracy of the pressure sensor,a regression model based on ridge regression was proposed,a novel measurement method was adopted to extract the pressure and temperature information from the pressure sensor,and then a regression model between the pressure sensor bridge output,bridge resistance and the measured pressure was built. To improve the stability of the regression model,the Bootstrap method was used for a statistical significance test of the model parameters. Experimental results show that the proposed method can greatly eliminate the effect of temperature on pressure measurement,so that the accuracy of pressure measurement can be improved from ±0.6% FS to ±0.03% FS.

pressure sensor;temperature compensation;ridge regression;bootstrap;parameter significance test

项目来源:十二五民用航天项目(E020415)

2016-08-01 修改日期:2016-11-13

TP212

A

1004-1699(2017)03-0391-06

C:7230

10.3969/j.issn.1004-1699.2017.03.010