悬架减震器非线性特性对汽车拖车组合系统稳定性的影响

张 宁 琚安建 李鹏程 殷国栋

(东南大学机械工程学院, 南京 211189)

悬架减震器非线性特性对汽车拖车组合系统稳定性的影响

张 宁 琚安建 李鹏程 殷国栋

(东南大学机械工程学院, 南京 211189)

为了研究汽车拖车组合系统中牵引车悬架减震器非线性引起的时变特性的谐波动态轴载对系统动态稳定性的影响,提出了一种带有双轴拖车系统的线性单轨模型．根据推导出的有效轴载量化动态轴载,并采用基于时频域分析的方法识别系统的时变参数．实验研究表明,此谐波效应具有时变性．设计了一种基于车辆横摆角速度的仿真方法来模拟道路实验中观测到的谐波效应,并通过仿真分析谐波幅值和相位对系统动态临界车速的灵敏度,初步验证了考虑悬架减震器非线性特性引起的谐波动态轴载对汽车拖车组合系统稳定性影响的理论分析．

车辆动力学;汽车拖车组合系统;非线性特性;时变谐波效应;动态稳定性

任何具有非线性特性的元件均会把谐波响应引入到系统中,在有谐波电流的电力系统中这种谐波效应尤为普遍．鉴于机械系统与电力系统之间的相似性原理,谐波效应也会在机械结构(如一个有非线性弹簧或阻尼的质量弹簧阻尼系统)中产生．由于车辆悬架零部件的设计具有非对称性,这种非线性特性将激发谐波效应并对车辆系统的稳定性造成影响．目前对悬架减震器的阻尼系数的大小、长期工作导致的阻尼系数降低造成的影响进行了研究,但仅限于对乘用车的静态稳定性的影响,而对汽车拖车组合系统(car-trailer combinations, CTC)稳定性影响的研究还局限在水平面动力学的范围内．

为此,本文研究了非线性特性激发谐波效应对汽车拖车组合系统动态稳定性的影响．首先采用基于时频域分析(time-frequency analysis, TFA)的参数识别方法(parameter identification method, PIM)[1]来描述并量化动态轴载的谐波特性,然后通过仿真来研究这种谐波的幅值和相位对系统稳定性的影响．而实验和仿真结果都表明,该谐波动态轴载的幅值和相位对CTC动态稳定性具有显著的影响．

1 汽车拖车组合系统稳定性

车辆在水平面上的稳定性分为静态稳定性和动态稳定性[2]．静态稳定性关注的是系统的稳态行为．动态稳定性关注的是系统的瞬态行为．一个带有较大的振荡响应的静态稳定系统很难控制,如处在动态临界稳定状态下的CTC．在水平面上的动态失稳通常表现为蛇行运动或摆动[2]．由于谐波动态轴载是车辆系统瞬态行为的表现,故本文主要探讨谐波动态轴载对CTC系统动态稳定性的影响．

1.1 单轨模型

图1 带有双车轴拖车的汽车拖车组合系统的线性单轨模型

根据牛顿定理及牵引车与拖车在铰接点的耦合关系,建立如下线性系统的动力学方程[3]:

(1)

式中,M和E为系统定常参数矩阵；D为包括纵向速度vx的系统矩阵;x为系统状态向量;u为系统输入参数．状态方程可化为

(2)

A(vx)=M-1D(vx),B=M-1E

(3)

式中,矩阵A为纵向速度vx的函数;B为定常参数矩阵．采用式(2)可描述CTC系统的动态特性．

1.2 系统动态稳定性分析

通过引入拉普拉斯算子计算出系统状态方程(2)的特征值,基于纵向速度vx进行根轨迹分析可以发现,当vx超过一定数值时,CTC表现为横摆角速度动态失稳．此时vx被定义为系统动态临界速度vcrit,可以用vcrit来描述动态稳定性的边界．实际上,动态临界速度与系统的零横摆阻尼比紧密相关,两者均由系统参数的工作点决定．而系统的惯性参数和几何参数通常不变,所以对一个确定的CTC系统来说,很少考虑其对系统动态稳定性的影响．由于车轴侧偏刚度在水平动力学和垂向动力学之间起到连接桥梁的作用,因此对vcrit的灵敏度分析显得至关重要．文献[4]发现,牵引车和拖车后车轴侧偏刚度的增加能提高系统的动态稳定性,而牵引车前车轴侧偏刚度的增加则会降低系统的动态稳定性,拖车前车轴侧偏刚度对系统的动态稳定性几乎没有影响．

2 悬架减震器非线性特性

悬架零部件的非线性特性在很大程度上由其非对称特性造成的[5-7]．由于压缩性效应、气穴现象[8]或是机械、电子元件的失效等现象的存在,这种失效引起的非对称性特性在元件运动循环中的某些特定位置尤其严重[9]．

为了解释车辆系统中非线性特性引起谐波的物理机理,图2总结了减震器非线性特性引起的谐波动态轴载．这里的减震器是指汽车悬架上的减震器．图中，sd和vd分别为减震器的垂向位移和速度；Fd为阻尼力；t为时间；Fd,L和Fd,R分别表示左、右两侧减震器的阻尼力,Fd,sum和Fz,sum分别为同轴左、右两侧减震器的阻尼力之和以及相应的轴载．

图2(a)、(d)、 (g)中通过Fd-vd图、Fd-sd图和F-t图描述了理想线性减震器的特性,不存在不对称性和谐波动态轴载．图2(b)、 (e)、 (h)描述了一个实际中分段线性正常减震器,在汽车拖车中组合系统引入了非对称性和谐波动态轴载．此时,引起谐波动态轴载的是设计中存在的非对称性,即预料中的非线性．图2(c)、(f)、(i)描述的是一种减震器失效[8]现象,即在一个运动循环周期中,压缩开始时和回弹结束时的阻尼力非常小．此种情况下,对于具有谐波响应的车辆系统来说,任一时刻在同一轴上只有一侧的减震器失效．如果同时考虑同轴左、右两侧减震器,将会引入谐波动态轴载．所以,图2中的正常和失效特性都会在车辆系统中引入谐波动态轴载．

(a) 线性Fd-vd图

(b) 正常Fd-vd图

(c) 失效Fd-vd图

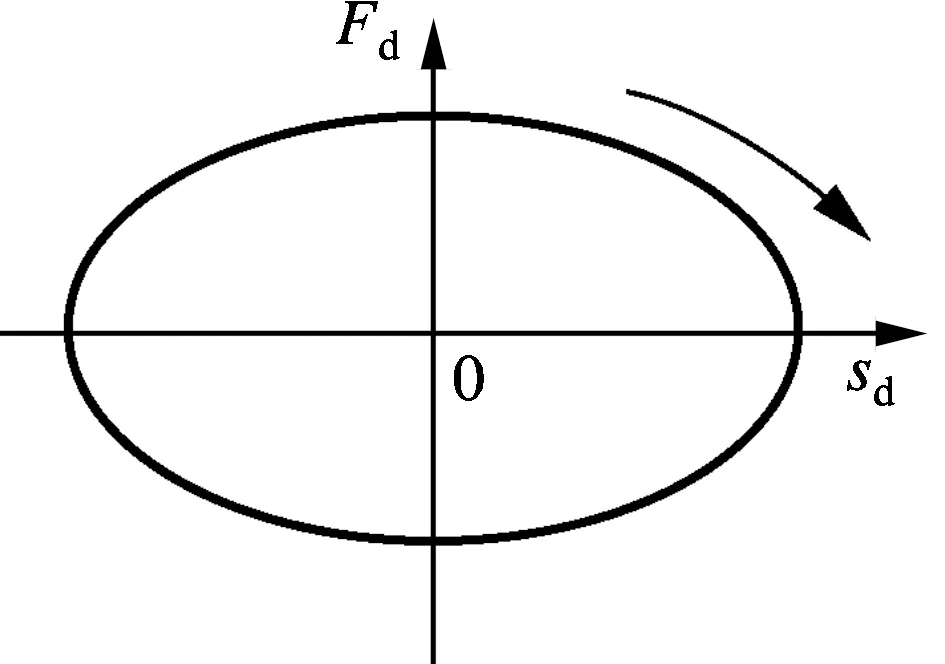
(d) 线性Fd-sd图

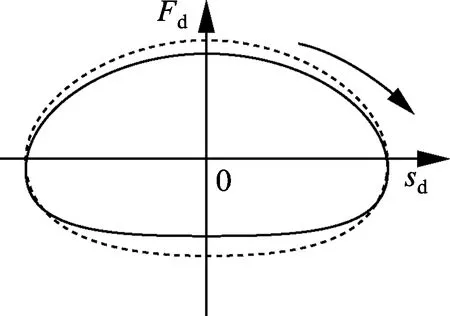
(e) 正常Fd-sd图

(f) 失效Fd-sd图

(g) 线性F-t图

(h) 正常F-t图

(i) 失效F-t图

3 非线性引起的谐波动态轴载

在稳定性分析中,定义车轴侧偏刚度为轴侧向力与相应的轴侧偏角的比值．侧偏刚度可以通过在时域或频域中参数识别方法得到[10-11]．本文将对一种由悬架减震器非线性特性引起的谐波动态轴载进行分析和量化．

3.1 谐波效应现象

(a) 相位偏移为0°

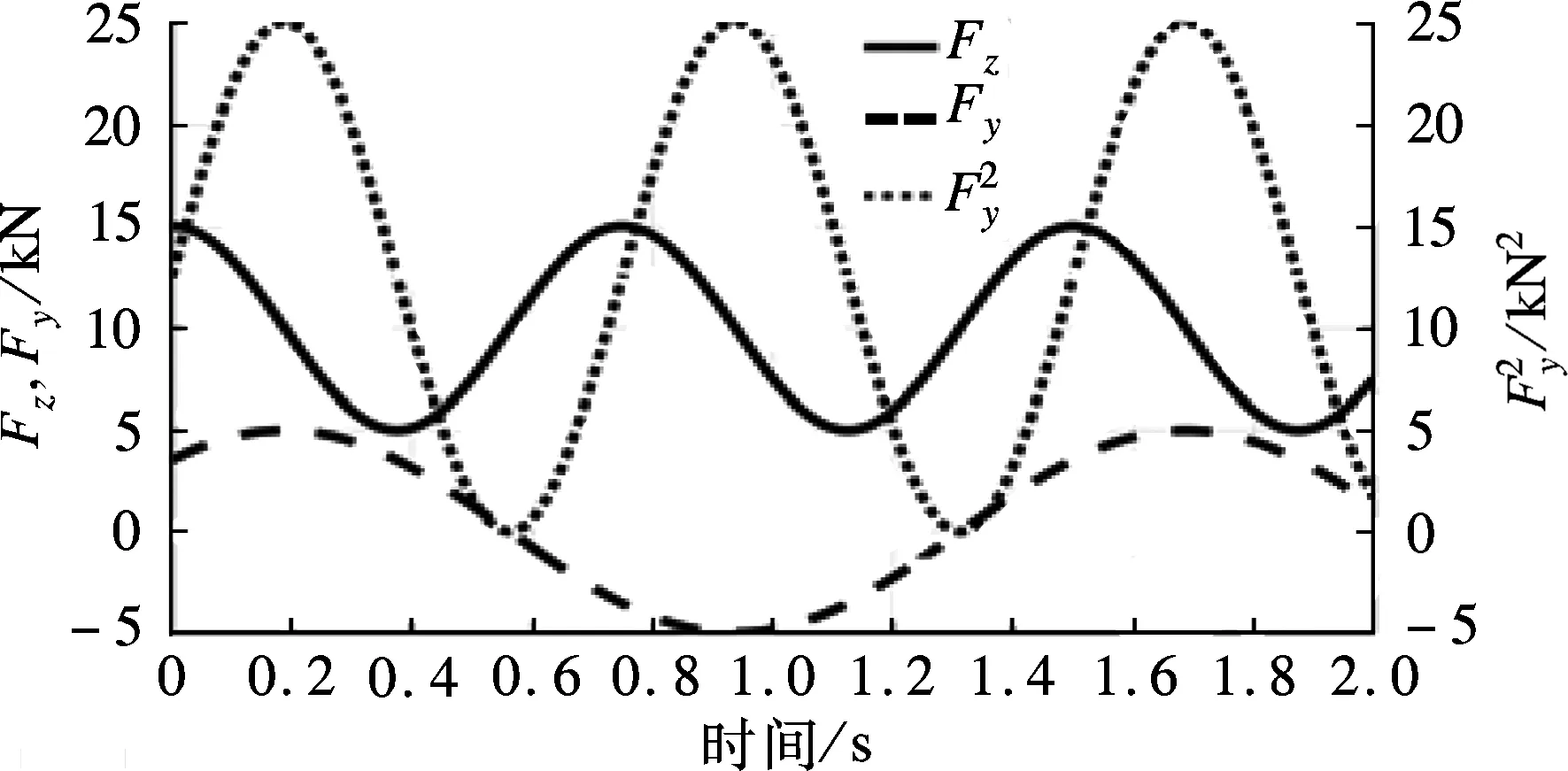
(b) 相位偏移为-90°或90°

(c) 相位偏移为-180°或180°

汽车拖车组合系统的某次典型道路测试数据显示,牵引车后轴动态轴载FzR,1的主导振荡频率1.40 Hz是后轴侧向力FyR,1振荡基波0.67 Hz的一阶谐波[4]．因此,这种谐波效应现象可以认为是CTC系统在谐波响应道路实验中的一种典型现象．

3.2 有效轴载的量化

在单轨模型中,被线性化为常数的车轴侧偏刚度难以准确描述系统动力学特性．Pacejka[12]指出:有效轴侧偏刚度的最终表达中应包含有载荷传递、车身侧倾、转向柔性、侧向力转向、车轮初始外倾角和前束角．在不稳定状态下,瞬态轮载更为复杂．本文针对所考虑的谐波效应,推导出一种包含对谐波效应有显著影响的有效轴载表达式．为了简化相应的理论推导,本文只考虑了对源自非线性谐波效应的主要频率成分(1～2 Hz内)的影响,具体的量化过程见文献[4]．

可以通过基于线性单轨模型的时频域分析方法获得轴侧向力和轴侧偏角的动态幅值．而瞬时轴侧偏刚度是轴侧向力和轴侧偏角的复数值之比,即

(4)

3.3 时频域分析方法

在道路测试中,谐波动态轴载的幅值与相位都是时变的,所以轴侧偏刚度也是时变的．由于车轮侧偏角或轮胎侧偏刚度难以直接获取,因此可以通过选取基于线性单轨模型的方法来求取轴侧偏刚度．本文采用Zhang等[3,13]提出的基于时频域分析的参数识别方法来辨识时变的系统参数,一方面,这种方法本质上与典型的时频域分析方法-短时傅里叶变换[1]相同；另一方面,车辆系统的线性单轨模型也是参数识别方法的一部分．这种基于时频域分析的参数识别方法与有效轴载的量化方法相结合，可以辨识系统的时变参数．该方法的有效性在文献[3,13]中得到了充分的验证．

4 有效轴载对系统动态稳定性的影响

为研究CTC的动态稳定性,在所设计的一系列道路实验中,将系统纵向速度设定为接近动态临界车速,并以一个转向脉冲信号激发系统的临界稳态振荡,即所谓的“车身摆振”．采用基于时频域分析的参数识别方法对实验数据进行分析处理[3],可以发现悬架减震器的谐波效应确实存在并且会影响CTC的有效轴载和轴侧偏刚度．但是仅通过道路实验数据分析无法分离谐波幅值和相位的各自影响,因为悬架减震器的非线性特性无法通过人工方式轻易调整．故本文设计了一种新颖的建模方法以分离谐波幅值和相位的各自影响．

4.1 建模方法

(5)

图4 谐波动态轴载在仿真中的建模方法

采用上述建模方法,在仿真中均能对谐波幅值和相位进行调整．通过合理的调整,可以模拟生成谐波动态轴载,并分别研究轴载谐波力的幅值和相位对系统动态稳定性的影响．

4.2 仿真

通过仿真研究牵引车后车轴轴载谐波力的幅值和相位对CTC系统动态稳定性影响的灵敏度,仿真结果如图5所示．图中,vcrit为系统动态临界速度,CαR,1为轴侧偏刚度,FzR,eff,1为有效谐波动态轴载．

1) 谐波力幅值影响的灵敏度．仿真中设定的增益值相同,在相位偏移为0°,-90°和-180°时谐波动态轴载的幅值也不同．这是因为不同相位偏移下生成的额外谐波力和悬架减震器设计中存在的正常非线性特性引起的谐波力之间的相互作用不同．在3种相位偏移情况下,不同增益值的动态轴载的总谐波力幅值如表1所示．

除了相位偏移-90°的情况外,系统动态临界速度vcrit、轴侧偏刚度Cαr,1、有效谐波动态轴载Fzr,eff,1的变化(见图5(a)、(c)、 (e))与理论预期

表1 不同增益值下的谐波力的幅值 kN

(见图3)均相吻合．对于相位偏移-90°情况,vcrit的急剧减少与Cαr,1的降低相一致,但Fzr,eff,1的减少量偏小,故Cαr,1的降低不完全是由于Fzr,eff,1的减少所引起的,而是与一些元件设计中存在正常非线性特性的影响有关．

2) 谐波力相位影响的灵敏度．由于在频率1.40 Hz 左右处,谐波力幅值也依赖于其相位(也与一些元件设计中存在的正常非线性特性的影响有关),因此分析谐波力相位的影响就相对复杂．在量化的有效轴载Fzr,eff,1中包含有谐波力幅值和相位的信息．从图5(b)、 (d)、(f)可以看出,vcrit,Cαr,1和Fzr,eff,1之间存在较强的依赖关系,当增益值为3.0时,谐波力的幅值随相位变化而改变．

可见,谐波力相位和幅值(在0.2～1.2 kN范围内改变)的变化均会引起vcrit约10 km/h的变化量．这也说明:一方面仿真结果验证了有效轴载的理论分析;另一方面也证明有效轴载的量化方法是有效的．此外,谐波力幅值影响的灵敏度分析结果出现同一幅值对应2个vcrit的问题,主要原因有:① 本文中采用的基于时频域分析的参数识别方法有一定的局限性,短时傅里叶变换仍然需要在最短一个横摆振荡周期内(约为1.5 s)进行,傅里叶变换的平均作用将会掩盖在此时间段内的动态轴载的快速变化,从而引起参数识别误差;② 一些元件设计中存在的正常非线性特性的影响,如悬架弹簧、减震器被设计成在压缩和回弹过程中具有不同的曲线特性,其影响也会叠加到仿真结果中,从而导致相位偏移为0°时同一谐波力幅值对应2个不同的vcrit(见图5(a)),但此叠加影响无法排除．然而,此问题影响较小,仅在相位偏移0°对应的曲线末端与相位偏移-180°对应的曲线始端出现．

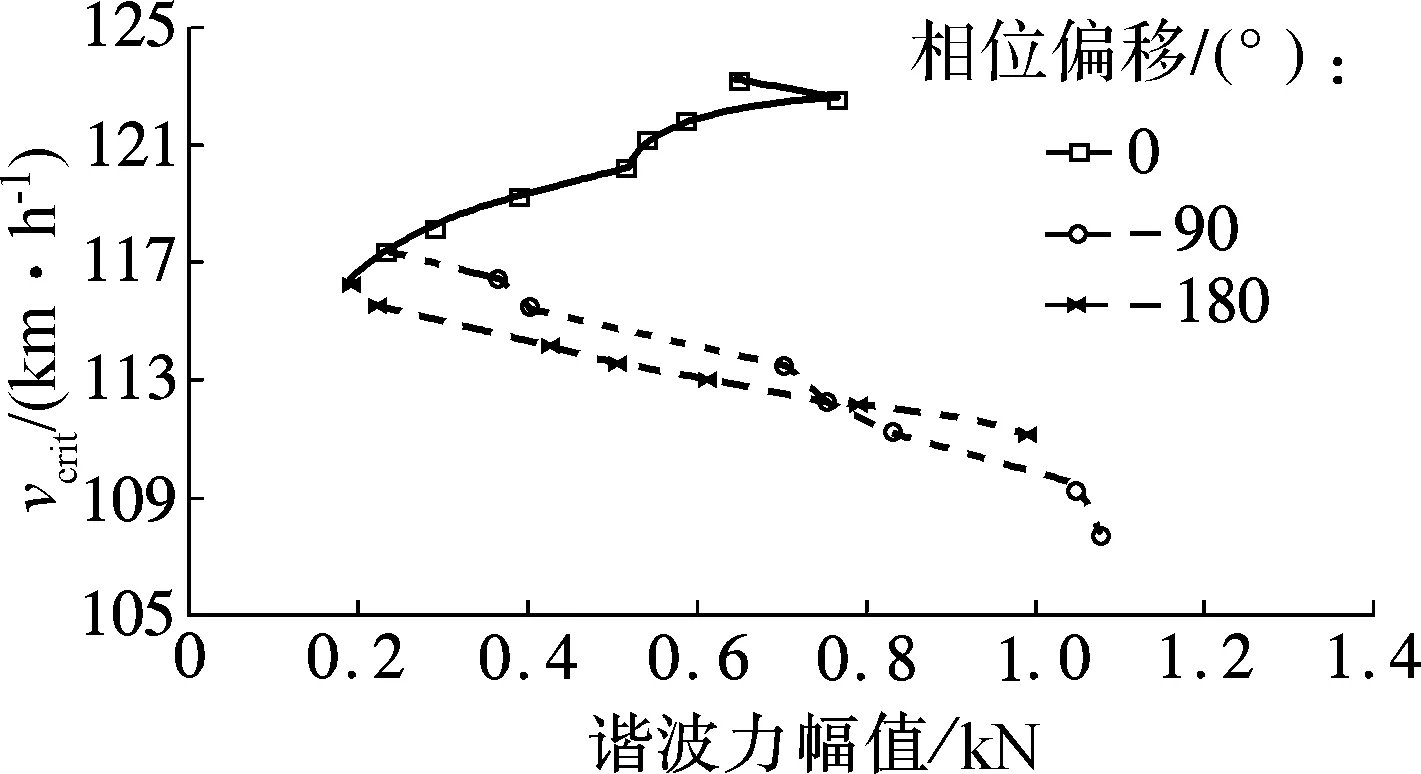
(a) 动态临界速度对幅值影响

(b) 动态临界速度对相位偏移影响

(c) 轴侧偏刚度对幅值影响

(d) 轴侧偏刚度对相位偏移影响

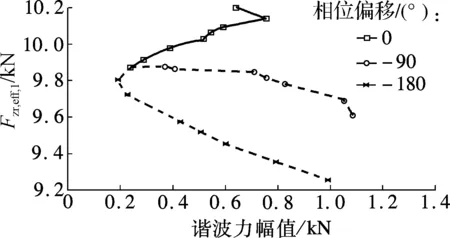
(e) 有效谐波动态轴载对幅值影响

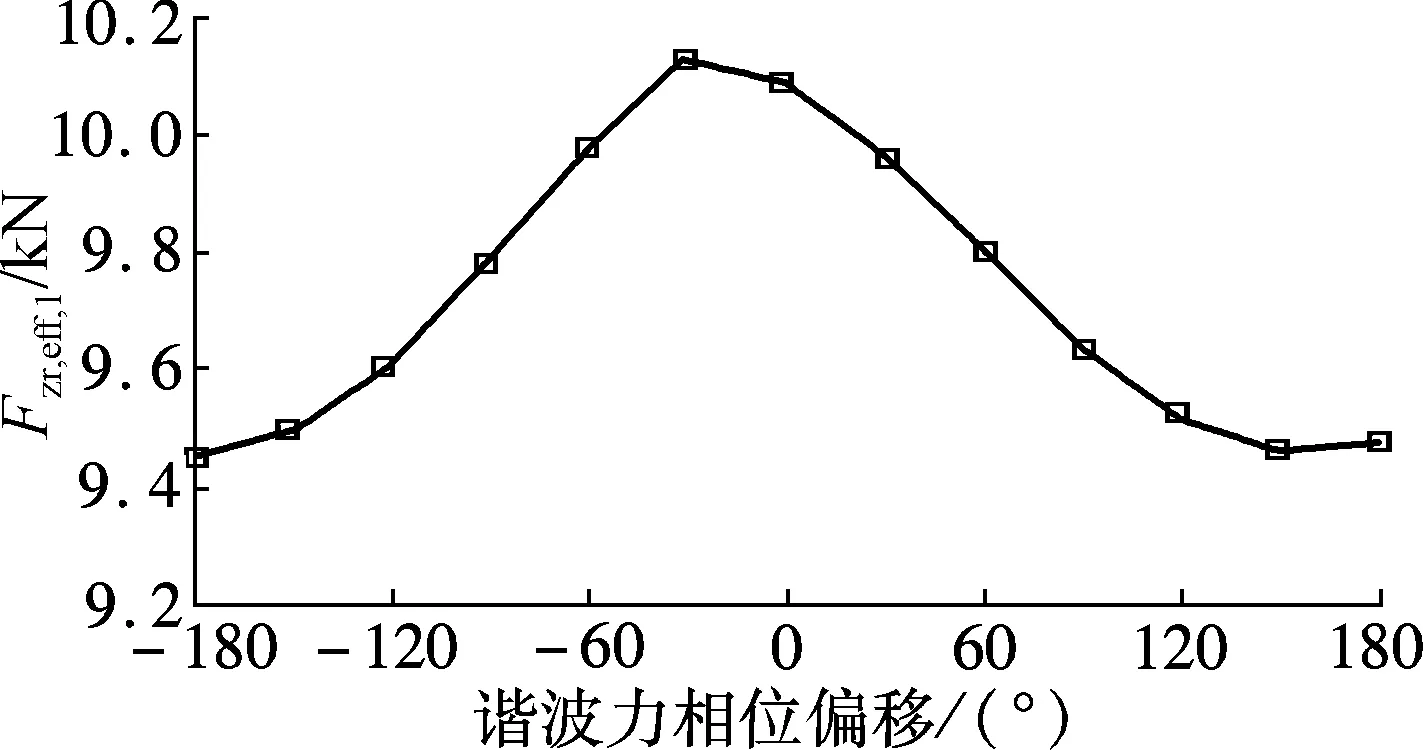
(f) 有效谐波动态轴载对相位偏移影响

5 结语

本文研究了悬架减震器非线性特性对汽车拖车组合系统稳定性的影响,建立了一个含有双轴拖车系统相应的线性单轨模型.在此基础上分析了谐波效应和谐波动态轴载,并对有效轴载进行了量化,采用基于时频域分析的参数识别方法来辨识谐波动态轴载的时变特性．最后,设计了一种基于车辆横摆角速度的建模方法来模拟道路实验中观测到的谐波效应,并通过仿真分析了谐波力幅值和相位对系统动态临界车速的灵敏度．仿真结果表明,谐波力幅值和相位都会引起系统动态临界车速高达约10 km/h的变化量,从而初步验证了本文中考虑的悬架减震器非线性特性引起的谐波动态轴载对汽车拖车组合系统稳定性影响的理论分析．

References)

[1]Qian S.Introductiontotime-frequencyandwavelettransforms[M]. Upper Saddle River, NJ,USA: Prentice Hall, 2002: 90-95.

[2]Hac A, Fulk D, Chen H. Stability and control considerations of vehicle-trailer combination [J].InternationalJournalofPassengerCars-MechanicalSystems, 2008, 1(1): 925-937. DOI: 10.4271/2008-01-1228.

[3]Zhang N, Xiao H,Winner H. A parameter identification method based on time-frequency analysis for time-varying vehicle dynamics [J].ProcIMechEPartD:JournalofAutomobileEngineering, 2016, 230(1): 3-17. DOI: 10.1177/0954407015577908.

[4]Zhang N. Stability investigation of car-trailer combinations based on time-frequency analysis [D]. Darmstadt,Germany:Technische Universität Darmstadt, 2015.

[5]Farjoud A, Ahmadian M, Craft M, et al. Nonlinear modeling and experimental characterization of hydraulic dampers: Effects of shim stack and orifice parameters on damper performance [J].NonlinearDynamics, 2012, 67(2): 1437-1456. DOI: 10.1007/s11071-011-0079-2.

[6]Wang W L, Huang Y, Yang X J, et al. Non-linear parametric modelling of a high-speed rail hydraulic yaw damper with series clearance and stiffness [J].NonlinearDynamics, 2011, 65(1/2): 13-34. DOI: 10.1007/s11071-010-9871-7.

[7]Surace C, Worden K, Tomlinson G R. An improved nonlinear model for an automotive shock absorber [J].NonlinearDynamics, 1992, 3(6): 413-429. DOI: 10.1007/BF00045646.

[8]Dixon J C.Theshockabsorberhandbook[M]. 2nd ed. London, UK： SAE International Inc, 2007:276-277.

[9]Bedük M D, ÇalIkan K, Henze R, et al. Effects of damper failure on vehicle stability [J].ProcIMechEPartD:JournalofAutomobileEngineering, 2013, 227(7): 1024-1039.DOI: 10.1177/0954407012465242.

[10]Wesemeier D, Isermann R. Identification of vehicle parameters using stationary driving maneuvers [J].ControlEngineeringPractice, 2009, 17(12):1426-1431. DOI: 10.1016/j.conengprac.2008.10.008.

[11]Sierra C, Tseng E, Jain A, et al. Cornering stiffness estimation based on vehicle lateral dynamics [J].VehicleSystemDynamics, 2006, 44(1): 24-38. DOI: 10.1080/00423110600867259.

[12]Pacejka H B.Tireandvehicledynamics[M]. 3rd ed. Oxford, UK: Butterworth-Heinemann, 2012:9-12.

[13]Zhang N, Claus S, Wang Y, et al. Analysis methods for time-variant harmonic vehicle dynamics experiments [C]//14thInternationalVDIConference. Hannover, German， 2013:273-286.

[14]ISO. ISO 9815 Road vehicles — Passenger-car and trailer combinations — Lateral stability test [S]. Geneva, Switzerland: International Organization for Standardization,2003.

Effects of nonlinear characteristics of suspension dampers on stability of car-trailer combinations

Zhang Ning Ju Anjian Li Pengcheng Yin Guodong

(School of Mechanical Engineering, Southeast University, Nanjing 211189, China)

To investigate effect on a time-varying harmonic dynamic axle load induced by the change of nonlinear characteristics on suspension dampers installed in the towing car on the dynamic stability of car-trailer combinations, a linear single-track model with a tandem-axle trailer was proposed and an effective axle load was used to quantify the harmonic dynamic axle load. A parameter identification method based on time-frequency analysis was applied in the process, too. Experimental study shows the harmonic effect has a time-varying phenomenon. A simulation method is designed for the purpose of a harmonic force generator to simulate the harmonic effect in road experiments. On this basis, the sensitivity analysis of the influence on the harmonic amplitude or the phase on the system dynamic stability is performed by the simulation. It is preliminarily proved that the proposed theoretical analysis of the harmonic dynamic axle load on the stability effects of car-trailer combinations is reasonable and acceptable.

vehicle dynamics; car-trailer combinations; nonlinear characteristics; time-varying harmonic effect; dynamic stability

10.3969/j.issn.1001-0505.2017.02.009

2016-09-12. 作者简介: 张宁(1985—),男,博士,讲师,nzhang_cn@seu.edu.cn．

国家自然科学基金青年基金资助项目(51605087)、江苏省自然科学基金青年基金资助项目(BK20160671)．

张宁,琚安建,李鹏程，等.悬架减震器非线性特性对汽车拖车组合系统稳定性的影响[J].东南大学学报(自然科学版),2017,47(2):247-253.

10.3969/j.issn.1001-0505.2017.02.009.

U461.6 1

A

1001-0505(2017)02-0247-07