复杂扰动条件下水电站振动传递功率流分析

陶永霞，职保平，刘子祺，马震岳

(1．小流域水利河南省高校工程技术研究中心，河南 开封 475004；2．黄河水利职业技术学院，河南 开封 475004；3．黄河水利水电开发总公司，郑州 450003；4．大连理工大学 建设工程学部，辽宁 大连 116023)

复杂扰动条件下水电站振动传递功率流分析

陶永霞1,2，职保平1,2，刘子祺3，马震岳4

(1．小流域水利河南省高校工程技术研究中心，河南 开封 475004；2．黄河水利职业技术学院，河南 开封 475004；3．黄河水利水电开发总公司，郑州 450003；4．大连理工大学 建设工程学部，辽宁 大连 116023)

为分析水电站实际振动的复杂扰动对结构动力特性分析的影响，在单扰动分析的基础上，结合功率流、Kronecker代数、Hadamard积及随机摄动理论，推导了考虑参数相关和扰动相关的复杂扰动条件下的功率流随机参数结构分析方法，并应用于水电站竖向振动传导分析。通过水电站厂房结构振动分析表明，复杂扰动分析方法的结果是正确的，可分析各参数扰动对能量传导率的灵敏度问题。该研究能够有效降低扰动范围，提高分析的准确率，为准确分析振动传导路径提供保障。

复杂扰动；功率流；随机参数结构；传导路径；水电站

水电站这类巨型复杂结构，各部件生产、安装所导致的材料参数、几何尺寸、边界条件等均存在不确定性(如混凝土等材料参数)，该类不确定性与参数同步存在，属于乘性扰动，而测量所得的参数必然伴随着由噪声干扰(多机工作振动、桥机运行振动干扰等)、测试扰动(环境噪声、仪器噪声等)等引起的加性扰动[1]。水电站振动系统的各参数均富含两类扰动性，属于典型的随机结构问题。结构参数的扰动性可能引起结构动力特性和动力响应的大幅度变化，使力学参数的随机性在一定条件下成为主导因素。

经过近半个世纪的发展，随机参数结构的研究主要发展了Monte-Carlo模拟[2-3]、摄动法[4-6]、随机摄动有限元、随机因子法[7]、区间因子法[8]等，这些方法均将各参数的扰动定义为单一扰动。但实际水电站振动分析时，各参数存在非常复杂的扰动性，针对多扰动情况。目前，复杂扰动量联合分析的随机参数结构研究仅处于探索阶段，而参数及扰动的相关性往往忽略或将其转化为不相关变量的方法进行处理，并不关注相关性对结果的影响。但相关性在特定条件下也可产生非常大的影响，且为精确分析多参数多扰动对结构响应的影响，十分有必要对随着研究的深入， AMBROGIO[9]考虑了加性和乘性扰动之间的相关性，但未涉及参数之间的相关性；HUSAIN等[10]通过加权矩阵形式解决了参数相关性问题，但是该方法仅计算结果进行加权；ZHI等[11]在多扰动摄动分析中考虑参数、扰动之间的相关性，推导了相应的分析方法。

考虑参数扰动性的水电站测试与数值相结合的振动传导分析仅处于探索阶段，国内外仅马震岳团队针对机组-厂房结构进行振动传导分析[12-17]。有必要研究多种传导分析方法进行分析，以功率流为代表的能量传导法在其领域发展迅猛，20世纪70年代后期，用功率流方法评价振动噪声得到广泛认可[18-19]，其中PINNINGTON等[20-21]对功率流的若干研究成果做了系统全面的归纳。目前，功率流理论已在机械振动传导、减振隔振[22-23]、噪声分析与噪声控制等研究领域得到应用，取得显著成果。功率流方法在传导分析中具有明显优势，在多扰动条件下的机组-厂房结构振动传导研究中引入功率流方法能避免高阶矩阵的偏导求解，为多扰动水电机组振动传导的研究提供一种新的分析方法，也能对水电站振动控制提供可相互验证的理论依据。

之前的研究中，作者以摄动法为基础，分析了复杂扰动条件下，摄动法与Monte-Carlo模拟的误差，该研究能为本文提供与随机模拟法的差别，由于分析模型随机参数多达42个，随机模拟法计算量将不可估计，方法不再适用，最终，本文在功率流理论、Kronecker代数、Hadamard积、随机摄动理论等方法的基础上，结合双扰动性及参数之间相关、扰动之间相关性的特点，提出适用于水电机组的复杂扰动功率流分析方法，并进行理论分析和数值计算，给出随机路径的水力振动功率流的一阶矩及二阶矩的数学表达，为研究具有两类参数不确定的水电机组振动能量传导问题提供的依据。

1 振动传递路径系统的功率流方法

功率是指单位时间内作用荷载所做的功即式(1)，其中，Fi和Vi分别代表结构有限域对应的作用荷载和速度分量，可见功率能有效地反映出外荷载和结构响应的组合特征，也能反映出结构的阻抗特性，因此在结构振动传导中，对复杂结构中能量传导路径的识别意义重大。若在时域内对某时间段通过某截面或某区域的功率进行汇总，便可实现对复杂结构功率传导规律的分析。若结构荷载可简化为简谐荷载，其结构速度响应也呈简谐变化，则对某时段某点的功率流计算公式可表达为式(2)。将式(2)中的变量用复向量表示，并进行复数运算，可得式(3)的表达形式，右上角标带有*表示向量的共轭向量。

Pi=Fi·Vi

(1)

(2)

(3)

式中，Pi为T时间段内功率流的有效值，单位W；Fi为简谐荷载，复向量，单位N；Vi为结构某点的响应速度值，复向量，单位m/s；ω为简谐振动的角频率，单位rad/s；φ为速度与荷载的相位角，单位rad。β=V/F即是结构点导纳，1/β即为节点阻抗，可以通过实验的方法测得结构功率流的传导。若荷载激励用一个力功率谱密度来定义的，那么P(ω)就是功率流谱密度。

假设整个机组厂房结构只在水轮机转轮处受竖向简谐激励，如图1所示，且初始相位在整个过程中不发生改变，伞式机组的水电站水力振源的竖向振动可看作位于水轮机处的单振源多路径振动系统，将其简化成多路径的功率流系统，如图2所示。将各个部件分解成隔振系统中的质量单元和隔振单元，即理论上将单元的振动能量分离计算，质量作为刚体单独作用，单元的刚度和阻尼组成隔振单元，此时可利用功率流的相关理论计算得到两条路径的总功率流。由于水电站的机墩部分直接与地基部分相连，并作刚性假设，因此不考虑基础作用。由于各路径内包含多个部件，因此路径内作为多层隔振系统考虑，路径内动力传递关系图如图3所示。

根据功率流四端参数法有：

图1 伞式机组和厂房耦合系统简化模型Fig.1 Simplified model of the umbrella unit

图2 功率流路径示意图Fig. 2 Transfer path of the power flow

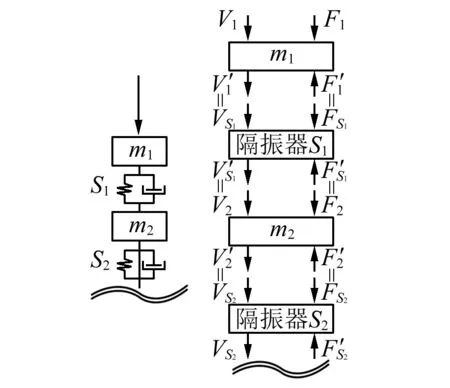
图3 多层隔振系统及动力传递示意图Fig.3 The power transfer path of multi-layer isolation system

(4)

(5)

(6)

(7)

其中，

(8)

(9)

由此可计算各路径功率为：

(10)

(11)

式中，Pzhou，Fzhou，Vzhou分别为通过轴系振动传递至机墩的功率流，力和速度；Pding，Fding，Vding分别为振动通过顶盖系统传递至机墩的功率流，力和速度，至此可得各路径的功率流排序。功率流方法仅关注结构输入输出之间的能量关系，避免了求解整体结构的动力平衡方程，即无需建立结构的整体刚度、阻尼、质量有限元矩阵，大幅度降低了计算时间，提高了工程应用的计算效率，同时功率流方法也具有表征直观等多种优势。

2 基于复杂扰动的功率流路径排序

在水电站结构分析中，刚度、质量、阻尼等参数由于材料性质、制造安装工艺等因素使参数具有乘性扰动性，而通过测试的方法得到相关参数，由于环境噪声和测量噪声的存在，使参数具有加性扰动性；同时由于测试仪器与测量方法的一致性和连续结构离散化的方式得到参数，使参数具有相关性和互相关扰动。

考虑以上情况，将质量、刚度、阻尼描述为一个含n个随机变量的随机向量a，且随机变量同时存在两类扰动量，当各变量的扰动性小于均值的15%时，可将随机变量表示为

(12)

(13)

(14)

Cov(ai,aj)=ρai,ajσaiσaj

(16)

(17)

其中

(18)

忽略二阶以上分量，传递力的扰动量为：

(19)

(20)

(21)

由式(21)可知，传递功率Pi和Pj的协方差函数Cov(Pi,Pj)可用结构随机参数的协方差函数Cov(ak,al)来表示。

(22)

若i=j，则：

(23)

根据Kronecker代数(Vetter 1973)，随机摄动理论和Hadamard积的定义得：

(24)

(25)

将式(25)代入式(24)即可得到各路径传递功率Pi的方差。式(21)只给出了一阶泰勒展开，若取更高阶则精度更高，但会大大增加数学计算的复杂度以及计算量。式(24)表明，在求解传递力方差时，利用随机变量的数字特征直接得到，而样本不参与运算，简化了计算量；同时考虑参数之间相关性时仅在式(24)中进行相应的修正，未对扰动量的计算增加过多的计算量。定义传递率为传递功率的幅值与振源激振力幅值之比：

(26)

若不考虑激振功率P0的扰动性，根据随机变量概率分析的代数综合法，传递率的期望和方差以及传递系数为：

(27a)

(27b)

θ=Eβ/σβ

(27c)

式中，ρ为传递与输入功率流的相关系数。由于服从正态分布的随机变量除以常数时，仍为正态分布。而E[P0]、E[Pi]对于确定系统而言均是可知的，因此传递率的方差仍服从正态分布，传递系数是激振力的传递效率。通过改变激振力的频率即可得到振动路径的传递率在频域内的梯度排序。

上述方法给出了考虑两类扰动量及两类相关性的振动传递路径分析方法，最终给出路径传递率以及传递率的概率特性，在求解过程中只涉及随机参数的一阶灵敏度和随机变量的概率特性，且两个相关系数的引入未过多增加计算量，在简化了计算量的同时提高了计算精度，给解决变异性较小的大体积工程结构的计算问题带来了方便。

3 水电站仿真分析

以某巨型混流立轴伞式水轮发电机组-厂房结构振动传导模型为例，结构如图1所示，不考虑蜗壳及其下部结构影响，假设激励为1.00×106的简谐激励，随机参数均值由水电站施工设计图计算得到，含顶盖系统的振动模型简化过程见文献[17]，各参数均值如下：m1=8.28×104，m2=1.042×106，m3=3.29×105，m4=9.00×105，m5=1.20×105，m6=1.15×105，m7=4.79×106，质量m的单位为kg；k1=7.26×1010，k3=5.72×1010，k4=2.32×1010，k51=2.20×1012，k52=9.41×109，k61=1.73×108，k62=1.73×1010，刚度k单位N/m；c1=5.48×106，c3=4.11×106，c4=1.02×107，c51=2.57×107，c52=7.51×105，c61=2.23×105，c62=9.99×104，阻尼c的单位为N·s/m；各参数含两个服从正态分布的扰动量，其中乘性扰动量与参数获取的难易程度有关，即：包含推力轴承的竖向刚度k51和顶盖与转轮之间的密封等效竖向刚度k61乘性方差系数为0.15；顶盖上承载的控制部件等附加部件较多，使不确定因素较多，取等效弯曲刚度k62的乘性方差系数为0.1；其余参数的乘性方差系数为0.05。加性随机量中包含环境噪声和测量噪声，随机量幅度往往与测量量程有关，假定各参数可测，以各参数的均值确定参数量程，以测试量程为扰动量取值依据，分别取质量的加性扰动的方差为104和刚度的加性扰动的方差为108。

图4、图5给出不同计算方法下，轴系路径的传递率期望和方差，其中“不相关”为不考虑两类相关性的算法；“扰动相关”为只考虑扰动量之间相关性的算法(采用Vetter, 1973所用计算方法)；“参数相关”为只考虑参数之间具有相关性的算法(与方法2类似)；“两类相关”为同时考虑两类相关性的算法，即由式(24)计算所得的结果。图4、图5中分别给出了400-405 rad/s的局部放大特性曲线。

图4和图5表明：①同时考虑两类相关性的方法相较于其他方法所得方差范围最小，由此可得出考虑两类相关性的方法在具有理论支持的情况下，显著的缩小了扰动性范围，其中考虑两类相关性的计算中，期望降低了18.09%，方差降低了99.78%;②扰动量之间的相关性有助于减小期望范围，降幅51.05%，但方差不显著仅降低0.41%，这种现象的产生推测是由于加性扰动量与乘性扰动量的差异较大，使相关系数对扰动量范围修正作用减小造成的；③参数间所具有的相关性对方法范围的减小产生明显的优化作用，参数间相关系数仅0.002 3时，期望降幅59.75%，方差降幅99.78%。

图4 各方法计算轴系传导功率期望值Fig. 4 Expectation of the shaft transmissibility in the frequency domain by different methods

图5 各方法计算轴系传导功率方差值Fig. 5 Variance of the shaft transmissibility in the frequency domain by different methods

图4和图5表明：在结构分析中，分析期望(均值)时需考虑扰动相关性，分析方差时需考虑参数相关性，以往忽略相关性对精确分析十分不利。

图6给出考虑两类相关性的竖向振动路径功率传递率的期望排序，图7给出方差排序。轴系统传递率期望与方差均大于顶盖系统，轴系统与顶盖系统的传递能量比比为142 862：1，轴系统与顶盖系统的传递率期望比为213 399：1；相较于随机摄动法计算的传递率而言[23]，两条路径传递比约为摄动法计算结果的平方，这是由于功率流由力和速度构成，而传递力并不考虑速度的因素，因此，结果也将引入速度的倍数关系。图6、7表明顶盖系统传递率远小于轴系统，印证了传统分析忽略顶盖系统的可行性，同时也与实际工程中并未出现顶盖系统振动过大这一现象向吻合，但为精确分析结构振动形态、振动分布、以及区分振动传递路径、复杂结构可靠度等时，考虑顶盖系统是有必要的。

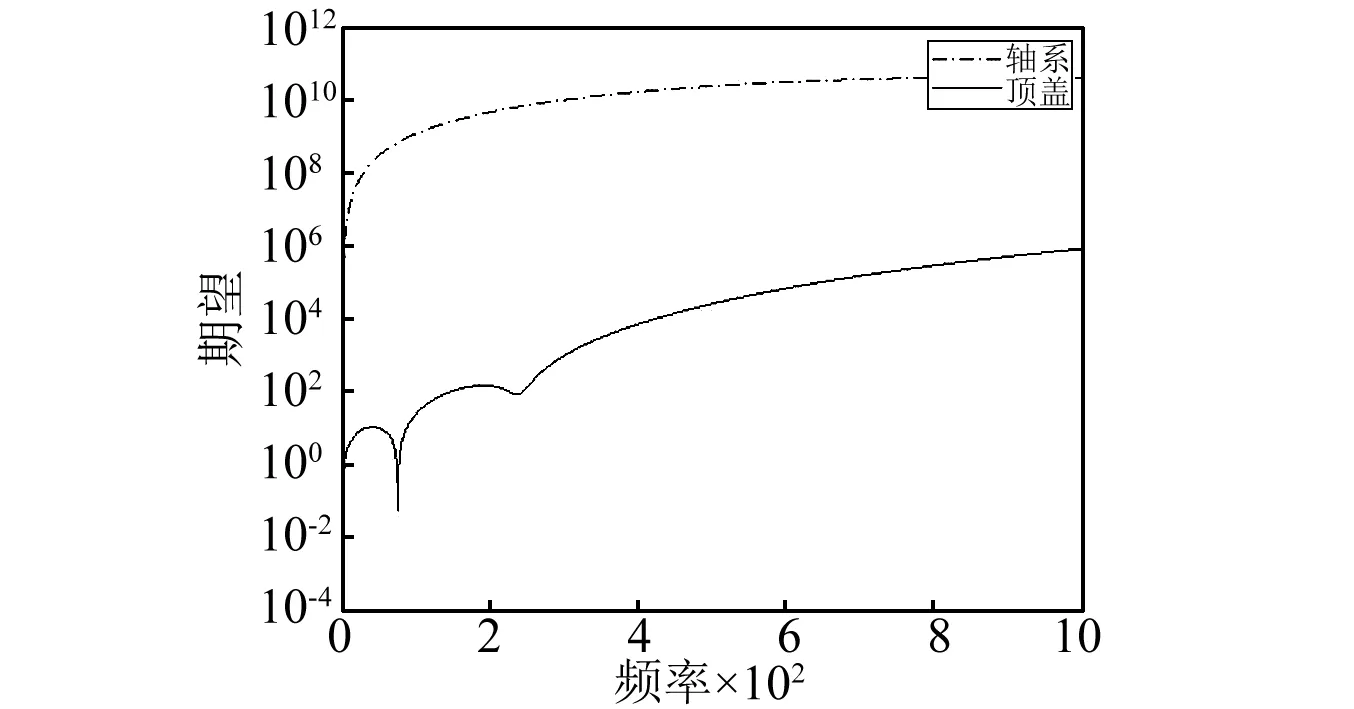
图6 考虑两类相关性的各路径传递率期望值Fig. 6 Expectation of paths transmissibility with two type relevance

图7 考虑两类相关性的各路径传递率方差值Fig. 7 Variance of paths transmissibility with two type relevance

4 结 论

实际测试环境中，扰动成分十分复杂，干扰源也不能完全确定，用单扰动量进行分析存在局限性，因此，在作者之前研究的基础上，本文进一步推导了考虑两类相关性的功率流随机参数结构分析方法，并将其应用于水电站竖向振动传导分析，其研究不仅仅完善了随机参数结构振动分析方法，并为研究多扰动条件下水电站振动传导问题提供了新的思路，本文主要得到以下结论：

(1) 利用功率流理论、Kronecker代数、Hadamard积、随机摄动理论等方法，推导考虑两类相关性的功率流随机参数分析方法，得到可用于多扰动能量传导的传递能量、传递率及其数学特征值等问题的解析计算方法。

(2) 伞式水轮发电机组轴系统和厂房结构的动力学分析结果表明相关系数对扰动性范围的影响较大，其中分析期望时，必须考虑扰动之间的相关性，分析方差时必须考虑参数之间的相关性。

(3) 伞式机组-厂房结构竖向振动传导分析中，轴系统传递率远大于顶盖系统，传统分析中，忽略顶盖系统是可行的，但在进一步精确分析时，有必要考虑顶盖系统对整个机组-厂房耦合结构振动的影响。

水电站机组与厂房的振动传递路径是一个复杂的过程，通过对水电站竖向振动模型在频域内传递功率的灵敏度以及功率的传递率分析可以清晰的了解竖向振动中各传递路径的贡献度，为研究整个水电站机组厂房的传递路径打下基础。

[ 1 ] 职保平. 基于复杂扰动的水电机组与厂房振动传导研究[D]. 大连: 大连理工大学, 2014.

[ 2 ] SINGH B N, YADAV D, IYENGAR N G R. Natural Frequencies of composite plates with random material properties using higher-order shear deformation theory [J]. International Journal of Mechanical Sciences, 2001, 43: 2193-2214.

[ 3 ] POPESCU T D. Detection and diagnosis of model parameter and noise variance changes with application in seismic signal processing [J]. Mechanical Systems ﹠ Signal Processing, 2011, 25(5): 1598-1616.

[ 4 ] KAPLUNOV J D, NOLDE E V, SHORR B F. A perturbation approach for evaluating natural frequencies of moderately thick elliptic plates [J]. Journal of Sound and Vibration, 2005, 281(3/4/5): 905-919.

[ 6 ] MADANI M, FATHIZADEH M, KHAN Y, et al. On the coupling of the homotopy perturbation method and Laplace transformation [J]. Mathematical and Computer Modelling, 2011, 53(9/10): 1937-1945.

[ 7 ] MA J, GAO W, WRIGGERS P. The analyses of dynamic response and reliability of fuzzy-random truss under stationary stochastic excitation [J]. Computational Mechanics, 2010, 45(5): 443-455.

[ 8 ] GAO W, SONG C M, TIN-LOI F. Probabilistic interval response and reliability analysis of structures with a mixture of random and interval properties [J]. Computer Modeling in Engineering ﹠ Science, 2009, 46(2): 151-189.

[ 9 ] AMBROGIO E G D. The dynamics of complex stochastic models evolution of a correlation function with random fluctuations [J]. Mathematical and Computer Modelling, 1998, 28(3):15-20.

[10] HUSAIN N A, KHODAPARAST H H, OUYANG H. Parameter selection and stochastic model updating using perturbation methods with parameter weighting matrix assignment [J]. Mechanical Systems and Signal Processing, 2012, 32: 135-152.

[11] ZHI B P, MA Z Y. Path transmissibility analysis considering two types of correlations in hydropower stations [J]. Journal of Applied Mathematics, 2013:802546.

[12] ZHI B P, MA Z Y. Disturbance analysis of hydropower station vertical vibration dynamic characteristics: the effect of dual disturbances [J]. Structural Engineering and Mechanics, 2015, 53(2): 297-309.

[13] 马震岳, 董毓新. 水电站机组及厂房振动的研究与治理 [M]. 北京: 中国水利水电出版社, 2004: 34-35.

[14] 马震岳, 董毓新. 水轮发电机组动力学 [M]. 大连:大连理工出版社. 2003: 197-199.

[15] 徐伟, 马震岳, 职保平. 基于功率流理论的大型水电站厂房结构脉动压力频响分析[J]. 水利学报, 2012(5):615-622. XU Wei, MA Zhenyue, ZHI Baoping. Analysis on frequency response to pulsating pressure in large hydropower house based on the theory of power flow [J]. ShuiLi Xuebao, 2012(5):615-622.

[16] 徐伟, 马震岳, 职保平. 水压脉动能量传导对水电站厂房墙体影响分析[J]. 水力发电学报, 2013, 32(2): 233-239. XU Wei, MA Zhenyue, ZHI Baoping. Analysis on power flow transmission of pressure fluctuation along the walls of hydropower house [J]. Journal of Hydroelectric Engineering, 2013, 32(2): 233-239.

[17] 职保平, 马震岳, 吴嵌嵌. 考虑顶盖系统的水轮机竖向振动传递路径分析[J]. 水力发电学报, 2013, 32(3): 241-246. ZHI Baoping, MA Zhenyue，WU Qianqian. Study on transfer paths of vertical vibrations in the head cover system of turbine [J]. Journal of Hydroelectric Engineering, 2013, 32(3): 241-246.

[18] GOYDER H G D. Vibration power flow partⅠandⅡ [J]. Journal of Sound and Vibration, 1980, 68: 59-75.

[19] WOHLEVER J L, BEMHARD R J. Mechanical energy flow models of rods and beams [J]. Journal of Sound and Vibration, 1992,153(1).153:1-19.

[20] PINNINGTON R J, WHITE R G. Power flow through isolators to resonant and nonresonant beams [J].Journal of Sound and Vibration, 1981, 75(2):179-197.

[21] PINNINGTON G R. Vibrational power transmission from finite source beam to an infinite receiver beam via a continuous mount [J]. Journal of Sound and Vibration, 1990,137(1):117-129.

[22] 殷学文, 崔宏飞, 顾晓军,等. 功率流理论、统计能量分析和能量有限元法之间的关联性 [J]. 船舶力学, 2007, 11(4): 637-646. YIN Xuewen, CUI Hongfei, GU Xiaojun, et al. Relevancy among power flow theory, statistical energy analysis and energy finite element method [J]. Journal of Ship Mechanics, 2007, 11(4): 637-646.

[23] 赵群, 张义民, 赵晋芳. 频域内振动路径的功率流传递度排序 [J]. 航空动力学报, 2009(5): 1177-1181. ZHAO Qun, ZHANG Yimin, ZHAO Jinfang. Powerflow transfer ratio of vibration path systems in frequency range [J]. Journal of Aerospace Power, 2009(5): 1177-1181.

Power flow transmissibility analysis considering complex disturbances in hydropower stations

TAO Yongxia1,2, ZHI Baoping1,2, LIU Ziqi3, MA Zhenyue4

(1 .Engineering Technology Research Center of Small Watershed Conservancy University of Henan Province, Kaifeng 475004，China;2 .Yellow River Conservancy Technical Institute, Kaifeng 475004，China;3.Yellow River Water Conservancy and Hydropower Development Corporation, Zhengzhou 450003，China;4. Faculty of Infrastructure Engineering, Dalian University of Technology, Dalian 116023，China)

The effects of structural parameter disturbances on the dynamic characteristics of an actual hydropower station powerhouse were analysed. The power flow analysis method considering complex disturbances and parameter-related disturbances were focused. On the basis of single disturbance analysis, the stochastic perturbation method was expanded and integratedly used with the dual disturbances analysis, power flow analysis, Kronecker algebra and Hadamard product. The correctness and feasibility of the method were validated by an example of analyzing the vibration model of the hydropower station powerhouse. The results indicate that the method proposed can efficiently reduce the disturbance range and can accurately analyze the transfer paths of vertical vibration in hydropower stations.

complex disturbance; power flow; stochastic perturbation method; transfer path; hydropower station

国家自然科学基金资助(51379030)

2015-08-05 修改稿收到日期： 2016-01-20

陶永霞 女，硕士生，副教授，1971年12月生

职保平 男，博士生，讲师，1983年9月生

E-mail:clownzhi@hotmail.com

TV731

A

10.13465/j.cnki.jvs.2017.06.015