泡沫填充多边形单锥管与双锥管斜向加载下耐撞性分析

陈亚枫, 白中浩

(湖南大学 汽车车身先进设计制造国家重点实验室，长沙　410082)

泡沫填充多边形单锥管与双锥管斜向加载下耐撞性分析

陈亚枫, 白中浩

(湖南大学 汽车车身先进设计制造国家重点实验室，长沙410082)

锥形泡沫填充结构结合了泡沫填充结构与锥形结构的优势，具有优异的吸能性和抵抗失稳变形的能力。研究了具有不同横截面的泡沫填充多边形单锥管(FSPTTs)与泡沫填充多边形双锥管(FBPTTs)在四种冲击角度下的耐撞性。采用多准则评估方法(COPRAS)对不同横截面的泡沫填充单锥管与泡沫填充双锥管的综合耐撞性进行了评估。评估表明：综合考虑多种冲击角度时，圆形截面泡沫填充单锥管较其他截面泡沫填充单锥管具有更好的耐撞性；圆形截面泡沫填充双锥管较其他截面泡沫填充双锥管具有更好的耐撞性。最后，针对圆形截面泡沫填充单锥管与圆形截面泡沫填充双锥管，以最大比吸能和最小峰值力为目标，采用非支配遗传算法对这两种结构在四种冲击角度下进行了多目标优化。结果表明：当冲击角度从0°变化到10°时，两种结构的Pareto曲线变化不大，而当冲击角度从10°变化到30°时，冲击角度对Pareto曲线形状和位置有显著影响；在冲击角度为0°和10°时，圆形截面泡沫填充双锥管的耐撞性优于圆形截面泡沫填充单锥管，而在冲击角度为20°和30°时，圆形截面泡沫填充单锥管的耐撞性优于圆形截面泡沫填充双锥管。实际应用中，可以根据工程需要选择合适的结构。

泡沫填充；耐撞性；锥形结构；斜向加载；多目标优化

由于具有优异的吸能性和较轻的重量，泡沫填充薄壁结构作为吸能装置被广泛应用于汽车、航天等领域。研究人员采用实验、数值模拟和理论推导的方法对泡沫填充薄壁结构的吸能特性进行了大量的研究[1-2]。这些研究表明，除了泡沫本身具有极好的能量吸收能力外，其和管壁之间的交互作用进一步增强了结构整体的能量吸收能力。

实际生活中，吸能结构可能受到多方向的冲击载荷的作用。HAN等[3]研究发现，加载角度可直接影响到方管的变形模式，且存在一个临界加载角度，使得变形模式从渐进压溃转向侧向弯曲模式。REYES等[4-6]进一步研究发现，不管是填充还是未填充泡沫的方管，其吸能特性均随着变形模式从渐进压溃转变为侧向弯曲而明显降低。因此，研究斜向冲击载荷下的薄壁管变形模式及吸能特性对提高车辆偏置碰撞和斜角碰撞条件下的安全性有重要的意义。

与直管相比，锥形薄壁结构在受到轴向冲击时具有更稳定的力-变形响应和更低的峰值力[7]，而且在斜碰撞中发生失稳变形的概率较低[8-10]。为结合锥形结构与泡沫填充结构的优势，研究人员对泡沫填充锥形薄壁结构展开了研究。AHMAD等[11- 12]研究了圆形截面泡沫填充锥形管在受到轴向与斜向负载时的耐撞性，其研究发现，在受到轴向冲击力时，泡沫填充锥形管较中空管具有更好的吸能性、更高的压溃加载效率和更稳定的变形模式；在受到斜向负载时，泡沫填充锥形管发生失稳变形时的临界角度大于中空管发生失稳变形时的临界角度，而且泡沫填充锥形管在失稳变形时的吸能性也优于中空管在失稳变形时的吸能性。ZHANG等[13]研究了圆形截面泡沫填充锥形管在多种负载下的耐撞性，其研究表明在综合考虑多种负载时，泡沫填充管的耐撞性要优于中空管。HOU等[14]对圆形截面泡沫填充锥形管在轴向负载下进行了多目标优化，并与圆形截面中空单锥管和双锥管进行了比较，其研究发现，泡沫填充锥形管的耐撞性要优于中空单锥管和双锥管。

上述研究都是针对横截面为圆形或者方形的泡沫填充单锥管，暂无横截面为其他多边形的泡沫填充单锥管的研究。此外，研究发现泡沫填充双直管较泡沫填充单直管在轴向负载下具有更优的耐撞性[15-16]，但是暂无关于泡沫填充双锥管的研究，尤其在斜碰撞工况下的研究。为此，本文综合研究了具有不同横截面的泡沫填充多边形单锥管(FSPTTs)与泡沫填充多边形双锥管(FBPTTs)在四种冲击角度下的耐撞性。通过赋予不同耐撞性评价指标权重因子，采用多准则评定方法选择出综合耐撞性最优的FSPTTs与FBPTTs，结果表明圆形截面泡沫填充单锥管较其他FSPTTs具有更优的综合耐撞性，圆形截面泡沫填充双锥管也较其他FBPTTs具有更优的综合耐撞性。最后，针对圆形截面泡沫填充单锥管与圆形截面泡沫填充双锥管，以最大比吸能和最小峰值力为目标，以泡沫密度、壁厚和锥角为优化变量，结合Kriging模型和非支配遗传算法对两种结构在四种冲击角度下进行了多目标优化，并比较分析了两种结构在优化后的耐撞性。

1　材料与方法

1.1结构耐撞性评估准则

一般来说，评价结构耐撞性指标有吸能量(EA)、比吸能(SEA)、平均冲击力(MCF)、冲击峰值力(PCF)和压溃加载效率(CLE)等[17]。吸能量EA表示结构产生塑性变形后吸收的能量，其值可以通过对力-位移曲线积分得到[18]，即：

(1)

式中：d为结构的有效变形量；F(x)为瞬间冲击力。对于给定的变形距离d，平均冲击力(MCF)可以表示为

(2)

作为吸能装置，一般希望结构具有较高的压溃加载效率(CLE)。压溃加载效率(CLE)定义为平均冲击力与峰值力的比值：

(3)

式中：PCF为冲击峰值力。

比吸能SEA是评价一个结构的能量吸收效率的指标，用来描述结构单位质量吸收的冲击能量，可表示为

(4)式中，M为结构的总质量。显然，SEA越高，吸能性越好。

1.2泡沫填充双锥管与单锥管几何描述

为探究FSPTTs与FBPTTs的耐撞性，本文考虑了横截面为四边形、六边形、八边形和圆形的泡沫填充单锥管(如图1(a))与双锥管(如图1(b))。FSPTTs底部横截面外接圆直径(Db)与顶部横截面外接圆直径Dt分别为80 mm和40 mm，管的长度L为200 mm。该几何尺寸源自一般乘用车前纵梁尺寸[19]。对于FBPTTs，内管底部横截面外接圆直径Dbi为外管底部横截面外接圆直径Db的一半，内管顶部横截面外接圆直径Dti为外管顶部横截面外接圆直径Dt的一半，厚度和外管一致。

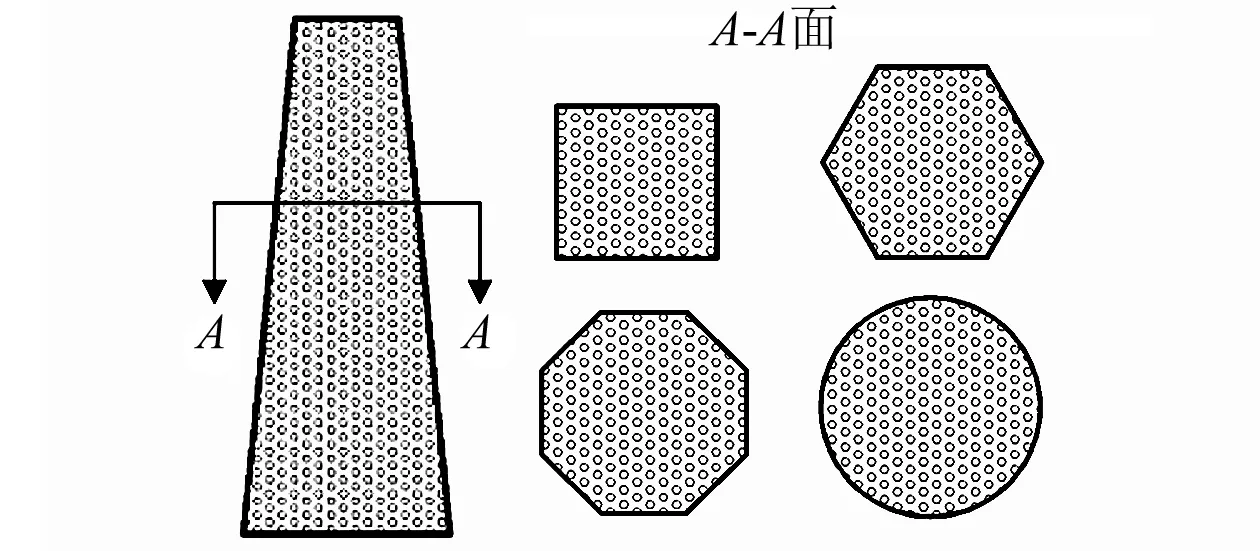
(a) 泡沫填充单锥管

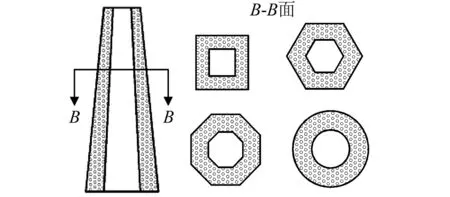
(b)泡沫填充双锥管

1.3材料属性

外管采用材料为AA6060 T4，材料参数为：密度ρ=2.7×103kg/m3，杨氏模量E=68.2 GPa，初始屈服应力σy=80 MPa，极限应力σu=173 MPa，泊松比μ=0.3，幂律指数n= 0.23[20]。拉伸应力应变曲线如图2所示。本构模型采用考虑应变强化的分段线弹塑性模型，由于铝合金为应变率非敏感材料，模型中忽略其应变率效应[21]。

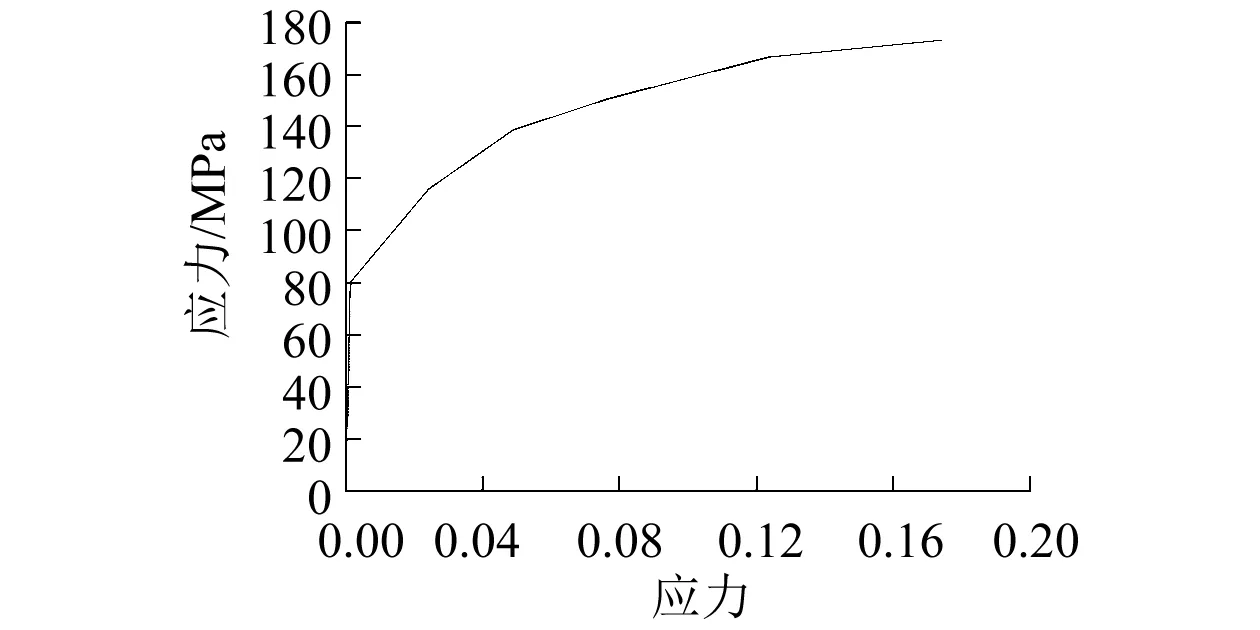
图2　AA6060 T4应力-应变曲线Fig.2　Tensile stress-strain curve of AA6060 T4

泡沫铝材料本构模型采用Deshpande and Fleck建立的各向同性材料模型[22]，该模型中材料的屈服准则定义为

φ=σe-Y≤0

(5)

式中：φ表示屈服面；Y为屈服应力；σe为特征应力，表示为

(6)

式中：σv与σm分别为等效应力和平均应力；α为决定屈服面形状的参数，可以表示为

(7)

式中：vp为塑性收缩系数，对于铝泡沫，vp一般为1，计算得到α=2.12。该模型还采用了应变强化准则

(8)

式中：εe为等效应变；σp，α2，γ，β和εD为材料参数，可以表示为密度的函数

(9)

式中：ρf和ρf0分别为泡沫密度和基体材料密度；C0，C1和ψ为常数，如表1所示。由式(9)可以看出泡沫弹性模量也是关于密度的函数。

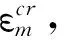
1.4有限元模型

本节以横截面为方形的泡沫填充单锥管为代表描述有限元模型的建立(如图3所示)。外管采用Belyschko-Tsay四节点壳单元建模，壳单元沿厚度方向取3个积分点。泡沫铝采用8点实体单元模拟，包含1点缩减积分。管与刚性墙之间采用自动点-面接触，泡沫铝与外管之间采用自动面-面接触。另外，为避免产生穿透，对外管应用自动单面接触。所有接触的静态与动态摩擦因子分别为0.2和0.3。仿真中管的下端固定，质量为600 kg的刚性墙以15 m/s的初速度冲击管的上端。

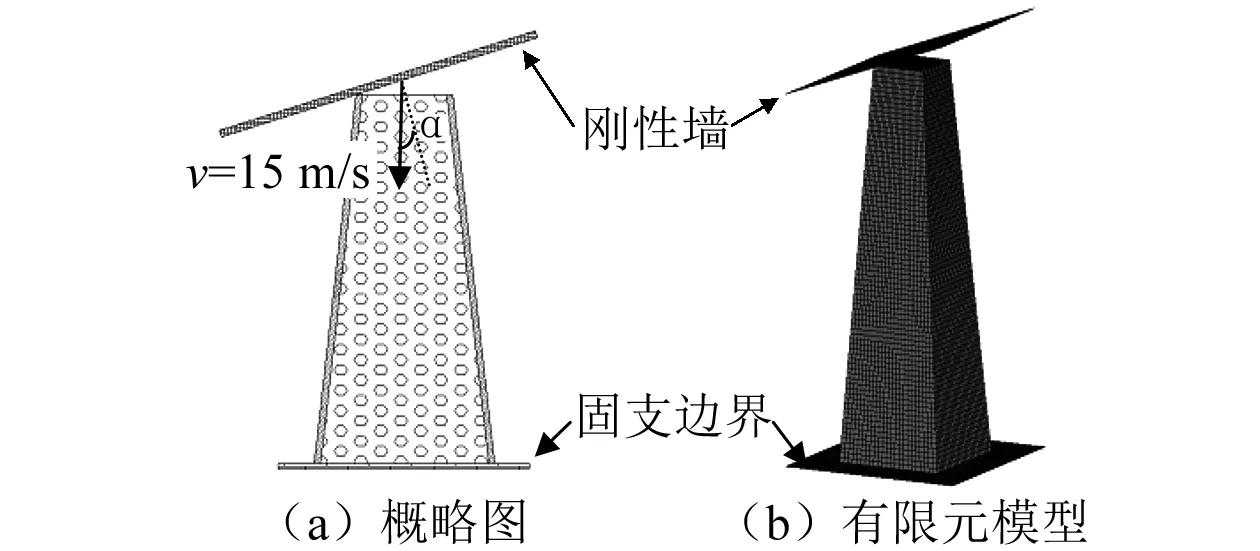
图3　泡沫填充单锥管有限元模型Fig.3 3D finite element modeling of foam-filled single taper tube

1.5多准则评估方法

综合考虑多个耐撞性指标评定结构的耐撞性能属于多准则决定问题，本文选用CHATTERJEE等[26]提出的多准则评估方法 (COPRAS) 对结构的综合耐撞性进行评估。该方法综合考虑了多种评价指标及相应的权重因子，通过考虑各个指标重要性对候选项进行逐步评估与排名。 COPRAS的评估步骤如下：

步骤 1 定义初始决策矩阵X

(10)

式中：xij表示ith候选项关于jth评估准则的性能值;m为候选项的个数；n为评估准则的个数。

步骤 2 采用式(11)对矩阵进行名义化，以获得各准则的无量纲值，便于比较。

(11)

步骤 3 确定加权名义化矩阵D

(12)

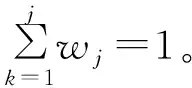
步骤 4 采用式(13)和式(14)确定ith候选项代表有利属性和不利属性的加权名义值之和。有利属性越高(例如SEA)、不利属性越低(例如PCF)则性能越优。

(13)

(14)

式中：p，q分别为评价指标中有利属性与不利属性的个数。各S+i之和与S-i之和应分别等于代表有利属性与不利属性的评估指标加权值之和。S+i之和与S-i之和可以表示为

(15)

(16)

步骤 5 通过式(17)计算各候选项的相对重要性值，相对重要性值越大说明候选项的综合性能越好。

(17)

式中：S-min为S-i的最小值。

步骤 6 根据式(18)计算各候选项定量效用值 (Ui)，Ui和Qi值直接相关，Ui为100%的项即为综合性能最佳的候选项。

(18)

式中：Qmax为各候选项Qi的最大值。

2　数值仿真结果与讨论

2.1有限元模型验证

HANSSEN等[27]通过大量实验，建立了方形截面泡沫填充直管平均压缩力(MCF)的理论公式。泡沫填充锥管可以看成泡沫填充直管的一种特殊形式，本文通过对比泡沫填充直管MCF仿真值与理论值对模型进行验证。 MIRFENDERESKI 等[28-29]也采用相同的方式验证了方形截面或圆形截面的泡沫填充锥管有限元模型。

方形截面泡沫填充直管在动态压缩时平均压缩力理论公式可以表示为

(19)

式中：σ0,t,bm,ρ0分别为外管的特征应力, 壁厚,边长和材料密度；v0为刚性墙初始速度；σf,Af,At分别为泡沫平台应力, 泡沫面积, 外管面积;Cavg为泡沫与外壁的交互系数，与变形量相关，本文为6.48;Cine为动态放大系数,是基于式(20)[30]的函数，如图4所示。

(20)

本文Cine为0.66。

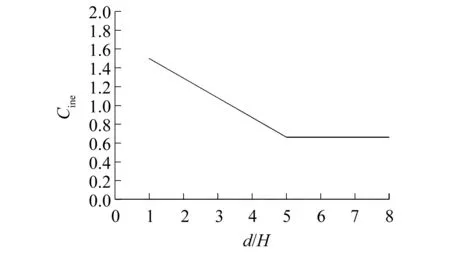
图4　Cine与d/H的关系Fig.4 The relationship of Cine and d/H

泡沫填充直管MCF仿真值关于距离的变化曲线与理论值的比较如图5所示，可知仿真值与理论值拟合较好。因此，可以将本仿真方法扩展到泡沫填充多边形单锥管与泡沫填充多边形双锥管仿真模型的建立。

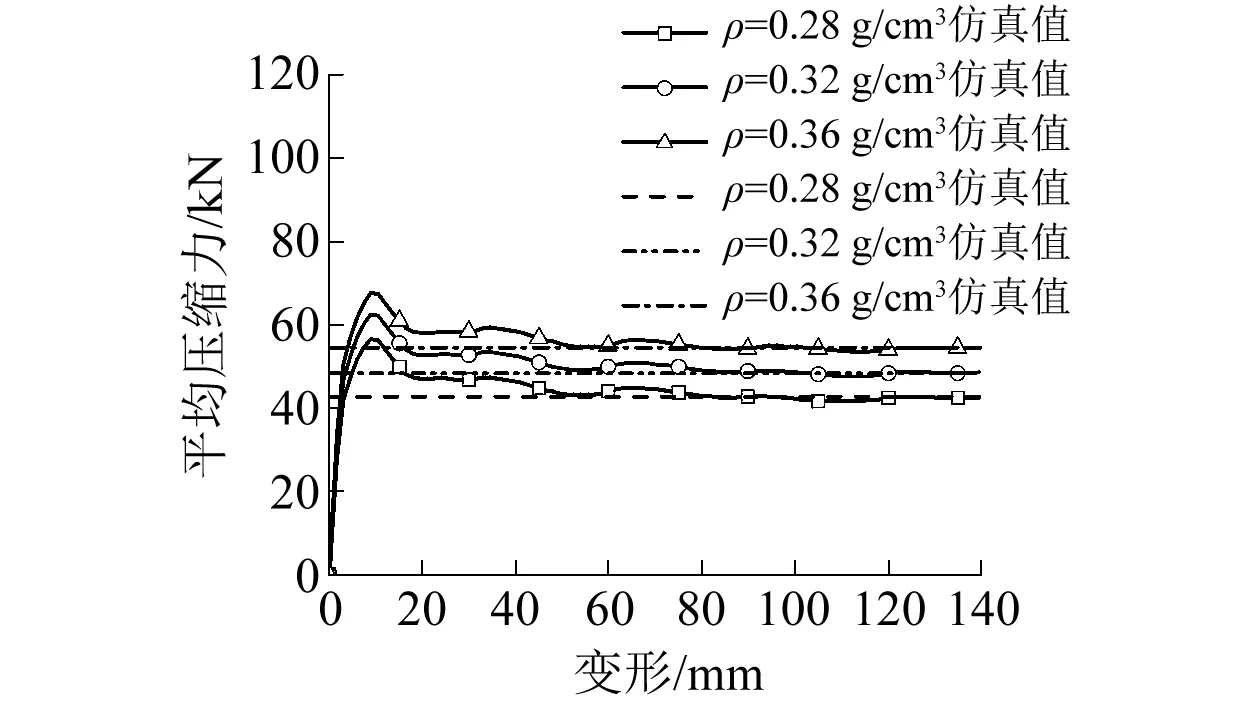
图5　方形截面泡沫填充单锥管平均力-位移曲线Fig.5 Mean crushing force versus deflection for foam-filled square tubes

2.2斜向加载下FSPTTs与FBPTTs耐撞性比较分析

现实中保险杠最大可能会受到与纵轴方向呈30°的冲击负载[31]，本文通过改变刚性墙与薄壁管之间的夹角(定义为α，如图3所示)，使α在0°(0°为薄壁管垂直于刚性墙)，10°，20°以及30°的情况下，研究冲击角度对结构耐撞性的影响，初始冲击速度均为15 m/s。FSPTTs和FBPTTs各耐撞性评价指标如表2所示，表中F代表泡沫填充、S代表单锥管、B代表双锥管、P代表多边形、数字代表横截面边数、C代表横截面为圆形，例如FSP4代表横截面为四边形的泡沫填充单锥管，FBPC代表横截面为圆形的泡沫填充双锥管。由表2可知，在相同加载角度下，FSPTTs和FBPTTs的吸能量(EA)与平均冲击力(MCF)基本上随着横截面边数的增加逐渐上升。为综合考虑各耐撞性指标，本文采用COPARS评估方法对FSPTTs和FBPTTs的耐撞性进行评估与排名。由于EA和MCF名义化后具有相同的值，因此本文选用的评估指标为PCF、MCF、SEA、CLE，不包含EA。各耐撞性指标权重因子选择为：ωPCF=1/6,ωSEA=1/3,ωMCF=1/3,ωCLE=1/6。首先根据式(11)和(12)对表2中用于评估的各耐撞性指标值进行加权名义化，FSPTTs和FBPTTs各耐撞性指标名义化结果分别如表3和表4中NPCF、NSEA、NMCF、NCLE所示。然后根据式 (13)和(14)求出各有利属性和不利属性指标名义值的加权值S+和S-。本文MCF、SEA、CLE为有利属性，PCF为不利属性。接着根据式(17)和(18)，计算出相对重要性值Qi和定量效用值Ui，Ui越大，管的综合耐撞性越好。最后，根据Ui对FSPTTs和FBPTTs的综合耐撞性进行排名，(如表3和表4所示)。由表3可知，在所有冲击角度下FSPC都排名第1。同样，由表4可知，在所有冲击角度下FBPC都排名第1。因此综合考虑多种冲击角度时，FSPC较其他FSPTTs具有更稳定的耐撞性；FBPC较其他FBPTTs具有更稳定的耐撞性。

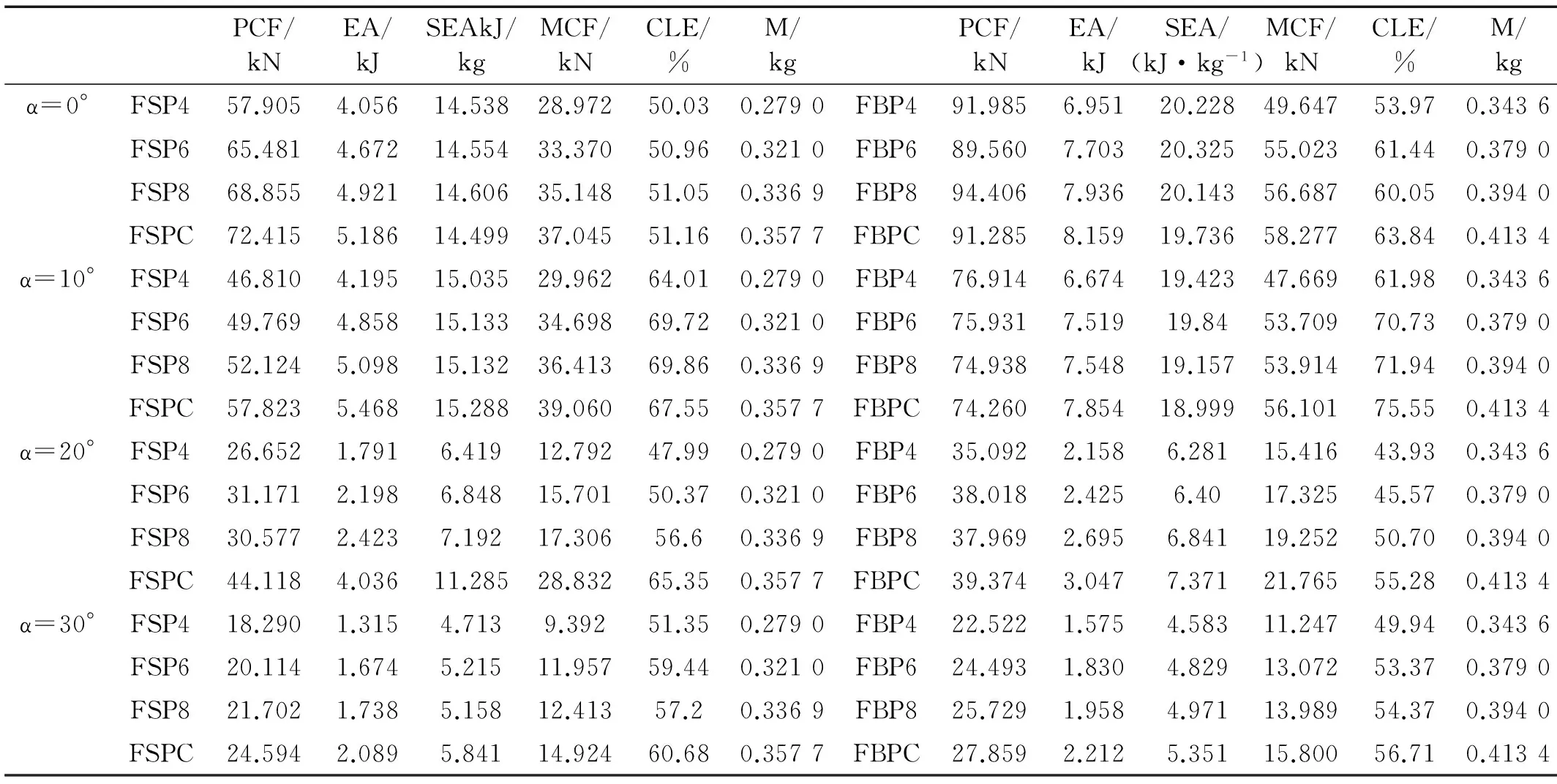
表2　FSPTTs与FBPTTs各性能指标评估值Tab.2 Performance criteria of FSPTTs and FBPTTs

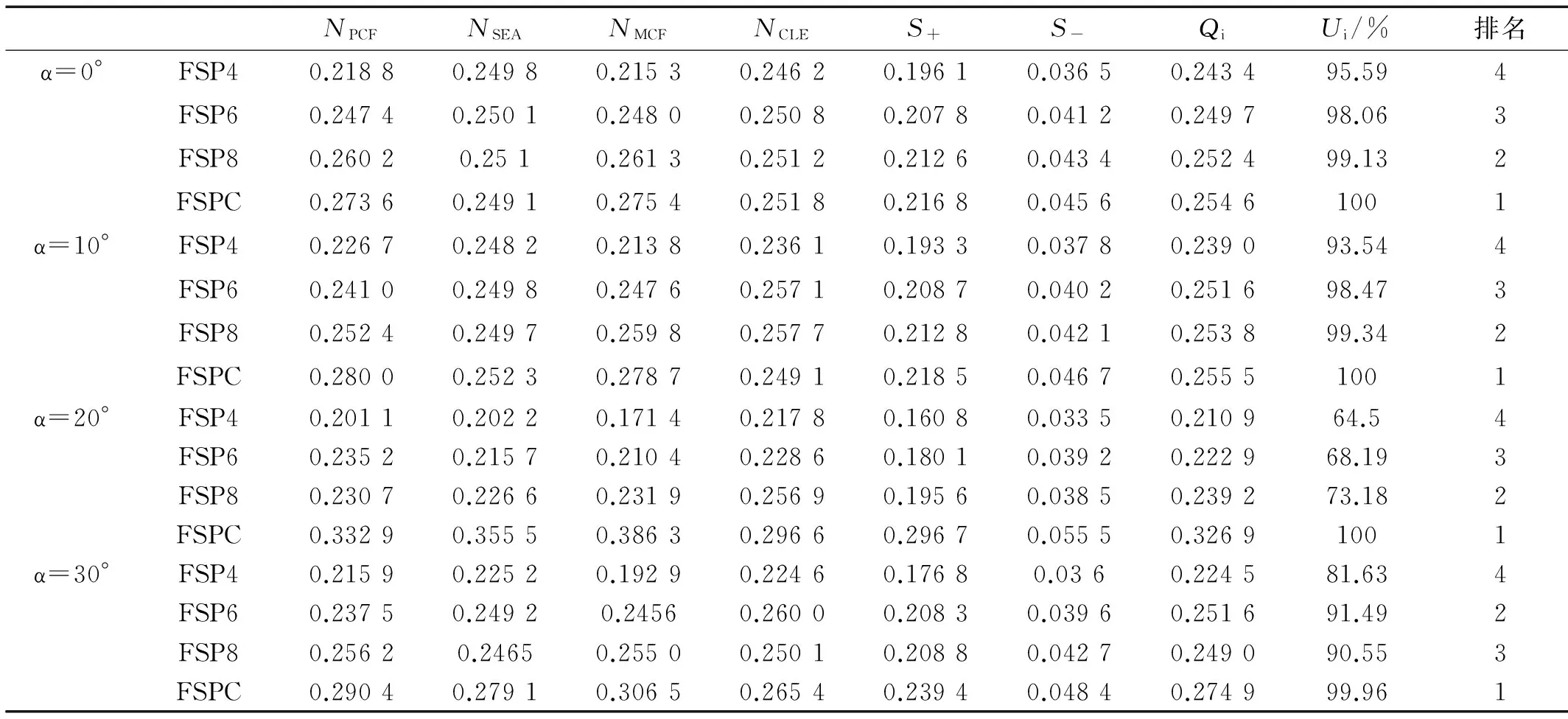
表3　 FSPTTs在COPARS评估方法中各性能值Tab.3 Performance value in COPARS for FSPTTs

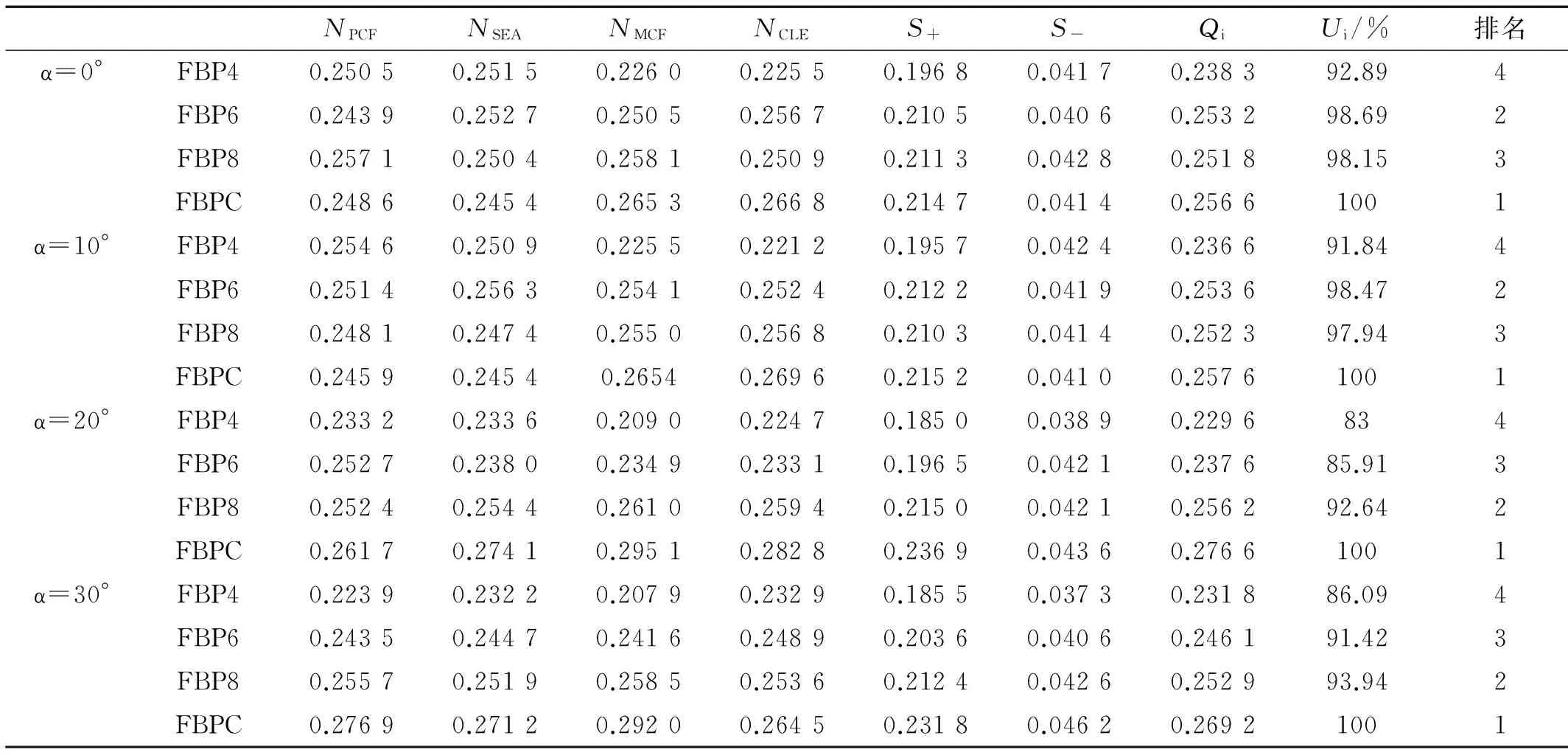
表4 FBPTTs在COPARS评估方法中各性能值Tab.4. Performance value in COPARS for FBPTTs

2.3加载角度对FSPC与FBPC耐撞性影响

前文分析表明FSPC和FBPC分别较其它FSPTTs和其他FBPTTs具有更好的耐撞性，本节进一步研究FSPC和FBPC在斜向加载下的变形机理。加载角度对FSPC和FBPC比吸能(SEA)的影响如图6所示，图中可以看出两种结构比吸能都随加载角度的增加呈下降趋势，而且比吸能与加载角度的关系都可以分为三个区域：①逐级变形区域; ②渡变形区域; ③整体折弯区域。FSPC与FBPC在过渡区域的临界角分别为：17°-21°和16°-17°。通过过渡区域FSPC比吸能下降了41.1%，FBPC比吸能下降了44.8%。可以看出FSPC过渡区域范围要宽于FBPC，因此比吸能通过过渡区域的变化量较FBP要平缓。此外，由图6可知，在加载角度小于FBPC进入过渡区域时的临界角(16°)时，FBPC的比吸能要高于FSPC，而在加载角度大于FBPC进入过渡区域时的临界角(16°)时，则FSPC的比吸能要高于FBPC。

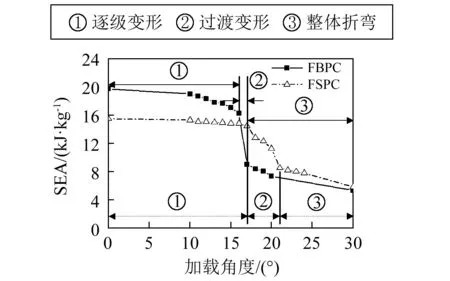
图6　加载角度对FSPC和FBPC比吸能的影响Fig.6 Effect of load angle on the SEA of FSPC and FBPC

3　多目标优化

前文分析表明FSPC和FBPC分别较其它FSPTTs和其他FBPTTs具有更好的耐撞性，因此本节将选择FSPC与FBPC进行优化设计。作为一种吸能结构，要求单位质量吸收的能量越多越好，比吸能SEA最大化应作为结构耐撞性优化问题的一个目标函数。另一方面，冲击峰值力是缓冲物体安全性的一个重要指标，应该控制在一定的水平范围内，故将峰值力PCF最小化作为结构耐撞性优化问题的另一个目标函数。因此，FSPC与FBPC在特定冲击角度αi下的优化问题可以表示为

(21)

式中：ρ为泡沫密度；t为壁厚；θ为外管顶部与底部横截面内径之比，上下界对应锥角分别为2.86°和8.53°。FBPC在优化过程中外管和内管保持相同壁厚，内管顶部与底部横截面内径的比值与外管相同。

为了准确地表述目标函数SEA和PCF，运用优拉丁试验设计方法，对FSPC和FBPC在每个特定冲击角度下分别设计了21组试验，通过有限元仿真获得目标响应，构建代理模型。通常运用的代理模型有响应面模型、移动最小二乘法、克里金模型(Kriging)和前馈神经网络等[32]，其中Kriging模型对高度非线性耐撞性优化问题具有良好的近似精度，本文将采用Kriging模型作为代理模型。代理模型的精度直接影响着Pareto前沿的精度，优化前必须对Kriging模型的精度进行验证。传统预测精度验证指标如R2和调整后R2不适用于Kriging模型，在此分别从每个典型冲击角度下设计域中随机抽取4个样本点，用相对误差来评价代理模型的精度。相对误差Re定义为

(22)

式中：f1(x)和f2(x)分别为随机样本点的仿真值和Kriging模型预测值。FSPC与FBPC在每组冲击角度下随机样本点的仿真值与预测值的相对误差分别如表5、表6所示。从表5和表6中可以看出，设计目标(SEA和PCF)的Kriging模型样本点相对误差都小于4%，说明代理模型的精度满足要求，可以用于后续优化研究。

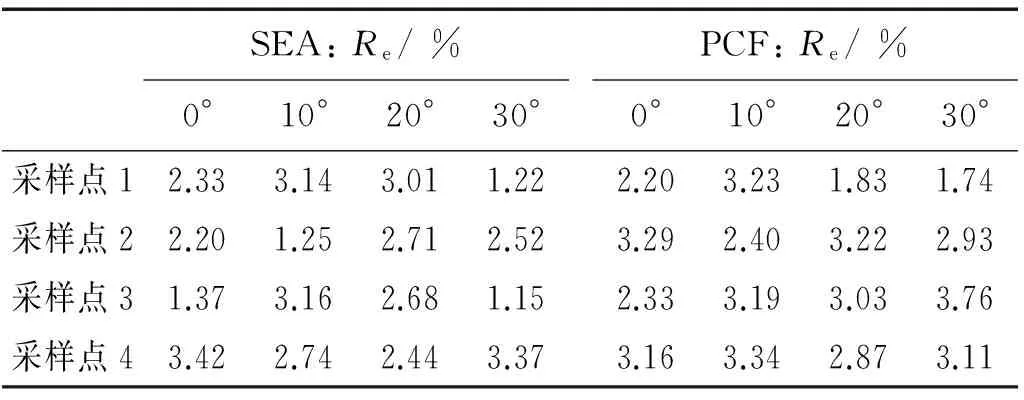
表5　FSPC相对误差Tab.5 Relative errors of design objectives of FSPC

表6　FBPC相对误差Tab.6 Relative errors of design objectives of FBPC

优化设计的目的就是寻求优化问题的Pareto解集，目前非支配遗传算法(NAGA-Ⅱ)、多目标粒子群算法(MOPSO)[33]和多目标模拟退火方法(MOSA)[34]被证明是有效的优化算法并被广泛应用于结构耐撞性优化设计中。本文采用非支配遗传算法(NAGA-Ⅱ)对FSPC与FBPC进行多目标优化。实际上，Patero前沿就是一系列优化方案的需求点，工程师可以根据实际需求在所得 Pareto前沿中得到他们想要的优化点。

通过NAGA-Ⅱ算法获得的FSPC与FBPC的Pareto前沿曲线如图7所示。图中可以看出FSPC和FBPC在每种冲击角度下，SEAαi和-PCFαi都呈负相关，即随着-PCFαi的增大使得SEA逐渐减小。由图7(a)可知，当冲击角度从0°变化到10°时，FSPC的Pareto前沿曲线变化不大；当冲击角度从10°变化到30°时，冲击角度对Pareto前沿曲线的位置和形状影响较为明显：FSPC的Pareto前沿曲线向右下方移动，而且Pareto解集范围逐渐变小，此外，Pareto前沿曲线在加载角度为30°时显著低于加载角度为0°、10°和20°时，原因是优化后的FSPC在加载角度为0°、10°和20°时呈现一定程度上的逐级变形模式，而在加载角度为30°时呈现完全整体折弯变形模式。由图7(b)可知，同FSPC相似，当冲击角度从0°变化到10°时，FBPC的Pareto前沿曲线变化不大；当冲击角度从10°变化到30°，FBPC的Pareto前沿曲线向右下方移动，而且Pareto前沿曲线在加载角度为20°和30°时显著低于加载角度为0°和10°时，原因是优化后的FBPC在加载角度为0°和10°时呈现一定程度上的逐级变形模式，而在加载角度为20°和30°时呈现完全整体折弯变形模式。此外，当冲击角度从10°变化到20°时，FBPC的Pareto前沿曲线的下移幅度显著大于FSPC的Pareto前沿曲线的下移幅度。原因是优化后在冲击角度为20°时，FBPC呈现完全整体折弯变形模式，而FSPC呈现一定程度上的逐级变形 (如图8所示)。

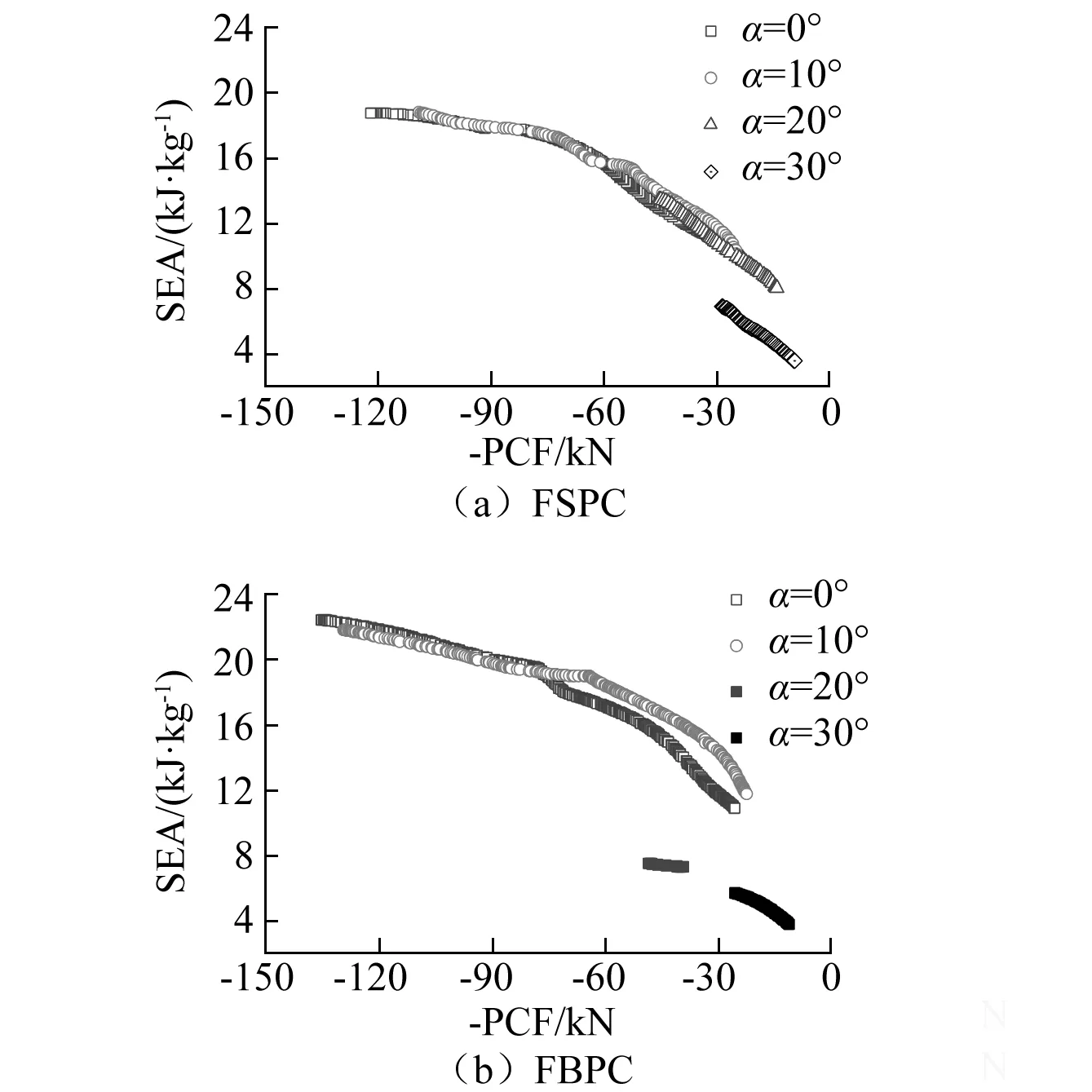
图7　不同加载角度下结构Pareto曲线Fig.7 Pareto fronts for FSPC and FBPC under different loading angles.

图8 加载角度为20°时结构变形模式

FSPC与FBPC在相同冲击角度下的Pareto前沿曲线如图9所示，由图9(a)和(b)可知，在冲击角度为0°和10°时，FBPC的Pareto前沿曲线要高于FSPC的Pareto前沿曲线，即在相同峰值力下，FBPC的SEA要高于FSPC的SEA。而在冲击角度为20°和30°时，FSPC的Pareto前沿曲线要高于FBPC的Pareto前沿曲线，上文分析了其原因，即优化后FBPC呈现完全整体折弯变形模式，而FSPC呈现一定程度上的逐级变形(如图8所示)。因此，在冲击角度为0°和10°时，FBPC的耐撞性优于FSPC，而在冲击角度为20°和30°时，FSPC的耐撞性优于FBPC。

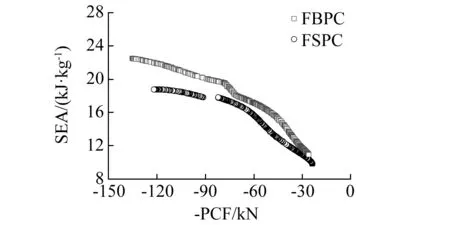
(a) α=0°

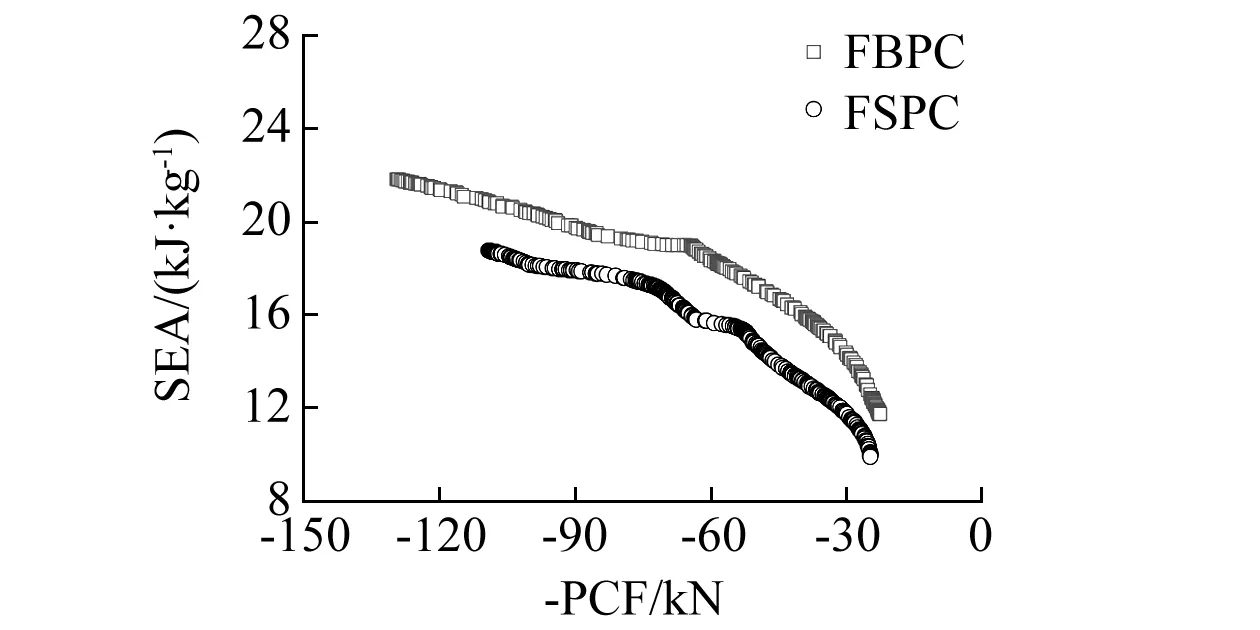
(b) α=10°

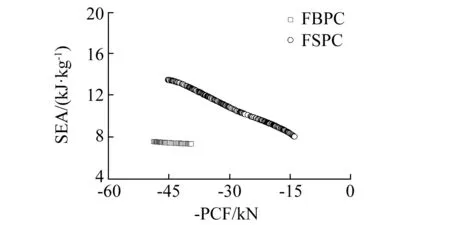
(c) α=20°

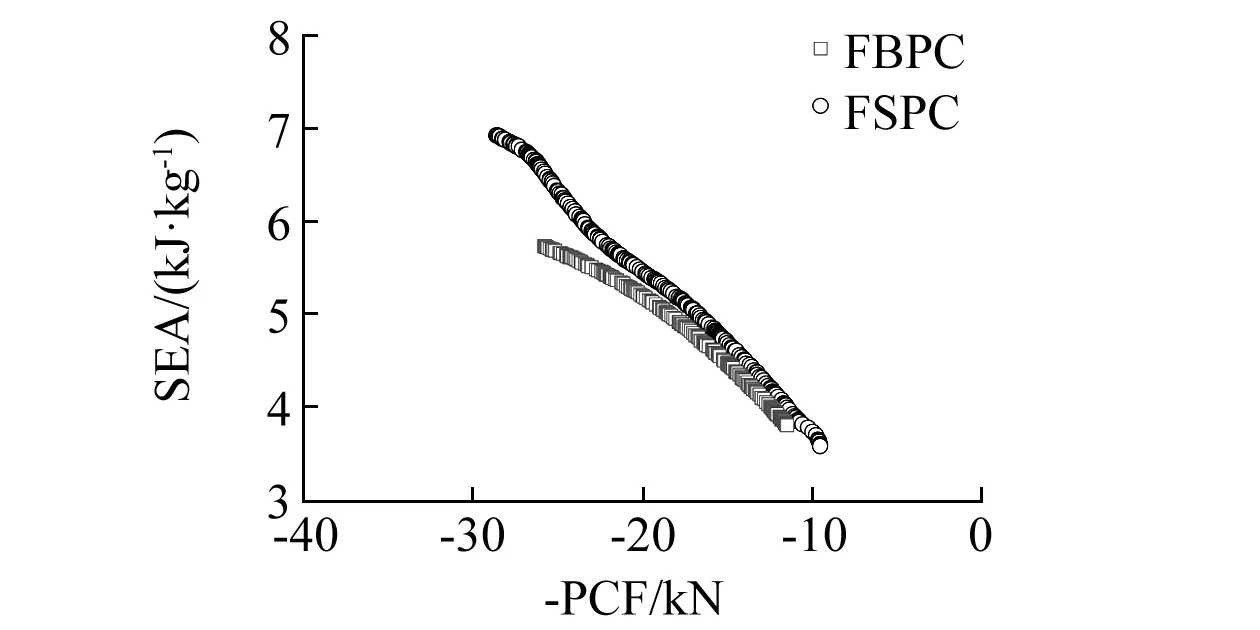
(d) α=30°

4　结　论

本文采用非线性有限元方法，对四种不同横截面的泡沫填充单锥管与泡沫填充双锥管在四种冲击角度下的耐撞性进行了仿真分析。在所有冲击角度下，泡沫填充单锥管与泡沫填充双锥管的吸能量与平均压缩力均随着横截面边数的增加而增加。采用COPRAS评估方法综合考虑四种耐撞性指标，分别对不同横截面的泡沫填充单锥管与泡沫填充双锥管的耐撞性进行了评估。结果表明，综合考虑多种冲击角度时，圆形截面泡沫填充单锥管较其他截面泡沫填充单锥管具有更好的耐撞性；圆形截面泡沫填充双锥管较其他截面泡沫填充双锥管具有更好的耐撞性。

采用非支配遗传算法对圆形截面泡沫填充单锥管和圆形截面泡沫填充双锥管在四种冲击角度下进行了多目标优化，结果表明当冲击角度从0°变化到10°时，圆形截面泡沫填充单锥管与圆形截面泡沫填充双锥管的Pareto曲线变化不大，而当冲击角度从10°变化到30°时，冲击角度对Pareto曲线形状和位置有显著影响。在冲击角度为0°和10°时圆形截面泡沫填充双锥管的耐撞性优于圆形截面泡沫填充单锥管，而在冲击角度为20°和30°时圆形截面泡沫填充单锥管的耐撞性优于圆形截面泡沫填充双锥管。在实际应用中，可以根据工程需要选择合适的结构。

[ 1 ] AHMAD Z, THAMBIRATNAM D P. Application of foam-filled conical tubes in enhancing the crashworthiness performance of vehicle protective structures [J]. International Journal of Crashworthiness, 2009, 14(4): 349-363.

[ 2 ] 文桂林, 孔祥正, 尹汉锋, 等. 泡沫填充夹芯墙多胞结构的耐撞性多目标优化设计 [J]. 振动与冲击, 2015, 34(5): 115-121. WEN Guilin,KONG Xiangzheng,YIN Hanfeng, et al. Multi-objective crashworthiness optimization design of foam-filled sandwich wall multi-cell structures[J]. Journal of Vibration and Shock, 2015, 34(5): 115-121.

[ 3 ] HAN D C, PARK S H. Collapse behavior of square thin-walled columns subjected to oblique loads [J]. Thin-Walled Structures, 1999, 35(3): 167-184.

[ 4 ] REYES A, LANGSETH M, HOPPERSTAD O S. Square aluminum tubes subjected to oblique loading [J]. International Journal of Impact Engineering, 2003, 28(10): 1077-1106.

[ 5 ] REYES A, LANGSETH M, HOPPERSTAD O S. Crashworthiness of aluminum extrusions subjected to oblique loading: experiments and numerical analyses [J]. International Journal of Mechanical Sciences, 2002, 44(9): 1965-1984.

[ 6 ] REYES A, HOPPERSTAD O S, LANGSETH M. Aluminum foam-filled extrusions subjected to oblique loading: experimental and numerical study [J]. International Journal of Solids and Structures, 2004, 41(5/6): 1645-1675.

[ 7 ] MAMALIS A, MANOLAKOS D, IOANNIDIS M, et al. Numerical simulation of thin-walled metallic circular frusta subjected to axial loading [J]. International Journal of Crashworthiness, 2005, 10(5): 505-513.

[ 8 ] GUPTA N, PRASAD G E, GUPTA S. Plastic collapse of metallic conical frusta of large semi-apical angles [J]. International Journal of Crashworthiness, 1997, 2(4): 349-366.

[ 9 ] NAGEL G, THAMBIRATNAM D. Dynamic simulation and energy absorption of tapered tubes under impact loading [J]. International Journal of Crashworthiness, 2004, 9(4): 389-399.

[10] REID S, REDDY T. Static and dynamic crushing of tapered sheet metal tubes of rectangular cross-section [J]. International Journal of Mechanical Sciences, 1986, 28(9): 623-637.

[11] AHMAD Z, THAMBIRATNAM D P. Dynamic computer simulation and energy absorption of foam-filled conical tubes under axial impact loading [J]. Computers & Structures, 2009, 87(3/4): 186-197.

[12] AHMAD Z, THAMBIRATNAM D P, TAN A C C. Dynamic energy absorption characteristics of foam-filled conical tubes under oblique impact loading [J]. International Journal of Impact Engineering, 2010, 37(5): 475-488.

[13] ZHANG Y, SUN G, XU X, et al. Multiobjective crashworthiness optimization of hollow and conical tubes for multiple load cases [J]. Thin-Walled Structures, 2014, 82(3):331-342.

[14] HOU S, HAN X, SUN G, et al. Multiobjective optimization for tapered circular tubes [J]. Thin-Walled Structures, 2011, 49(7): 855-863.

[15] ZHANG Y, SUN G, LI G, et al. Optimization of foam-filled bitubal structures for crashworthiness criteria [J]. Materials & Design, 2012, 38(1):99-109.

[16] ZHENG G, WU S, SUN G, et al. Crushing analysis of foam-filled single and bitubal polygonal thin-walled tubes [J]. International Journal of Mechanical Sciences, 2014, 87(1):226-240.

[17] LU G, YU T. Energy absorption of structures and materials [M]. Amsterdam: Elsevier, 2003.

[18] CAO L, ZHOU Z, JIANG B, et al. Development and validation of the FE model for a 10-year-old child head [J]. Chinese Journal of Biomedical Engineering, 2014, 31(1): 63-70.

[19] KIM H S. New extruded multi-cell aluminum profile for maximum crash energy absorption and weight efficiency [J]. Thin-Walled Structures, 2002, 40(4): 311-327.

[20] SANTOSA S P, WIERZBICKI T, HANSSEN A G, et al. Experimental and numerical studies of foam-filled sections [J]. International Journal of Impact Engineering, 2000, 24(5): 509-534.

[21] LANGSETH M, HOPPERSTAD O. Static and dynamic axial crushing of square thin-walled aluminium extrusions [J]. International Journal of Impact Engineering, 1996, 18(7): 949-968.

[22] DESHPANDE V, FLECK N. Isotropic constitutive models for metallic foams [J]. Journal of the Mechanics and Physics of Solids, 2000, 48(6): 1253-1283.

[23] ZHANG Z, LIU S, TANG Z. Comparisons of honeycomb sandwich and foam-filled cylindrical columns under axial crushing loads [J]. Thin-Walled Structures, 2011, 49(9): 1071-1079.

[24] HANSSEN A, HOPPERSTAD O, LANGSETH M, et al. Validation of constitutive models applicable to aluminium foams [J]. International Journal of Mechanical Sciences, 2002, 44(2): 359-406.

[25] REYES A, HOPPERSTAD O, BERSTAD T, et al. Constitutive modeling of aluminum foam including fracture and statistical variation of density [J]. European Journal of Mechanics-A/Solids, 2003, 22(6): 815-835.

[26] CHATTERJEE P, ATHAWALE V M, CHAKRABORTY S. Materials selection using complex proportional assessment and evaluation of mixed data methods [J]. Materials & Design, 2011, 32(2): 851-860.

[27] HANSSEN A G, LANGSETH M, HOPPERSTAD O S. Static and dynamic crushing of square aluminium extrusions with aluminium foam filler [J]. International Journal of Impact Engineering, 2000, 24(4): 347-383.

[28] MIRFENDERESKI L, SALIMI M, ZIAEI-RAD S. Parametric study and numerical analysis of empty and foam-filled thin-walled tubes under static and dynamic loadings [J]. International Journal of Mechanical Sciences, 2008, 50(6): 1042-1057.

[29] YIN H, WEN G, FANG H, et al. Multiobjective crashworthiness optimization design of functionally graded foam-filled tapered tube based on dynamic ensemble metamodel [J]. Materials & Design, 2014, 55(1):747-757.

[30] ABRAMOWICZ W, JONES N. Dynamic progressive buckling of circular and square tubes [J]. International Journal of Impact Engineering, 1986, 4(4): 243-270.

[31] TARLOCHAN F, SAMER F, HAMOUDA A, et al. Design of thin wall structures for energy absorption applications: Enhancement of crashworthiness due to axial and oblique impact forces [J]. Thin-Walled Structures, 2013, 71(1):7-17.

[32] SONG X, SUN G, LI G, et al. Crashworthiness optimization of foam-filled tapered thin-walled structure using multiple surrogate models [J]. Structural and Multidisciplinary Optimization, 2012, 47(2): 221-231.

[33] SUN G, LI G, STONE M, et al. A two-stage multi-fidelity optimization procedure for honeycomb-type cellular materials [J]. Computational Materials Science, 2010, 49(3): 500-511.

[34] QI C, YANG S, DONG F. Crushing analysis and multiobjective crashworthiness optimization of tapered square tubes under oblique impact loading [J]. Thin-Walled Structures, 2012, 59(1):103-119.

Crashworthiness analysis of foam-filled single and bitubal polygonaltapered thin-walled tubes under oblique impact loading

CHEN Yafeng, BAI Zhonghao

(The State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Changsha 410082, China)

The foam-filled taper tube, which combines the advantages of foam-filled structures and taper structures, has excellent abilities of energy absorption and buckling deformation resisting. The crashworthiness of foam-filled single polygonal tapered tubes(FSPTTs) and foam-filled bitubal polygonal tapered tubes(FBPTTs) under oblique impact loading was studied. A complex proportional assessment and evaluation method(COPRAS) was adopted to evaluate the comprehensive crashworthiness of FSPTTs and FBPTTs. It is found that the foam-filled single circular (FSC) tube and foam-filled bitubal circular (FBC) tube respectively perform better than FSPTTs and FBPTTs with other cross sectional configurations. The multiobjective optimization was conducted on the FSC and FBC tubes under four different impact angles to maximize the specific energy absorption and peak force. The results show that the Pareto curves of both FSC and FBC tubes have only little change when the impact angle changes from 0° to 10°，while the impact angle has significant effect on the Pareto curves when the impact angle changes from 10° to 30° . The FBC tube performs better when the impact angle is 0° or 10°，while the FSC tube performs better when the impact angle is 10° or 20° . Appropriate structures can be chosen to meet practical application requirements.

foam filled; tube; crashworthiness; tapered tube; oblique impact; multiobjective optimization

国家自然科学基金(面上项目)(51475153)

2015-10-22修改稿收到日期： 2016-01-24

陈亚枫 男，硕士，1991年7月生

白中浩 男，博士，副教授，1978年10月生

TH212；TH213.3

A

10.13465/j.cnki.jvs.2017.06.004