WSN中最小延时的数据汇集树构建与传输调度算法
李浩光, 胡玉鹏
(1. 广东工程职业技术学院 信息工程学院, 广州 510520; 2. 湖南大学 软件学院, 长沙 410082)
WSN中最小延时的数据汇集树构建与传输调度算法
李浩光1, 胡玉鹏2
(1. 广东工程职业技术学院 信息工程学院, 广州 510520; 2. 湖南大学 软件学院, 长沙 410082)

针对现有无线传感器网络数据汇集算法延时较大这一不足,对最小延时数据汇集树和传输调度问题进行了研究。提出一种基于度约束的汇集树构建算法(DCAT)。该算法按照BFS方式遍历图,当遍历到每个节点时,通过确定哪些节点与汇点更近来确定潜在母节点集合。然后,选择图中度数最小的潜在母节点作为当前被遍历节点的母节点。此外,为了在给定的汇集树上进行高效数据汇集,文中还提出两种新的基于贪婪的TDMA传输调度算法:WIRES-G和DCAT-Greedy。利用随机生成的不同规模的传感器网络,参照当前最新算法,对本方法的性能进行了全面评估。结果表明,与当前最优算法相比,本调度算法与汇集树构建算法结合起来,可显著降低数据汇集的延时。
无线传感器网络; 数据汇集; 最小延时; 度约束; 传输调度
0 引 言
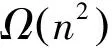
此外,文献[9]中提出了称为均衡式最短路径树(BSPT)的构建算法和称为基于加权增量排序的汇集调度(WIRES)算法来实现数据汇集。BSPT算法给出了数据汇集延时的范围为max{xi+hi:i=1,2,k,n}的下界,其中xi和hi分别为指定树中节点i从根节点开始的子节点数量和跳数。它采取宽度优先搜索方式遍历图,然后采用双枝半匹配算法[10]来构建可使延时最小的最短路径树。而WIRES调度算法则将汇集树作为输入,并将树中所有叶节点作为可在单位时间内被调度的合格节点。为每个合格节点计算一个权重,权重越高,表明该节点在当前时隙内被调度的优先级越高。然后挨个考察合格节点,对于在传输时不与先前节点发生干扰的所有节点进行调度。所有节点考虑完毕后,一个轮次完毕,通过删除已被调度的节点,增加从各个子节点接收到数据的母节点来更新合格节点集合。重复上述步骤,直到所有节点被调度一次。然而该方法使用汇集树中非叶相邻节点的数量来进行权重计算,因为节点被调度后从汇集树中删除,所以每一轮次均需重新计算权重,导致数据汇集延时增大,且额外耗费了能量。
针对以上方法的不足,提出一种新的汇集树构建算法,称为度约束汇集树(Degree-Constrained Aggregation Tree,DCAT)。此外,本文还提出两种新的调度算法,称为WIRES-G和DCAT-Greedy。通过全面的仿真实验评估了汇集树构建算法和调度算法的性能,并与当前最优算法BSPT-WIRES[9]进行了性能比较。结果表明,DCAT算法与WIRES调度算法结合起来可将延时性能提升21%。如果将调度算法WIRES-G与DCAT算法结合起来,可实现进一步的性能提升,将这种融合算法称为DCAT-WIRES-G。此外,DCAT-Greedy的性能比BSPR-WIRES高出32%~40%,具体取决于网络规模大小。
1 网络模型和问题描述
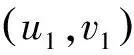
假设节点同步,且共享相同的无线信道。假设所有节点固定布置,传输范围相同且恒定。同时假设干扰半径等于传输半径[12]。时间经过时隙处理,每个节点经过调度后在指定时隙内传输数据。如果在同一时隙内传输数据时不会发生干扰,则两个节点可在同一时隙内传输数据。还假设节点具有求取最小值、最大值、求和和计数功能,将n个数据元素作为输入,产生一个元素作为输出。
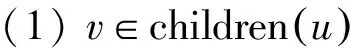
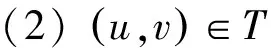
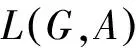
2 基于度约束的汇集树(DCAT)
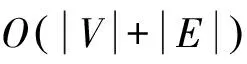
在图1中,实线表示汇集树的边,虚线表示图中未作为树边的边。图1(a)是BSPT算法构建的汇集树,可以看出,该树的最优调度需要4个时隙。图1(b)是DCAT算法针对同一图形构建的汇集树,此时,最优调度只需要3个时隙。图1表明为何DCAT中采用的方法可获得优于BSPT的性能。该图中,子节点被均匀分布于潜在母节点之间,且与它们在图中的度无关,于是调度算法受到的约束更多。由图可以清晰看出,考虑图中节点的度数,其性能要优于使汇集树的度最小化。这表明,DCAT更适合构建高效的汇集树,至少当不同节点具有不同度数时如此。
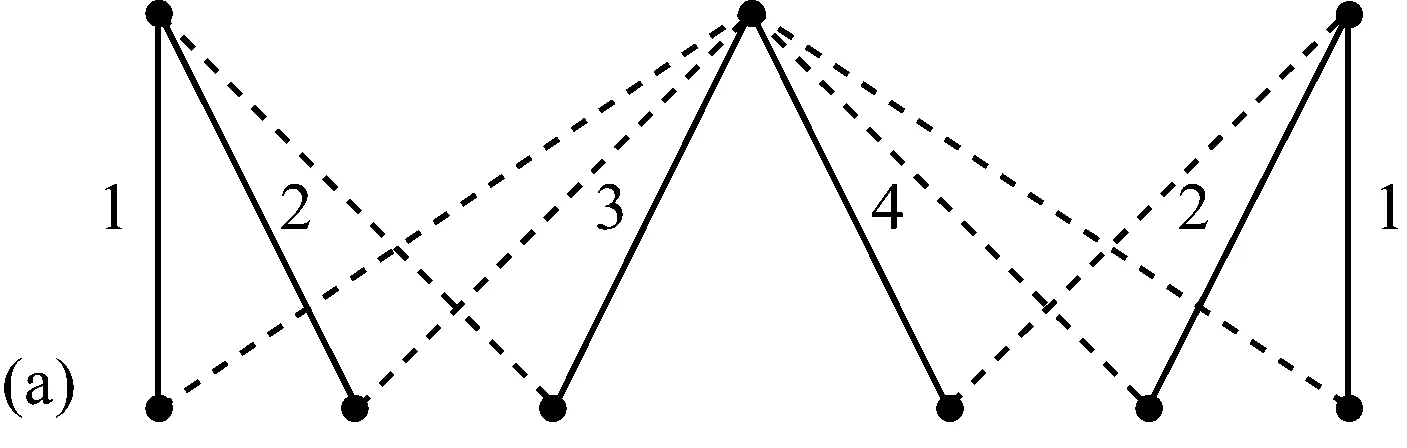
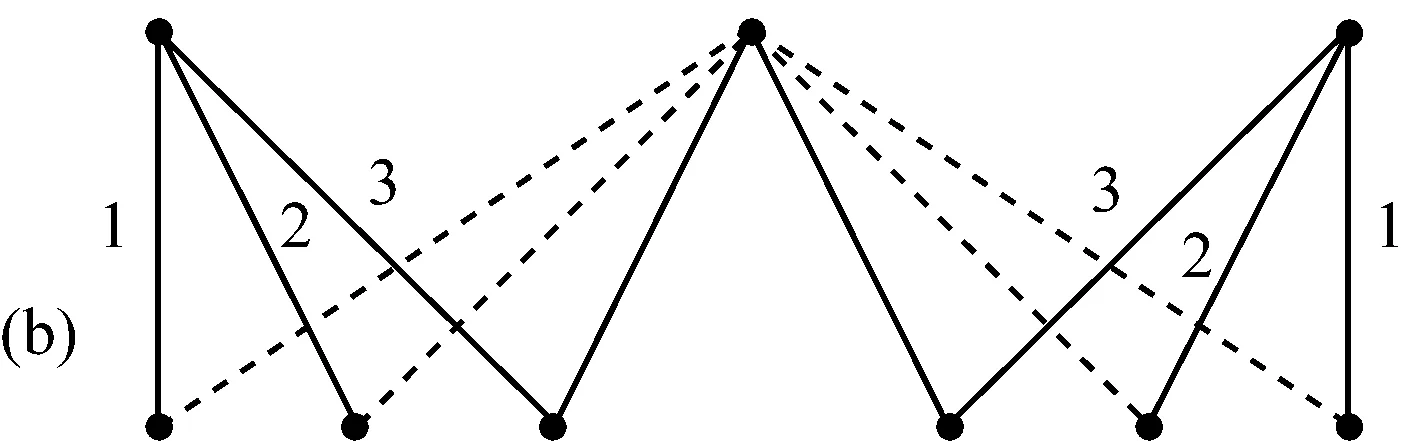
图1 DCAT算法和BSPT算法构建的汇集树比较

算法1 DCAT输入:G=V,E(),s:汇点输出:图G以s为根的生成树,其中v.p表示v∈V的母节点1.procedureDCATG,s()2.foreachu∈G.Vdo3.u.d=-14.u.p=nil5.endfor6.s.d=07.Q=Ø8.Enqueue(Q,s)9.whileQ≠Ødo
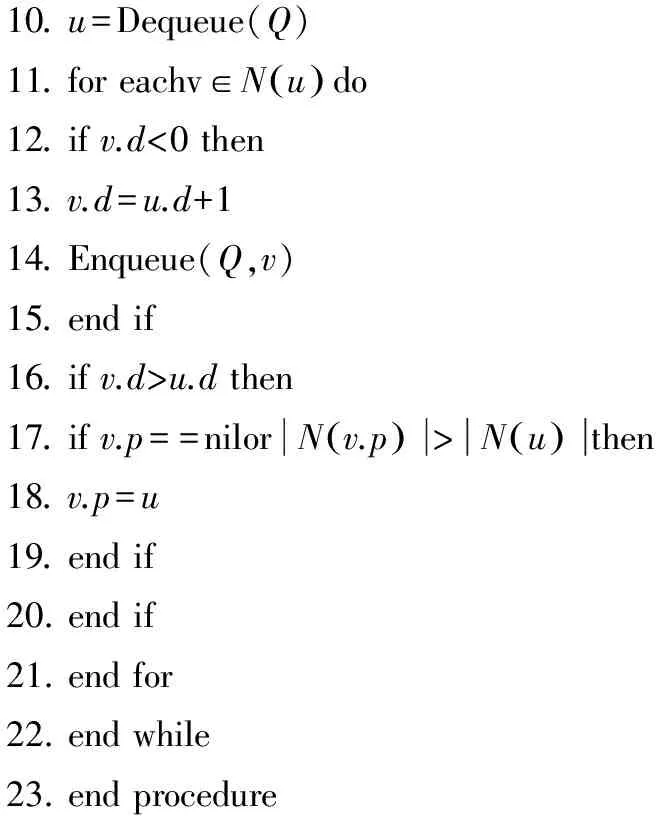
10.u=Dequeue(Q)11.foreachv∈Nu()do12.ifv.d<0then13.v.d=u.d+114.Enqueue(Q,v)15.endif16.ifv.d>u.dthen17.ifv.p==nilorNv.p()>Nu()then18.v.p=u19.endif20.endif21.endfor22.endwhile23.endprocedure
3 调度算法
本节给出了两种用于数据汇集的调度算法。第1种算法称为WIRES-G,是对文献[9]中WIRES算法的一种改进:在WIRES算法中增加一个步骤,以便每个时隙期间调度更多个节点。每一轮次中,新添步骤需要为原来算法无法调度的合格节点匹配新的母节点。WIRES-G的具体内容请见算法2(G表示贪婪)。工作流程如下。第5~9行表示原来WIRES算法每一轮次的步骤。第9行结束时,S包含经过调度将在时间j发送数据的节点,R包含从S中节点接收数据的节点集合。此时,如果继续保持原来的树,则其他所有节点经过调度后传输数据总会与已被调度的节点发生干扰。

算法2 WIRES⁃G输入:G=V,E(),s:汇点,v.p:树中v∈V的母节点输出:G的一个有效调度,其中v.t表示v∈V的传输时间1.procedureWIRES⁃G(G;s)2.∀v∈G.Vv.t=0//对时隙初始化3.j=14.whiles.t=0do5.L=GETELIGIBLENODES(G)6.COMPUTEWEIGHTS(L)7.SORTDECREASING(L)8.S=R=Ø//发送节点和接收节点集合开始时为空9.SCHEDULENODES(L;S;R)10.L=LS//将发送节点从合格节点中删除11.GREEDY⁃SCHEDULING(L;S;R)12.j=j+113.endwhile14.endprocedure15.procedureSCHEDULENODES(L;S;R)16.foreachu∈Ldo17.ifu∉NR()且u.p∉NS()then//如果u在传输时不发生冲突18.u.t=j//通过调度使u在时间j传输

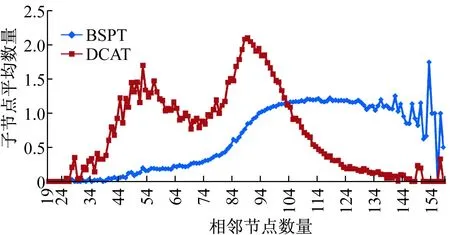
19.S=S∪u{}20.R=R∪u.p{}21.endif22.endfor23.endprocedure24.procedureGREEDY⁃SCHEDULING(L;S;R)25.foreachu∈Ldo26.ifu∉R且u∉NR()then27.r=nil//未发现母节点28.foreachp∈Nu()do//寻找母节点29.ifp.t==0且p∉NS()且(r=nil或Np() 在算法2的GREEDY-SCHEDULING中,对之前未被顺利调度的所有合格节点进行迭代。首先,考查当前节点p是否已经不再作为接收节点,同时考察该节点在传输数据时是否会对R中的接收节点造成干扰。如果如此,则为p选择一个未被调度且可在时间j传输数据并不发生干扰的相邻节点,同时该相邻节点的度在图中所有类似相邻节点间最小。找到相邻节点后,便将其作为当前节点在汇集树中新的母节点。如果先前母节点未遗留下未被调度的子节点,并且在当前轮次内不作为接收节点,则将其添加到合格节点列表中,原因是它可在时间j被调度(第36~38行)。 本文提出的第2种调度算法称为DCAT-Greedy,具体内容见算法3。该算法融合了本文的汇集树构建算法DCAT及GREEDY-SCHEDULING算法,目的是进一步降低延时。DCAT-Greedy算法首先采用DCAT构建一个汇集树。每次迭代时,确定哪些节点有资格在此轮接受调度。只有所有子节点均被分配了一个时隙的节点才是有资格被调度的节点(合格节点)。DCAT-Greedy采用与WIRES相同的方法计算权重(非叶相邻节点的数量),并根据权重对节点降序排列。然后,GREEDY-SCHEDULING对所有合格节点进行迭代,在不发生干扰的前提下使尽可能多的节点被调度。 算法3 DCAT⁃Greedy输入:G=V,E(),s:汇点输出:G以s为根的生成树,及G的一个有效调度,其中v.t和v.p分别表示v∈V的传输时间和母节点1.procedureDCAT⁃GREEDY(G)2.DCAT(G;s)3.∀v∈G.Vv.t=0//时隙初始化4.j=15.whiles.t=0do6.L=GETELIGIBLENODES(G)7.COMPUTEWEIGHTS(L)8.SORTDECREASING(L)9.S=R=Ø10.GREEDY⁃SCHEDULING(L;S;R)11.j=j+112.endwhile13.endprocedure 结合小型、中型和大型无线传感器网络对汇集树构建算法DCAT及传输调度算法进行性能评估,通过将节点随机均匀分布于5×5、10×10和20×20的地理区域上生成小型、中型和大型网络。节点的传输范围为1,节点的密度范围为8~200,其中密度定义为图中节点的平均度。如果节点间的欧氏距离小于等于传输范围,则认为节点连通。对每个被选密度值,共生成100个连通图,对这100个图求取平均作为最终结果。 首先单独评估汇集树构建算法。比较DCAT-WIRES和BSPT-WIRES的性能,同时衡量了所生成调度方案的延时。如图2所示,网络尺寸20×20,采用WIRES调度。DCAT树无论在哪种密度设置下,延时均较低。鉴于篇幅有限,这里只给出大型网络的运行结果,对小型和中型网络具有相同结论。 图2 DCAT和BSPT树的平均汇集延时性能比较 图3在一定程度上表明了DCAT算法性能优于复杂性更高的BSPT算法的原因。该图给出了图中相邻节点数量与汇集树上子节点平均数量之间的关系。可以看出,与DCAT相比,BSPT分配给度数更高节点(高度节点)的子节点更多,而DCAT倾向于为度数低于网络密度的节点分配较多子节点。如果以度数较高的节点作为母节点,则调度算法可在同一时隙内调度更多个节点,有助于降低调度的总体延时。 图3 图的度数与汇集树子节点平均数量之间的关系 下面评估WIRES-G和DCAT-Greedy两种调度算法的性能。图4给出了WIRES-G、DCAT-Greedy和WIRES在小型传感器网络上的性能比较。很显然,DCAT-Greedy对小型网络的性能最优。可以看出,DCAT-Greedy所生成的调度方案的平均延时,要远低于其他算法,当密度设置较高时更是如此。DCAT-Greedy甚至远低于BSPT生成的汇集树的下界。当密度为200时,DCAT-Greedy的性能比排名第2的算法DCAT-WIRES-G高出25%,比先前最优算法BSPTWIRES高出近40%。此外,用百分比表示的性能增益随着密度稳定上升。鉴于篇幅所限,对中型网络的运行结果类似,此处略。可以看出,无论在哪种情况下,WIRES-G均可降低调度方案的延时,且与采用的树构建算法无关;WIRES无法实现这一性能。BSPTWIRES-G和DCAT-WIRES的性能比较接近,前者略优于后者。因此,无论是采用新提出的调度算法WIRES-G,还是新提出的树构建算法DCAT-Greedy,均可实现性能提升。DCAT-WIRES-G的性能优于其他算法,但低于DCAT-Greedy,且密度越大,性能增益越大。 图5给出了调度算法对大型传感器网络的性能。 图4 网络规模为5×5时平均汇集延时 结果特点与上文类似。然而,几乎在所有密度设置下,DCAT-WIRES的性能均优于BSPT-WIRES-G。实际上,对中等密度水平,DCATWIRES-G的性能比BSPT-WIRES-G高出15%。DCAT-Greedy和DCAT-WIRES-G的性能相近,但当密度在15~75(含)时,DCAT-WIRES-G略优于DCAT-Greedy。与BSPT-WIRES相比,DCAT-WIRES-G的性能提升了34.66 %,而DCAT-Greedy相对于BSPT-WIRES提升了32.25%。而DCAT-Greedy结果的标准差(4.48)低于DCAT-WIRES-G的标准差(5.35)。 图5 网络规模为20×20时平均汇集延时 为了更好理解性能特点,考察了图中节点度与汇集树中子节点平均数量之间的关系。图6给出了密度为30时中等随机网络下的关系。可以看出,各种基于DCAT的算法为度数较高的节点分配的子节点数量很少,这与笔者预期相一致。DCAT-Greedy算法为低度节点分配的子节点数量最多,为高度节点分配的子节点数量最少。这也是该算法在实验中表现优异的原因。对高密度设置具有类似特点。 另外,还考察了汇集树中子节点数量最多的节点所处位置。图7给出了中等规模网络在密度为30时的运行结果。可以看出,汇点(距离为0的节点)在除了DCAT-Greedy的各种算法下,子节点数量均较高。这是因为开始时采用最短路径树。因此,所有与汇点相距一跳距离的节点将是汇点的子节点。DCAT-Greedy不存在这个问题,因为它为了同时调度尽可能多的节点而修改了初始树。 图6 图的度数与汇集树子节点平均数量之间的关系 图7 汇集树中度数较高节点的位置(密度为30) 此外,发现如果使度较高的节点与树顶较近,往往会导致延时上升。这是因为与汇点的距离近了,可供选择的节点少了,并行化的概率便会降低。使度较高的节点位于树的底层,也不利于性能提升,因为只有当所有节点传输完毕才能使数据向上传输,这解释了为何对密度中等的大型网络,DCATWIRES-G的性能要优于DCAT-Greedy。为此,一种可能的思路是设计一种将上述两种算法综合起来的混合算法来提升面对大型传感器网络时的性能。例如,对树的底层采用DCAT-WIRES-G算法,对树的高层采用DCAT-Greedy算法。 本文研究了WSN中进行TDMA调度时的数据汇集问题,提出一种新的汇集树构建算法及两种新的调度算法。与当前最优算法相比,如果将本文提出的汇集树构建算法与调试算法结合起来,可显著降低延时。在下一步工作中,研究的重点主要包含两个方面:① 在多种应用场景下分析数据汇集可靠性与汇集树构建以及调度算法之间的关系,以进一步提高数据汇集的质量;② 基于压缩感知理论,分析数据汇集树的构建过程对于延长网络生命周期的影响,进而提出一种可提高网络生命周期的基于压缩感知的数据汇集算法。 [1] Bagaa M, Younis M, Djenouri D,etal. Distributed low-latency data aggregation scheduling in wireless sensor networks [J]. ACM Transactions on Sensor Networks (TOSN), 2015, 11(3): 49-60. [2] 石为人, 唐云建, 王燕霞. 基于拥塞控制的无线传感器网络数据汇集树生成算法[J]. 自动化学报, 2010, 36(6): 823-828. [3] Yousefi H, Malekimajd M, Ashouri M,etal. Fast aggregation scheduling in wireless sensor networks [J]. IEEE Transactions on Wireless Communications, 2015, 14(6): 3402-3414. [4] Liu X Y, Zhu Y, Kong L,etal. CDC: Compressive data collection for wireless sensor networks [J]. IEEE Transactions on Parallel and Distributed Systems, 2015, 26(8): 2188-2197. [5] 杨 庚, 李 森, 陈正宇, 等. 传感器网络中面向隐私保护的高精确度数据融合算法 [J]. 计算机学报, 2013, 36(1): 189-200. [6] 邱立达, 刘天键, 傅 平. 基于稀疏滤波的无线传感器网络数据融合[J]. 电子测量与仪器学报, 2015, 29(3): 352-357. [7] Guo L, Li Y, Cai Z. Minimum-latency aggregation scheduling in wireless sensor network [J]. Journal of Combinatorial Optimization, 2016, 31(1): 279-310. [8] Huang S C H, Wan P J, Vu C T,etal. Nearly constant approximation for data aggregation scheduling in wireless sensor networks[C]// 26th IEEE International Conference on Computer Communications(INFOCOM). Anchorage, Alaska, USA: IEEE Press, 2007: 366-372. [9] Malhotra B, Nikolaidis I, Nascimento M A. Aggregation convergecast scheduling in wireless sensor networks [J]. Wireless Networks, 2011, 17(2): 319-335. [10] Harvey N J A, Ladner R E, Lovász L,etal. Semi-matchings for bipartite graphs and load balancing[J]. Journal of Algorithms, 2006, 59(1): 53-78. [11] Incel Ö D, Ghosh A, Krishnamachari B,etal. Fast data collection in tree-based wireless sensor networks [J]. IEEE Transactions on Mobile Computing, 2012, 11(1): 86-99. [12] Yao Y, Cao Q, Vasilakos A V. EDAL: An energy-efficient, delay-aware, and lifetime-balancing data collection protocol for heterogeneous wireless sensor networks [J]. IEEE/ACM Transactions on Networking, 2015, 23(3): 810-823. Data Aggregation Tree Construction and Transmission Scheduling Algorithm Based on Minimum Latency in Wireless Sensor Networks LIHao-guang1,HUYu-peng2 (1. School of Information Engineering, Guangdong Engineering Polytechnic, Guangzhou 510520, China; 2. The Software College, Hunan University, Changsha 410082, China) Aiming at shortcomings of the large delay at the existing data aggregation algorithms in wireless sensor networks, we study the problem of the minimum latency data aggregation tree and transmission scheduling, and an aggregation tree construction algorithm based on degree constraint (DCAT) is proposed. It works by traversing the graph in a BFS manner. As it traverses each node, the set of potential parents is determined by identifying the nodes that are one-hop closer to the sink. The potential parent with the lowest degree in the graph is selected as the parent for the currently traversed node. Furthermore, we propose two new approaches based on greedy for building a TDMA transmission schedule to perform efficient aggregation on a given tree: WIRES-G and DCAT-Greedy. We evaluate the performance of our algorithms through extensive simulations on randomly generated sensor networks of different sizes and we compare them to the previous state of the art. The results show that both our new scheduling algorithms when combined with our new tree-building algorithm obtain significantly lower latencies than that of the previous best algorithm. wireless sensor networks; data aggregation; minimum latency; degree constraint; transmission scheduling 2016-03-03 国家自然科学基金(61300218); 广东省软科学研究计划项目(142400410179) 李浩光(1982-),男,广东云浮人,硕士,讲师,研究方向:无线传感网、网络算法。E-mail:365073134@qq.com TP 393 A 1006-7167(2017)01-0117-06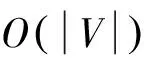

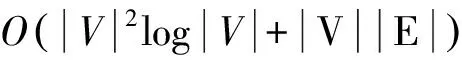
4 仿真结果

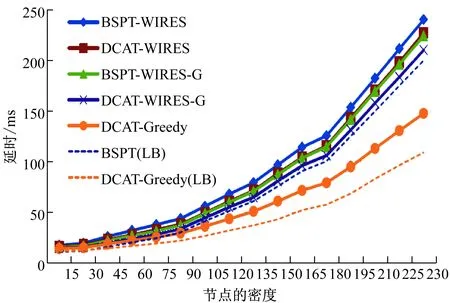
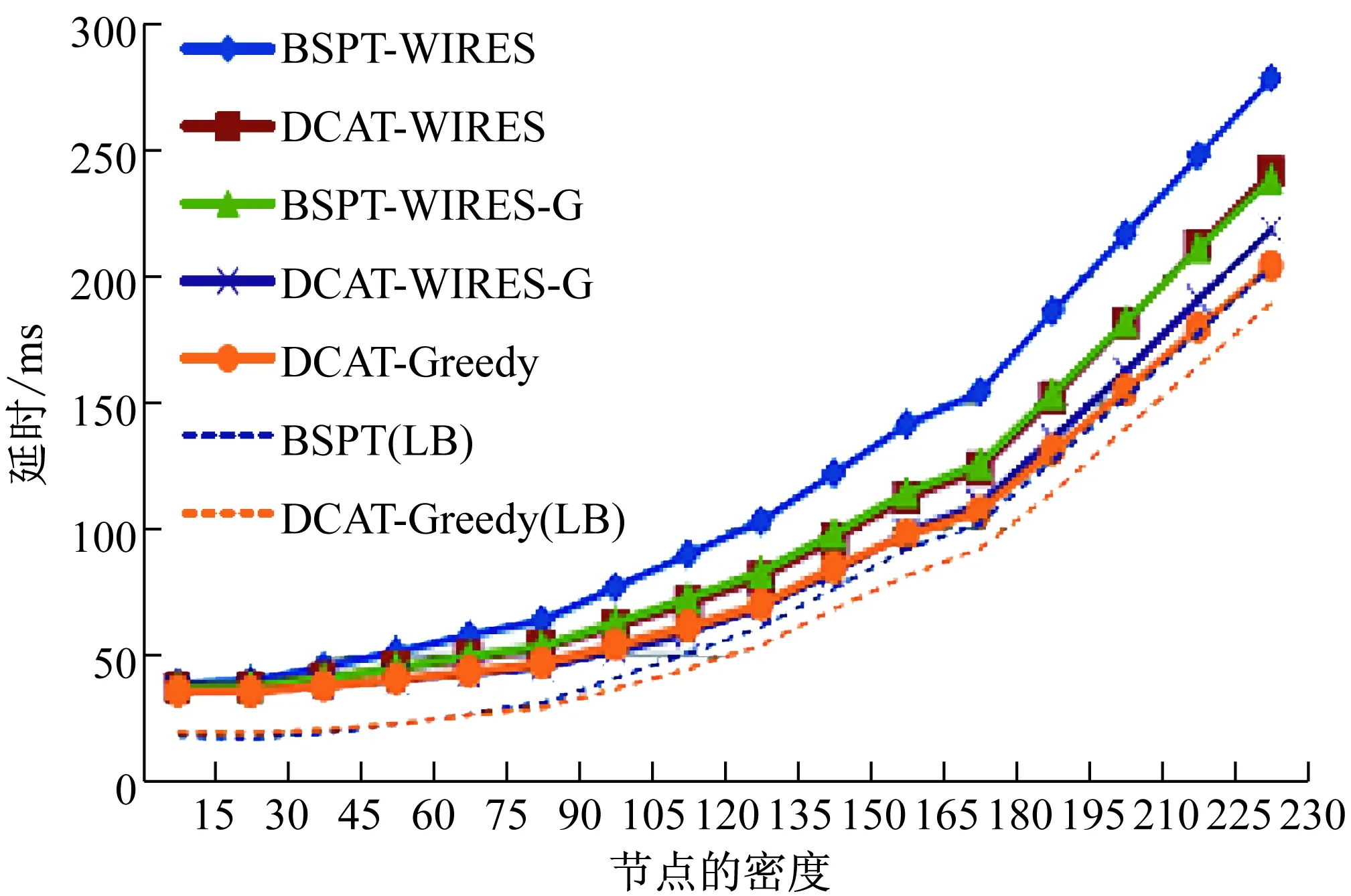
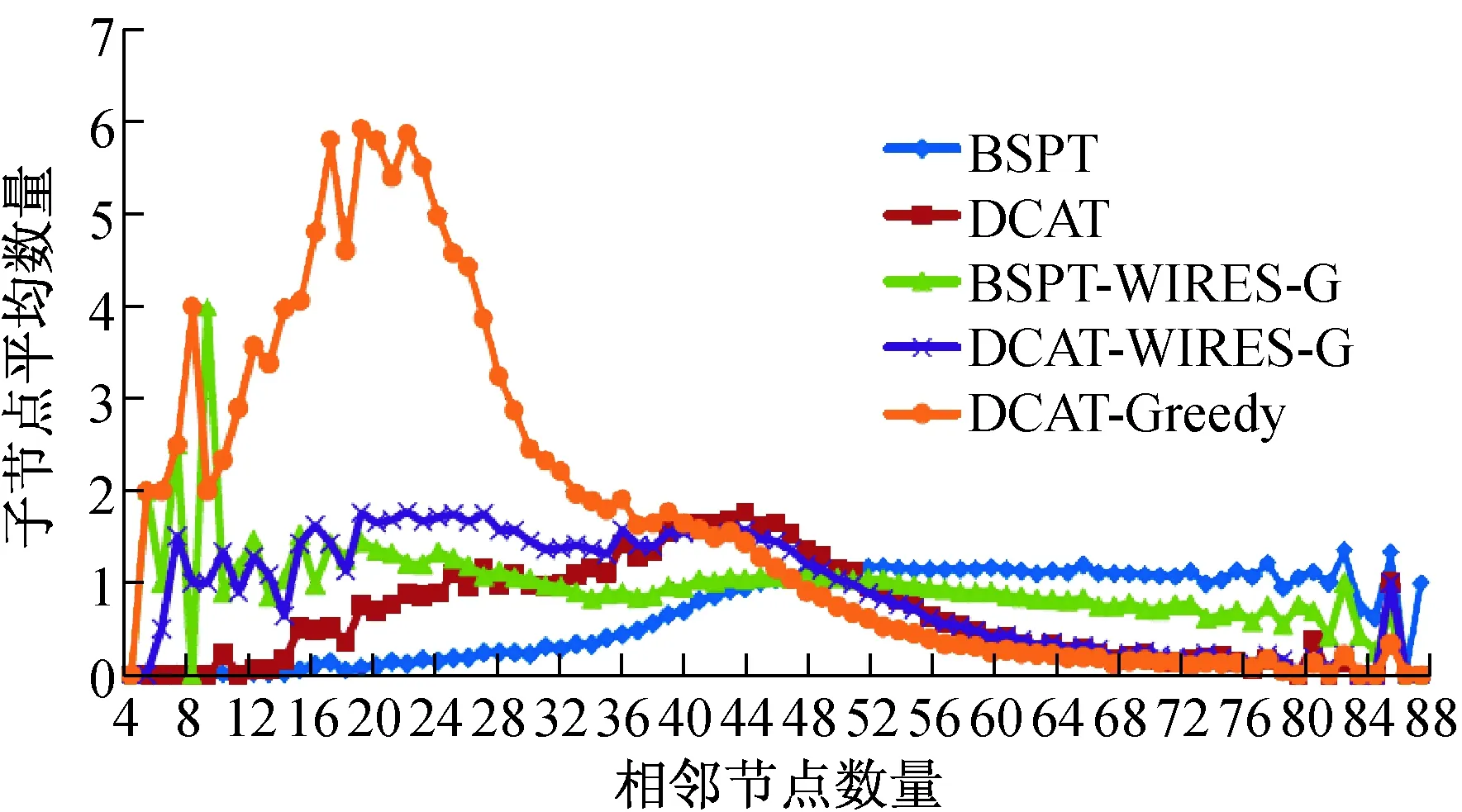
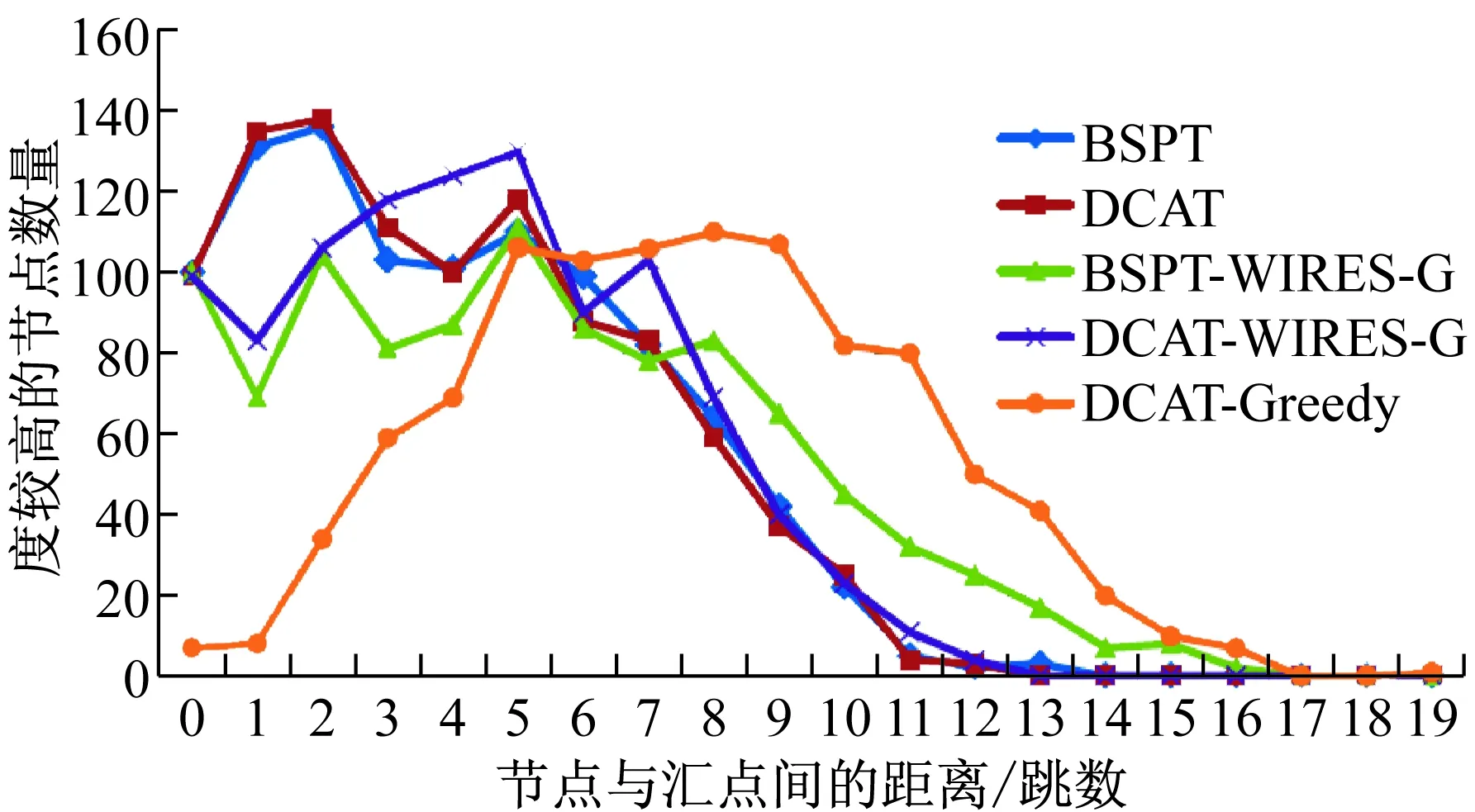
5 结 语

