弧形闸门液压启闭机机构设计方法

刘国民，张步新，耿长兴，冀振亚

（水利部长春机械研究所，吉林 长春 130012）

弧形闸门液压启闭机机构设计方法

刘国民，张步新，耿长兴，冀振亚

（水利部长春机械研究所，吉林 长春 130012）

如何设计弧形闸门液压启闭机机构诸铰链点位置及油缸行程，相关设计规范和手册以及教科书没有论及，其实这是一个既现实又重要的问题。解决该问题需要综合考虑机构运动及力学限定条件。该文从机构运动入手，引入反映机构属性的约束条件，通过求解约束方程获得表征机构的诸参数，在此基础上进一步给出任意位置启闭机油缸以及负载对弧门支铰轴的力矩表达式，从而提供了完整的该类型机构设计方法。文章给出了模拟工程案例以资借鉴。

启闭机；机构；约束条件；油缸；负载

随着液压技术以及传感器技术的不断进步，用油缸提升水利工程弧形闸门已经成为必然选项，然而如何设定机构铰链点位置以及油缸行程是选型设计必须认真权衡的事情。液压启闭机形态通常如图1所示，设计液压启闭机对油缸有两点最起码的要求：首先，能满足运动位置要求，即油缸伸出能使弧门落到底坎上，油缸收缩要保障弧门开度不小于其挡水高度；此外，油缸具有足够的提升力，确保任意位置油缸能提起弧门。事实上满足这两点的机构并非唯一，通过绘图并做适当调整辅以必要的计算可以摸索到一种满足这些要求的方案，然而满足要求并不意味着属于理想方案，理想方案应该是确保任意位置油缸对弧门支铰轴的力矩与负载对弧门支铰轴的力矩之比不小于某一指定值（安全裕度），并且使得满足弧门运动位置的油缸行程达到尽可能小，这是对机构的约束条件。求解满足约束条件的机构是本文确立的目标。

1 机构及油缸行程的确定方法

确定机构及油缸主参数需要综合机构的几何限定条件和力学条件，确切的说由几何限定条件出发求解机构，再从静力学的角度检验机构克服荷载的能力。

1.1 依据机构几何限定条件确定参数

液压启闭机实际上是摆动油缸四杆机构，弧门启闭对应的两极端位置决定了摆臂与机架的摆角差，另外我们可以事先根据机构的受力状况约定油缸完全收缩与完全伸出油缸对支铰轴的作用力矩之比。

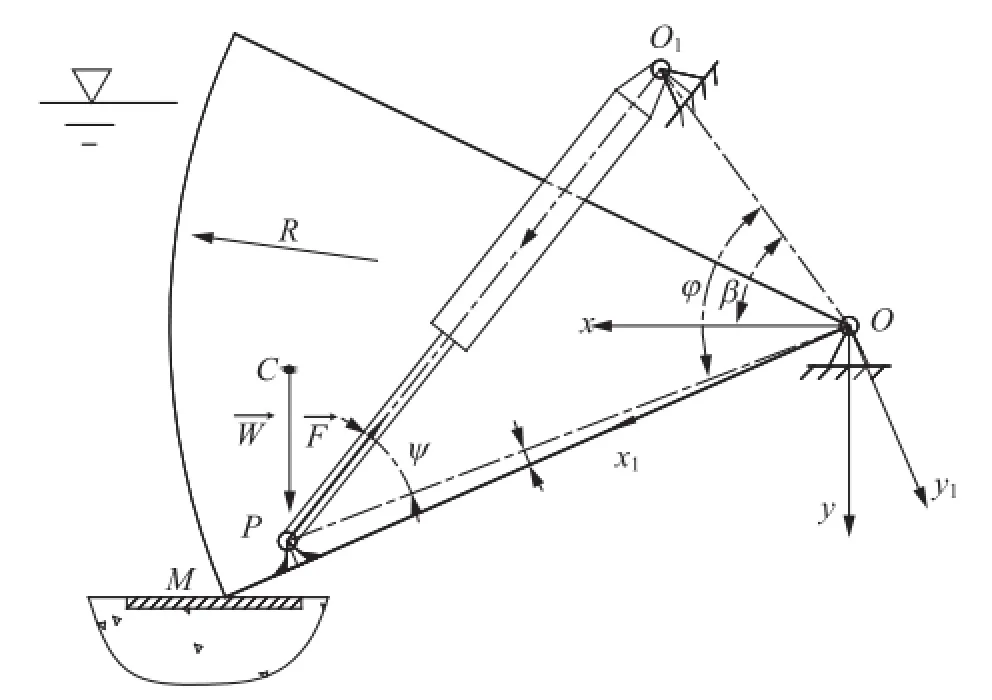
图1 弧形闸门液压启闭机简图

对于任意摆动油缸四杆机构在两极限位置如图2所示。图中：s0—油缸结构长度；x—油缸行程；xr—摆臂；y—机架；φ1—油缸在最短状态摆臂与机架夹角；φ2—油缸最长状态摆臂与机架夹角；ψ1—油缸在最短状态摆臂与油缸轴线夹角；ψ2—油缸在最长状态摆臂与油缸轴线夹角。

对于约束条件我们用数学语言进行解读，关于力矩比可写成

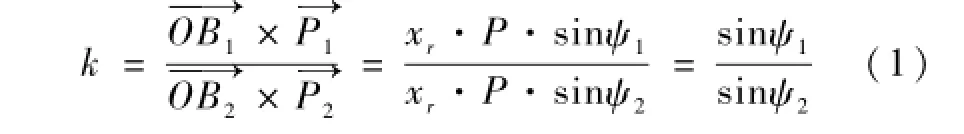
依据三角形边与角的关系，经过一系列变换可将（1）式改写为

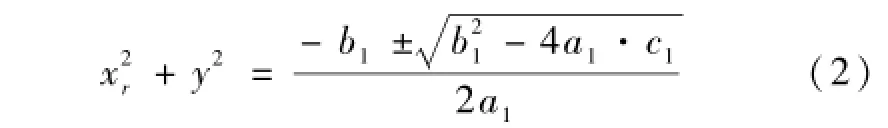
其中：

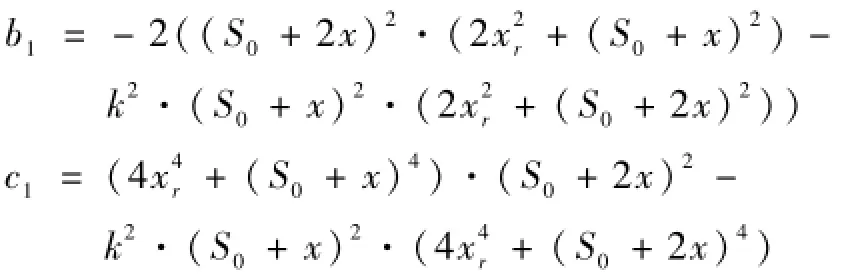
关于另一个约束条件可以写成

类似的利用三角形边与角的关系对（3）式进行改写，可得到关系式

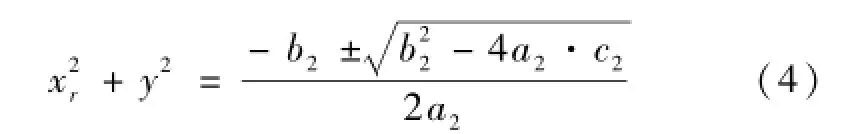
其中：

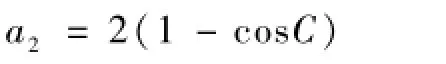
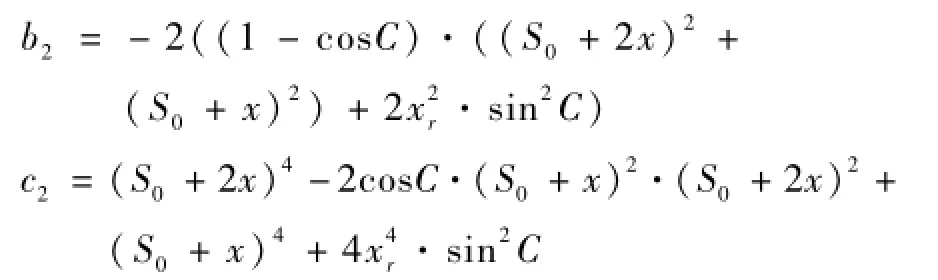
由（2）和（4）联立，可得到方程

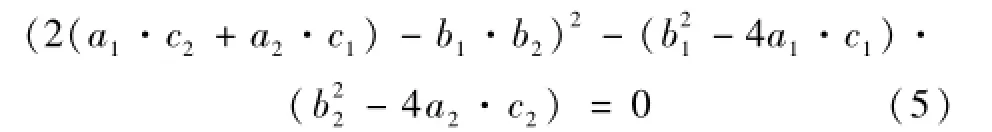
方程（5）实际上是由参数 S0、xr、x、k以及 C复合而成，其中k和C为限定值。设计具体的摆动油缸机构通常的做法是，先根据经验从初选液压缸型号入手查到其结构不变长 S0，另外根据给定空间初选摇臂长度xr，这相当于将S0和xr作为独立参数，则油缸行程x和机架y需要通过解约束方程获得。求解的大致过程是将S0、xr、k以及C代人（5）式，则（5）式成为一个很复杂的关于未知量 x即油缸行程的代数方程。一般来讲该方程有两个正实数解，分别对应大机架小摇臂的摆动油缸机构和小机架大摆臂的摆动油缸机构，就液压启闭机而言属于大摆臂小机架。具体求解先令函数：

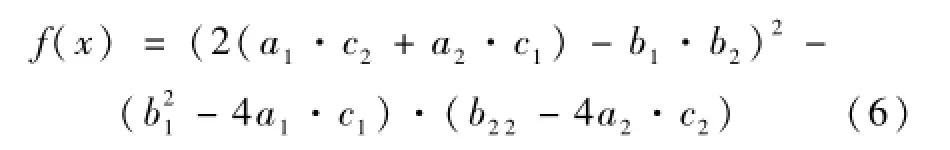
由于真实的机构对应的油缸行程是正实数，因此可以从油缸行程x=0开始依照给定的步长递进，依次计算对应的函数值f（x），一旦发现相邻的函数值符号发生改变即f（xi-1）·f（xi）＜0，说明在区间（xi-1，xi）之间存在方程根，采用Brent方法［4］或借助数学软件MATLAB［5］很容易求得方程数值解x，即满足约束条件的油缸行程。再将x的值代入（2）或者（4）便可很容易得到与其对应的机架y。如果机架y＞xr，则说明获得的解不符合要求，需要继续搜索更大的方程根，当再次遇到f（xj-1）·f（xj）＜0，说明在区间（xj-1，xj）之间存在方程根，再次用前面同样的方法得到的便是满足约束条件的油缸行程x和机架y。

一般来讲上面得到的油缸行程是一个无理数，虽然油缸生产厂可以依用户要求生产定制油缸，却很少见到精度以毫米计的油缸行程。为了妥善处理这一问题我们采用如下办法：选择一个与上面得到的不规则小数表达的油缸行程相近的规则行程（一个规范的数值）替代方程（5）中的x，将摆臂xr看做未知量，则方程（5）就成了未知量 xr的一元方程，用我们前面应用的方法很快求得方程根 xr，以及修正后的机架长度y。

1.2 结合负载条件检验机构作业能力

油缸是否具备克服负载的能力只需将油缸在任意位置其启闭力对支铰轴的力矩和负载对支铰轴的力矩绘制在一张图上便一目了然。如果起升力矩不能满足要求则需调整油缸型号。

无论是油缸对支铰轴的力矩，还是弧门自重对支铰轴的力矩我们一律采用将集中力向其作用点与支铰轴连线的轴线方向和与连线相垂直的两方向分解。因此建立集中力作用线与作用点同支铰轴连线的夹角用油缸瞬时长度表达尤为重要，一旦解决了这个问题意味着油缸对支铰轴的力矩和弧门自重对支铰轴的力矩便迎刃而解。

为了方便描述我们引入两坐标系参照图1，一个是以O为原点的固定坐标系xOy，另一个是以O为原点的转动坐标系x1Oy1。油缸运动铰链点P和弧门重心位置C在转动坐标系x1Oy1中坐标为（xP，yP）和（xC，yC），弧门最低点M在x1Oy1坐标系中的坐标为（R，0），油缸固定铰链点O1在xOy中的坐标 （xO1，yO1）。

从油缸瞬时长度关连的O、P和O1构成的三角形可得到。

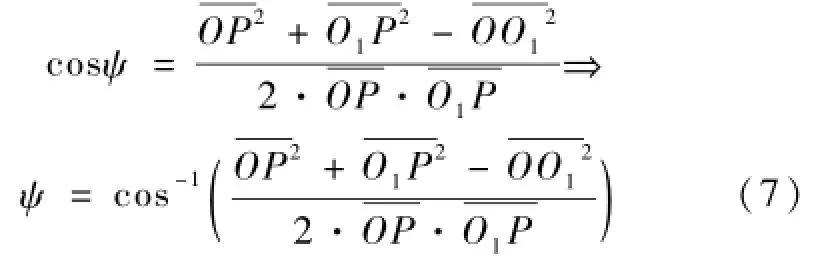
双缸对O点取矩得：

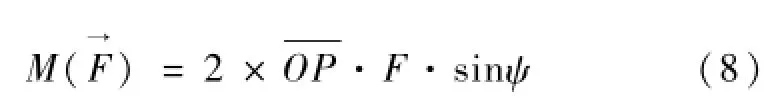
1.2.2 负载对支铰轴的阻力矩

负载对支铰轴阻力矩主要由弧门自重和止水封与侧壁摩擦力构成［2］。

为了得到弧门自重对支铰轴的力矩的表达式，需要先求得OC连线与水平x轴正向夹角。参照图1，依然从O、P和O1构成的三角形可得到

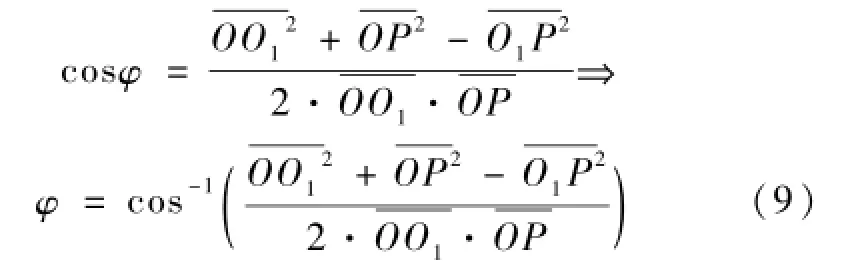
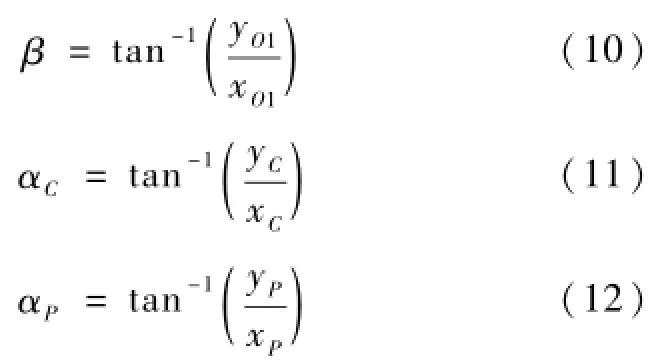
弧门自重对支铰轴的力矩：

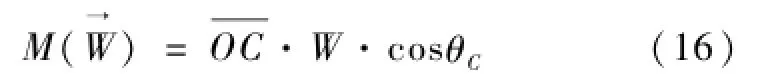
计算止水封对支铰轴的阻力矩从严格意义上说其大小与弧门最低点潜入水面下深度有关，换句话说它也是油缸瞬时长度的函数。设支铰轴线与水面线连线与x轴正向夹角为θ0，参见图3。

图3 水密封摩擦力计算简图

水线面在固定坐标系中纵向座标：

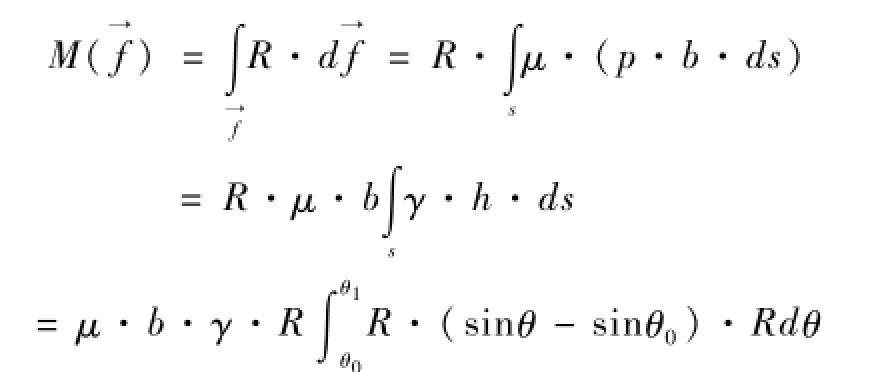
式中，R—弧面曲率半径；μ—止水封与侧壁的摩擦系数；b—受压面止水带宽度；γ—水比重。

将上式积分得：

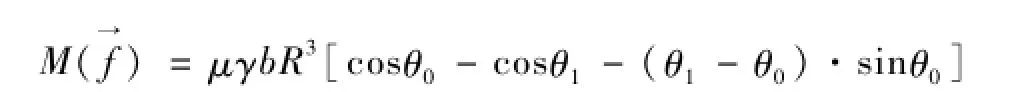
负载的阻力矩，由于止水封左右对称故：

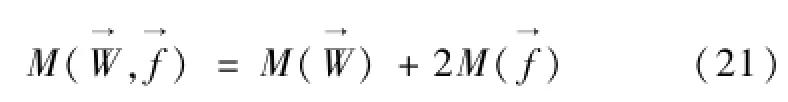
2 模拟案例

设某水库溢洪道工作门采用弧形闸门液压启闭机，标定挡水高度H为15m，工作门重W为150t，试设计弧门启闭机构。

根据《水利水电工程钢闸门设计规范》对于露顶式弧门启闭机弧门曲率半径为R=1.0～1.5H，支铰轴与弧门底坎高差为。故可取弧门曲率半径为挡水高度的1.25倍，即18.75m；支铰轴与弧门底坎高差为0.6倍，即9m。

由于弧门上所有点（包括油缸前铰链点）均相对支铰轴作相同的转动。因此弧门最低点相对支铰轴转过的角度就代表了摆杆的摆角差C，根据以上数值可知：

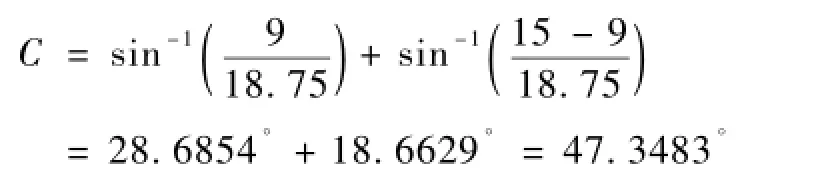
考虑到当弧门被提到挡水高度对应的负载产生的力矩相比弧门位于底坎上要小，故可取油缸完全收缩与油缸完全伸出油缸对支铰轴力矩比：k=0.7；初选QHLY-2×1600油缸，其s0=1900mm；摆臂长xr=17750mm。求解机构油缸行程x以及机架y。

将 C、k、s0、和 xr值代入（5）解得：x= 7472.61mm，y=9729.2mm。

由于油缸行程不规范选择与7472.61接近的规范值x=7500以及C、k和s0值代入（5）求解摆臂长xr和修正后的机架 y。最终解得摆臂长 xr= 17809mm和修正后的机架y=9765mm。

机构确定之后为了后面的计算给出油缸活动支铰P在x1Oy1坐标系中的坐标xP=17695，yP=2005（注：由整体布局确定，要求可以按照前面推导的公式以油缸伸出长度作为自变量计算油缸的启闭力矩和负载阻力矩。

计算启闭力矩和负载阻力矩时先查看油缸样本，QHLY-2×1600标定额定压力p=18.25MPa，缸筒内径D=0.4m，活塞杆直径d=0.22m，止水封与侧壁摩擦系数μ=0.5，止水封宽度b=0.045m，水比重γ=9.8kN/m3。按照前面推导的公式编写MATLAB程序输出部分典型数据以及负载和油缸对弧门支铰轴的力矩曲线如表1和图4。

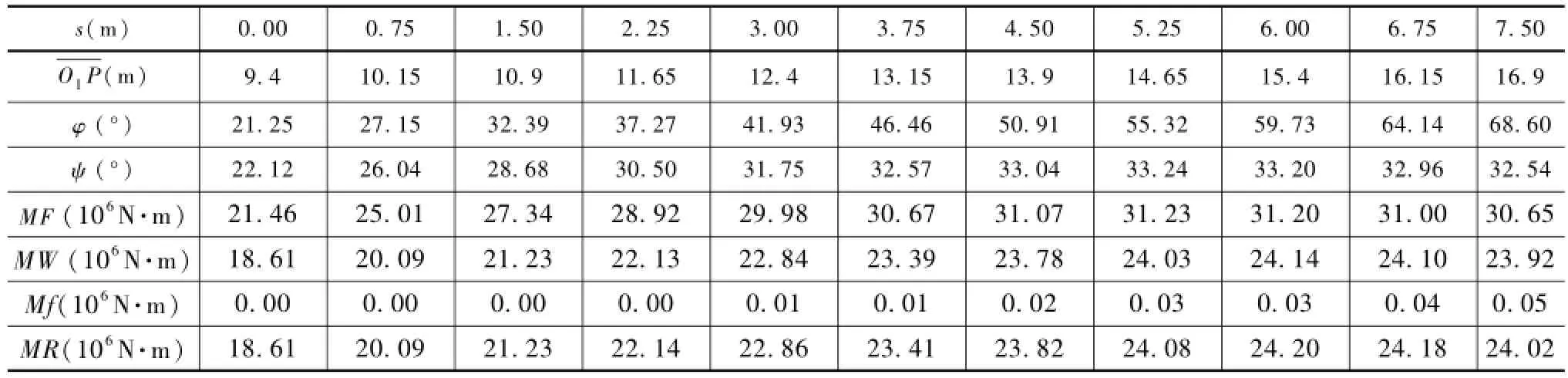
表1 （程序输出数据）

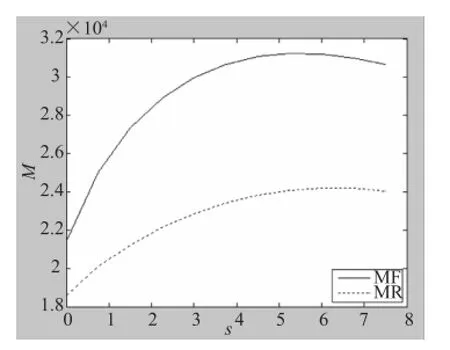
图4 MF和MR随油缸伸缩变化曲线（单位：kN·m）

3 结束语

由如何规范精准设计混凝土输送泵“S”管换向对应的摆动油缸四杆机构导致作者创建了适合于计算机设计任意摆动油缸四杆机构的方法［3］，该方法应用于水工弧形闸门液压启闭机可以免除设计人员为得到满足基本使用要求的机构而反复摸索、调整、计算耗费的繁琐劳动，而且无需借鉴任何类似的机构作为设计切入点，需要补充说明的是采用摸索的方法对应的是一可行域，而摸索到的机构仅仅是可行解集合中元素之一。应用本方法无需走任何弯路便可径直得到理想的满足约束条件的唯一机构，从而为设计弧形闸门液压启闭机机构构建了一条高效快捷途径。

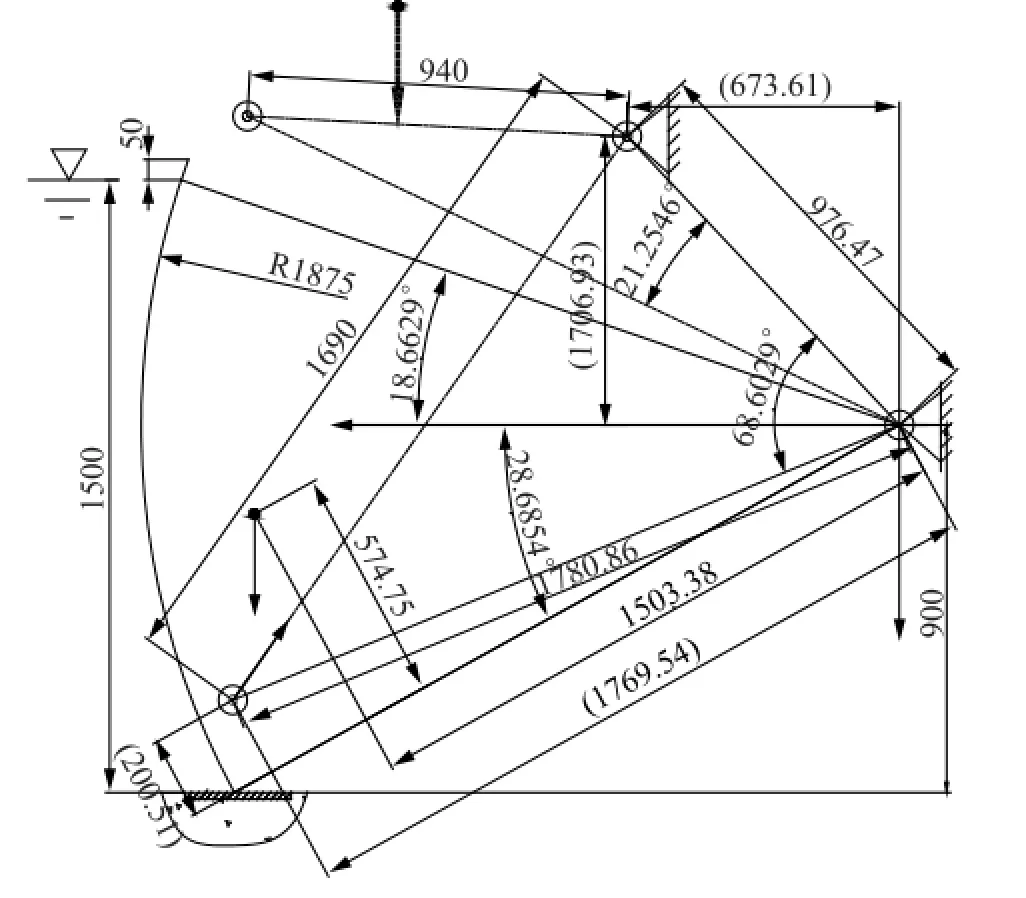
图5 模拟弧门启闭机机构直观几何形线图

［1］SL74-95.水利水电工程钢闸门设计规范［S］.

［2］水电站机电设计手册——金属结构（一）.北京：水利电力出版社，1988.

［3］刘国民，黄海东.摆动液压缸机构设计的一种新方法［J］.工程机械，1998（01）.

［4］阿特金森KE著.匡蛟勋，王国荣，瞿必达译.数值分析引论［M］.上海：上海科学技术出版社，1986.

［5］谢中华，等.MATLAB从零到进阶［M］.北京：北京航空航天大学出版社，2012.

TH137

A

1672-2469（2017）02-0100-04

10.3969/j.issn.1672-2469.2017.02.032

2015-12-30

刘国民（1954年—），男，高级工程师。