大凌河流域水沙特性及变化趋势分析

于国宝

（辽宁省朝阳水文局，辽宁 朝阳 122000）

大凌河流域水沙特性及变化趋势分析

于国宝

（辽宁省朝阳水文局，辽宁 朝阳 122000）

本文对朝阳、大城子、凌海、上窝堡和义县五个地区1991～2010年的水沙观测资料进行分析，得到大凌河流域的水沙特性并建立回归模型。提出基于NEAREST-NEIGHBOR降尺度分析法的水沙特性预测方法，与2011～2015年的实测数据进行比较并对未来20的水沙变化情况进行预测与分析。

大凌河；水沙特性；变化趋势；回归分析

1 概述

本文研究对象为大凌河流域，对朝阳、大城子、凌海、上窝堡和义县五个地区1991～2010年的水沙观测资料进行分析，得到该流域的基本水沙特征。分析发现该流域输沙量的主要影响因素为径流量，而径流量的预测方法较为完善，因此先推求各站径流量与输沙量的回归方程，再对径流量进行预测，最后根据预测得到的径流量计算输沙量。计算结果与2011～2015年的输沙量实测数据进行比较，证明该方法较为精确，可以在实际工作中发挥重要作用，并对研究区域内未来20年内的水沙情况进行了预测分析。

2 径流量与输沙量变化特性

大凌河流域主要位于辽宁省，部分区域位于内蒙古和河北省，总面积 23263km2，发源于建昌市和平泉县，汇入渤海。本流域位于中温带季风气候区，雨水分布不均，洪涝与干旱灾害频繁。选取流域内五个水文站的逐月水文资料，五个水文站分别为朝阳站、大城子站、凌海站、上窝堡站和义县站，其资料选取范围为1991～2015年。其中1991～2010年数据用于率定参数，2011～2015年资料用于检验。使用FORTRAN语言编写程序将逐月水文资料进行数据统计，得到径流量随时间变化情况、输沙量随时间变化情况、以及各站的最大值、最小值、平均值和变差系数，分别如图1、图2和表1所示。

图1为径流量随时间变化情况图，其中横坐标代表时间，纵坐标代表径流量，其单位为亿 m3。由图可见，在1995年前后径流量明显较大，主要是因为这段时期为丰水期，洪涝灾害比较严重。自2000年开始，各站径流量相对较小，说明该流域内各站的径流量时间分布不均匀。各站的径流量值相差较大，即该流域径流量空间分布也不均匀。研究范围内径流量最大的是凌海站和义县站，其最大径流量分别超过45和27亿 m3洪水，径流量较小的为大城子和上窝堡，其最大径流量仅为10亿m3左右。

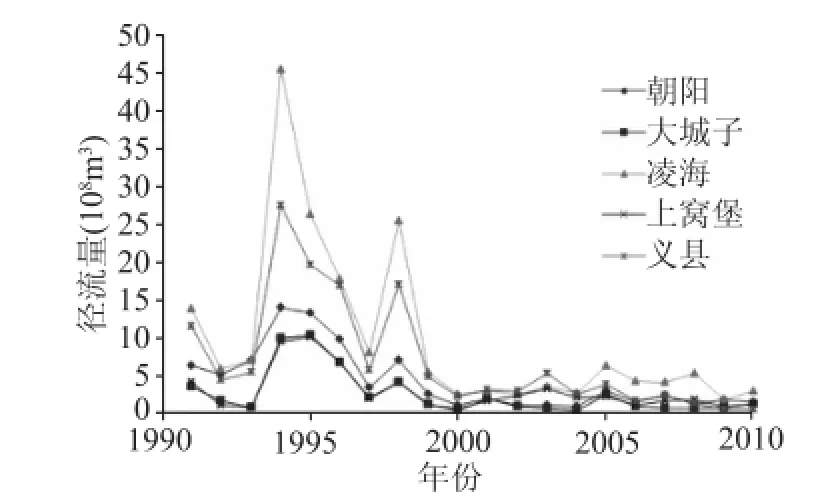
图1 各站径流量随时间变化情况

图2 为输沙量随时间变化情况图，其中输沙量的单位为万t。自2000年后，大凌河流域各站输沙量明显减少，于是在以往的判断中，相关工作者都认为输沙量的较少时因为水土保持措施的实施。但比较图1与图2可以发现，输沙量的变化情况基本与径流量的变化情况保持同步，即在1995年左右的丰水期输沙量较大，而在枯水期则输沙量较小，

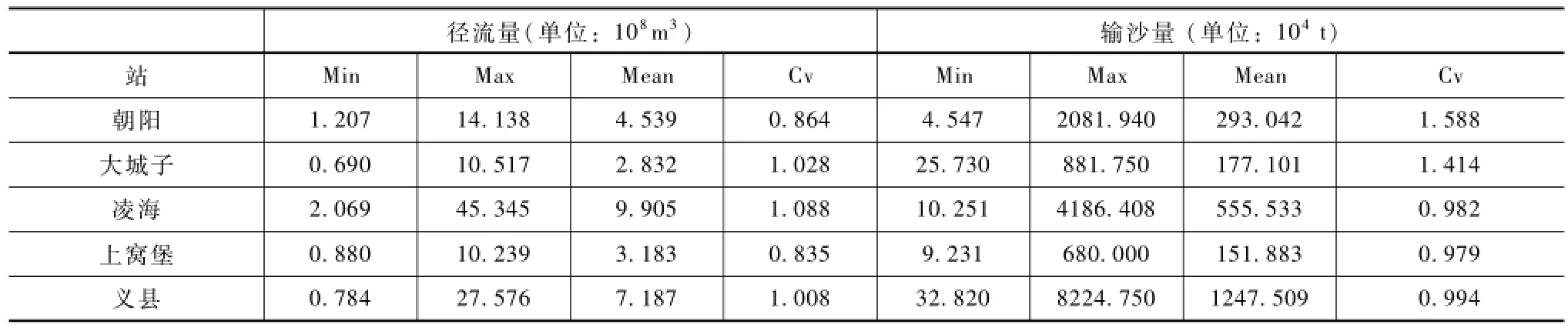
表1 各站径流量与输沙量统计特征

时间分布不均。Mann-Kendell检验法显示大凌河流域的输沙量明显与径流量相关，大凌河2000年后输沙量的减少约80%左右是由径流量的减小所引起的。通过比较还可以发现，输沙量的空间分布同样不均，但相对于径流量的空间分布则较为均匀。因为输沙量的比值可以在一定程度上表示一个地区的水土流失情况，于是可知在输沙量差别不大的情况下，某地区径流量越小则水土流失越严重，即义县的水土流失情况较为严重。

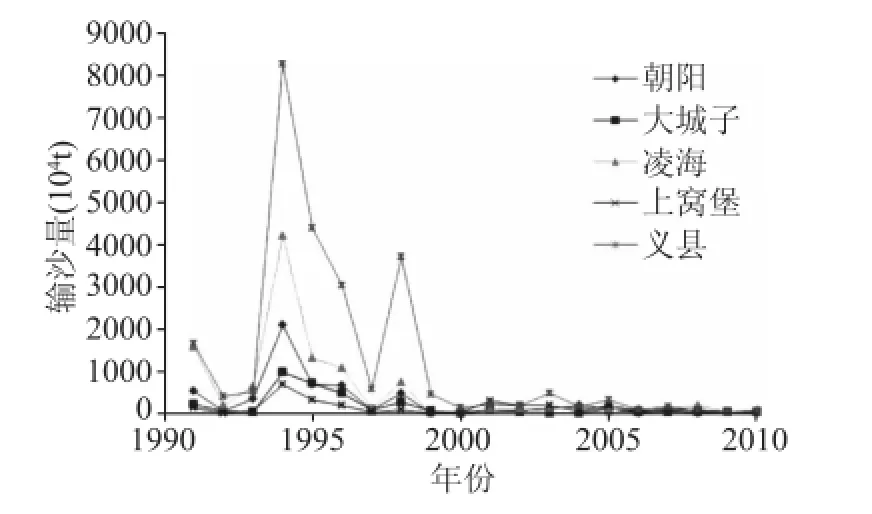
图2 各站输沙量随时间变化情况

表1为大凌河流域各站径流量与输沙量的统计结果，该表格所列数据可以用来对该流域的水沙特性进行量化分析，其中Min代表最小值，Max代表最大值，Mean代表平均值，Cv代表变差系数。整个流域中的径流量最小值为0.690亿 m3，出现在大城子站，说明该地区在枯水期面临的旱情较为严重；径流量最大值为45.345亿 m3，出现在凌海站，说明该地区在丰水期面临的洪涝灾害最为严重；平均值最小的为大城子站，为 2.832亿 m3，说明该地区相对缺水；而平均值最大的为凌海站，为9.905亿m3，说明该地区水资源相对丰富。变差系数可表示数据分布的均匀程度，其计算公式为：

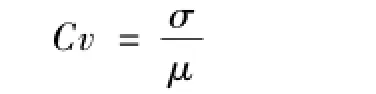
其中σ为各站数据中的标准差，而μ代表数据的平均值。研究区域内的最小变差系数为0.835，出现在上窝堡站，说明该地区径流量时间分布较为均匀，而最大值出现在凌海站，为1.088，说明该地区径流量分布较不均匀，但各站之间的变差系数相差不大，说明该流域内径流量各站的时间分布不均匀性较为平均。

同理可知，平均输沙量最小的为上窝堡地区，为151.883万 t；平均输沙量最大的是义县地区，为1247.509万t。流域内各站输沙量的时间分布不均匀性相对径流量更为分散，其中最为分散的为朝阳地区，其变差系数达1.588，而最为平均的是上窝堡地区，为0.979。各站输沙量的变差系数明显高于径流量的变差系数，说明输沙量的时间分布更不均匀，即径流量增大时，输沙量增大量较大，而当径流量减小时，输沙量减小量也较大，其变化受径流量变化情况的影响较大。

3 水沙相关性及趋势预测

相对于水沙数据解释，水沙特性的预测在实际工作中具有更为重要的应用价值，但这方面的研究却相对较少。由于各流域具有不同的水沙规律，因此不可直接套用已有的经验公式来进行预测。根据传统的分析方法，应该根据前文所得数据进行变化趋势规律，并使用该趋势来计算将来的水沙特性，但该方法的精确性却很低，应用价值较低。本文基于Nearest-Neighbor法、结合大凌河流域径流量历史数据将CMIP5环流模拟结果进行降尺度分析，得到大凌河流域各站的径流量预测值。根据大凌河径流量与输沙量历史数据进行回归分析，得到两者回归方程，再利用该方程计算输沙量。由于该方法更符合物理规律，因此该方法将比传统的纯统计方法更为准确。

通过回归分析，得知输沙量与径流量主要呈二次多项关系，其回归方程如下：

朝阳站：S=7.001x2+5.940x

大城子站：S=4.088x2+39.313x

凌海：S=1.412x2+23.589x

上窝堡：S=0.047x2+46.038x

义县：S=9.500x2+35.242x

式中x代表径流量，S代表输沙量。

为验证本文提出方法的准确性，首先对 2011～2015年的输沙量进行预测，并与实测值进行比较。对比较结果进行无量纲化处理，从而可以直观的得出该方法的精确度，如图3所示。图3中横坐标为年份，纵坐标为精确系数，该系数为计算值与实测值的比值，当该值大于1时说明计算值高估输沙量，而低于1时说明计算值低估输沙量，而其范围则表示误差范围。可见，该方法的精确度达80%以上，高于传统的预测方法，因此可以在实际工作中得到应用。

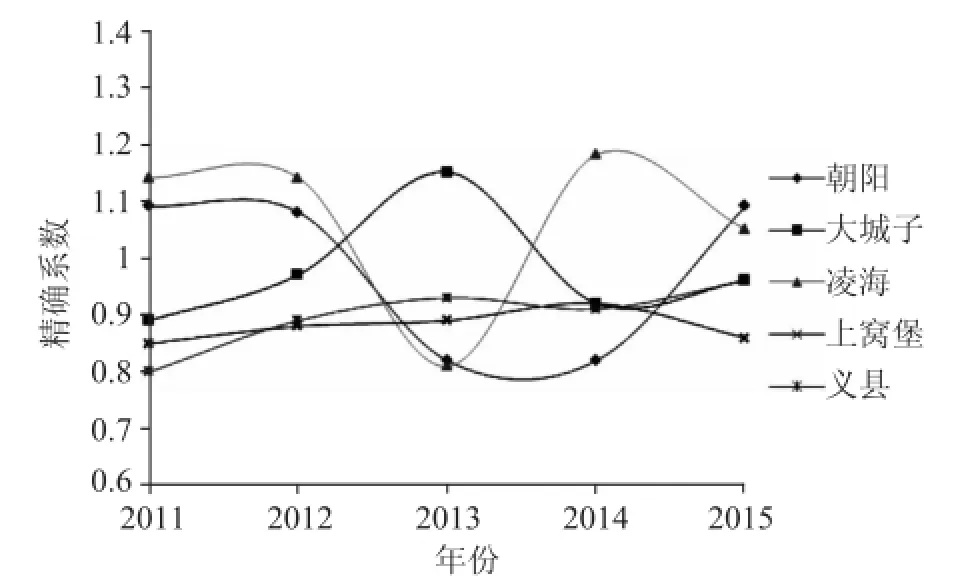
图3 预测精确度分析图

使用本文所提出的方法对大凌河流域未来20年内的径流量和输沙量进行了预测，结果分别如图4和图5所示。

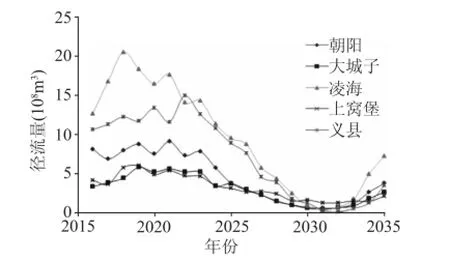
图4 径流量预测结果

由图4所示，在短期内，大凌河流域可能将进入丰水期，径流量和输沙量都将有所增加，其中最大径流量可能将达到20亿m3，而最大输沙量将达到2500万t。之后该流域将重新回到枯水期，径流量与输沙量在2030年左右达到最低值，并开始重新上升。该方法中的不确定因素为代表性浓度途径（RCP），在 CMIP5模拟结果中，有 RCP26， RCP45，RCP60以及RCP85四种不同的情况，而本文所采用的是四种情况的平均值，由于气候变化的不确定性，该方法也需要根据实际气候变化情况不断修正、改进，从而得到更为精确的结果。

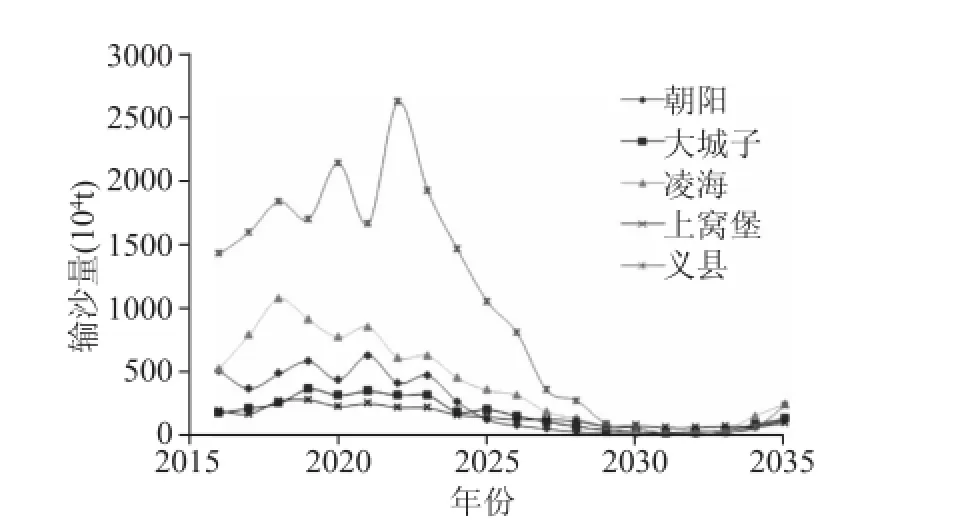
图5 输沙量预测结果

4 总结

利用大凌河流域朝阳、大城子、凌海、上窝堡和义县五个地区1991～2010年20年的水沙观测资料得到了该流域的水沙特性，Mann-Kendell检验结果显示该流域的输沙量明显与径流量相关，并利用回归分析技术得到各站输沙量与径流量的回归方程。本文基于Nearest-Neighbor法、结合大凌河流域径流量历史数据将CMIP5环流模拟结果进行降尺度分析，得到大凌河流域各站的径流量预测值，再利用本文所得回归方程得到各站输沙量预测值。利用2011～2015年的实测值对本文方法的精确度进行了分析，证明该方法较为精确，并用该方法得到了未来20年内大凌河流域的水沙变化情况。

［1］刘鑫.大凌河流域径流演变规律分析［J］.水土保持研究，2015（02）：165-170.

［2］王世钧.渭河上游水沙特性变化及其规律研究［J］.水利规划与设计，2013（09）：8-10.

［3］王光谦.河流泥沙研究进展［J］.泥沙研究，2007（04）：64-81.

［4］郭维东，孙丽玲，等.大凌河中下游输沙特性分析［J］.中国农村水利水电，2015（04）：82-89.

［5］霍庭秀，罗虹，等.黄河中游河龙区间水沙特性分析［J］.水利技术监督，2009（05）：13-15.

［6］许全喜，石国钰，陈泽东.长江上游近期水沙变化特点及其趋势分析［J］.水科学进展，2004（04）：420-426.

［7］吴俊秀，郭清.大凌河流域MIKEBASIN水资源模型［J］.水文，2011（02）：70-75.

［8］吴俊秀，张晓红，车延路.综合治理对大凌河流域泥沙影响分析［J］.东北水利水电，2005（02）：31-32.

TV143

B

1672-2469（2017）02-0041-03

10.3969/j.issn.1672-2469.2017.02.015

2016-05-16

于国宝（1983年—），男，工程师。