Secure Spectral-Energy Efficiency Tradeoff in Random Cognitive Relay Networks
Bing Wang, Kaizhi Huang,*, Xiaoming Xu, Yi Wang,2
1 National Digital Switching System Engineering and Technological Research Center, Zhengzhou 450002, China
2 School of Electronics and Communication Engineering, Zhengzhou University of Aeronautics,Zhengzhou 450046, China
I. INTRODUCTION
IMT-2020 (5G) Promotion Group points out that 5G aims to achieve all-spectrum access and seamless wide-area coverage in the 5G white paper [1]. All-spectrum access means that we need to exploit variety of spectrum resources,including paired and unpaired, licensed and unlicensed, contiguous an non-contiguous frequency bands [2]. Recently, cognitive radio(CR) [3] has become a hot topic for academia and industry, because it allows unauthorized users (secondary users) to dynamically access the licensed spectrum, thus improving the spectral efficiency (SE). As for seamless wide-area coverage, relay technology is an effective way in enhancing transmission reliability, system capacity, and coverage area [4, 5]. The above two reasons prompted the cognitive relay network to be still a research hotspot in the future 5G network. However, due to the open nature of wireless channels, information security has always been an issue that we cannot avoid in 2G, 3G, and 4G networks, and will be still a research focuses in 5G networks definitely[6]. Compared with traditional security threats caused by the open nature of wireless channels, cognitive relay networks have their own specific issues of security. On the one hand,cognitive relay networks allow unauthorized users to dynamically access the licensed spectral which increases the security threats. On the other hand, the introduction of relays increases the chance of malicious nodes intercepting the private information, which makes the security threats more severe.
In order to prevent the confidential information from overhearing, physical layer security (PLS) techniques [7, 8] have attracted ever-increasing attention since PLS can not only directly achieve information security by exploiting the characteristics of wireless channel [9, 10], but also be used to protect the security of private key distribution which can be regarded as a supplement to traditional cryptography [11]. PLS in cognitive relay networks has been extensively investigated in the context of performance analysis [12], signal processing and resource allocation [13], etc.Nevertheless, most of the existing works on the PLS in cognitive relay networks ignored the energy efficiency (EE) accidently or not.
With the explosive growth of mobile data traffic and rapidly rising energy price, network designers have to consider the economic and environmental costs [14]. In this direction,although the existing systems are mainly designed with high target values for SE, the academia and industry are now showing greater interest in improving EE [15, 16]. [15] studied EE optimization by adjusting the training duration, training power and data power under the constraint of total transmit SE and EE requirement for the user. A secrecy EE maximization problem was considered in [16] where a secondary source communicates with a secondary destination via a multi-antenna relay in the presence of an eavesdropper.
From the above researches, it is found that there already have a number of papers considering SE maximization or EE maximization in cognitive relay networks. However, optimum EE and SE are not always achievable simultaneously [17-20]. Zhang et al. [17] developed a general framework to evaluate the tradeoff between EE and SE in three typical cognitive radio networks modes: underlay, overlay and interweave. Based on the proposed framework,an optimal EE is deduced as the function of SE. Taking account of the unplanned nature of the future wireless networks, SE and EE tradeoff analysis was studied using stochastic geometry in [18-20]. Rao et al. [18] developed a framework for analyzing the SE and EE of a 2-tier heterogeneous cellular network consisting of macro and femtocell base stations operating under a spectrum sharing scenario.Tsilimantos et al. [19] introduced a simple theoretical framework for studying the achieved SE and EE tradeoff in cellular networks.Nevertheless, secrecy-oriented SE and EE performances have been rarely discussed in the above works. Since eavesdroppers are usually passive, eavesdropper’s channel state information (CSI) is not available which makes the tradeoff relationship between secrecy-oriented SE and EE more complicated. Taking security into consideration, Xu et al. [20] developed a framework to jointly optimize the secure SE and EE in cognitive radio networks through condensing the secure SE and EE into a single utility function with a tradeoff factor.
However, to the best of our knowledge, no prior work has accounted for secure SE and EE when designing cognitive relay networks.The introduction of relay nodes introduces both opportunities and challenges for cognitive radio networks. Opportunities come with the introduction of relay nodes enhancing the transmission reliability, system capacity, and coverage area. The challenges refer to that(i) the introduction of relays gives a second chance for malicious nodes to intercept security information, which makes the security threats more severe and the secrecy-oriented SE and EE tradeoff analysis more complex;(ii) the introduction of relays needs extra power consumption, which makes the analysis of secure EE more complex than the traditional cognitive radio networks. Specifically, the difficulty lying in the challenges is how to sched-ule the resources (i.e., transmission power or intensity) of relays to improve the secure SE and EE tradeoff.
Motivated by the above considerations as well as the demands for security and green communications in the future cognitive relay networks, we focus on secure SE and EE tradeoff in cognitive relay networks in this paper, and aim to answer the question: how to schedule the resources (i.e., transmission power or intensity) of relays to improve the secure SE and EE tradeoff of primary network. The major contributions of this paper are summarized as follows:
1) We develop a framework to analyze the random cognitive relay networks where the primary, secondary and eavesdropper nodes are randomly distributed according to Poisson point processes. Specifically, opportunistic relay selection policy is introduced where each primary transmitter communicates with the primary receiver with the help of a secondary user as a relay. Then, the general expressions for the connection outage probability and secrecy outage probability of the typical links in the primary network and secondary network are given. Based on the outage probability results, we evaluate both the secure SE and secure EE of the primary network. It is demonstrated that both of the secure SE and the secure EE increase first then decrease with the increase of relay transmission power or potential relay density. However, the secure SE and the secure EE can not achieve optimal at the same transmission power (or density)which implies the tradeoff between the secure SE and the secure EE.
2) We conduct a secure SE and EE tradeoff analysis to jointly optimize the secure SE and EE. Similar with the most existing works [18][20], we condense the secure SE and EE into a single utility function with a tradeoff factor.Our design encompasses secure SE optimization problem and secure EE optimization problem as special cases. Considering the non-concave feature of the objective function,an iterative algorithm is proposed to improve the secure SE and EE tradeoff. Furthermore,this paper gives a guidance on how to schedule the transmission power and potential density of relays to enhance the secure SE and EE tradeoff of primary networks. Numerical results show that our opportunistic relay selection policy is always superior to random relay selection policy. It is also found that our opportunistic relay selection policy outperforms the conventional direct transmission policy when faced with small security threat (i.e., for smaller eavesdropper density). Consequently, to further improve the secure SE and EE tradeoff, we should adaptively select different policies based on the eavesdropper environment.
The remainder of this paper is organized as follows. In Section II, the system model is presented. In Section III, we investigate the connection outage probability, secrecy outage probability, secure SE and EE, respectively.We formulate the secure SE and EE tradeoff problem to jointly optimize the secure SE and EE and give an iterative algorithm to improve the secure SE and EE tradeoff In Section IV. The numerical and simulation results are shown in Section V and Section VI concludes the paper.
II. SYSTEM MODEL
2.1 Network descriptions
We consider an underlay random cognitive relay network as depicted in figure 1. Each primary transmitter communicates with the primary receiver with the help of a secondary user as a relay using DF (decode-and-forward)relaying protocol. The location of primary transmitters (PU-Txs), secondary transmitters(SU-Txs) and eavesdroppers are modeled as independent homogeneous Poisson point process (HPPP) ΦP, ΦSand ΦEwith densities λP, λSand λE, respectively. We consider the case that the density λSis larger than λP,which is very common in heterogeneous cellular networks where the number of pico base stations is larger than macro base stations [21].The secondary network shares the spectrum with the primary network, the effect of thermal noise can be ignored and signal-to-interference ratio (SIR) is used [22]. Each node in the random cognitive relay networks is equipped with a single antenna.
The bipolar network model is considered like [23], where each transmitter is assumed to have an intended receiver at a fixed distance.Assume that each PU-Tx and SU-Tx transmit information with the same power PPand PS,respectively. Each PU-Rx is at a distance lPfrom the corresponding PU-Tx with isotropic directions. We assume that there is no direct link between PU-Rx and PU-Tx. Each SURx is at a distance lSfrom the corresponding SU-Tx in a random direction. Specially, it should be pointed out that although the analysis of bipolar network model based on the fixed transmission distance, it can be extended to the case where the transmission distance obeys a certain distribution of random variables [20]. The wireless communication channel is modeled as a path-loss plus quasi-static Rayleigh fading channel. Denote the Rayleigh fading channel gain and the distance between the node a and the node b as Gaband lab,respectively. We assume that transmitter has the perfect CSI of the legitimate link while the eavesdropper’ CSI is unavailable at the legitimate transmitters.
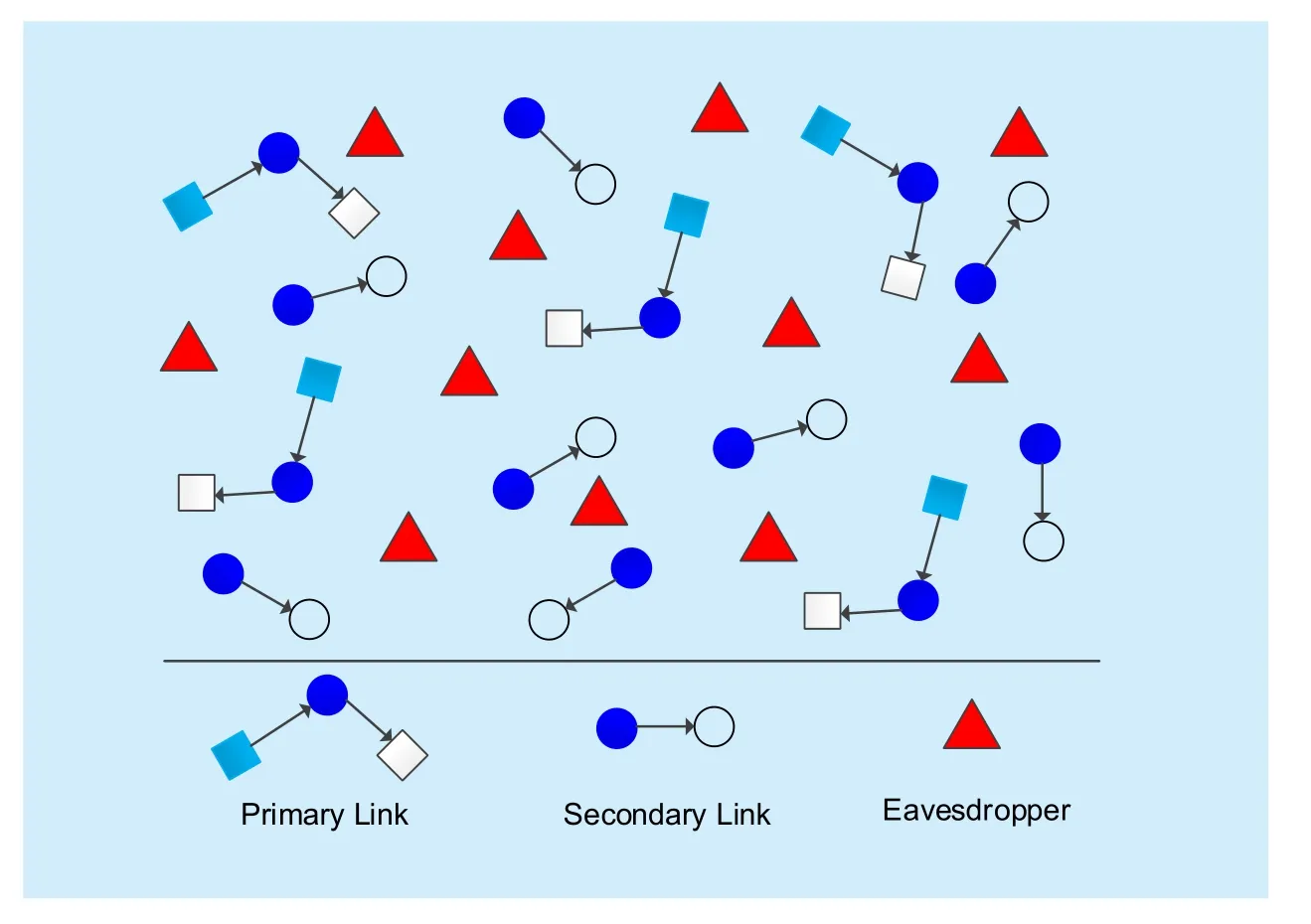
Fig. 1 An illustration of a cognitive relay network where each primary transmitter communicates with the primary receiver with the help of a secondary user as a relay
We assume that the non-colluding eavesdroppers intend to overhear the data transmissions in the primary network. To ensure confidential information security, the wiretap code is adopted at PU-Txs for message transmissions. Considering that the difficulty of codebook designing and any instantaneous CSI is not available for PU-Txs, the codeword transmission rates Rt,Pand confidential information rate Rm,Pare assumed fixed over time[21].
2.2 Opportunistic relay selection
Different from the traditional opportunistic relay selection (ORS) policy which needs extra relay to complete communication [5], we select relay from secondary user in our ORS policy. Through this policy, primary users can complete the normal communication on the one hand, secondary user which doesn’t be selected as relay gets the opportunity to communicate on the other hand, wherein the mutual benefit between primary users and secondary users is realized. The two phases transmissions is proposed as follows:
1) Phase 1-: PU-Tx first broadcasts the training sequence, the best relay is selected from SU-Txs which can decode data from PUTx correctly and has the highest instantaneous signal strength between SU-Tx and PU-Rx.Then, PU-Tx transmits its encoded signal,the best relay is listening while other SUTxs which haven’t been selected as relays are transmitting their own information to SU-Rxs.
2) Phase 2-: Relay forwards the re-encoded signal to the PU-Rx while other SU-Rxs are transmitting their own information to SU-Rxs.
It should be noted that this relay selection policy only considers the instantaneous signal strength between SU-Tx and PU-Rx due to the fact that eavesdropper’ CSI is unavailable for us. If we can get the eavesdropper’ CSI,selecting the relay which achieves a good tradeoff between data delivery (from SU-TX to PU-Rx) and secure transmission will be a better way, which can be regarded as one of the future work.
2.3 Performance metric
1) Connection Outage Probability (COP):COP is defined as the probability that the channel capacity from the transmitter to the receiver is less than the transmission rate. Define a threshold SIR value for connection outage of the typical primary link aswhere Rt,Pis the transmission rate of PU-Txs.Similarly, the threshold SIR value for connection outage of the typical secondary link is defined as θco,S.
2) Secrecy Outage Probability (SOP):SOP is defined as the probability that the channel capacity from the transmitter to the eavesdropper is larger than the rate incrementDefine a threshold SIR value for secrecy outage of the typical primary link as θso,P.
3) Secure Spectrum Efficiency: Secure SE is defined as the average secrecy rate at which the confidential messages are reliably and securely transmitted over 1 Hz nominal bandwidth and over an area of 1 m2just like [20,24].
4) Secure Energy Efficiency: Secure EE is defined as average secrecy rate at which the confidential messages are reliably and securely transmitted over 1 Hz nominal bandwidth while consuming 1 W power just like [17, 25].
III. PERFORMANCE ANALYSIS
In this section, we derive the expressions for connection outage probabilities (COPs) for the primary network and secondary network,the secrecy outage probability (SOP) for the primary network. Then, the expressions for secure SE and secure EE are given based on the outage results.
3.1 Connection outage probability
We first derive the COP of the primary network to evaluate the reliability performance of the network. In this work, we assume that every PU-Tx can select a unique relay to help the transmission since SU-Tx’s density λSis larger than PU-Tx’s density λP. The distribution of relays also follows a HPPP ΦSwith spatial density λRaccording to the displacement theorem of a HPPP [26].
In the DF relaying protocol, the secrecy data transmission of each primary pair is divided into two phases. Since relays selected from SU-Txs can decode the data from PUTxs successfully in the first stage, the COP of the first stage is not considered and only the second phase’s COP is considered. Those SUTxs in ΦSthat succeed in decoding the data from PU-Tx u0constitute the decoded set ωu0. We first provide the distribution of ωu0in the following proposition.
During the ORS process, the typical PUTx u0first broadcasts its signal while the best relay set is listening. The instantaneous SIR received by a relay r in the first phase is given by
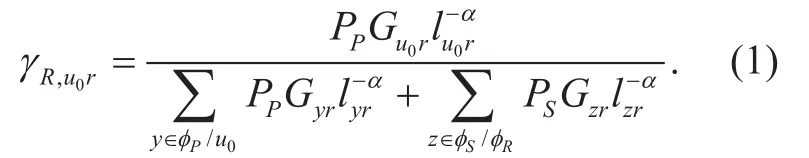
Proposition 1: In the close area A⊂R2, the average number of relays which can decode the data from u0successfully is (2) shown in the bottom at this page.
Proof: Please see Appendix A.
From Proposition 1, we note that the intensity λSof secondary user is a key factor influencing the average number of relays which can decode the data from PU-Txs successfully,in other words, λSrepresents the potential relay density.
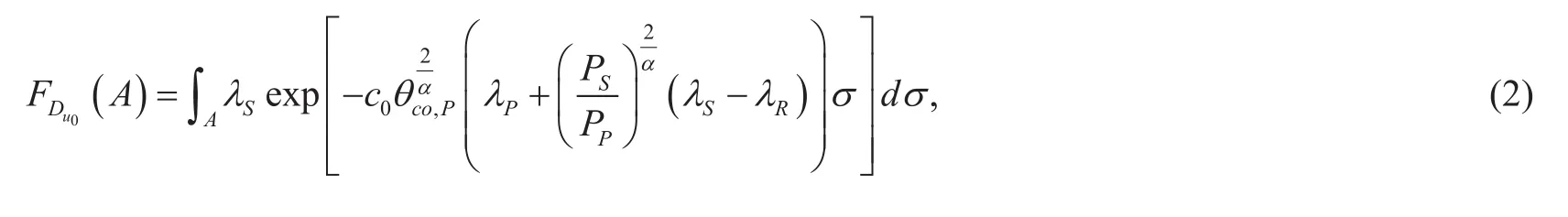
In the second phase, the best relay rj∈uω0which has the highest instantaneous signal strength of the r−v0link forwards its decoded and re-encoded signal to v0. Mathematically,the best relay can be formulated as
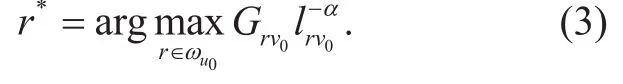
Since the best relay is selected from SUTxs, the transmission power of relays and SUTxs is equal, i. e., PR=PS. Thus, the instantaneous SIR received at v0in the second phase is given by
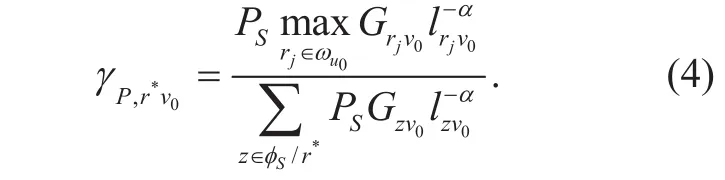
Thus, the COP of typical relay link in the primary network is given by
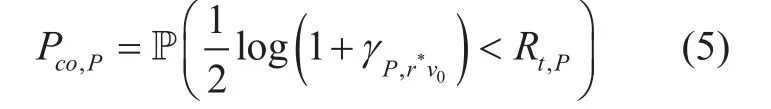
Considering the random distributions of SU-Txs, decoded set, Pco,Pin (5) can be further expressed as (6) shown in the bottom at this page.
Since it is difficult to get the closed form of Pco,P, an upper bounds of Pco,Pis shown in proposition 2.
Proposition 2: An upper bound on the COP of the typical relay link in the primary network is given by (7) shown in the bottom at this page.
Proof: Please see Appendix B.
Proposition 3: The COP of the secondary network in the first phase and second phase are given by (8) and (9), respectively. Detail proof is similar with [20], which is omitted here.
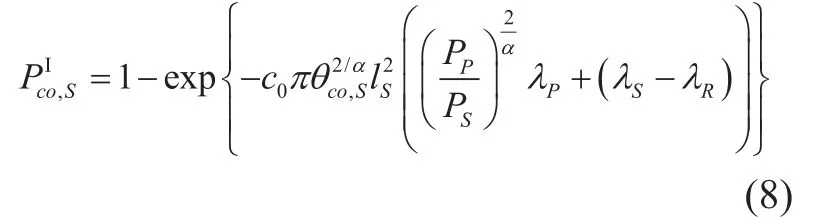
and
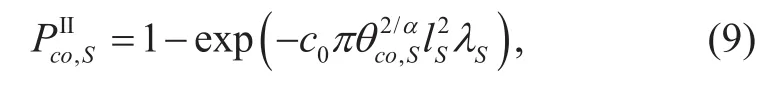
3.2 Secrecy outage probability
Then, we derive the SOP of the typical link in the primary network to evaluate the security performance. The instantaneous SIR received by a eavesdropper e in the first phase is given by
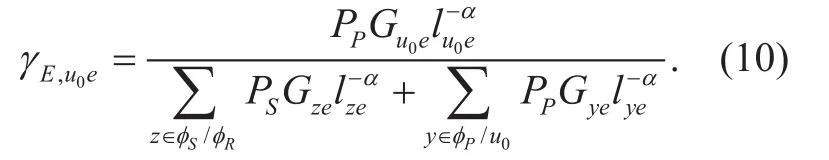
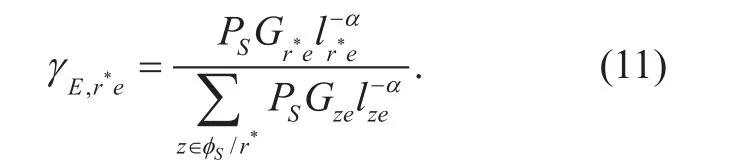
The most malicious eavesdropper that has the largest SIR of the two phases is chosen as eavesdropper’s SIR
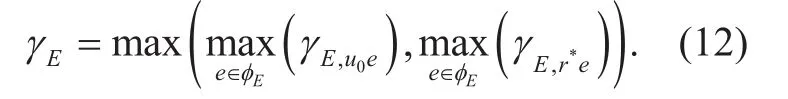
Thus, the SOP of typical relay link in the primary network is given by
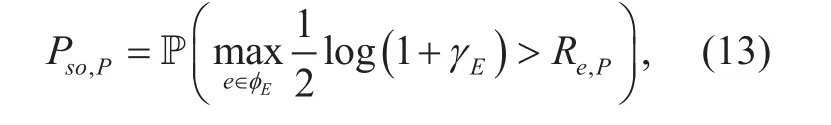
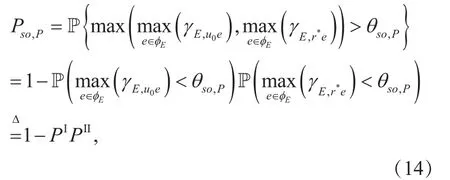
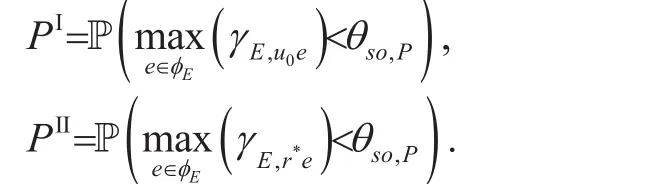

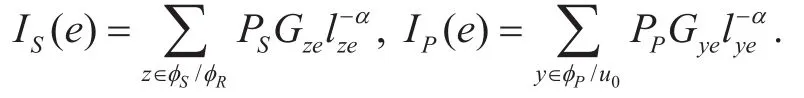
Using the generating function of the PPP φE[27], (15) can be further expressed as (16)shown in the bottom at this page.
Since it is difficult to exactly express PIin a closed form, we look for an analytical bound on the SOP. Jensen’s inequality gives a lower bound on PIas (17) shown in the bottom at this page, where redenotes the distance between the PU-Tx u0and eavesdropper e.Then, by directly evaluating the integral in(17), the lower bound of PIis obtained as
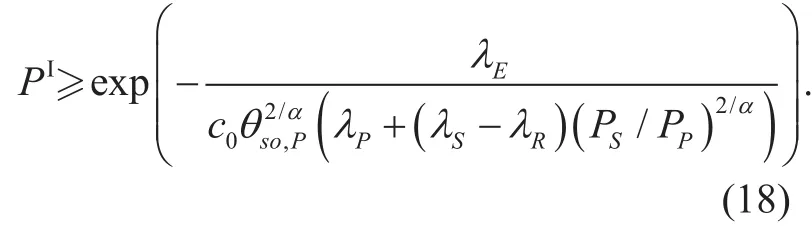
Similarly, the lower bound of PIIis obtained as
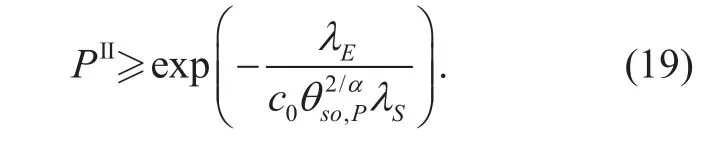
The upper bound on the SOP of the typical relay link in the primary network is given by(20) shown in the bottom at this page.
Remark 1: From the analysis of COP and SOP of the primary network, it is found that COP is an increasing function of PS(Sλ) while SOP is a decreasing function of PS(Sλ). In other words, there exists a security-reliability tradeoff introduced by the transmission power PSand the potential density λSof relays.
3.3 Secure SE Analysis
Here, we note that the secure SE in (21)takes both reliability and security into consideration. From Remark 1, we know that the transmission power PSand the potential density λSof relays play an important role in the tradeoff between security and reliability. Thus,in order to maximize the secure SE, PSand λSshould be designed carefully.
3.4 Secure EE analysis
Since transmitters take the main power consumption in the cellular networks, the receivers’ consumed power is not considered here.
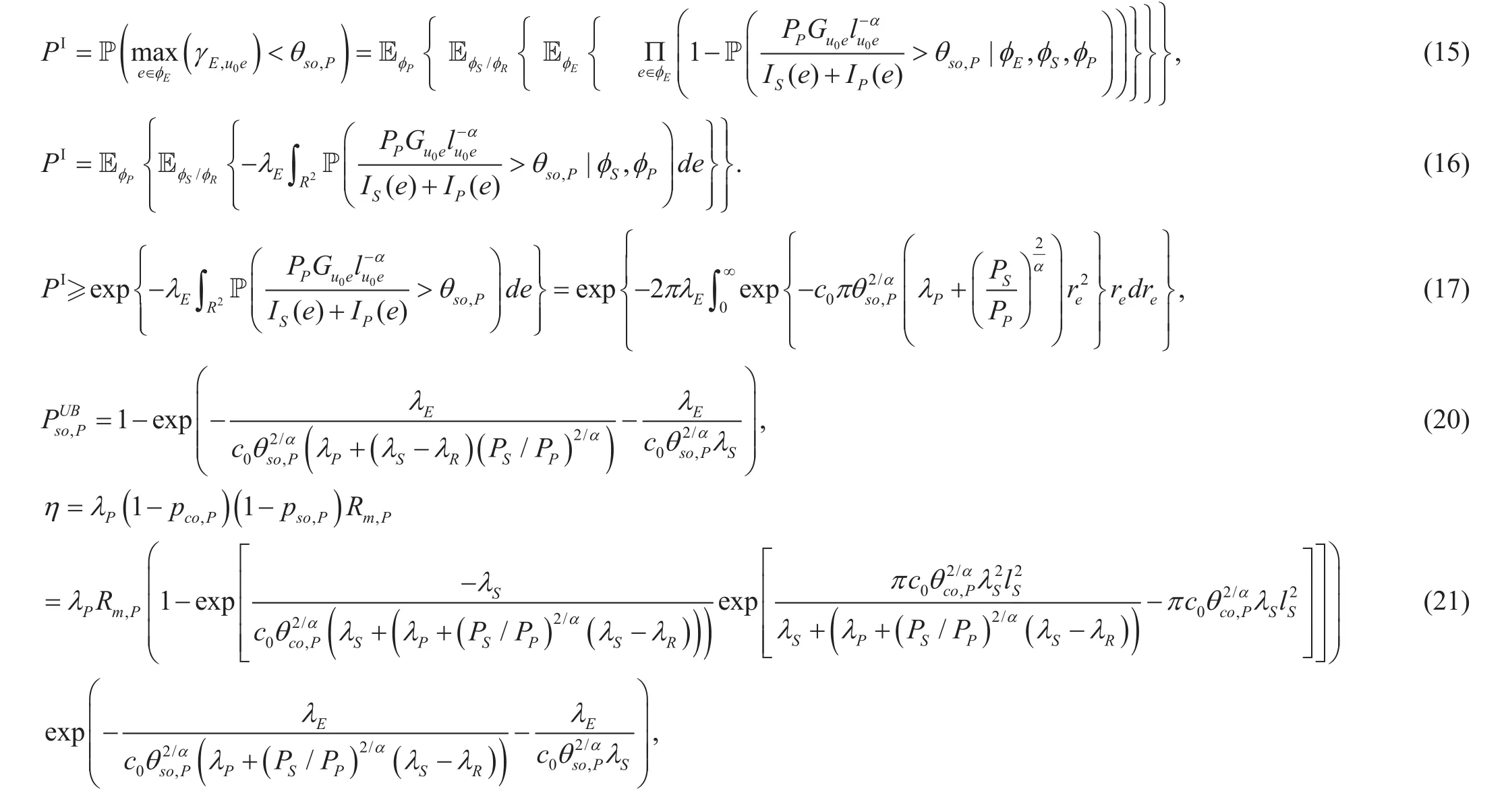
Thus, the practical power consumption of the cognitive relay networks including circuit and radio frequency chain power consumption,signal processing power, battery unit power consumption, etc. we consider a general power model given by
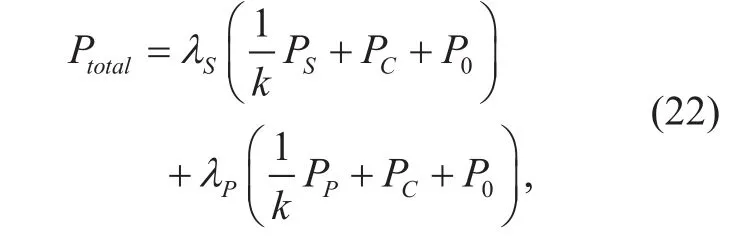
where k∈(0,1) denotes the power amplifier(PA) efficiency, PCdenotes the dynamic power consumption which includes the circuit power of corresponding radio frequency chains, P0accounts for the static power consumption which includes the baseband processing, battery unit power consumption, etc.
From (21) and (23), the relationship between the secure SE and the secure EE can be shown as ξ=η/Ptotal. It should be noted that maximizing the secure EE is different from maximizing the secure SE because not only the transmission power PSand potential intensity λSof relays should be designed carefully to maximize the secure SE, but also the total power consumption should be as small as possible. Therefore, it can be concluded that the transmission power PSand the potential density λSof relays affect the tradeoff between the secure SE and the secure EE of primary networks.
IV. JOINT SECURE SE AND EE MAXIMIZATION
Based on the analysis of secure SE and secure EE of the previous section, it is found that the transmission power PSand the potential density λSof relays affect the tradeoff between the secure SE and the secure EE. In this subsection, in order to jointly maximize the secure SE and EE simultaneously, we first turn the multi-objective optimization problem into a single-objective optimization problem by a tradeoff factor. Then an iterative algorithm is given to get the optimal transmission powerand the optimal potential relay density
4.1 Problem formulation
In order to optimize the secure SE and EE performance jointly, a multiple-objective function is established as shown below, which is a function of η(PS,λS), ξ(PS,λS).
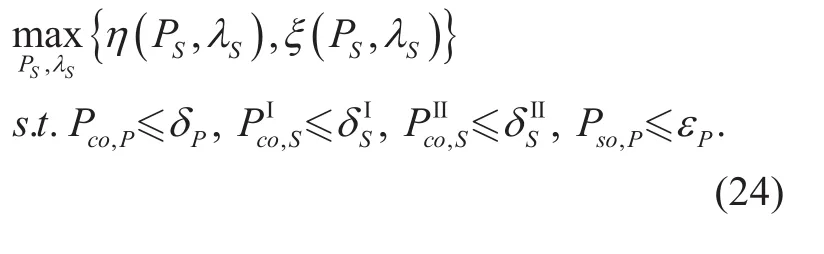
where δPis the reliability requirement of the primary network,andare the reliability requirement of the secondary network in the first phase and second phase, respectively.εPis the security requirement of the primary network.
To solve this multiple-objective problem,this paper adopts a popular approach just like[17, 19]: Turning the multi-objective optimi-zation problem into a single-objective optimization problem by a secure SE and EE tradeoff factor. The utility function is given by

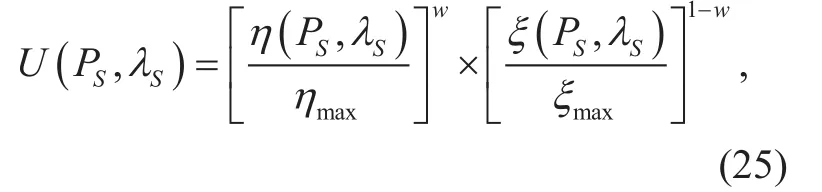
where w∈[0,1] is the preference for secure SE while 1−w is the preference for secure EE, ηmaxand ξmaxare the maximum achievable of the secure SE and EE, respectively.From (25), it is found that the normalized secure SE is non-decreasing with the preference w while the normalized secure EE is non-increasing with the preference w.
Further, the joint secure SE and EE optimization problem can be given as
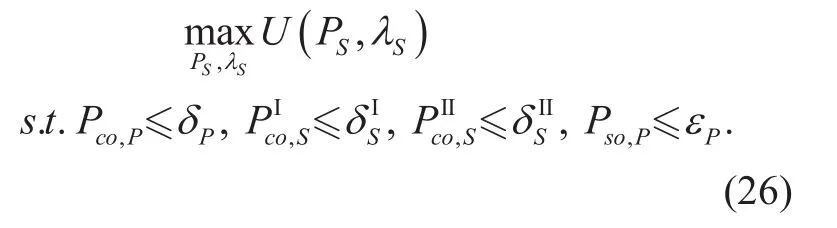
Since the optimization problem is a non-convex fraction programming problem,it is mathematically intractable to find the optimal solution. Thus, we give an iterative algorithm to get the optimal transmission powerand intensityof relays.
4.2 The iterative algorithm
The proposed algorithm is summarized in Algorithm 1, M is the maximum number of iterations, δ is the maximum tolerance. We first initialize the transmission power and potential intensity of relays. Then, we try to find the optimal intensity λS[m] with PS[m −1]. We analytically calculate the first-order derivative of U(PS,λS) with respect to λSfor a given PS. We numerically find thatis first positive and then negative. Consequently, U(PS,λS) is strictly quasi-concave with λSfor a given PS[28], it is easy to find the optimal intensity λS[m] with PS[m−1]using the binary search method. The similar property can be obtained on PSin the same way thus, the optimal transmission power PS[m] can be easily found based on λS[m].From the COP in (7-9) and SOP in (20), we can get the lower and upper bound of PSand λSwhich satisfy the reliability and security constraints. Thus, U(PS,λS) will not increase indefinitely due to the constraints of PSand λS. The loop will terminate once the algorithm converges sufficiently close to the optimal U(PS,λS) (i.e., when the conditionis satisfied) or the number of iterations exceeds a prescribed value M.
It should be noted that the proposed iterative algorithm is a suboptimal algorithm because of the iterative procedure for updating their respective solutions. Consequently, the optimal value of the transmission power and the potential relay intensity that maximizes U(PS,Sλ)may be a local optimum rather than global optimal due to the fact that the initial point PS[0]or λS[0] is selected randomly.
V. NUMERICAL RESULTS
Numerical results illustrating the proposed theoretical framework are presented in this section. We first present the impacts of the transmission power PSand potential relay density λSon the secure SE and EE tradeoff of the primary link. Then, we show how the weight factor w affects the secure SE and EE tradeoff. Furthermore, we compare the performances of our proposed optimal scheduling scheme with the random scheduling scheme to show the performance improvement. Finally, we compare different relay selection policies in improving secure SE and EE tradeoff. The system parameters are assumedas: PP=30 dBm, λP=5×10−4nodes/m2,nodes/m2,lP=10 m, lS=10 m,PC=10 dBm, P0=10 dBm, k=0.35, α=4,Rt,P=2 bits/sec/Hz, Rm,P=2 bits/sec/Hz.

Algorithm 1 Proposed iterative power and potential relay intensity optimal algorithm
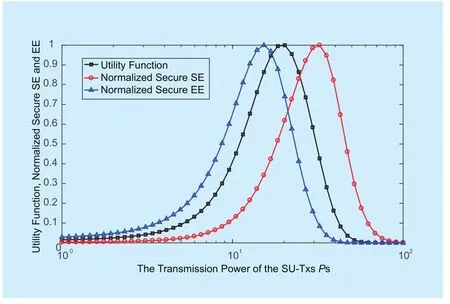
Fig. 2 Utility function, normalized secure SE and EE versus the relay transmission power PS
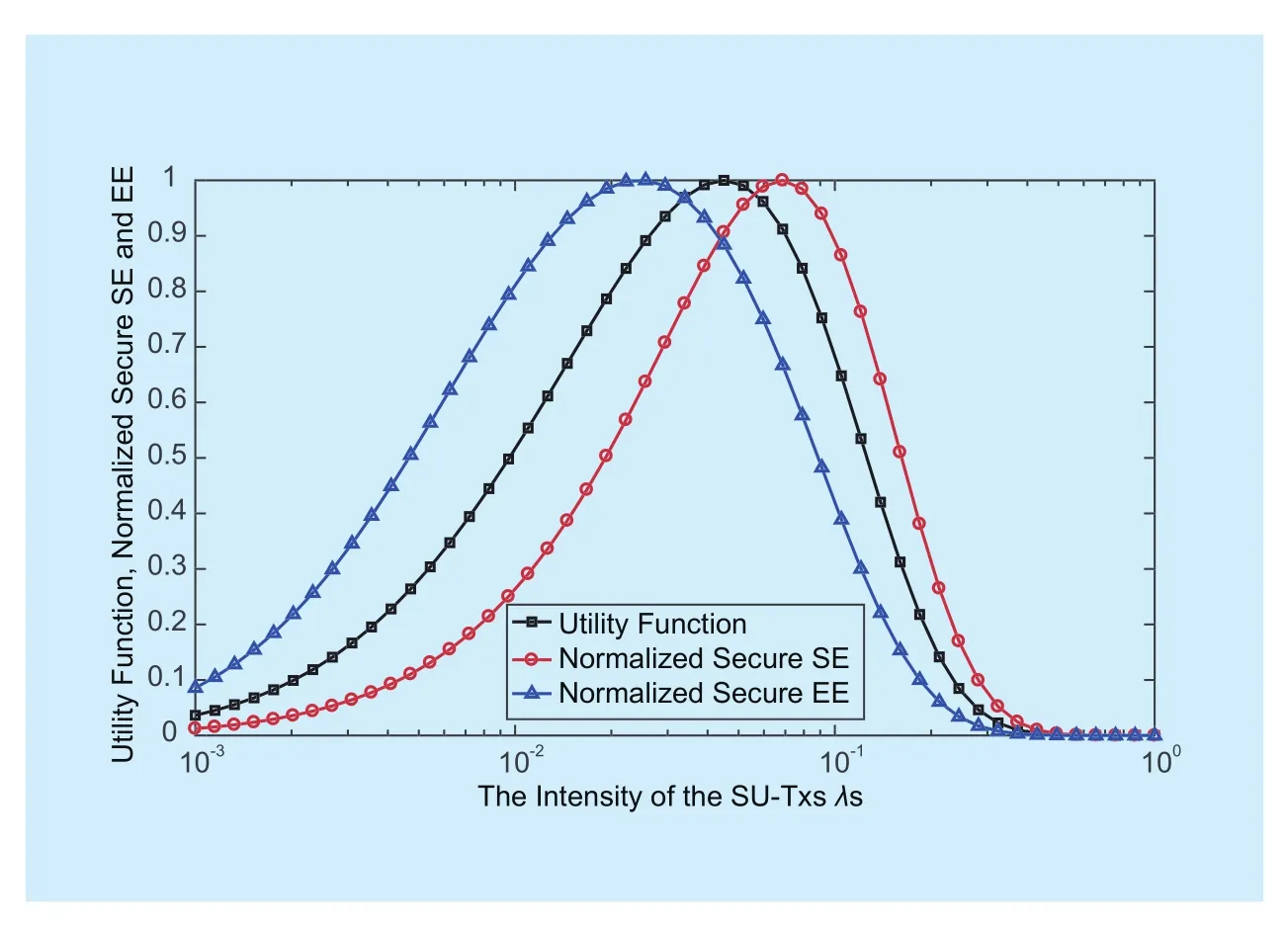
Fig. 3 Utility function, normalized secure SE and EE versus the potential relay intensity λS
First, we present the impacts of the transmission power PSand potential density λSof relays on the secure SE and EE tradeoff of the primary link in which w is fixed at 0.5.As shown in figure 2, both of the normalized secure SE and the normalized secure EE increase first then decrease with the increase of PS, but the transmission power PSis different when the normalized secure SE and normalized secure EE reach their optimal time which is coincides with the previous analytical results. Furthermore, the optimal PSfor maximizing the secure EE is less than the optimal PSfor maximizing the secure SE, due to the fact that the secure EE comprehensively considers the overall power consumption on the basis of considering the security and reliability of the primary link while the secure SE only consider the security and reliability. The impacts of potential relay density λSon the utility function, normalized secure SE and EE is shown in figure 3. Since the analysis of λSis very similar with PS, which is omitted here.
Then, we present the impacts of the secure SE weight factor w on the secure SE and EE tradeoff of the primary link. As shown in figure 4, the normalized secure EE is non-increasing while the normalized secure SE is non-decreasing with w which indicates that secure EE and secure SE are conflict with each other. It should be noted that the normalized secure SE and secure EE remain unchanged when w is close to 1, this is because PSoptand λSoptwill stay to constants when w is close to 1 due to the upper bounds on PSand λS. Clearly, the secure SE-EE tradeoff, determined by the difference between the secure SE and EE,is highest when w=0 and w=1. Furthermore, the three curves do intersect at a unique point, which can be clarified by the definition of U(PS,Sλ).
Furthermore, the secure SE-EE relationship under the proposed optimal scheduling scheme and random scheduling scheme is given in figure 5. The random scheduling scheme is the case where the transmission power and the intensity of relays are selected randomly.Obviously, outside the provided optimal solution set (marked with solid line), there does not exist another solution that improve at least one objective (secure SE or secure EE) without detriment to another one, which verified the effectiveness of the optimal scheduling scheme.
Finally, comparisons of the ORS policy and other reference policies in terms of normalized secure SE and normalized secure EE are plotted in figure 6. The first reference policy,denoted as random relay selection, is the case where PU-Txs select relay randomly from SU-Txs which can decode the information from PU-Tx correctly. The second reference policy, denoted as conventional direct transmission, is the case PU-Txs communicate with PU-Rxs directly without the help of relay. As shown in the figure 6, the ORS policy outperforms the other two policies since the reliability gain of ORS is greater than the loss of security when faced with small security threat such as λE=1e −4 nodes/m2. When the security threat becomes more severe such as λE=1e −3 nodes/m2, the performances of the three policies are getting worse than before. It should be note that the conventional direct transmission outperforms ORS in this case due to the fact the reliability gain of ORS is less than the loss of security. Accordingly, in order to further improve the secure SE and EE tradeoff, we should adaptively select different policies according to the eavesdropper environment.
VI. CONCLUSION
This paper studies the secure SE and EE tradeoff of cognitive relay networks where the locations of primary, secondary and eavesdropper nodes are modeled as independent HPPP. We found that both of relay transmission power and potential relay density arouse a tradeoff between secure SE and secure EE.By applying a unified SE-EE tradeoff metric,the secure SE and EE tradeoff problem is formulated as joint secure SE and EE maximization problem with a tradeoff factor. An iterative algorithm is given to get the optimal relay transmission power and potential relay density. Numerical results show that the scheduling of relay transmission power and density can improve the secure SE and EE tradeoff. We also found that the opportunistic relay selection policy is always superior to random relay selection policy. Furthermore, the opportunistic relay selection policy outperforms the conventional direct transmission policy when faced with small security threat (i.e., for smaller eavesdropper density). It is suggest that we should adaptively select different policies based on the eavesdropper environment.
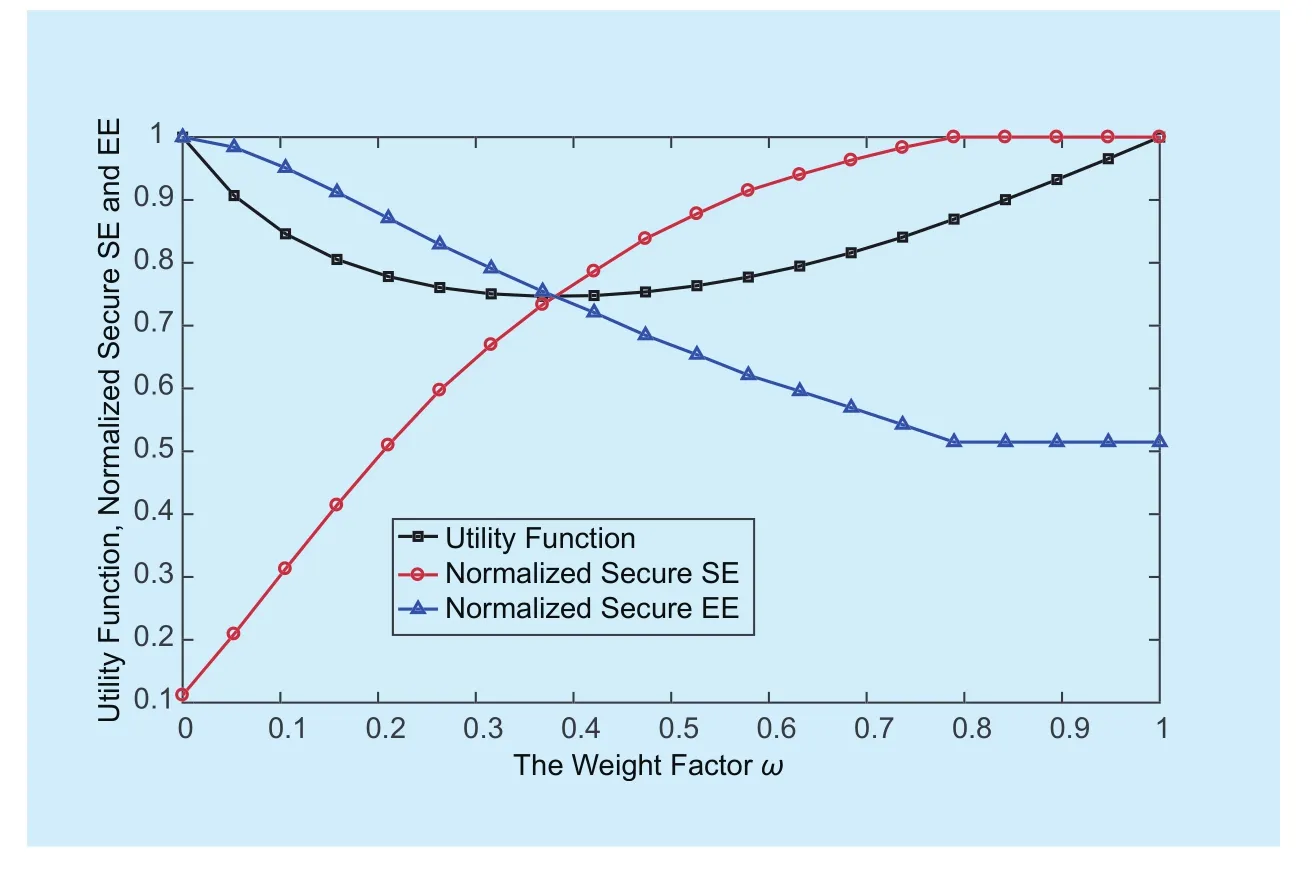
Fig. 4 Utility function, normalized secure SE and EE versus w
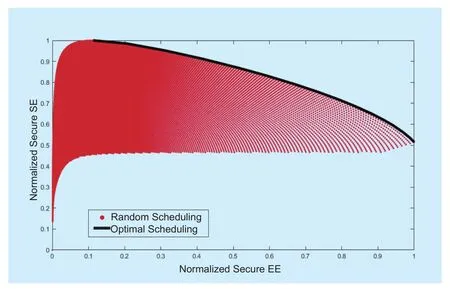
Fig. 5 Tradeoff between secure SE and EE under the proposed optimal scheduling scheme and the random scheduling scheme
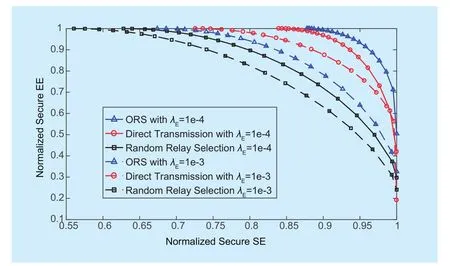
Fig. 6 Comparisons between the secure SE and EE of different policies
APPENDIX A
PROOF OF PROPOSITION 1
After selecting the best relay set from SU-Txs,the remaining SU-Txs aren’t HPPP anymore,since λSis much larger than λR, the distribution of the remaining SU-Txs follows a HPPP with spatial density λS−λR(λP) approximately.
We assume that the distance between relay rjand u0is x, the decoded probability of relay rjiswherecan be got from (1). Pjis further expressed as (27) shown in the bottom at this page.
Thus, the decoded probability of relay rjis given by
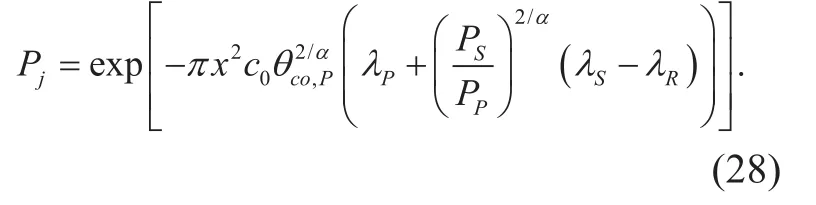
Define σ as the area of the circle centered at PU-Tx u0with radius x, and dσ as infinitely small ring with inner and outer diameters of x and x+dx, respectively. Thus, the average number of relays in dσ that can decode the data correctly is λRPjdσ. According to Prekopa’s theorem [31], the distribution of ωu0follows an inhomogeneous PPP. For a closed area A⊂R2, the average number of relays decoding data correctly from u0is
APPENDIX B
PROOF OF PROPOSITION 2
Based on the generating functional of the PPP ωu0, (6) can be expressed as (29) shown in the bottom at this page.
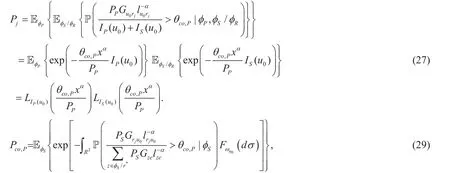
where

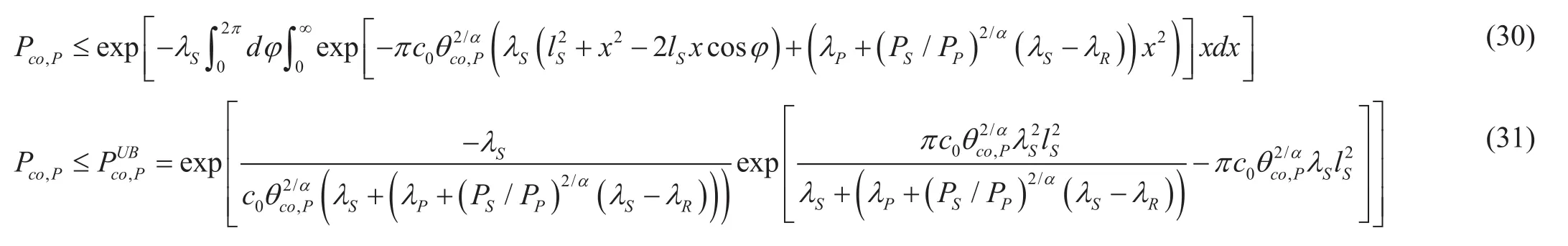
Applying Jensen’s inequality, an upper bound of Pco,Pis given by (30) at the top of this page.
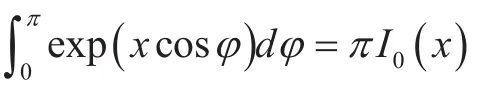
[1] A. N, 5G white paper. Next generation mobile networks, white paper, 2015.
[2] X. Li, T. Jiang, S. Cui, J. An, and Q. Zhang, “Cooperative communi- cations based on rateless network coding in distributed mimo systems,”IEEE Wireless Commun, vol. 17, no. 3, pp. 60–67, Jun. 2010.
[3] J. Mitola and G. Q. Maguire, “Cognitive radio:making software radios more personal,” IEEE pers. commun, vol. 6, no. 4, pp. 13–18, Aug.1999.
[4] L. Fan, S. Zhang, T. Q. Duong, and G. K. Karagiannidis, “Secure switch and stay combining SSSC for cognitive relay networks,” IEEE Trans.Commun, vol. 64, no. 1, pp. 70–82, Nov. 2016.
[5] X. Xu, W. Yang, and Y. Cai, “Opportunistic relay selection improves reliability-reliability tradeoffand security-reliability tradeoff in random cognitive radio networks,” IET Commun, vol. 11, no.3, pp. 335–343, Feb. 2017.
[6] J. Zhu, D. W. K. Ng, N. Wang, R. Schober, and V. K. Bhargava, “Analysis and design of secure massive MIMO systems in the presence of hardware impairments,” IEEE Trans. Wireless Commun., vol. 16, no. 3, pp. 2001–2016, Mar.2017.
[7] X. Zhang, M. R. McKay, X. Zhou, and R. W.Heath, “Artificial-noise- aided secure multi-antenna transmission with limited feedback,” IEEE Trans. Wireless Commun., vol. 14, no. 5, pp.2742–2754, May. 2015.
[8] H. Wang and T. Zheng, “Physical layer security in random cellular networks,” Springerbriefs in Computer Science, 2016.
[9] J. Zhu, R. Schober, and V. K. Bhargava, “Linear precoding of data and artificial noise in secure massive MIMO systems,” IEEE Trans. Wireless Commun., vol. 15, no. 3, pp. 2245–2261, Mar.2016.
[10] N. Yang, L. Wang, and G. Geraci, “Safeguarding 5G wireless commu- nication networks using physical layer security,” IEEE Commun. Mag., vol.53, no. 4, pp. 20–27, Apr. 2015.
[11] J. Hu, Y. Cai, N. Yang, X. Zhou, and W. Yang,“Artificial-noise- aided secure transmission scheme with limited training and feedback overhead,” IEEE Trans. Wireless Commun., vol.16, no. 1, pp. 193–205, Jan. 2017.
[12] R. Zhao, Y. Yuan, L. Fan, and Y. He, “Secrecy performance analysis of cognitive decode-and-forward relay networks in Nakagami-m fading channels,” IEEE Trans. Commun,vol. 65, no. 2, pp. 549–563, Feb. 2017.
[13] M. R. Abedi, N. Mokari, M. R. Javan, and H.Yanikomeroglu, “Limited rate feedback scheme for resource allocation in secure relay-assisted OFDMA networks,” IEEE Trans. Wireless Commun., vol. 15, no. 4, pp. 2604–2618, Apr. 2016.
[14] Z. Zhou, M. Dong, K. Ota, and Z. Chang, “Energy-efficient context- aware matching for resource allocation in ultra-dense small cells,”IEEE Access, vol. 3, pp. 1849–1860, 2015.
[15] Y. Wang, C. Li, Y. Huang, D. Wang, T. Ban, and L.Yang, “Energy- efficient optimization for downlink massive MIMO FDD systems with transmit-side channel correlation,” IEEE Trans. Veh.Technol., vol. 65, no. 9, pp. 7228–7243, Sep.2016.
[16] J. Ouyang, W. P. Zhu, D. Massicotte, and M. Lin,“Energy efficient optimization for physical layer security in cognitive relay networks,” 2016 IEEE ICC, pp. 1–6, May. 2016.
[17] W. Zhang, C. Wang, D. Chen, and H. Xiong,“Energy-spectral efficiency tradeoff in cognitive radio networks,” IEEE Trans. Veh. Technol., vol.65, no. 4, pp. 2208–2218, Apr. 2016.
[18] J. B. Rao and A. O. Fapojuwo, “An analytical framework for evaluating spectrum/energy efficiency of heterogeneous cellular networks,”IEEE Trans. Veh. Technol., vol. 65, no. 5, pp.3568–3584, May. 2016.
[19] D. Tsilimantos, J. M. Gorce, K. Jaffrs-Runser,and H. V. Poor, “Spectral and energy efficiency trade-offs in cellular networks,” IEEE Trans.Wireless Commun., vol. 15, no. 1, pp. 54–66,Jan. 2016.
[20] X. Xu, W. Yang, Y. Cai, and S. Jin, “On the secure spectral-energy efficiency tradeoff in random cognitive radio networks,” IEEE J. Sel. Areas Commun., vol. 34, no. 10, pp. 2706–2722, Oct.2016.
[21] H. Wang, T. Zheng, J. Yuan, D. Towsley, and M.H. Lee, “Physical layer security in heterogeneous cellular networks,” IEEE Trans. Commun., vol.64, no. 3, pp. 1204–1219, Mar. 2016.
[22] R. W. Heath, M. Kountouris, and T. Bai, “Modeling heterogeneous network interference using Poisson point processes,” IEEE Trans. Signal Process, vol. 61, no. 16, pp. 4114–4126, Aug. 2013.
[23] C. Ma, J. Liu, X. Tian, H. Yu, Y. Cui, and X. Wang,“Interference exploitation in D2D-enabled cellular networks: A secrecy perspective,” IEEE Trans. Commun., vol. 63, no. 1, pp. 229–242, Jan.2015.
[24] N. Yang, S. Yan, J. Yuan, R. Malaney, R. Subramanian, and I. Land, “Artificial noise: Transmission optimization in multi-input single-output wiretap channels,” IEEE Trans. Commun., vol. 63, no.5, pp. 1771–1783, May. 2015.
[25] J. Xu and L. Qiu, “Energy efficiency optimization for MIMO broadcast channels,” IEEE Trans.Wireless Commun., vol. 12, no. 2, pp. 690–701,Feb. 2013.
[26] F. Baccelli and B. B. laszczyszyn, Stochastic Geometry and Wireless Networks, Volume I: Theory, 1st ed. Hanover, MA: Now Publishers Inc.,2009.
[27] D. Stoyan, W. Kendall, and J. Mecke, Stochastic Geometry and Its Applications, 2nd ed. John Wiley and Sons, 1996.
[28] S. Boyd and L. Vandenberghe, Convex Optimization, 2004.
[29] I. S. Gradshteyn and I. M. Ryzhik, Table of integrals, series and products, 7th ed., 2007.
- China Communications的其它文章
- Design and Implementation of a TDD-Based 128-Antenna Massive MIMO Prototype System
- Symbol Error Rate Performance Analysis of Non-Orthogonal Multiple Access for Visible Light Communications
- On Uplink Non-Orthogonal Multiple Access for 5G:Opportunities and Challenges
- Radio Access Network Slicing Based on C/U Plane Separation
- Contract-Based Content Delivery in 5G Converged Networks
- Clustering of Virtual Network Function Instances Oriented to Compatibility in 5G Network

