基于天气预报的参考作物蒸发蒸腾量预测模型

余江斌，林剑辉*，高大帅

（北京林业大学工学院，北京 100083）

基于天气预报的参考作物蒸发蒸腾量预测模型

余江斌1，林剑辉1*，高大帅1

（北京林业大学工学院，北京 100083）

参考作物蒸发蒸腾量（ET0）是计算作物需水量和进行灌溉预报的基本要素。本文利用天气预报可测因子和Penman Monteith (PM)公式ET0计算值作为基础数据，分别建立BP神经网络模型和ANFIS自适应模糊神经推理系统模型，两种模型的估算值与PM公式的计算值没有明显差异，均表现出显著的相关性以及整体吻合度。本文对两种模型取相同的数据样本进行比较，BP-ET0预测结果的MRE值为32.13%，RMSE为0.134 mm,而R2达到了0.971，说明模型预测精度高，稳定性良好。相较于ANFIS-ET0的检验结果，BP-ET0模型的均方根误差更小（0.134 mm/d 〈 0.188 mm/d），表明其预测精度更高；而ANFIS-ET0模型估算值的平均相对误差明显小于BP-ET0模型估算值（16.92%〈32.13%），显示出ANFIS-ET0模型更高的稳定性。两种预测模型的输入项完全可以从当前短期天气预报因子中取得而不需要专用测量设备，程序操作简单，具有实用价值，为实时灌溉预报提供了理论基础。

参考作物蒸发蒸腾量（ET0）；BP神经网络；自适应模糊神经推理系统（ANFIS）；天气预报因子；灌溉实时预报；Penman Monteith

灌溉实时预报是灌溉实时调度的核心理论技术之一，参考作物蒸发蒸腾量（ET0）预测精度的高低直接影响灌溉实时预报的准确度，是计算作物需水量和进行灌溉管理的主要依据[1]。目前，逐日ET0的计算模型主要是采用FAO推荐的Penman Monteith (PM)公式，它是现今确定和计算逐日ET0比较精确且应用最多的方法[2-4]。但PM公式计算时需要很多气象数据，包括最高气温、最低气温、相对湿度、辐射（或日照时数）和风速等，应用时受到一定程度的限制[1]。因此，李彦等[5]应用多元线性回归法建立预测模型，运用日平均气温、日照时数、风速和相对湿度来预测ET0，虽然能够达到较高的预测精度，但是气象数据的获取还是相对繁琐，不具有实用性。在此基础上，国外学者Reynolds等[6]考虑到ET0的计算模型都是基于历史时间序列分析，根据历史ET0变化过程预测未来的ET0，认为采用数值天气预报数据（气温，相对湿度等）来进行ET0预报或估算正成为一种趋势，并且能达到更高的预测精度。其中Black等[7]使用这一思路在ET0的预测上做了相关研究，结果表明，根据数值天气预报数据进行ET0的估算具有高精度和低数据维度的优点，表现出很高的可行性。上述已有研究中，采用数值天气预报数据进行ET0的估算已经很常见[8-11]，但是结合天气预报信息（天气状况和风力状况等）进行ET0预报并不多见，相关研究表明天气预报信息对ET0的估算精度有一定的影响[12-14]。因此，本研究以天气预报可测因子为基础，可测因子包括天气状况、最高、最低气温和风力状况等[15]，建立BP神经网络模型和自适应模糊神经推理系统模型（ANFIS）估算逐日ET0，对两种模型的预测结果进行分析，为逐日ET0实时预报寻求捷径和提高预报精度，同时为有效优质的实时灌溉预报提供依据。

1 材料与方法

1.1 数据资料

试区在中国农业大学石羊河流域试验站，试验站位于甘肃省武威市（102°50'E，37°52'N），海拔1 580 m，气候类型为温带大陆性气候，年平均气温为7.8 ℃；四季降水较少，年降水量为60-610 mm。本研究以武威市1997年至1998年的天气预报可测因子和ET0公式计算值作为输入输出量进行BP神经网络的模型训练，并用1999年的相应数据进行模型检验；另一方面，本研究以2014年11月至2015年5月的天气预报可测因子和ET0公式计算值作为输入输出量进行ANFIS模型训练，逐月选择3 d相应数据进行ANFIS模型检验，并以此数据进行两种模型的对比研究，本文ET0的计算值均是通过FAO Penman-Monteith (PM)公式计算得出。

1.2 BP神经网络模型

BP神经网络是一种多层前馈神经网络，包括输入层、隐含层和输出层，相邻两层间单向链接，基本处理单元为非线性输入输出关系，一般使用Sigmoid函数或线性函数作为传递函数[16]。BP神经网络采用误差反向传播算法进行学习，在网络中数据从输入层经隐含层逐层向后传播，训练网络权值时，则沿着减少误差的方向，从输出层经过中间各层逐层向前修正网络的连接权值[16]。随着学习的不断进行，最终的误差越来越小[16]。基本结构见图1。

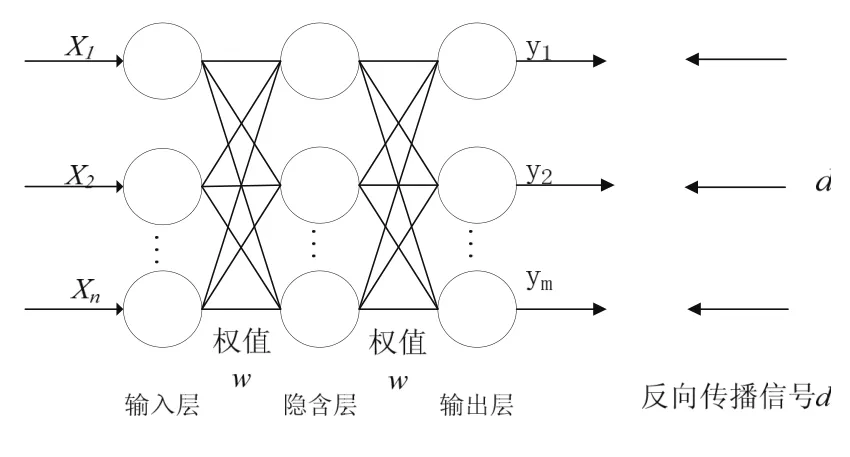
图1 BP神经网络结构Fig. 1 BP Neural network architecture

1.2.1 系统输入输出项选择 根据1997-1999年逐日气象因子（最高气温、最低气温、相对湿度、辐射（或日照时数）和风速）与ET0计算值的相关分析，发现日最高气温项（r =0.76）、太阳辐射项（日照时数，r =0.69）和风速（r =0.49）线性相关性相对较高，日常天气预报中的天气状况信息往往是由太阳辐射所决定，因此天气状况可以按照太阳辐射进行解析[16]，但由于获取的1997-1999年逐日天气预报数据缺少天气状况信息，所以选择日最高气温项和风速状况的量化指标即风力等级（通过对试验地区1997-1999年逐日风速的统计，整个统计周期最高风速等级只能达到4级，所以本文风力等级范围取0至4）作为模型的输入变量，输出项是ET0的值。风力状况量化指标见表1[12]。

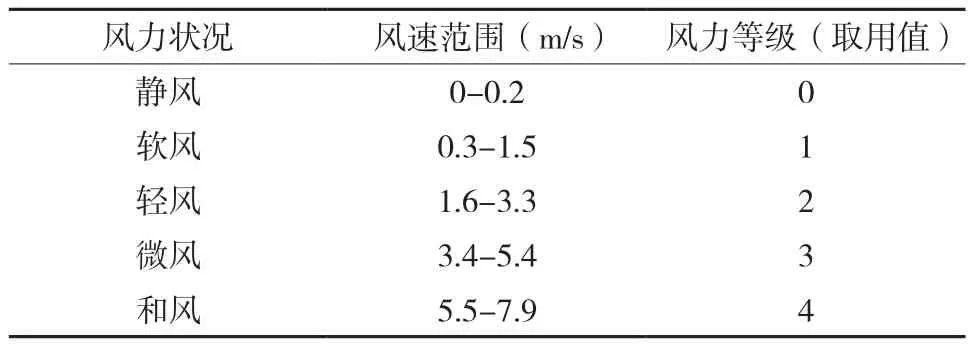
表1 风力状况量化指标Table 1 Quantitative indicators of wind conditions

1.2.2 系统构建 本文构建的BP-ET0模型为输入层、一个隐含层和输出层，共三层。隐含层的传递函数选择的是Tan-Sigmoid传输函数[16]（见公式1）；输出层选择的是线性函数，通过多次训练确定隐含层节点数为10，即网络模型的拓扑结构为2-10-1。

式中：n表示神经元节点对隐含层的输入，tansig(n)表示隐含层的输出。训练的参数设定为：最小学习速率为0.01，最大允许误差为0.001，最大迭代次数为1 000次。在满足目标精度要求或者达到最大迭代次数时，训练自动停止。1.3 自适应模糊神经推理系统（ANFIS）

自适应模糊推理算法是模糊逻辑与神经网络的结合物，既有模糊逻辑适于表示人的定性或模糊的经验和知识的特点，又有神经网络自适应、自学习机制[17]。实质是使用神经网络中的反向传播算法或者混合最小二乘估计的反向传播算法，对给定的一组输入/输出数据集进行学习来调整FIS(模糊推理系统)中变量的隶属度函数的形状参数[17]。图2是典型的一阶两输入/一输出ANFIS结构[17]。

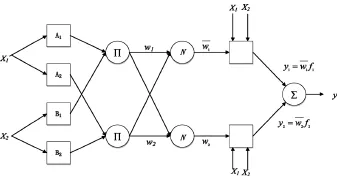
图 2 具有两个输入一个输出的ANFIS结构Fig. 2 ANFIS architecture for a two-input, two-rules first-order Sugeno model

1.3.1 系统输入输出项选择 由于1997至1999年获取的天气预报可测因子数据缺少天气状况信息，所以本文选择2014年11月至2015年5月的数据进行训练检验。根据数据集逐日气象因子（最高气温、最低气温、相对湿度、辐射（或日照时数）和风速）与ET0计算值的相关分析，发现类似于1.2.1节所述，日最高气温、太阳辐射以及风速线性相关性较高，而天气状况可以按照太阳辐射进行解析，所以选择日最高气温、风力状况以及天气状况作为模型的输入变量，输出项是ET0的值。

1.3.2 系统构建 根据常规天气预报，将天气状况分为晴、晴间多云、多云间阴、阴和雨（包括雨水等降水）5种情况。为了将一般语言与模糊推理结合起来，分别将这5种情况对应阿拉伯数字5-1，以便在模糊系统中进行模糊推理。风力状况根据表1给出的量化方法，同样分为5种情况对应阿拉伯数字0-4。最高气温项根据2014年11月至2015年5月逐日数据分析和整理，得到其基本特征和模糊设置。表2是输入项三变量模糊设置。

输入隶属度函数采用高斯（正态）分布函数，输出量隶属函数选择线性函数。高斯分布是统计中最为常用的函数，他在模糊逻辑中具有非常重要的地位。高斯（正态）分布函数的表达式为：

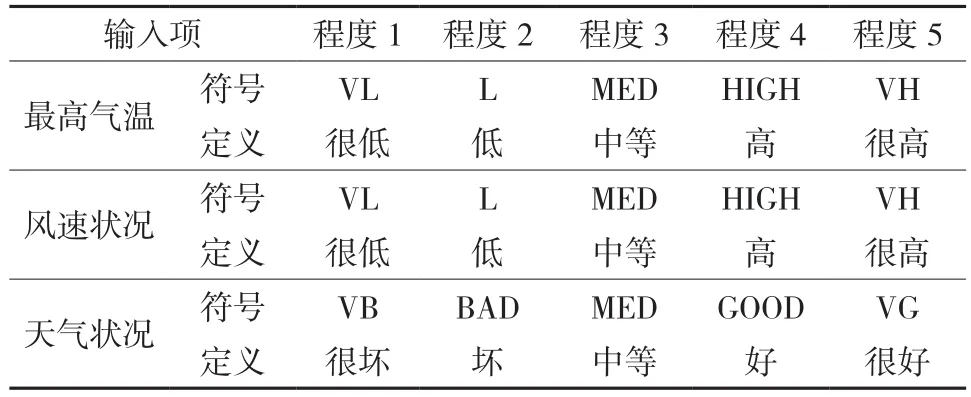
表 2 ET0-ANFIS推理系统输入项模糊设置Table 2 Fuzzy set of input items of ET0-ANFIS inference system

式中：c表示均值；σ表示方差；x表示隶属度函数的输入；y表示隶属度函数的输出。其中方差（σ）和均值（c)决定了高斯函数的形状：c决定了峰值点的位置，σ决定了函数曲线的舒展程度[17]。本文使用matlab模糊工具箱提供的图像化工具函数anfisedit[18]对ANFIS进行训练和检验，其中通过减法聚类的方法自动生成初始模糊推理系统，采用hybrid混合法训练，误差阈值设为0，训练周期为30。

2 结果与分析

本文的模型训练与检验结果均以平均相对误差(MRE)、均方根误差(RMSE)以及决定系数(R2)作为考察指标。其中平均相对误差反映模型的稳定性，误差越小，稳定性越好；均方根误差以及决定系数反映模型的预测精度[19]，均方根误差越小且决定系数越接近于1，表明该模型预测精度越高。

2.1 BP-ET0模型结果与分析

图3至图6分别是BP-ET0模型的训练结果与检验结果和使用PM公式计算结果的比较，其中图3是模型训练结果的ET0两年内变化曲线，图5是PM计算值与BP估算值的线性相关分析图。从模型训练结果的年内变化来看，ET0基本变化规律每年之间基本类似，即从1月到6月逐渐增大，6月为各月中的最大值，7月至12月逐渐减小；比较PM计算值与BP估算值年内变化差异，可以看出从5月至7月间和8月至9月间，两种计算方法的差异相对偏大，其中5-6月MRE为25.45%，8-9月MRE为30.12%；而12月至二月间，两种计算方法的结果比较接近，MRE为10.32%，从ET0的年内数据波动幅度来看，波动幅度较大的时期主要集中在4月到8月之间，这种大的起伏可能是年内气象因素阶段影响造成的。对于总体的训练结果而言，MRE为17.68%，RMSE为0.466 mm/d，而R2达到了0.919，说明模型训练结果的预测精度较高，稳定性好（见表3）。

图4和图6分别是模型检验结果的ET0变化曲线和线性相关图，从年内变化差异来看与训练结果基本类似，同样是5-7月和8-9月差异较大，MRE分别为24.12%和31.25%，而12月至2月PM计算值与BP估算值结果很接近，没有太大偏差，MRE为9.71%。数据起伏较大同样集中在4-8月。从检验数据的总体结果而言（表3），检验结果相关性相比训练结果稍小，但是仍然达到了较高的相关性，但MRE相比训练结果更小，说明通过BP模型训练之后其预测相对误差更小，结果更加可靠。总体而言，BP-ET0模型的预测效果较好，能够达到较高的预测精度以及稳定性。2.2 ANFIS-ET0模型结果与分析

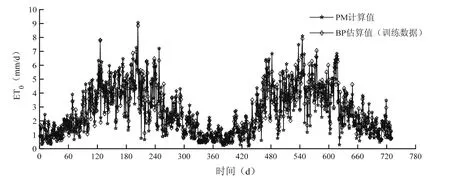
图3 1997-1998年内ET0变化过程Fig. 3 Change process of ET0during 1997-1998

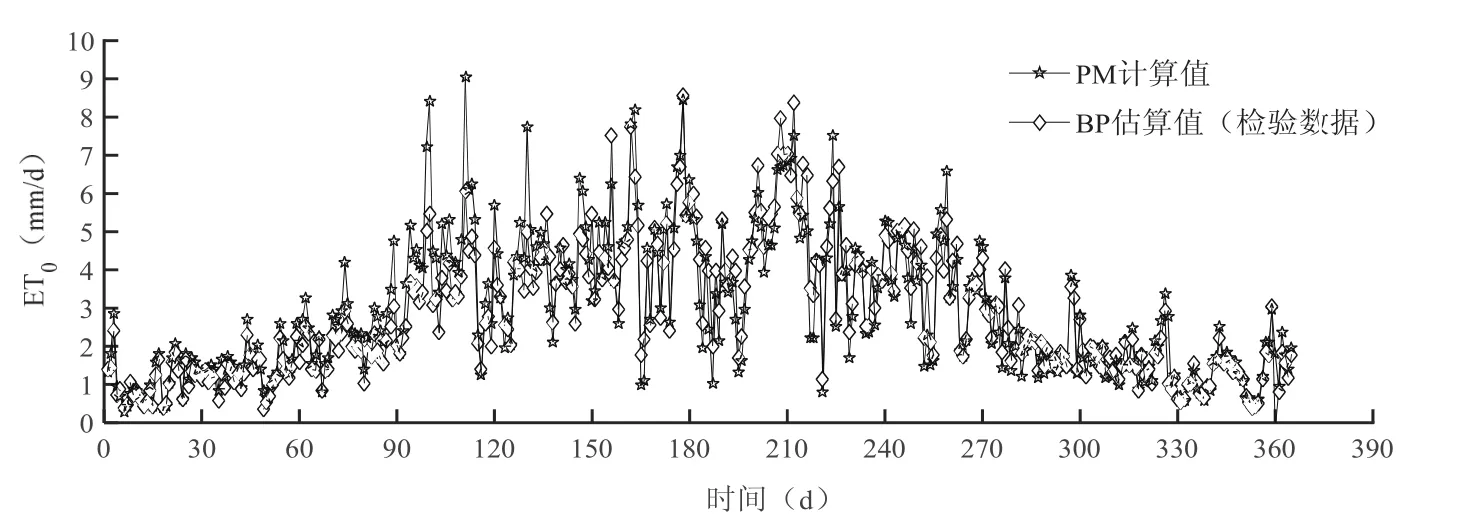
图4 1999年内ET0变化过程Fig. 4 Change process of ET0during 1999

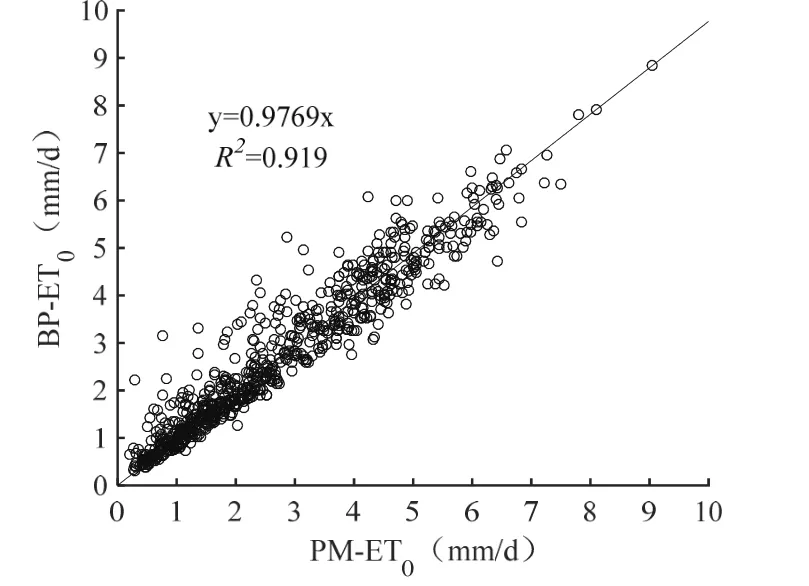
图5 PM与BP训练结果的相关分析Fig. 5 Correlation analysis between PM and BP training results

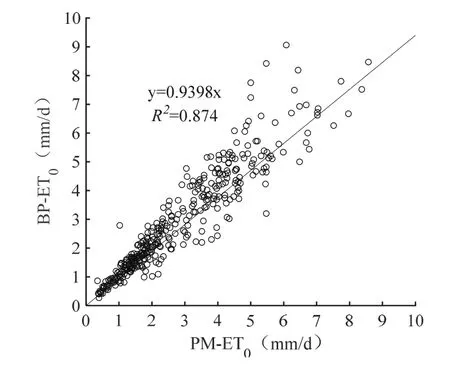
图6 PM与BP检验结果的相关分析Fig. 6 Correlation analysis between PM and BP testing results

表 3 BP-ET0模型训练与检验结果的统计参数Table 3 Statistic parameters of BP-ET0training and testing results

根据模型输入输出项的结果分析和相应专家知识，推理系统共产生5×5×5=125个模糊规则。通过训练之后模型定义的输入项日最高气温、天气状况以及风速状况的隶属度函数见图7，图中模糊设置（VB、BAD、MED、LOW等）具体含义见表2。

图8到图11分别是ANFIS-ET0模型训练与检验的数据结果分析图，图8和图9是ET0变化曲线，图10和图11是二者的线性相关分析图；其中训练数据选择的是2014年11月至2015年5月的ET0数据；检验数据取每个月10，20，30（二月取28日）日的ET0数据，共18个数据点。从训练结果的ET0变化曲线来看，11月至5月预测值与PM计算值都是在逐月增大；而从ET0的差异性变化来看，前四个月ET0的预测值与PM计算值误差较小，MRE为12.24%，后两个月的误差稍大，MRE为37.78%，而且3月至5月间，ET0的起伏较大。究其原因，本文认为由于ANFIS算法的模糊推理规则是以年为周期进行设计的，是认为年内无差异的，才会造成不同月份季度之间的差异。如果在此基础上针对地区差异，年内分阶段进行系统设计，可以减小这种误差。而对训练结果进行整体分析，其中MRE为24.20%，RMSE为0.277 mm/d，而R2达到了0.917（见表4），说明模型训练结果的预测精度高，稳定性好。对于检验结果，观察所选取的18个数据点，会发现第16个数据点预测值和PM计算值差异明显并且相比第15个数据点数值大小有大幅的跳跃，而这与训练结果的4月至5月相对误差较大、起伏明显的特点相吻合，说明验证结果与训练结果类似，整体的数据分析结果相比训练结果，相关性更高、相对误差更小（见表4）。总体而言，ANFIS-ET0模型的预测效果较好，能够达到较高的预测精度以及稳定性。

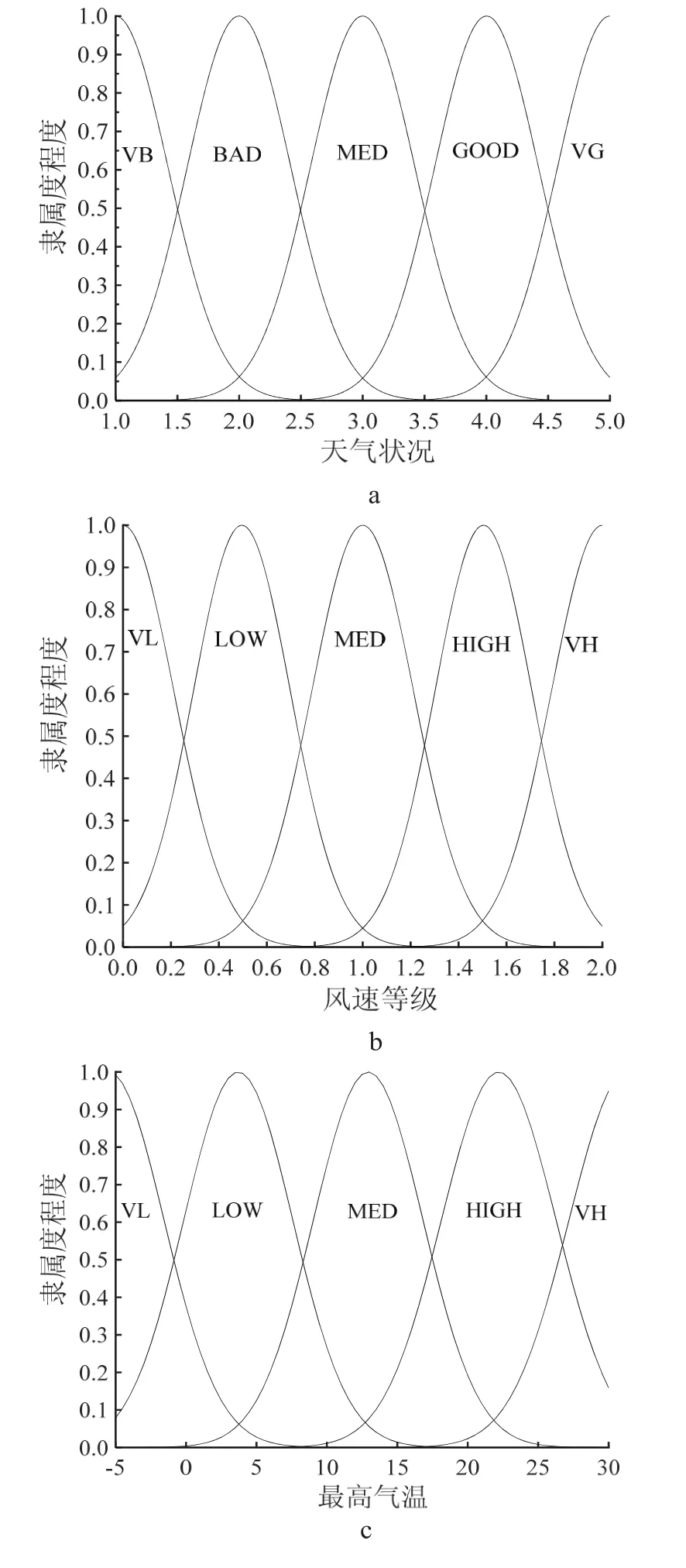
图7 训练后推理系统输入量的隶属度函数Fig.7 Membership functions defined after training for the input variables

表 4 ANFIS-ET0模型训练与检验结果的统计参数Table 4 Statistic parameters of ANFIS-ET0training and testing results

2.3 模型比较

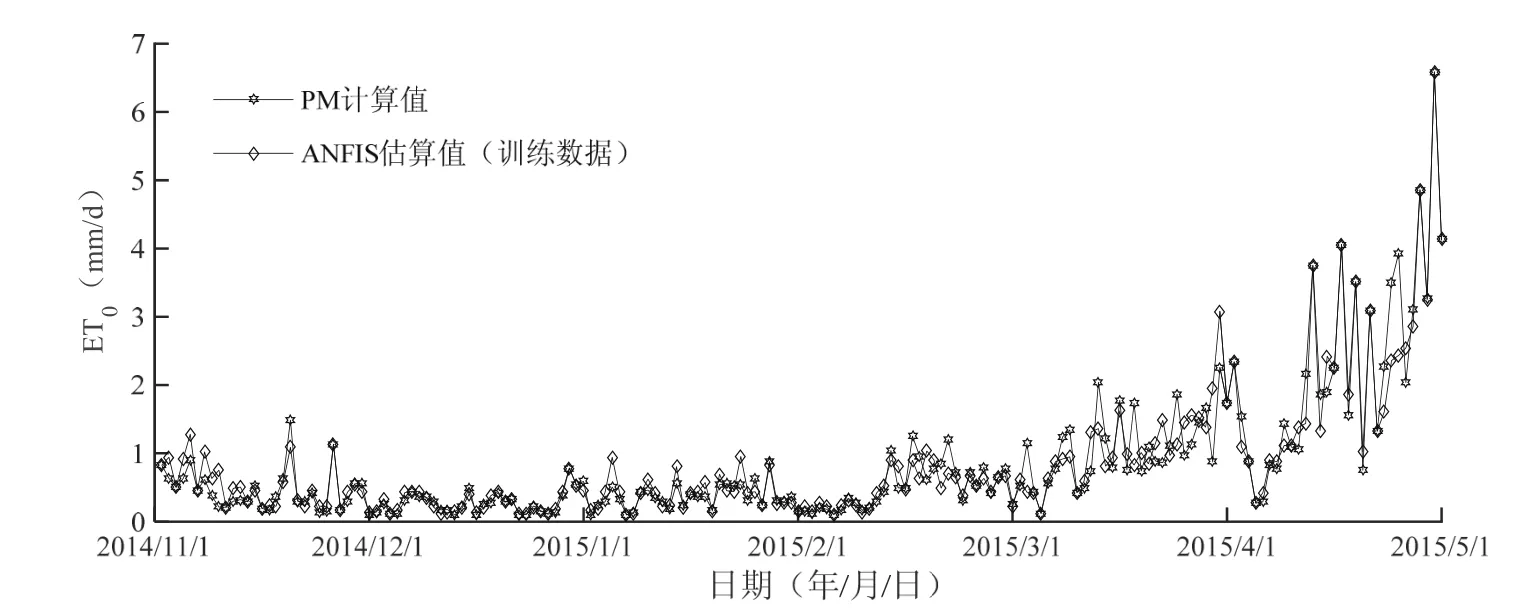
图8 2014/11至2015/5时段内的ET0变化过程Fig. 8 Change process of ET0 during 2014/11-2015/5

采用上述ANFIS-ET0模型的检验数据作为模型比较样本，将2014年11月至2015年5月逐月10、20以及30日（二月取28日）的风力状况以及日最高气温作为BP-ET0模型的输入量，ET0作为输出量，并将输出结果与ANFIS-ET0的检验结果进行比较，对PM-ET0计算值与两种模型的预测结果进行汇总对比，其中图12是三者的ET0变化曲线，图13是线性相关分析图。从图12可以看出三者的变化趋势基本类似，从ET0的值来看，总体BPET0的估算值要略大，BP-ET0预测结果的MRE值为32.13%，RMSE为0.134 mm,而R2达到了0.971，说明模型预测精度高，稳定性良好。相较于ANFISET0的检验结果（见表4），BP-ET0模型的均方根误差更小（0.134 mm/d〈0.188 mm/d），表明其预测精度更高；而ANFIS-ET0模型估算值的平均相对误差明显小于BP-ET0模型估算值（16.92% 〈 32.13%），显示出ANFIS-ET0模型更高的稳定性。

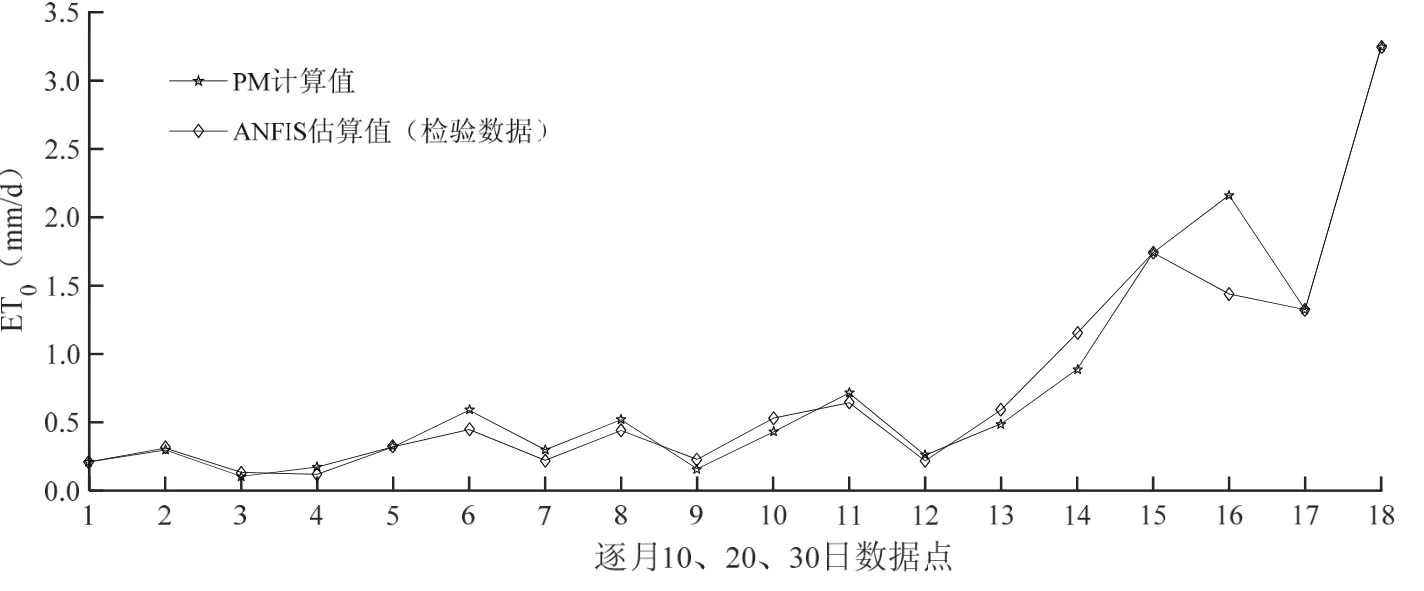
图9 逐月10、20、30日的ET0变化过程Fig. 9 Change process of ET0Monthly 10, 20, 30

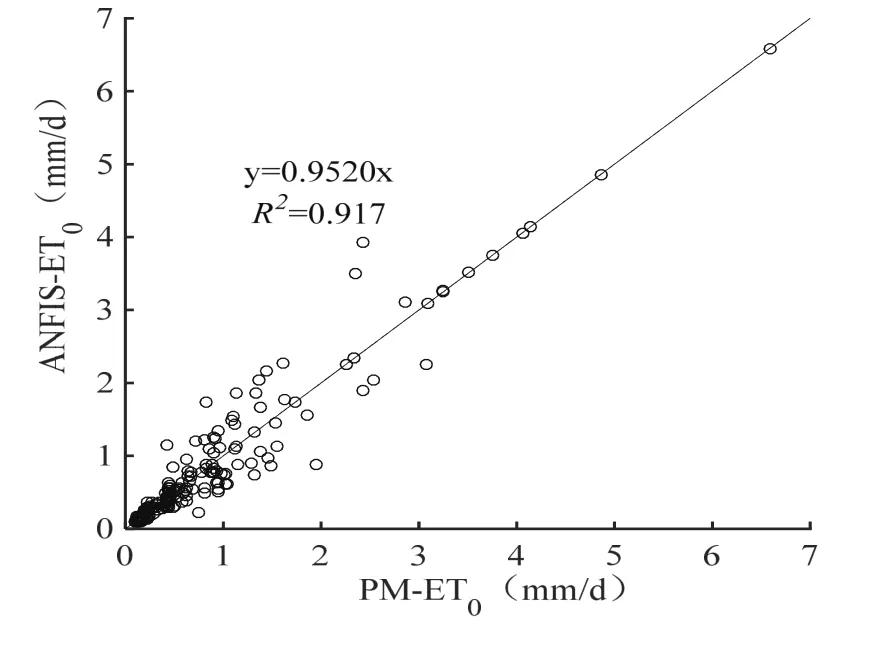
图10 PM与ANFIS训练结果的相关分析Fig. 10 Correlation analysis between PM and ANFIS training results

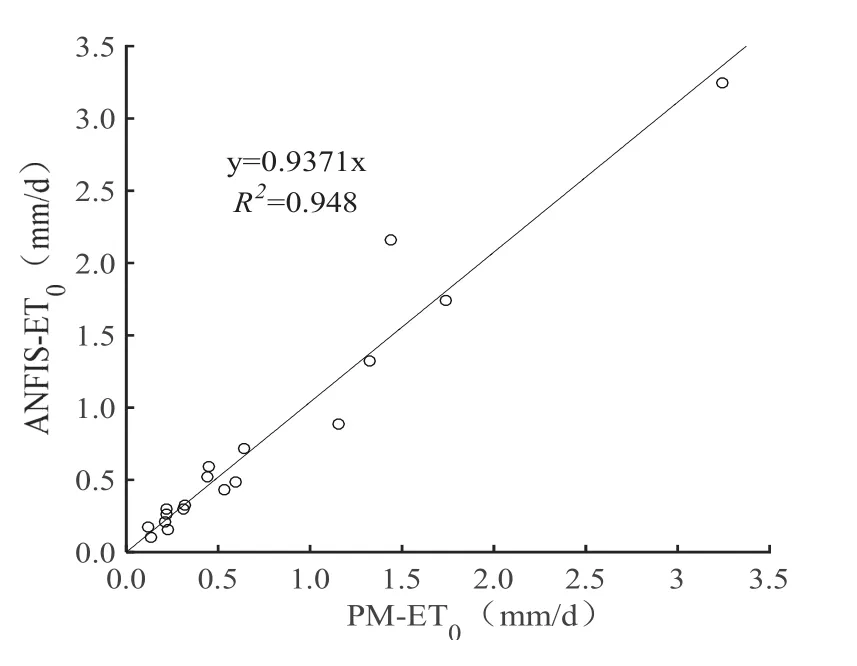
图11 PM与ANFIS检验结果的相关分析Fig. 11 Correlation analysis between PM and ANFIS testing results

3 讨论

针对本文提出的BP-ET0以及ANFIS-ET0模型，分别与前人建立的预测模型进行比较，均表现出类似的预测精度与稳定性。

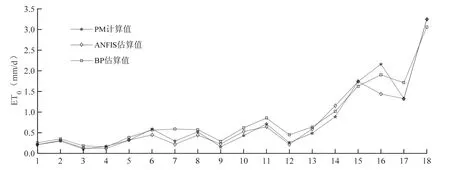
图12 ET0变化过程对比图Fig. 12 Comparison of ET0change process

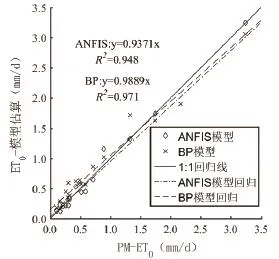
图13 模型相关性比较Fig. 13 Comparison of model correlation

将本文建立的BP-ET0模型与彭世彰等[20]建立的BP神经网络模型进行比较，针对训练样本，彭世彰等建立的模型训练结果中决定系数为0.966略高于本文的0.919，平均相对误差为11.2%低于本文的17.7%，但总体来说没有太大差异，检验样本也有类似的结果。并且本文的训练样本为两年的逐日气象数据，检验样本为一年的气象数据，在样本容量上相比彭世彰等[20]建立模型所用的一年训练样本，两个月的检验样本要更大，训练结果也更具可靠性；另一方面，彭世彰等[20]在建立模型时使用的模型输入维度比本文要大，增加了日序数这一输入变量，结果表明日序数在ET0预测模型中起到了一定的作用，后续研究可以借鉴将此气象因子考虑到模型当中。

本文建立的ANFIS-ET0模型与蔡甲冰等[17]建立的ANFIS模型进行比较，由于本文除了将天气状况和日最高气温作为模型输入，还在蔡甲冰等的基础上增加了风力状况这一重要变量，所以模型训练的结果要明显优于蔡甲冰等的训练模型。其中本文的决定系数为0.948，相关性高于蔡甲冰等建立的ANFIS模型(R2=0.699)[17]，平均相对误差也更小，表明本文建立的ANFIS-ET0模型具有更高的预测精度。

与前人建立的基于相同算法的模型比较，本文建立的模型均具有相当的预测精度。在此基础上，本文将建立的BP-ET0、ANFIS-ET0模型与李彦等[5]建立的多元线性回归模型进行比较：李彦等建立的多元线性回归模型是以日平均气温、日照时数、风速和相对湿度作为模型的输入，模型训练的结果中相关性分析为R2=0.937，低于本文所建立的模型；其模型检验结果中，PM计算值与预测值没有明显偏差，可能与检验数据集的数据点选择有关，误差相比本文更小，但其选取的模型输入因子都是很难从天气预报中获取的气象数据，因此其实用性相较本文略差，本文选取的输入因子都是天气预报基本参数，实用性更强。

在传统的模型拟合算法的基础上，也有部分学者应用了神经网络之后机器学习的新热点—支持向量机（SVM）来建立预测模型，张展羽等[12]建立了基于天气预报的LS-SVM预测模型，文中对天气预报可测因子作为模型输入的不同组合方式进行了比较与训练，最终建立了基于气温、天气类型和风速等级三个输入量的LS-SVM模型，输入量与本文选择的相同，但相关系数R2=0.965略低于本文建立的两种预测模型，均方根误差RMSE=0.518 mm也比本文误差更大；但其建立的SVM模型预测速度更快，降低了预测模型的复杂度，后续研究可以有所借鉴。

由于本研究所用模型的训练样本不同，对模型比较结果的可信度会有影响，所以下一步研究需要在模型样本上统一，提高模型的可靠性。

4 结论

本研究使用BP神经网络模型与ANFIS自适应模糊神经推理系统模型估算ET0，以天气预报可测因子作为模型的输入量，与PM公式相比虽然减少了输入因子，但模型的训练与检验结果表明，两种模型均能达到较低的预测误差并保证高相关性。通过对两种模型的对比，BP神经网络模型的预测精度相对更高，而从稳定性上而言，ANFIS模型的稳定性有明显的优势；通过与前人预测模型的比较,表明本文建立的预测模型具有一定的可靠性。

本研究结果表明：两种模型在根据天气预报可测因子预测ET0具有可行性，能达到较高的预测精度，对缺少气象站地区的实时灌溉预报方法提供了理论基础；该模型操作简单，所需气象参数少，相较于根据PM公式计算的获取方式，可以通过将模型移植到便携式设备上（如手机终端），从而投入实际农业灌溉预报的应用。

[1] 迟道才, 王晓渝, 张瑞, 等. 基于天气预报估算参考作物蒸发蒸腾量的预测模型比较[J]. 沈阳农业大学学报, 2008, 39(4): 455-458. Chi D C, Wang X Y, Zhang R, et al. Real-time ETo forecasting by synoptial report[J]. Journal of Shenyang Agricultural University, 2008, 39(4): 455-458.

[2] 顾世祥, 何大明. 逐日参照腾发量预测的改进方法[J]. 水利学报, 2005, 36(11): 1292-1297. Gu S X, He D M. Improved method for daily evapotranspiration prediction[J]. Journal of Hydraulic Engineering, 2005, 36(11): 1292-1297.

[3] 佟玲, 康绍忠. 区域作物耗水时空分布影响的研究进展[J]. 节水灌溉, 2004(1): 3-6. Tong L, Kang S Z. Advance in research on the impact of spatial and temporal distribution on regional crop evapotranspiration[J]. Water Saving Irrigation, 2004(1): 3-6.

[4] 胡顺军, 康绍忠. 阿拉尔灌区参考作物潜在腾发量的变化特征及相关性分析[J]. 灌溉排水学报, 2004, 23(6): 59-61. Hu S J, Kang S Z. Characteristics and dependence analysis reference crop evapotranspiration in Alaer irrigated area in Tarim River Basin[J]. Journal of Irrigation and Drainage, 2004, 23(6): 59-61.

[5] 李彦, 陈祖森, 张宝, 等. 参考作物蒸发蒸腾量的多元线性回归模型研究[J]. 新疆农业大学学报, 2005, 28(1): 70-72. Li Y, Chen Z S, Zhang B, et al. Study on the method of reference crop evapotranspiration by dependence analysis[J]. Journal of Xinjiang Agricultural University, 2005, 28(1): 70-72.

[6] Reynolds A G, Niu L X, Christiane D S. Use of electrical conductivity to assess irrigation impacts on grapevine winter hardiness[J]. International Journal of Fruit Science, 2014, 14(3): 267-283.

[7] Black T A, Gardner W R, Thurtell G W. The prediction of evaporation, drainage, and soil water storage for a bare soil[J]. Soil Science Society of American Journal, 1969, 33(5): 655-660.

[8] 霍再林, 史海滨, 陈亚新, 等.内蒙古地区ET0时空变化与相关分析[J]. 农业工程学报，2004, 20(6): 60-63. Huo Z L, Shi H B, Chen Y X, et al. Spatio-temporal variation and dependence analysis of ET0in north arid and cold region[J]. Transactions of the Chinese Society of Agricultural Engineering, 2004, 20(6): 60-63.

[9] 吴普华, 牛文全. 节水灌溉与自动化控制技术[M]. 北京: 化工工业出版社, 2002. Wu P H, Niu W Q. Water Saving Irrigation and Automatic Control Technology[M]. Beijing: Chemical Industry Press, 2002.

[10] 李远华, 罗金耀. 节水灌溉理论与技术[M]. 湖北: 武汉大学出版社, 2003. Li Y H, Luo J Y. Theory and Technology of Water Saving Irrigation[M]. Hubei: Wuhan University Press, 2003.

[11] 刘钰, Periera L S. 气象数据缺测条件下参照腾发量的计算方法[J].水利学报, 2001(3): 11-17. Liu Y, Periera L S. Calculation methods for reference evapotranspiration with limited weather data[J]. Journal of Hydraulic Engineering, 2001(3): 11-17.

[12] 张展宇, 王声峰, 段爱旺, 等. 基于天气预报的参考作物蒸发量的LS-SVM预测模型[J]. 水科学进展, 2010, 21(1): 63-68. Zhang Z Y, Wang S F, Duan A W, et al. Least squares support vector machines model for predicting reference evapotranspiration based on weather forecasts[J]. Advances in Water Science, 2010, 21(1): 63-68.

[13] 赵琪, 罗玉峰, 彭世彰, 等. 基于天气预报和Penman-Monteith公式的短期逐日参考作物蒸发量预报[J]. 节水灌溉, 2014(1):1-4. Zhao Q, Luo Y F, Peng S Z, et al. Short-term daily reference crop evapotranspiration forecast Based on weather forecast and Penman-Monteith Equation[J]. Water Saving Irrigation, 2014(1): 1-4.

[14] 霍再林, 史海滨, 李为萍, 等. 参考作物蒸发蒸腾量的人工神经网络模型研究[J]. 沈阳农业大学学报, 2004, 35(5/6): 436-438. Huo Z L, Shi H B, Li W P, et al. Artificial neural network model for reference evapotranspiration[J]. Journal of Shenyang Agricultural University, 2004, 35(5/6): 436-438.

[15] 段青春, 邱林. 基于混沌遗传程序设计的参考作物腾发量预测模型[J]. 水利学报, 2006, 37(4): 499-503. Duan Q C, Qiu L. Model for predicting reference evapotranspiration based on genetic programming with chaos algorithm[J]. Journal of Hydraulic Engineering, 2006, 37(4): 499-503.

[16] 刘丙军. 基于小波变换的BP神经网络参考作物腾发量预测模型[J]. 武汉大学学报, 2007, 40(1): 69-73. Liu B J. Reference crop evapotranspiration forecasting model for BP neural networks based on wavelet transform[J]. Engineering Journal of Wuhan University, 2007, 40(1): 69-73.

[17] 蔡甲冰, 刘钰, 雷廷武, 等. 根据天气预报估算参照蒸腾量的模糊神经网络方法[J]. 农业工程学报, 2005, 21(12): 108-111. Cai J B, Liu Y, Lei T W, et al. Daily reference evapotranspiration estimation from weather forecast messages-the ANFIS method[J]. Transactions of the Chinese Society of Agricultural Engineering, 2005, 21(12): 108-111.

[18] 闻新, 周露, 李东江, 等. MATLAB模糊逻辑工具箱的分析和应用[M]. 北京: 科学出版社, 2002. Wen X, Zhou L, Li D J, et al. Analysis and Application of MATLAB fuzzy logic toolbox[M]. Beijing, Science Press, 2002.

[19] 孟明, 牛东晓, 孟宁. 基于主成分分析的神经网络评价模型研究[J]. 华北电力大学学报, 2004, 31(2): 53-56. Meng M, Niu D X, Meng N. Neural network evaluation model based on principal component analysis[J]. Journal of North China Electric Power University, 2004, 31(2): 53-56.

[20] 彭世彰, 魏征, 徐俊增, 等. 参考作物蒸腾量主成分神经网络预测模型[J]. 农业工程学报, 2008, 24(9): 161-164. Peng S Z, Wei Z, Xu J Z, et al. Estimation model for reference evapotranspiration by neural network based on principal components[J]. Transactions of the Chinese Society of Agricultural Engineering, 2008, 24(9): 161-164.

（责任编辑：王育花）

Forecast model of reference crop evapotranspiration based on weather forecast

YU Jiang-bin1, LIN Jian-hui1, GAO Da-shuai1
（School of Technology, Beijing Forestry University, Beijing 100083, China）

Reference crop evapotranspiration (ET0) is a basic property to calculate crop water requirement and irrigation scheduling. The weather forecast measurable variables and ET0calculated by Penman Monteith (PM) formula were used as input to develop the BP neural network model and ANFIS adaptive neural fuzzy inference system model. The estimated value of the two models and the ET0calculated by the PM formula was not significantly different, showing signifcant correlation and overall degree of agreement. The two models were compared with the same data samples. The MRE value of BP-ET0prediction was 32.13%, RMSE was 0.134 mm, and R2was up to 0.971, which shows that the model has high prediction accuracy and good stability. Compared with the ANFIS-ET0test results, the root mean square error of BP-ET0model (0.134 mm/d) was smaller than that of ANFIS-ET0model (0.188 mm/d) which means that the prediction accuracy was higher for the former model. The average relative error of the ANFIS-ET0model (16.92%) was less than that of the BP-ET0model (32.13%) which showed higher stability of the ANFIS-ET0model. The input items of the two forecast models can be obtained from the current short-term weather forecast factors without special measuring equipment and the procedure is simple, thus it has high practical value and provides a theoretical basis for real-time irrigation forecasting.

ET0; BP neural network; ANFIS; weather forecast factor; Real-time irrigation forecasting; Penman Monteith

LIN Jian-hui, E-mail: linjianhui@bjfu.edu.cn.

S161.4

A

1000-0275（2017）02-0307-08

10.13872/j.1000-0275.2017.0016

余江斌, 林剑辉, 高大帅. 基于天气预报的参考作物蒸发蒸腾量预测模型[J]. 农业现代化研究, 2017, 38(2): 307-314.

Yu J B, Lin J H, Gao D S. Forecast model of reference crop evapotranspiration based on weather forecast[J]. Research of Agricultural Modernization, 2017, 38(2): 307-314.

北京林业大学中长期发展方向立项项目(2015ZCQ- GX-03)；北京市科技计划项目(Z161100000916012)。

余江斌(1993-)，男，安徽安庆人，硕士研究生，主要从事林业智能检测与信息处理方向研究，E-mail：stefenief@bjfu.edu.cn；通讯作者：林剑辉(1978-)，男，福建建瓯人，博士，副教授，主要从事林业生态信息采集与处理研究，E-mail：linjianhui@bjfu.edu.cn。

2016-10-20，接受日期：2017-01-13

Foundation item: Long-term Development Project of Beijing Forestry University (2015ZCQ-GX-03); Beijing Science and Technology Project (Z161100000916012).

Received 20 October, 2016; Accepted 13 January, 2017