两相两重四象限变流器的控制方法及实现

马　驰

(中国铁道科学研究院 机车车辆研究所，北京　100081)

近年来随着电气化铁路的发展，尤其是高速动车组及大功率电力机车的快速发展，采用四象限变流器和三相脉冲宽度调制(PWM)逆变器构成的交-直-交电力牵引传动系统已成为国、内外电力机车技术的发展趋势。

受开关器件技术条件的限制，单相单重四象限变流器在输出更大功率时其主电路仍只能选用低开关频率的开关器件，这就导致在牵引电网侧产生大量低次谐波，给牵引电网带来污染。为解决此问题，可采用多重化四象限变流器的主电路，即将至少两重四象限变流器进行并联，并分别对每重四象限变流器的输入电流进行控制，从而达到既可减小牵引电网侧的谐波含量、亦可减半对开关器件所需承受电流的要求。

对多重四象限变流器的控制目标有2个：一是为三相PWM逆变器提供稳定的直流电压，并保证牵引电网侧的功率因数接近单位功率因数；二是降低牵引电网侧低次谐波含量。为实现这2个控制目标，一是采用电压外环、电流内环的双闭环控制方法，其中常用的电流内环控制方法有瞬态直接电流控制[1]、预测电流控制[2]、滞环电流控制[3]、基于坐标变换的电流控制[4]等方法，前3种方法由于均直接使用采样得到的交流电流，因此对电流传感器的采样精度、采样速率及开关器件的开关频率要求较高，而基于坐标变换的电流控制方法由于将采样得到的交流电流转换为直流电流，具有可以保证控制系统稳态误差小、动态响应快的优点，因此理论上对大功率、低开关频率变流器更为适用；二是采用正弦波脉宽调制(SPWM)技术和载波移相技术，可通过增加硬件设备实现或根据变流器的开关频率进行计算实现。

本文以目前广泛应用的两相两重四象限变流器(简称变流器)为研究对象，研究采用双闭环控制时基于坐标变换电流内环控制方法对大功率、低开关频率变流器的适用性，提出无需增设硬件且适用于多种开关频率变流器的载波移相控制方法，并利用DSP(Digital Signal Processor)微处理器进行控制软件设计，以实现对变流器的控制；再在背靠背功率互馈试验台上对控制方法的控制效果进行验证。

1　数学模型

为了分析如何根据变流器主电路的电气特性以实现对其控制，需要对变流器主电路进行数学建模。变流器的主电路如图1所示。图中：unp为牵引变压器原边电压(简称网压)；inp为牵引变压器原边电流(简称网流)；un1和un2分别为牵引变压器2个次边绕组的电压(简称绕组电压)；in1和in2为变流器的两重输入电流；us1和us2分别为变流器的两重调制电压；Ln1,Ln2和Rn1,Rn2分别为牵引变压器二次侧的漏电感(简称漏感)和线路电阻；L2和C2分别为构成二次滤波电路的电感和电容；D11, D12, D13, D14, D21, D22, D23, D24为IGBT开关器件；Cd为直流支撑电容；Ud为中间电路电压(简称中间电压)；负载为PWM逆变器；io为负载电流。

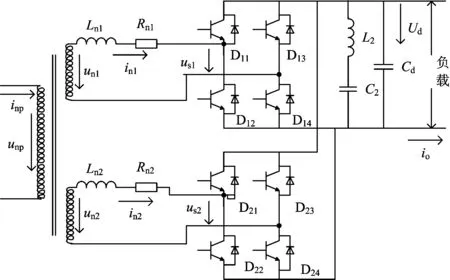
图1　变流器主电路

为避免重复建模，考虑到变流器的两重输出为同一中间电压(即为三相PWM逆变器提供的稳定直流电压)，输入为来自同一牵引变压器的2个次边绕组，理想情况下两重输入电流平均分配，且可通过跟踪网压相位保证两重输入电流的相位一致，因此建立变流器的数学模型时仅需考虑其中的某一重，即忽略图1中表示各变量符号的下标1和2。根据基尔霍夫电压定律，变流器某一重所需的调制电压us为

(1)

假设换相过程为理想状态，无功率损失，根据基尔霍夫电流定律，可以得到

(2)

式中：E2为二次滤波电路存储的能量。

2　控制方法

2.1　基于坐标变换思想的四象限控制

由式(1)与式(2)可知，要最终实现变流器对中间电压的控制，并保证牵引电网侧的单位功率因数，控制器需要计算得到合适的调制电压，可在采集中间电压、输入电流实际值的情况下，采用电压外环、电流内环的双闭环控制方法计算调制电压。

采用基于坐标变换的电流内环控制方法时，首先在静止笛卡尔坐标系αβ下构建变流器正交旋转的电压分量unα=Uncos(ωt),unβ=Unsin(ωt)和电流分量inα,inβ； 然后以ω为旋转角速度，利用坐标变换将其旋转到旋转笛卡尔坐标系dq下，成为直流的电压分量Und=Un,Unq=0和直流的电流分量Ind,Inq；再带入式(1)，可得旋转笛卡尔坐标系dq下的调制电压Usd和Usq分别为

(3)

同理，忽略二次滤波电路存储的能量，通过坐标变换和式(2)可得

(4)

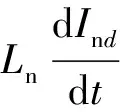
调制电压us可由Usd和Usq通过坐标反变换得到。

文献[4]、文献[5]和文献[7]在采用基于坐标变换的电流内环控制方法设计变流器的四象限控制框图时，忽略了对线路电阻的考虑，这是因为一是认为变流器的负载为电阻，不存在负载功率大幅波动的问题，二是认为线路电阻很小，可以忽略。但在实际应用中，由于变流器的负载为三相PWM逆变器，其具有功率等级高且功率会大幅波动等特点，反映到式(3)中，当负载功率产生大幅波动时，输入电流Ind与Inq也会出现大幅波动，因此即使线路电阻阻值不大，但因为其与输入电流相乘得到的RnInd和RnInq两项是构建式(3)的微分项，即用于PI调节器的前馈之一，有助于降低PI调节器的负担，减少PI调节器输出调制电压的补偿量，所以如果在实际应用中对线路电阻予以忽略，则需要PI调节器输出更多的调制电压补偿量，这又会导致控制系统的动态响应性能降低。综上，设计控制方法时本文保留了对线路电阻的考虑。

根据以上结论，设计变流器的四象限控制框图如图2所示。

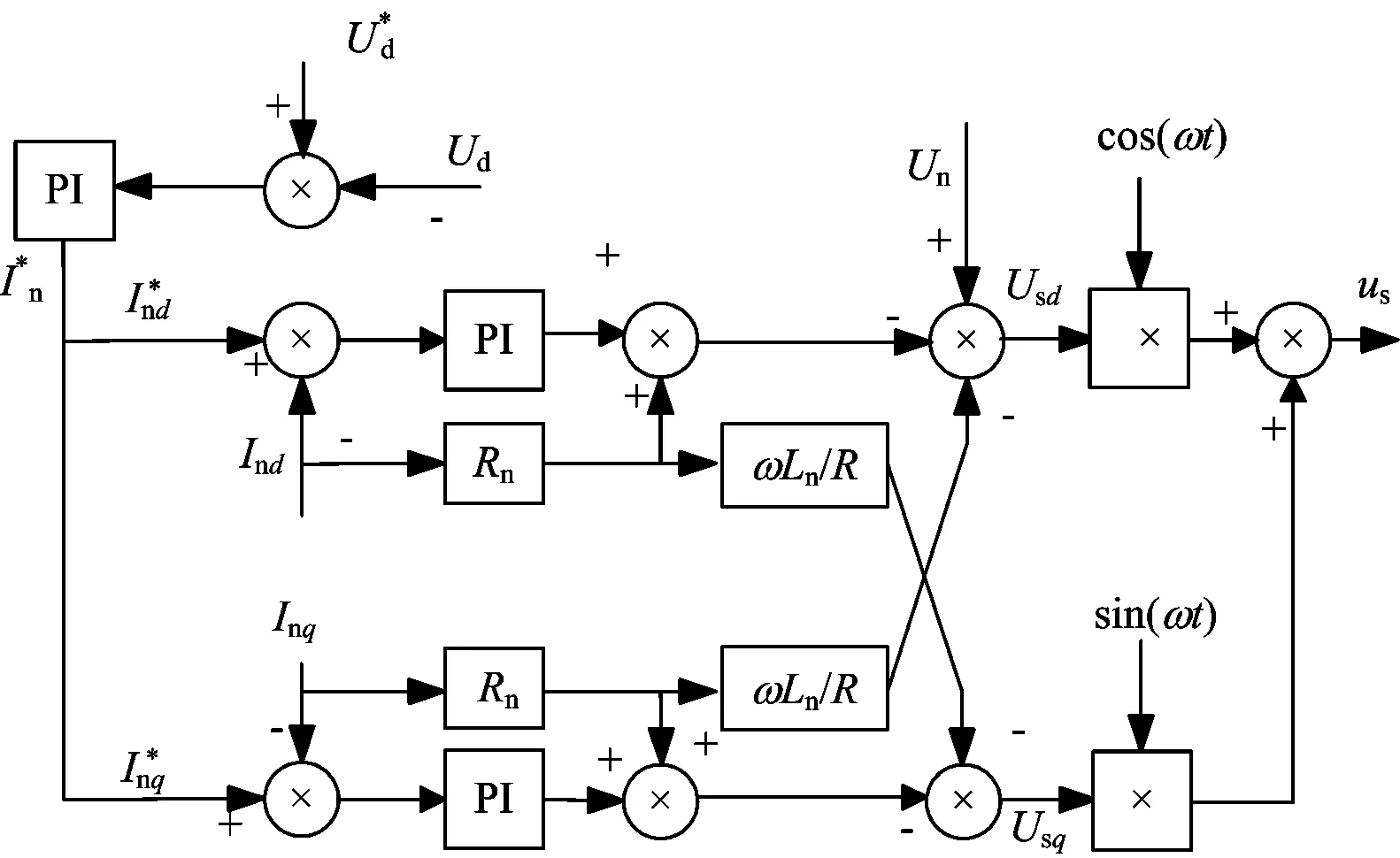
图2　四象限控制框图

2.2　SPWM调制和基于倍增控制频率的载波移相方法

通过以上双闭环控制方法得到所需的调制电压us后，可通过PWM调制将其转换成等效的脉冲波形，并将调制脉冲发送给变流器的开关器件，从而实现对变流器的控制。常用的PWM调制实现方式有多种[8]，考虑到本文研究的为大功率、低开关频率的变流器，同时还需要降低变流器的电磁干扰及对开关器件的损耗，因此选取单极性SPWM技术以实现对调制电压进行PWM调制。

对于变流器中的某一重，根据单极性SPWM技术调制出的调制电压有等幅不等宽的脉冲，会导致在输入电流中产生谐波分量，呈现为叠加了锯齿脉动的正弦波形。每出现1次调制电压的正跳变，输入电流就会产生相应的锯齿脉动，而每出现1次调制电压的负跳变，输入电流就会出现与调制电压正跳变时相反的锯齿脉动。因此，采取载波移相技术减小变流器低开关的频率对牵引电网产生的谐波污染，即对调制电压的SPWM三角载波进行90°移相，尽可能久地错开两重调制电压发生跳变的时机，从而部分抵消两重输入电流的锯齿脉冲，降低牵引电网的谐波污染。变流器的载波移相和SPWM调制原理如图3所示。图中：Tc为SPWM三角载波周期；uc1,uc2为变流器两重调制电压的SPWM三角载波(假设工作在稳态时，us1=us2)。根据文献[7]的研究，载波移相后可消除牵引电网上3倍于开关频率及以下次的网流谐波。

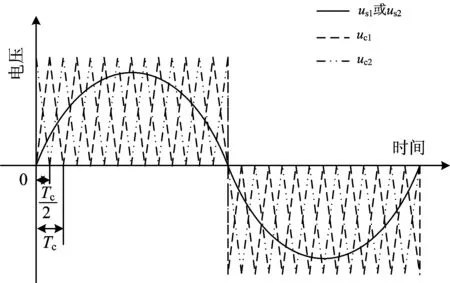
图3　变流器的载波移相和SPWM调制原理

载波移相和SPWM调制的传统实现方法有2种：一种如文献[9]，利用信号发生芯片生成相互错开相位90°的SPWM三角载波，再传入控制器中对调制电压进行SPWM调制，虽然这种方法可以保证SPWM三角载波错相角度的精确性，但是需要增设硬件芯片，从而导致控制系统成本的增加和可靠性的降低；另一种如文献[10]，在离线仿真中利用信号发生器产生SPWM三角载波并进行移相，该方法仅适用于离线仿真，且如果直接将仿真结果用于实际控制时，也不适用于以多种开关频率工作的变流器。

为了解决以上问题，本文提出通过倍增控制频率进行载波移相的方法。具体如下：首先，通过软件使同步控制器的控制周期Ts起始时间与SPWM三角载波周期Tc起始时间(传统方法中，通常控制周期Ts与载波周期Tc无关)，使得控制周期Ts等于载波周期Tc；然后，将控制周期Ts一分为二，即将控制频率fs倍增，分割出的第1个子控制周期用于产生第1重变流器所需的调制电压脉冲，第2个子控制周期用于产生第2重变流器所需的调制电压脉冲，如此便可保证变流器的两重所使用的SPWM三角载波严格互错相位90°，从而达到无需增设硬件即可实现载波移相和可适用于多种开关频率变流器的目的。

3　控制软件

将以上控制方法应用在实际控制器的软件开发中。硬件平台选用TMS320F28335型DSP芯片，该芯片具有150 MHz的时钟频率以及32 K×16 bit的片载随机存储器(RAM)，且内置了1块支持32位单精度浮点计算的浮点处理单元(FPU)、16路增强脉宽调制(ePWM)模块及3路串行通信接口(SCI)。

在使用TMS320F28335芯片作为控制核心时，设计的控制软件分为3大部分：初始化程序、串行通信服务程序、定时中断程序。其中初始化程序主要包括以下4个部分：

(1)设定控制器变量初始值；

(2)配置变流器主电路的参数；

(3)初始化TMS320F23885芯片各模块；

(4)配置定时中断及串行通信服务中断。

串行通信服务程序执行与上位机的串口通信功能，通过SCI接收来自上位机的中间电压指令值、脉冲激活使能等命令，还可通过SCI发送DSP读取的各电流、电压数据，以供上位机进行监视。

定时中断程序是控制软件的主要执行程序，按照控制频率倍增的载波移相控制方法，将定时中断程序的触发周期设定为载波周期的二分之一，当定时中断程序触发后，在采集电压电流传感器信号的基础上，实现基于坐标变换的双闭环控制，并结合ePWM模块实现SPWM调制。定时中断程序流程如图4所示。

图4　定时中断程序流程图

为利用ePWM模块实现SPWM调制，需要在定时中断程序内根据双闭环控制方法计算出的调制电压及频率，在ePWM模块中对PWM周期、PWM比较值、死区时间、载波类型等进行配置，使模块生成SPWM脉冲波形，并通过DSP芯片的ePWM针脚输出，从而控制变流器主电路的开关器件。

由图4可见，控制软件具备故障诊断与保护功能，当检测到发生过压、过流、欠压、输入电流或中间电压实际值与给定值严重不符等情况时，会通过ePWM模块主动锁闭DSP芯片ePWM针脚的脉冲输出，待变流器具备重新上电的条件时才解锁脉冲输出。

4　试验结果及分析

为验证本文控制方法和控制软件的功能和性能，在背靠背功率互馈试验台上进行试验。变流器带三相PWM逆变器作为其负载，三相PWM逆变器驱动电机运行；试验台采用8台电机两两对拖方式运行，其原理如图5所示，试验时的被试牵引传动系统主电路的主要参数见表1。

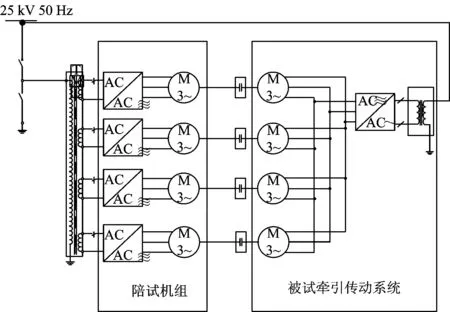
图5　背靠背功率互馈试验台原理图

参数数值牵引变压器变比25000V/1900V线路电阻Rn015Ω漏感Ln302mH直流支撑电容Cd3200μF中间电压Ud3150V(牵引工况)3300V(制动工况)变流器输出功率1600kW(牵引工况)1200kW(制动工况)变流器开关频率350Hz

为考察变流器的启动性能，得到其启动工况下输入电流in1的时程曲线如图6所示。由图6可见：变流器启动时，输入电流变化平稳，没有出现冲击现象。

为考察变流器的大功率运行性能及牵引电网侧功率因数的控制，进行加载测试，先后在牵引工况和制动工况下分别加载至满载(1 600和1 200 kW)，测试得到满载时网压和网流的时程曲线，如图7所示。由图7可见：网压unp与网流inp在牵引工况下的相位相同，在制动工况下的相位相反，可实现能量的双向流动，且以单位功率因数运行。

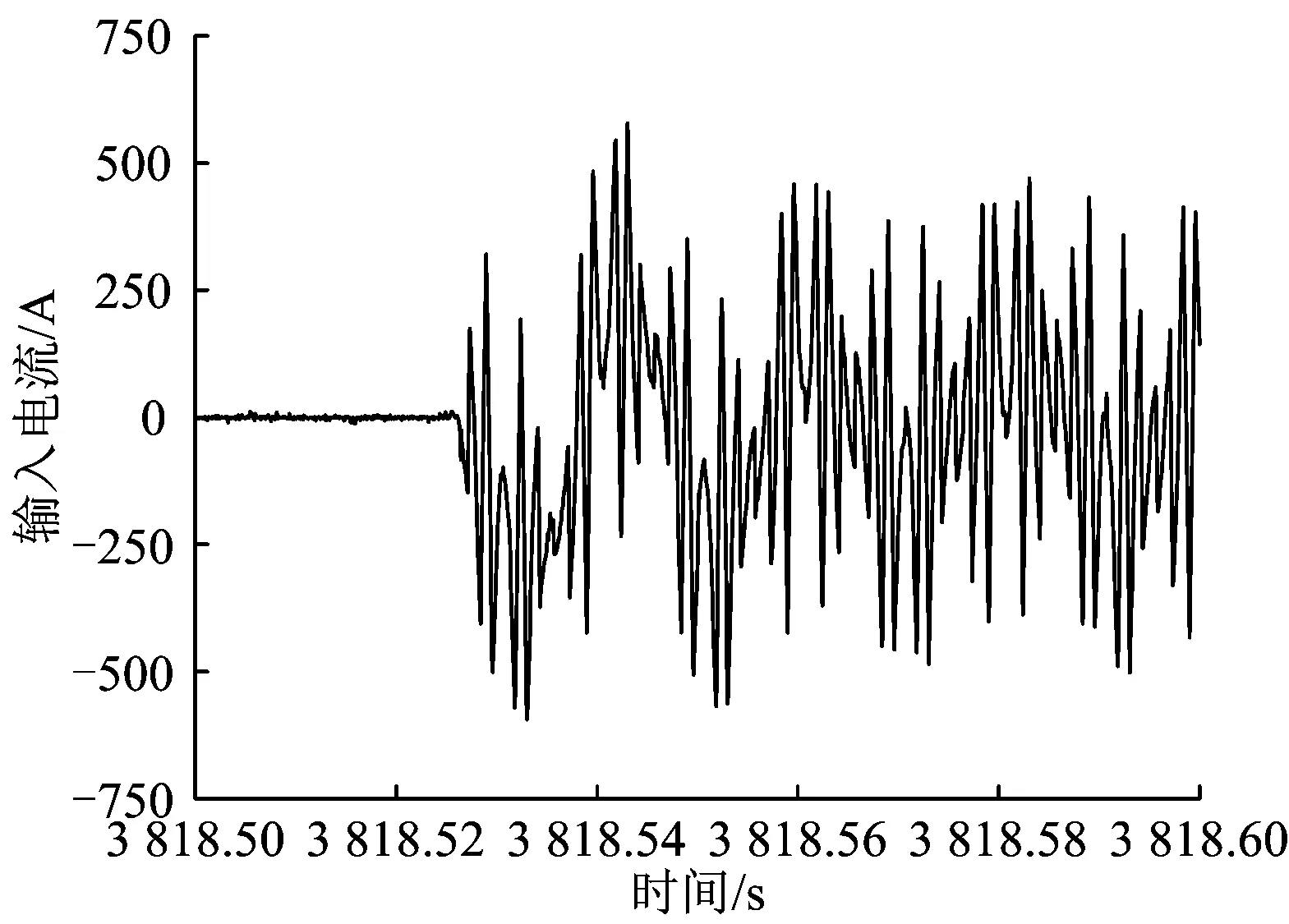
图6　启动工况下输入电流in1的时程曲线

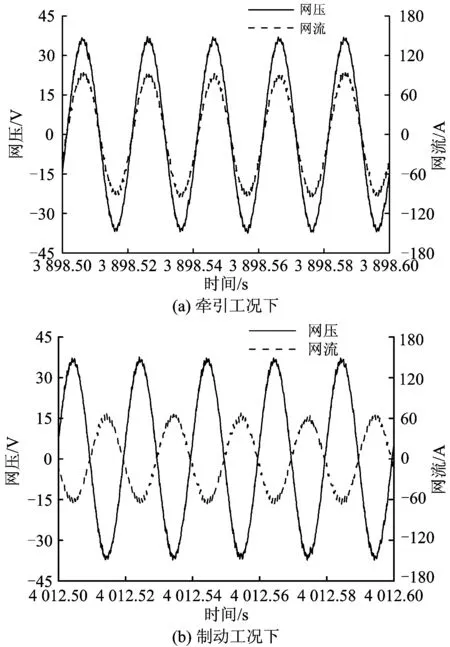
图7　不同工况下满载时的网压和网流

为考察变流器控制方法的稳态和动态性能，记录加载测试时中间电压和输入电流in1的时程曲线，如图8所示。测试结果显示，满载稳态下中间电压Ud的波动平均值约为60 V，最大值约为90 V，计算得出中间电压的稳态波动系数约为1.9%，输入电流in1无异常波动，说明控制系统的稳态误差小；当负载功率动态变化时，虽无法实现文献[4—5](文献[7]无动态响应的测试结果)仿真中的快速加载，但由加载测试测得的中间电压的最大波动变化率约为3.15%，远低于文献[4—5]仿真测试所得的中间电压的波动变化率(约16.7%和20%)，且当中间电压预置值变化时，中间电压也迅速变化且无明显超调，试验全过程中输入电流的变化平稳，说明控制系统的动态响应快。

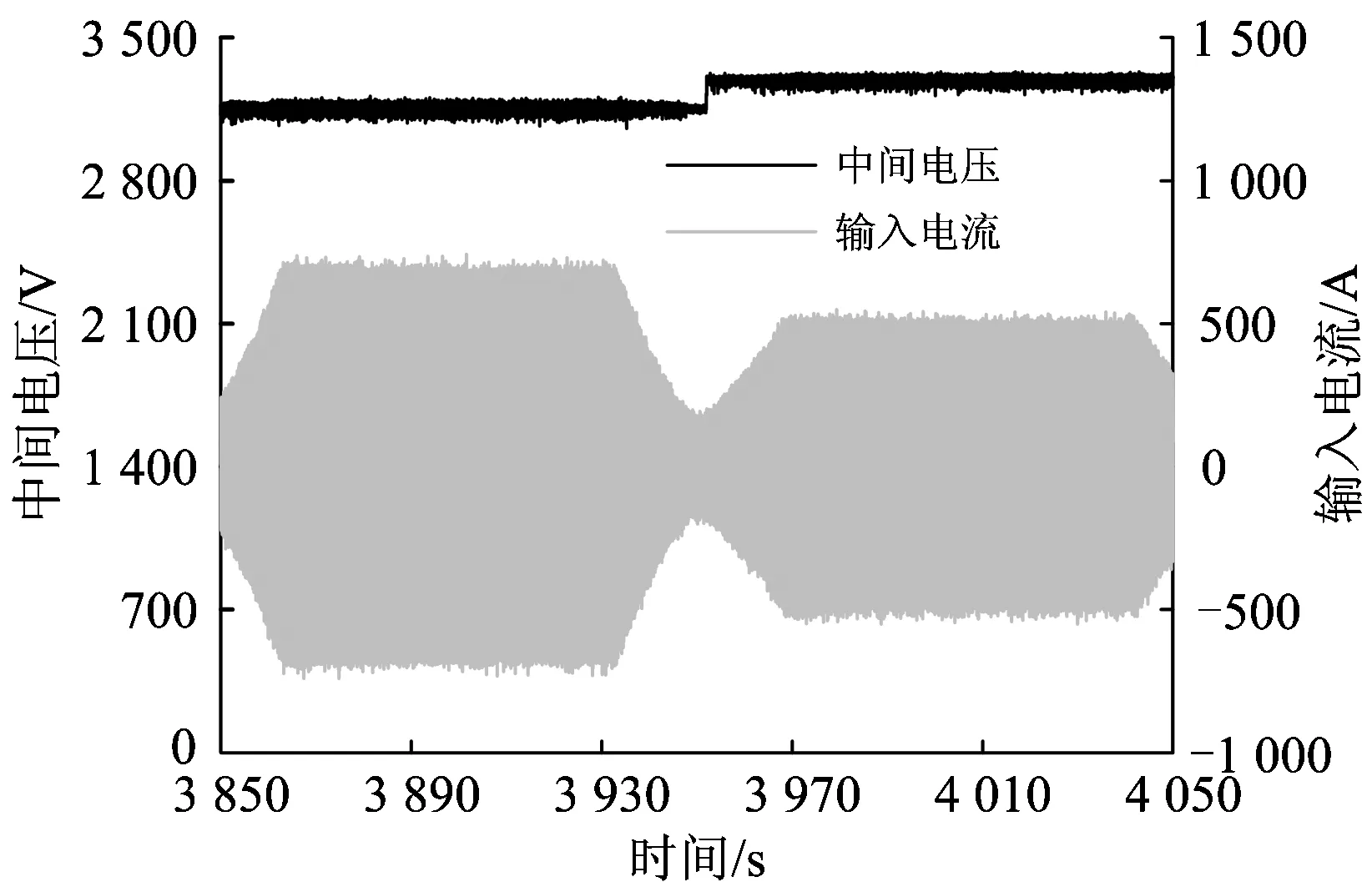
图8　加载测试时的中间电压和输入电流

为考察基于控制频率倍增实现载波移相SPWM的效果，两重输入电流in1和in2的波形对比如图9所示。由图9可见：两重输入电流的脉动峰谷基本相抵，可有效降低网侧电流的谐波含量。

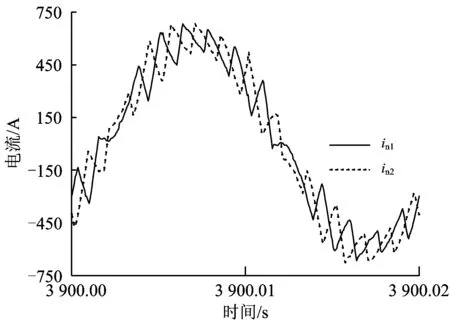
图9　两重输入电流的波形对比

为考察载波移相后低次谐波的减少效果，分别对单重四象限变流器的输入电流in1和网流inp进行谐波分析，计算得到的7～30次谐波与基波比例如图10所示。由图10可见：21次及以下的低次谐波含量基本消除。

图10输入电流in1和网流inp的7～30次谐波与基波比例

计算得到输入电流in1和网流inp的总谐波失真率分别为16.34%和3.21%，可见按照设计的控制方法进行载波移相后，牵引电网侧低次谐波大幅减小。

5　结　语

本文为控制两相两重四象限变流器，采用了电压外环、基于坐标变换的电流内环的双闭环控制方法，且在电流内环控制中对线路电阻予以考虑，并设计了基于倍增控制频率的载波移相和SPWM调制控制方法，将2种控制方法应用在大功率、低开关频率的两相两重四象限变流器主电路上，经过背靠背功率互馈试验台的验证，表明变流器可正常发挥所需功率，实现能量的双向流动，而且以单位功率因数运行，稳态误差小，动态响应快。基于控制频率倍增实现的载波移相SPWM调制方法可很好地保证移相角度的准确，并有效降低了牵引电网侧的低次谐波成分及总谐波失真率。

[1]邹仁. 四象限变流器瞬态电流控制的仿真研究[J]. 机车电传动,2003(6):17-20.

(ZOU Ren. Simulation Study on Transient Current Control of Four Quadrant Converter[J]. Electric Drive for Locomotives,2003(6):17-20. in Chinese)

[2]李伟,张黎. 交—直—交传动系统网侧变流器预测电流控制方法的计算机仿真及实现[J]. 中国铁道科学,2002,23(6):49-54.

(LI Wei,ZHANG Li. Implementation and Computer Simulation of a Converter Control for AC-DC-AC Driver System[J]. China Railway Science,2002,23(6):49-54. in Chinese)

[3]MASWOOD Ali I, LIU Fangrui. A Unity Power Factor Front-End Rectifier with Hysteresis Current Control[J]. IEEE Transactions on Energy Conversion, 2006,21(1):69-76.

[4]MIRANDA U A, ROLIM L G B, AREDES M . A DQ Synchronous Reference Frame Current Control for Single-Phase Converters [C] //2005 IEEE 36th Power Electronics Specialists Conference. Recife: IEEE, 2005:1377-1381.

[5]李伟. 基于坐标变换的单相4象限整流器控制[J]. 电气传动, 2011,41(10):33-36.

(LI Wei. Single-Phase 4 Quadrant Rectifier Control Based on Coordinate Transformation[J]. Electric Drive,2011,41(10):33-36. in Chinese)

[6]SUH Y, TIJERAS V, LIPO T A. A Nonlinear Control of the Instantaneous Power in dq Synchronous Frame for PWM AC/DC Converter under Generalized Unbalanced Operating Conditions[C]// Industry Applications Conference, 2002. 37th IAS Annual Meeting. Conference Record of the Volume 2. Pittsburgh: IEEE, 2002:1189-1196.

[7]范声芳,熊键,张凯,等. 大功率机车牵引四象限变流器解耦控制方案[J]. 中国电机工程学报， 2012，32(21):63-70.

(FAN Shengfang,XIONG Jian,ZHANG Kai,et al. A Decoupling Control Scheme of High Power Four-Quadrant Converters for Traction[J].Proceedings of the CSEE,2012,32(21):63-70. in Chinese)

[8]GRAHAME Holmes D, THOMAS A Lipo. Pulse Width Modulation for Power Converters: Principles and Practice[M]. Piscataway：IEEE Press, 2003.

[9]占奇志,董文娟,卓放,等. 采用二重化技术实现的谐波电压源研制[J] .电力电子技术,2006,40(5):1-3, 12.

(ZHAN Qizhi,DONG Wenjuan,ZHUO Fang,et al. Study of Harmonic Voltage Source with Dual PWM Controller[J]. Power Electronics,2006,40(5):1-3,12. in Chinese)

[10]NADERI R， RAHMATI A. Phase-Shifted Carrier PWM Technique for General Cascaded Inverters[J]. IEEE Transactions on Power Electronics, 2008, 23(3):1257-1269.