基于微积分滑模控制策略的钻机旋转系统

张荣++高景景

摘要：由于钻井的复杂多变，并且在钻井过程中振动会导致钻头的磨损或者失速从而会增加钻井成本，因此要提高钻机对钻进的控制能力，降低能量损耗就需要有合适的控制方法，以微积分滑模控制的理论性研究为基础，设计微积分滑模控制器通过李雅普诺夫来分析钻机旋转系统的稳定性。利用仿真验证可靠性。

关键词：钻机旋转系统；微积分滑模控制；李雅普诺夫

中图分类号：TM383 文献标识码：A 文章编号：1009-3044（2017）04-0258-02

在整个钻井的进程中容易产生有害振动，如钻井过程中地层与岩石的变化、钻杆长度的增减、钻杆组件间及钻杆和底层之间的摩擦力等等，这些危害不利于钻井过程顺利的展开。因此钻机旋转控制系统中引入控制算法是一个切实有效的方法，通過理论的分析，有些控制算法可以抑制钻机有害振动，使钻机旋转系统具有较好的稳定性同时具备良好的动态和静态性能。

由此本文提出了微积分滑模控制，这种复合控制结合了滑模控制和微积分控制的优点，并能够提高闭环系统的性能。

1 微积分滑模控制的理论基础

在一般的滑模变结构控制中，当系统的轨迹到达切换面时，惯性使得运动点穿越切换面也就是说跟踪误差越接近于零过程中切换函数的值会不停的变化，从而造成系统产生了振动。因此，我们需要在系统中增加非线性微分的控制，使得当跟踪误差绝对值趋近于零时，加大微分系数，以此来控制系统中造成的震动，反之当跟踪误差趋于无穷时则减小微分系数。通过对非线性微分的控制，来提升系统响应的快速性，加大系统阻尼，减小系统振动。

非线性系统标准n阶非线性参数不确定系统：

式中n=1，2…m-1，xn及xm为系统状态变量，u为系统输入， y为系统输出，d（t）为外部干扰，f（x）、g（x）均为已知函数，且对任意的x，[Bg（x）≠0]；A，B为系统不确定函数。

针对n阶线性参数不确定系统而设计微分控制器为：

其中f（e）为非线性函数，满足以下条件：

（1）对于任意e，都有[f（e）>0]；

（2）当[e>0]时，[f（e）]为减函数；当[e<0]时，[f（e）]为增函数。

其中[ζ]为无穷小量。

由式（1-9）可得，系统滑模运动存在且稳定。同时可得系统传递函数为：

其中[X1（s）]、[Yd（s）]分别为输入yd和输出x1的拉普拉斯变换。

2 微积分滑模控制器设计

当滑模变结构控制中误差趋近于零时，随着切换函数值的不断增大系统震动会增大，此时难以保证积分滑模控制的特性，并且造成钻头的有害震动。因此为了避免这一问题的产生，同时让切换的函数值更加稳定，可对切换函数进行非线性微分控制，以此来减小系统振动，提升系统响应的稳定性和快速性，

微积分滑模控制器为：

其中ε，h为正常数。

当[t→∞]时，[s→0]，跟踪误差e逐渐增大微分系数f（e）逐渐减小，当微分作用变弱，减小了系统的阻尼性，可以抑制切换函数逐渐增大时系统所产生的振动。相反，当跟踪误差e接近于0时，微分系数f（e）逐渐增大，微分作用随之变强。

3 系统的稳定性分析

稳定性是评判钻机旋转系统是否稳定的重要特征，同时良好的稳定性能能有效抑制钻机有害振动，保证钻机的正常工作，减小钻井设备的磨损。

以下对微积分滑模控制系统进行李雅普诺夫稳定性分析[13][14]。

选择基于切换函数的正定李亚普诺夫（Lyapunov）函数V：

由（1-14）可得，V（0）=0且函数V具有连续一阶导数。对公式（1-14）求一阶导可得：

由上式可推出，当s=0时，[V=0]；否则，[V<0]。因此可知[V]为负半定，[V=ss≤0]，所以滑模运动存在。

当[s→∞时，V=12s2→∞]。

由李亚普诺夫稳定性条件可得系统是稳定的且稳定于s=0的条件。

4 系统仿真及结果分析

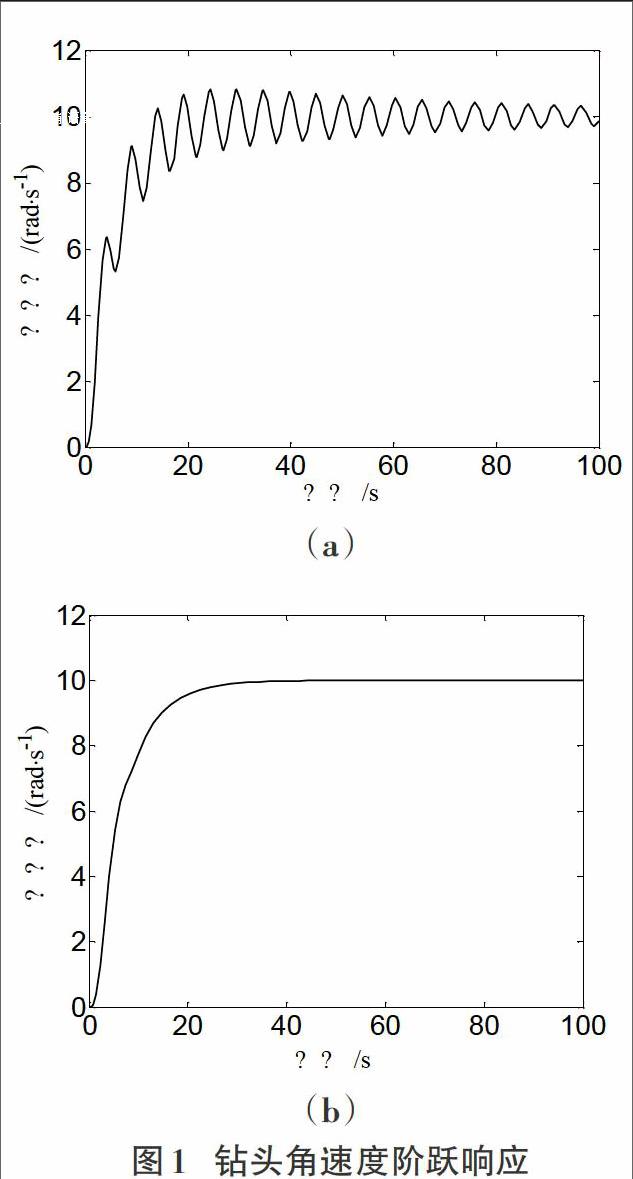
对钻机旋转系统进行仿真分析，仿真过程引用的钻机典型参数。如图1（b）所示为微积分滑模控制的钻机旋转系统阶跃响应。仿真过程中，微分控制器参数h=0.2，ε=0.0001，积分滑模的控制器参数ki=0.12，c1=0.85，c2=0.79。

从图1（b）可得出，与原本系统钻头角速度的阶跃响应图1（a）相比，系统钻头加速的过程中震动非常小。钻头角速度的上升时间为tr=17s，调节时间为ts=24s，系统超调和稳态误差接近于零，由此可看出在抑制粘滑振动的同时系统动态性能和静态性均能得到提高。

5 结论

微积分滑模控制结合了积分滑模控制和非线性微分控制等两种控制方式，可以提高系统的鲁棒性的同时可以控制精确性，并且可以通过减小切换函数值的方法使得系统不断变化而增加的系统振动，从而提高系统响应的快速性和稳定性。

参考文献：

[1] 胡寿松.自动控制原理（第四版）[M]. 北京：科学出版社，2001.

[2] 周东华.非线队系统得自适应控制导论[M]. 北京：清华大学出版社，2002.

[3] 李琳，努尔扎提，张奇志.钻机旋转系统的自适应PID控制[J]. 石油学报，2011，32（1）：158-161.

[4] 刘金棍.滑模变结构控制MATALAB仿真[M]. 北京：清华大学出版社，2005.

[5] 王其福.钻进过程监测与控制硬件系统的研究及应用[D]. 中国地质大学硕士学位论文，2007.1-79.

[6] 雷蓓.交流变频钻机旋转系统控制方法研究[D]. 西安石油大学硕士学位论文，2012.1-79.

[6] 管成，朱善安.一类非线性系统的微分与积分滑模自适控制及其在电液伺服系统中的应用[J]. 中国电机工程学报，2005， 25（4）： 103-108.

[7] 努尔扎提.基于滑模控制的钻机旋转系统及其监控[D]. 西安石油大学硕士学位论文，2011：1-79.