Homomorphic Error-Control Codes for Linear Network Coding in Packet Networks

Xiaodong Han, Fei Gao＊

Department of Information and Electronic Engineering, Beijing Institute of Technology, Beijing 100081, China

* The corresponding author, email: gaofei@bit.edu.cn

I. INTRODUCTION

Network coding allows participating nodes in a network to encode incoming data packets instead of simply forwarding them, which makes it possible to achieve the maximum information flow in the multicast networks[1-3]. Moreover, linear coding is enough to achieve the maximum flow upper bound in multicast network with one or more sources[4]. Random linear network coding is even more powerful because the intermediate nodes in the network can perform linear encoding by randomly choosing their local encoding coefficients without any knowledge of the network topology to achieve the multicast capacity [5].Due to these great advantages, linear network coding and random linear network coding are useful in many areas: for example, they can be used in networks to disseminate information efficiently [6, 7], or in distributed data storage system to save storage space [1, 8], and so on.

Regardless of the benefits that network coding offers to the network, when the network is composed of channels that are error-prone,network coding performs as a double-edged sword. Explicitly speaking, although encoding the data packets at every intermediate node provides some degree of performance gain,the erroneous packets injected to the network at the intermediate nodes may flow in the network and combine with other packets, so that the problem of deducing the source packets at some intended sink nodes may become a challenging task. To overcome this drawback, network error correction code has been proposed and studied [9-12].

This paper studies homomorphism network error-control design.Specially, it focuses on binary field design since most prevailing code for communication is in binary field instead of high order finite field.

Several approaches have been proposed to design codes that can correct network errors in network coding. Cai and Yeung have introduced network error correction codes and built a series of correction bounds by generalizing classic coding theory to network setting [9,10]. Zhang, Balli et al. have further studied these codes in [11, 13], where they defined the minimum rank of network error correction codes based on error space and deduced the correction capabilities of random linear network codes. On the other hand, Kotter, Kschischang, and Silva [12, 14] have introduced rank metric codes, where the codewords are defined as subspaces of some ambient space.

While these information-theoretic multicast network error correction codes are elegant,they are designed to correct errors at sink nodes. Due to lack of sparsity, the encoding at the source node and decoding at the sink nodes with network error correcting codes proposed in the literature are computationally complex; and since such error correction is operated at receivers, bandwidth consumed by corrupted packets at intermediate nodes will not be reclaimed or reduced. Also, correction at the sink nodes can’t benefit from parallel or distributed computation. Furthermore,network coding is highly susceptible to pollution attacks in which malicious nodes modify packets by design so as to prevent message recovery, so that homomorphic signatures for network coding are used to validate the integrity of signed data and suit binary field distributed storage system [6, 15-20]. With homomorphic signatures, a data packet at any intermediate node that fails to pass the verification will be immediately discarded, regardless the reason for the packet corruption is due to malicious attack or random channel error.As a consequence, it is rather unlikely for an error packet to reach the destination, thus error correction only at the sink nodes becomes infeasible. For conventional method with network coding homomorphic signatures verification, it is readily caused that packets are not integrity so as to sinks unable to receive least correct linearly independent packet lead to decode incapable, further waste resource to retransmission. Moreover, the homomorphism in linear network coding can maintain integrity without destroying packets.

Link by link error correction code solves such problems. However, in classic link by link error correction code, each intermediate node has to pack and unpack the data. Such operations lead to extra bandwidth overhead and latency. Therefore we are motivated to study the homomorphic network error correction code. We will show that, if the source node in linear network coding encodes the source packets with a unified linear block code, then every packet flowing in the network deduced by the source packets satisfies the same encoding constraints as the source packets. The homomorphic checksum manner not only detects error but also correction within the capability of codes. It prevents to consuming extra bandwidth and latency caused by compute-and-forward. It reduces the computational complexity meanwhile improves accuracy of correction.

The remainder of this paper is organized as follows. In Section 2, homomorphic linear error-control code over binary field and its extensions in packet-based linear network coding is studied. In Section 3, three examples about the applications of the proposed homomorphic code are demonstrated to show the practical utility of the homomorphism. Further, we presentation simulation and analysis in Section 4.Finally, conclusions are drawn in Section 5.

II. HOMOMORPHIC LINEAR BLOCK CODING NETWORK CODING

Consider a linear network multicast network coding on a communication network with a source node, a set of intermediate nodes and a few sink nodes. At first, assume that the networkhas a unique source node.The notation V is the vertex set consisting of nodes of the network and E is the edge set whose elements are the communication channels of the network. Assume that the network coding is defined over a finite fieldwhere q and k is a positive integer. That is, we focus on the network coding over the binary extension Galois fieldswhich are widely used in the classic error-correction codes. Furthermore, we assume that the transmission of the data through the network is packet-based.The network coding can be either random or non-random.

To show the homomorphism of the linear network coding, here is a simple example.Take an intermediate node from the network.Assume that the node has two incoming edges and one outgoing edge, as shown in figure 1. The data packet transmitted by the incoming edges areandrespectively.Here the superscript T stands for a transpose and K is the information length. Attached on each incoming edge, there is a checksum of the packet. The checksums of the data packets are transmitted through the network along with the data packets, always experiencing the same network encoding as the data packets. Define the checksum of a vectorwhereare a group of predetermined coefficients overAssume that the local encoding coefficients of the two incoming edges areandrespectively. Since the checksums ofandexperience the same network coding, the checksum of the outgoing edge generated by the local encoding will beOn the other hand, the data packet transmitted by the outgoing edge iswhose checksumcan be verified to beThus for allandthe homomorphic propertyis satisfied. In other words, the checksums of the data packets are homomorphic with respect to the linear network coding.

Based on such an observation, we now investigate the homomorphism of the general linear network coding. Assume that there is an ω-dimension linear network coding on the communication networkover the finite field. The source messages are ω packetseach with lengthwhere for allDefine a linear block codeof blocklength N and rateby a generator matrixof dimension[21, 22]. The source node maps each source packetto a codewordAs known, such a code can also be described by a parity-check matrixof dimension, where. Each row of the parity-check matrix describes a linear constraint satisfied by all codewords. Note that the elements ofandtake values from Fq.The source node then sends the ω codewordsonAccording to[1-3], if the network coding is linear, a data packet transmitted over channelcan be described by (1):

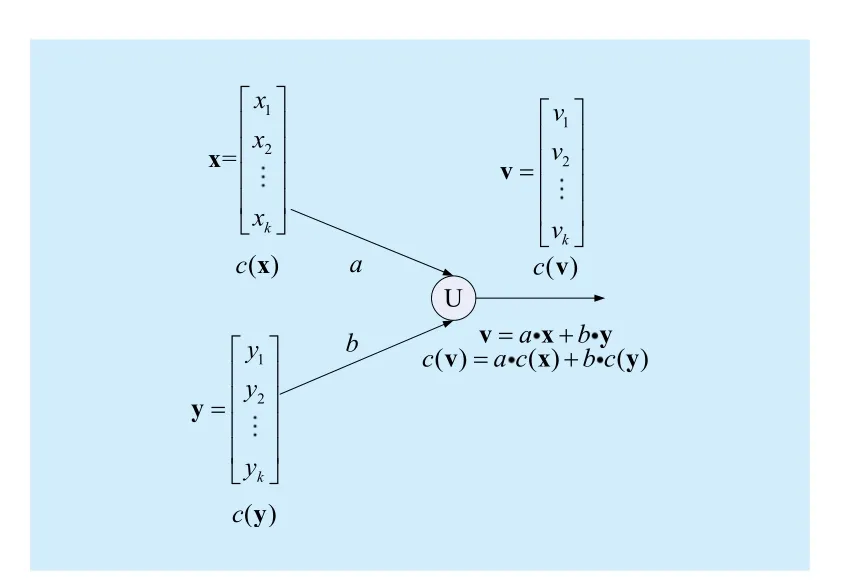
Fig. 1 Homomorphic checksums for linear network coding

The last equality follows fromEq. (2) indicates that, for an error-free linear network coding, a data packettransmitted by any channelwill be a codeword of the linear block code. In other words,a data packet over channelsatisfies the same parity-check constraints as the source linear code of generator matrixand parity-check matrix. As seen, linear network coding does not change the encoding constraints of the linear block coded packets flowing in the network. Thus we call the linear block code is homomorphic with respect to linear network coding.

2.1 Linearly homomorphic block coding

Theorem 2.1: Define a linear network coding overon a unique source node networkIf the source nodeencodes each one of its K-length ω-dimensional source packets to a N-length codeword by anlinear block code of generator matrixand parity-check matrix, whereandareandq-ary matrices respectively,then a data packet over an edgesatisfies the same encoding constraints as the source linear block code of generator matrixand parity-check matrix.

According with the definition of ring homomorphism in abstract algebra,where A is a ring, ifandis called the homomorphism of the ring. While the linear network coding does not change its linear block coding constraint rules, so the transmitted data packets are in accordance with the linear homomorphism check rules.

From Eq. (2), the parity-check matrix can be used to detect or correct errors in the received vector:

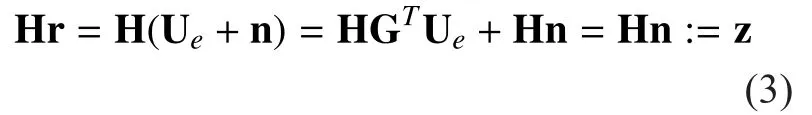
where r is the output vector of channelwhich may be noise polluted. The vector z is referred to as the syndrome. If no malicious attack exists in the network, when the syndrome vector is null, we assume there have been no errors. Malicious attack can be detected by homomorphic signatures for network coding[6, 15, 16], which validates our assumption.Otherwise, when the syndrome is not null, we decode the received vector by finding the most likely error vectorthat explains the observed syndrome given the assumed properties of the channel.

Theorem 2.1 provides us flexible ways to perform network error corrections. The error-correction can be performed link by link,point to point from the source to a sink node,or a mixture of the two ways. In the mixed way, an intermediate network node without enough computation capability can simply forward its network coding packets to its subsequent nodes which may decode the received packets.

As stated, the linear block code for error detection and correction in Theorem 2.1 is defined over finite fieldover which the linear network coding is performed. Hence, the source can use any q-ary linear block codes,such as Reed-solomon codes [21], low-density parity-check (LDPC) codes over[23, 24],and so on. Great advantage of these codes is having efficient encoding and decoding algorithms that allow the computation of the error vector with low complexity. Moreover,due to the algebraic structure or the sparse nature of the parity-check matrix, a linear error detection or correction code can be defined by a group of parameters. Thus in order to decode the packets, one can reconstruct the parity-check matrix based on the parameters at any node of the network, avoiding the multicast of a large-sized parity-check matrix.

As known, the most well-known and the most widely-used error correction codes as Turbo codes and LDPC codes are binary based. Therefore it is natural for us to ask whether a binary linear block code is homomorphic in network coding. To answer this question, confine all the elements ofandwithinLet the data packet transmitted over channelbeNote the network coding is performed overand. For an elementwe write out its binary extension asforLetforThen from Theorem 2.1, we have (4)

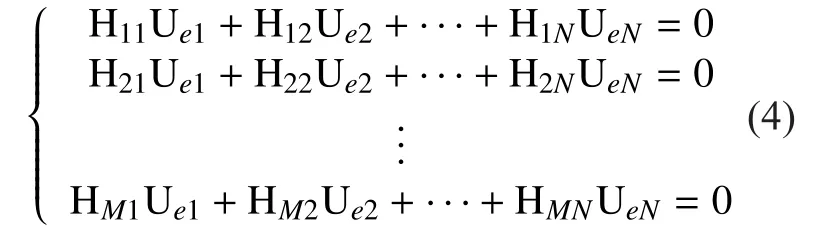
2.2 Linearly homomorphic block coding over binary field

Corollary 2.2: Define a linear network coding overon a unique source node networkwhereand L is a positive integer. If the source nodeencodes each one of its K-length ω-dimensional source packets to a N-length codeword by alinear block code of generator matrixand parity-check matrix, whereandareandbinary matrices respectively, then each sub-code of the packet transmitted oversatisfies the same encoding constraints as the source binary linear block code defined by generator matrixand parity-check matrix. In fact, Corollary 2.2 is rather straightforward because the binary fieldis a subfield of the extension fieldwhen

Corollary 2.2 means that a binary linear block code will be homomorphic in linear network coding when the network coding is defined over a binary extension fieldA binary homomorphic network error-control code is very useful, since all the classic binary linear block codes, such as terminated convolutional code [21], Turbo code [26, 27], LDPC code[22, 28], polar code [29], and so on, along with their efficient encoding and decoding algorithms can be applied to network coding for error detection and correction. Thus we have simply built a bridge between the network error correction and the classic channel coding theory which are rather mature.

At this point, we have studied the homomorphic linear network error-control codes for unique source multicast. The extension of the homomorphic code from unique source to multiple sources is straight-forward. That is,if we replace the unique source by multiple sources in Theorem 2.1 and Corollary 2.2, the conclusions keep valid. For brevity, we omit further details.

III. APPLICATION EXAMPLES

In this section, a combinational use of homomorphic linear code with homomorphic signatures, McEliece public-key cryptosystem and unequal error protection are demonstrated respectively, which verifies the practical utility of the homomorphic linear code.

3.1 Homomorphic linear code with homomorphic signatures

A secure way to prevent pollution attack in network coding is to use homomorphic signatures. Several homomorphic signatures for network coding are available, as in [6, 16].However, these homomorphic signatures make use of groups in which the discrete logarithm problem is hard. They require the network coding coefficients to live in a fieldwhere q is very large. In particular, these schemes can’t support linear operations over small fields such asand its extensions, which means that they are not compatible with the homomorphic error-control codes we are studying here. In [15], linearly homomorphic signatures over binary fields have been proposed. This scheme is defined overso it is compatible with our homomorphic error-control codes.

We now combine the network error correction with homomorphic signatures for reliable and secure multicast. Concretely, our codes work as follows. Assume a linear multicast on the networkoverhas ω-dimension, whereThe source packets are ω vectors :With binary extension, the source message can be described as the following matrix form:

Let α be a primitive element of Fq. Then Fqcan be either expressed asIt is observed that forcan be expressed as Eq. (7)

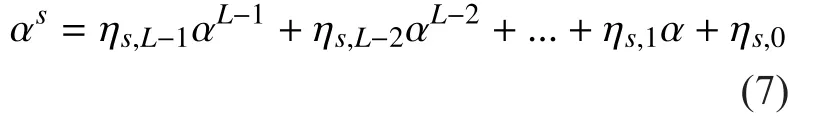
Substitution of Eq. (7) and Eq. (8) into Eq.(1) yields:

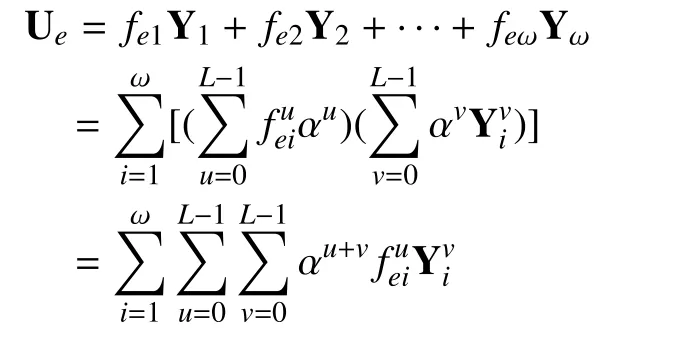
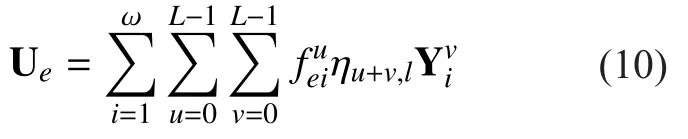
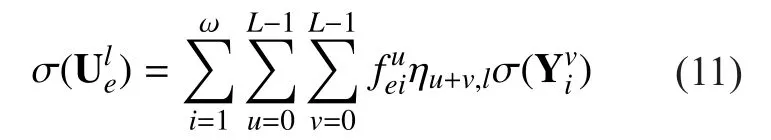
3.2 Homomorphic McEliece publickey cryptosystem

In this sub-section we illustrate the homomorphic properties of McEliece public-key cryptosystem with respect to linear network coding.As known, the McEliece cryptosystem is built on linear error-correcting block codes, thus we use such a code to design a homomorphic public-key cryptography for network coding.

Let’s begin with the construction of “homomorphic” error vector pattern that will be used in the McEliece cryptosystem for network coding. Assume t is a predetermined positive integer number. For a ω-dimension q-valued linear network coding multicast, we will designbinary vectors that span a linear space, in which every vector has Hamming weight no more than t.

Assume Alice has D sink nodesin the networkand a node of Bob wishes to broadcast ω K-length q-valued vectors to these sink nodes. One may imagine that Alice runs a company to collect live-view videos from global mobile users. Alice has D severs distributed around the world.Bob witnesses an interesting scene and he is now uploading the live-view video to the servers. The contents transmitted by Bob are invaluable thus they are protected by McEliece cryptosystem [32]. The nodesshare the same keys which are generated as follows. Alice chooses a binarycode C capable of correcting t errors. This code can be generated by agenerator matrixand possesses an efficient decoding algorithm.For example, this code can be the Goppa code of parameters[33]. In addition, Alice chooses a randombinary non-singular matrixand a randompermutation matrix, and computes thematrix. Finally,Alice publishesas her public key and holdsas her private key.

Assume now Bob has ω vectorsto be broadcasted to the D nodes of Alice. He will then send the messages in the following steps.

(1) Bob expands the source vectorsto binary vectors by writing out their sub-codes as

(2) Bob encodes the messageas a binary vector of length K and computesfor

(4) Bob computes and broadcastsfor

To conclude the discussions above, if the messages at the source node are encrypted with the McEliece cryptography for linear network coding, then any packet over channelis encrypted or protected by the same cryptography.

3.3 Unequal error protection

In some scenarios of multicast network coding, different messages do not have equal rank of importance, thus it is better to protect them separately with unequal error protection(UEP). For example, the global kernel of the packet in network coding needs better protection, since it contains crucial information to recover the original source messages. A global kernel error may affect the decoding at the destination. Another example is when a multi-resolution source code is transmitted over a wireless channel with network coding.Since the coarse resolution contains the basic information to reconstruct at least a crude representation of the intended objects, it should be protected more carefully than the fine resolution.

As seen in Section 2, the classic linear block code is homomorphic in network coding. An unequal error protection design for the classic linear block code is naturally applicable to network coding error correction thus more detailed explanations is omitted. Interested readers please refer to [34, 35].

IV. SIMULATION RESULTS AND DISCUSSION

In this section, we evaluate via simulation the error-correction performance of homomorphic error-control codes for linear network coding over finite fieldFor the butterfly network in figure 2, we made a simulation with homomorphic checksum detection and correction at different nodes in network. We verify the BER(bit error rate) on sink nodesandusing code rate-1/2 Turbo code. Also, we transmit codes from source node to sink nodes with linear network coding scheme over

All depicts for the simulations set light on the BER of sink nodesandwhich(dB) represents the SNR (Signal to Noise Ratio). As seen, the simulation curves of sink nodesandmatch almost exactly for all the schemes because of sink nodesandare symmetric, therefore we analyze one of them.The interaction of the simulation and theoretical curves nearby Y-axis more and more for different scheme which proposed the correction gains increases significantly. Theory curve is the BER obtained by using classic link by link error correction code (i.e., Turbo code of code rate 1/2). First of all, we can observe that the performance of the scheme for correction at sink nodes only is around 0.2dB better than the theory at the BERin figure 3. Meanwhile, a performance gain of around 0.7dB of the scheme for correction at network coding node (node 3 in network) and 1.8dB of the scheme for correction at each node at the same BER in figure 4 and figure 5. Furthermore, our simulation shows that the performance with the scheme of correction at each node is more optimal than theory value when SNR is more than 1dB in figure 5.

In figure 3, the BER performance of the scheme for correction at sink nodes is poorer than the way for classic link by link error correction code in a low SNR regimebecause the error packets are transmitted to destination nodes, which impairs network performance. However, as the SNR increases, the BER improves, and network capacity also increases. While the scheme of link by link error correction code has to pack and unpack, which results in extra bandwidth overhead and lower bandwidth efficiency. Therefore, such scheme can only achieve better capacity in a higher SNR regime

Since the error packets are corrected at intermediate nodes, the BER of the scheme for error checking and correction at intermediate nodes in figure 4 and figure 5, including the scheme of correction at network coding nodes and each node, can be close to the scheme of link by link error correction code in a low SNR regime, especially for the way of correc-tion at each node. The homomorphic checksum method is simpler and less costly, hence it can achieve the BER at a low SNR regime, which the classic scheme needs 10dB to reach. This indirectly illustrates the relationship between the capacity and the SNR according to Shannon’s theorem as well.

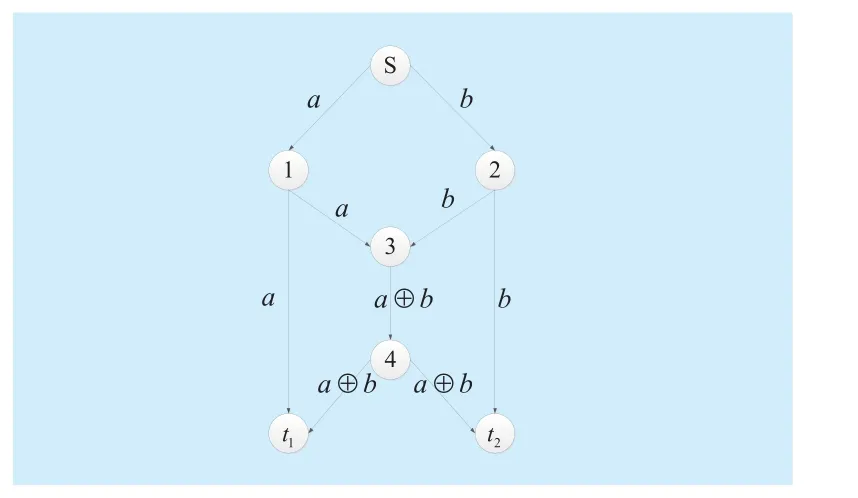
Fig. 2 butterfly network

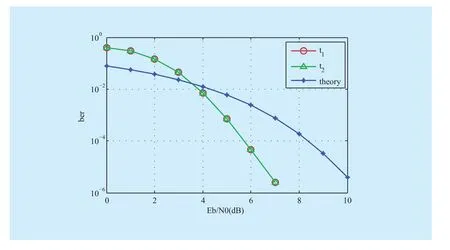
Fig. 3 The scheme of correction at sink nodes

Fig. 4 The scheme of correction at network coding nodes

Fig. 5 The scheme of correction at each node

Compared with simulation results in figure 3 and figure 4, SNR needs more than 3.8dB and 3dB respectively at least is able to make the performance better than theory value. It notes that error performance improves notably for correction at network coding nodes compared with correction at sink nodes only. In other words, our homomorphic error-control codes for linear network coding are able to achieve optimal error performance gain.

V. CONCLUSIONS

In this work, the application of classic linear block code in network coding for network error-control has been studied. Concretely, the homomorphism of the classic linear block code in linear network coding has been shown. Therefore, the code is applicable to detect and correct errors not only in a distributed link by link way, but also in a centralized point to point way, where the error correction is performed at the sink node. Moreover, the binary homomorphic linear error-control code is introduced. Great advantage of the homomorphic property of the network error-control code is that, the classic good binary linear block codes, such as Turbo code and LDPC code, can be directly used in network coding to perform network error control. Furthermore,the proposed code has many applications as the combination with the homomorphic signatures for network error correction and malicious attack prevention, the combination with McEliece public-key cryptosystem for secure multicast, and unequal error protection for different priorities and qualities in a unified multicast, and so on.

ACKNOWLEDGEMENTS

This work was supported by Natural Science Foundation of China (No. 61271258).

[1] Chou, P.A., Wu, Y., “Network coding for the internet and wireless networks”, IEEE Signal Process Magazine, vol.24, no.5, pp 77-85, 2007.

[2] R. Alshwede, N. Cai, S.-Y. R. Li, R. W. Yeung,“Network information flow”. IEEE Transactions on Information Theory. vol.46, no.4, pp 1204-1216, 2000.

[3] R. W Yeung, S.-Y. R. Li, N. Cai, Z. Zhang, “Network coding theory”. (Now Publishers Inc., Boston),pp 411-483,2006.

[4] S.-Y. R. Li, R. W. Yeung, N. Cai, “Linear network coding”. IEEE Transactions on Information Theory. vol.49, no.2, pp 371-381, 2003.

[5] T. Ho, M. Medard, R. Koetter, D. Karger, M. Eff -ros, J. Shi, B. Leong, “A random linear network coding approach to multicast”. IEEE Transactions on Information Theory. vol.52, no.10, pp 4413-4430, 2006.

[6] P. Krishnan, B. Sundar Rajan, “A Matroidal Framework for Network-Error Correcting Codes”. IEEE Transactions on Information Theory. vol.61, no.2, pp 836-872, 2015.

[7] M. Yang, Y. Y. Yang, “Applying network coding to peer-to-peer file sharing”. IEEE Transactions on Computers. vol.63, no.8, pp 1-14, 2013.

[8] X. Li, T. Jiang, Q. Zhang, L. Wang, “Binary linear multicast network coding on acyclic networks:principle and applications in wireless communication networks”. IEEE Journal on Selected Areas in Communications. vol.27, no.5, pp 738-748,2009.

[9] R. W. Yeung, N. Cai, “Network error correction,part I: basic concepts and upper bounds”. Communications in Information and Systems. vol.6,no.1, pp 19-36 , 2006.

[10] N. Cai, R. W. Yeung, “Network error correction,part II: lower bounds”. Communications in Information and Systems. vol.6, no.1, pp 37-54, 2006.

[11] Z. Zhang, “Linear network error correction codes in packet networks”. IEEE Transactions on Information Theory. vol.54, no.1, pp 209-218,2008.

[12] R. Kotter, F. R. Kshischang, “Coding for errors and erasures in random network coding”. IEEE Transactions on Information Theory. vol.54, no.8,pp 3579-3591, 2008.

[13] H. Balli, X. Yan, Z. Zhang, “On randomized linear network codes and their error correction capabilities”. IEEE Transactions on Information Theory. vol.55, no.7, pp 3148-3160, 2009.

[14] D. Silva, F. Kschischang, R. Kotter, “A rank-metric approach to error control in random network coding”. IEEE Transactions on Information Theory. vol.54, no.9, pp 3951-3967, 2008.

[15] D. Boneh, D. M. Freeman, “Linearly homomorphic signatures over binary fields and new tools for lattice-based signatures”. Proceedings of Public Key Cryptography (PKC 2011). Springer LNCS 6571, pp 1-16, 2011.

[16] S. H. Lee, M. Gerla, H. Krawczyk, , K. W. Lee, E.A. Quaglia. “Performance Evaluation of Secure Network Coding using Homomorphic Signature”. International Symposium on Network Coding (NetCod), Beijing, pp 25-27, July, 2011.

[17] C. Cheng, T. Jiang, “An efficient homomorphic MAC with small key size for authentication in network coding”. IEEE Transactions on Computers. vol.62, no.10, pp 2096-2100, 2013.

[18] C. Cheng, T. Jiang, Q. Zhang, “TESLA-based homomorphic MAC for authentication in P2P system for live streaming with network coding”.IEEE Journal on Selected Areas in Communications. vol.31, no.9, pp 291-298, 2013.

[19] C. Cheng, T. Jiang, “A novel homomorphic MAC scheme for authentication in network coding”.IEEE Communications Letters. vol.15, no.11, pp 1228-1230, 2011.

[20] M. Dai, C. W. Sung, H. Wang, X. Gong, Z. Lu, “A new zigzag-decodable code with efficient repair in wireless distributed storage”, IEEE Transactions on Mobile Computers. vol.16, no.5, pp 1218-1230, 2017.

[21] S. Lin, D. J. Costello, “Error control coding: fundamentals and applications”. (Pearson Education, Inc. India), pp 51-84, 2004.

[22] J. Broulim, V. Georgiev, “LDPC error correction code utilization”. The 20th Telecommunications forum TELFOR 2012. Serbia, Belgrade, pp 20-22,Nov, 2012.

[23] K. Huang, D. G. M. Mitchell, L. Wei, X. Ma and D.J. Costello. “Performance Comparison of LDPC Block and Spatially Coupled Codes Over GF(q)”.IEEE Transactions on Communications. vol.63,no.3, pp 592-604, 2015.

[24] B. Rong, T. Jiang, X. Li and M. R. Soleymani,“Combine LDPC codes over GF(q) and q-ary modulation for bandwidth efficient transmission”. IEEE Transactions on Broadcasting. vol.54,no.1, pp 78-84, 2008.

[25] Z. Wan, “Lectures on finite fields and Galois rings”. (World Scientific Publishing Co. Pte. Ltd.New Jersey), pp 49-72, Oct, 2003.

[26] F. Jiang, E. Psota, L.C. Perez, “Decoding Turbo Codes Based on Their Parity-Check Matrices”.IEEE 39th Southeastern Symposium on System Theory (SSST 2007), Mercer University Macon,Georgia, USA, pp 221-224, 04-06 Mar, 2007.

[27] S. Benedetto, D. Divsalar, G. Montorsi, F. Pollara,“A soft-input soft-output maximum a posteriori(MAP) module to decode parallel and serial concatenated codes”. TDA Progress Report, pp 42-121, 1995.

[28] R. G. Gallager, “Low-density parity-check codes”.(MIT Press, Cambridge, Massachusetts), pp 49-54, 1963.

[29] E. Arikan, “Channel polarization: a method for constructing capacity-achieving codes for symmetric binary-input memoryless channels”. IEEE Transactions on Information Theory. vol.55, no.7,pp 3051-3073, 2009.

[30] E. Kehdi, B. Li, “Null keys: limiting malicious attacks via null space properties of network coding”. IEEE International Conference on Computer Communications (INFOCOM 2009). Rio de Janeiro, 19-25 Apr, 2009.

[31] W. Qiao, J. Li, J.Ren. “An efficient error-detection and error-correction (EDEC) scheme for network coding”. IEEE Global Telecommunications Conference (GLOBECOM 2011), Houston, 5-9 Dec,2011.

[32] A. Couvreur, I. M. Corbella, R. Pellikaan, “A Polynomial Time Attack against Algebraic Geometry Code Based Public Key Cryptosystems”. IEEE International Symposium on Information Theory(ISIT 2014), University of Hawaii, USA, 29 Jun-04 July, 2014.

[33] A. Shoufan, T. Wink, H. G. Molter, S. A. Huss and E. Kohnert. “A Novel Cryptoprocessor Architecture for the McEliece Public-Key Cryptosystem”.IEEE Transactions on Computers. vol.59, no.11,pp 1533-1546, 2010.

[34] S. Borade, B. Nakiboglu, L. Zheng, “Some fundamental limits of unequal error protection”.IEEE International Symposium on Information Theory (ISIT 2008) , Toronto, 06-08 July, 2008.

[35] J. Yue, Z.H. Lin, B. Vucetic, “On Estimation of Protection Parameters for Unequal Error Protection Distributed Fountain Codes in Wireless Relay Networks”. IEEE Wireless Communications and Network Conference (WCNC’ 2014), Istanbul, 06-09 Apr, 2014.