Polar-Coded Modulation Based on the Amplitude Phase Shift Keying Constellations
Dekun Zhou, Jincheng Dai, Kai Niu, Chao Dong, Jingyuan Sun, Yi Zhang, Hao Guan
1 Key Laboratory of Universal Wireless Communication, Ministry of Education, Beijing University of Posts and Telecommunications,Beijing 100876, China.
2 Nokia Beijing Bell Lab
I. INTRODUCTION
Different from the Luby transform code in[1]-[3], polar codes [4] are shown to be capacity achieving for the binary input discrete memoryless channels (B-DMCs) based on the polarization phenomenon. Letdenote the symmetric capacity of a B-DMC W. When the number of synthesized channels N is large enough, approximatesubchannels are completely noisy and the rest are noiseless by performing channel combining and splitting. The noiseless channels can be used for information transmission while the noisy ones can only be used to transmit frozen bits which are known by the transceiver. In[4], the successive cancellation (SC) decoding algorithm is proposed with a computation complexity ofIn addition to this,some enhanced decoding techniques, i.e.,the SC list (SCL) decoding [5], the SC stack(SCS) [6] and the cyclic redundant check(CRC) aided SCL (CASCL) decoding [7] algorithms are proposed to further improve the performance for a finite code length.
Recently, the multilevel coding (MLC) and bit-interleaved coded modulation (BICM)techniques are respectively combined with polar codes to improve the spectral efficiency in the practical system, which is referred as the polar coded modulation [8]. Moreover, the in-fluence of the bit mapping on the polarization effect of the quadrature amplitude modulation(QAM) constellations is explained detailedly in the polar coded modulation [8]. An efficient recursive search algorithm is proposed in [9]to find the optimal mapping for the QAM constellations in the MLC scheme. A good channel mapping way in the BICM scheme with a better performance than the random mapping is proposed in [10] [11]. In addition to this,continuous phase modulation is combined with channel codes to achieve a higher spectrum efficiency [12] [13].
Based on the given Gray mapping, the authors propose the bit interleaved coded modulation polar-APSK scheme, which neglects the correlations between the bit levels by using the bit interleaver.
Compared to the QAM constellations, the amplitude phase shift keying (APSK) constellations has a satellite practical advantage due to its lower peak-to-average power ratio(PAPR) [14].The amplitude phase shift keying(APSK) constellation consists of several concentric rings associated with uniformly distributed points. For the APSK constellations whose amplitude and phase are independent of each other, the phase should carry about 1.38 bits more information than the amplitude at a high signal to noise ratio (SNR) [15],which can be regarded as the unequal error[16].The traditional Gray mapping for the APSK constellations is proposed in [17]. As it is mentioned above, the phase carries more information than the amplitude. We can derive that there exists the polarization phenomenon between the phase and the amplitude, which meets the property of the polar codes. Thus, it is essential to study the polar coded modulation based on the APSK constellations.
In the satellite communication system,APSK constellations traditionally use the Gray mapping. Based on the fixed Gray mapping,we design the bit interleaved coded modulation polar-APSK (BICM-PA). In the BICM-PA scheme, guided by the cumulative Bhattacharyya parameter (CBP) and the upper bound for the CBP (UBC), we numerate all the bit loading of the APSK constellations to search for the best one.
In reality, the bit mapping also plays an important role in the polarization effect of the APSK constellations. Thus, a unified framework, namely multilevel polar APSK coded modulation (MLCM-PA) scheme, is put forward to jointly optimize the bit mapping and the bit loading. In order to achieve an optimal solution for the problem, we adopt a two-stage optimization approach. Firstly, a novel semiset partitioning (SSP) mapping is proposed,which shows a better polarization effect than the Gray mapping measured by the second order moment of the bit channels average mutual information (BCAMI). Secondly, we can optimize the bit loading of the APSK constellations in the MLCM-PA scheme under the proposed mapping way.
The rest of this paper is organized as follows. The APSK constellations will be introduced in Section II. In Section III, we firstly introduce the proposed BICMPA. After that,the CBP is introduced to measure the polarization effect of the APSK constellations. In addition, a simplified metric named UBC is proposed to lower the computation complexity.Section IV describes the MLCM-PA scheme above all. Then we conduct a two-stage optimization approach on the bit mapping and the bit loading based on the second order moment of the BCAMI. In Section V, the simulations results over the additive white Gaussian noise(AWGN) channel are provided. Finally, Section VI concludes the paper.
In this paper, we will use calligraphic characters, such asor, to denote a set.A random variable will be represented as the uppercase letter such as X or Y. The bold capital letter, such as X or Y, will define a matrix. We use a notationto denote a-dimension vector andto denote a subvectorwhereis defined as theth element of the vector.
II. APSK CONSTELLATIONS
The APSK constellation is known to have a lower PAPR compared to the QAM constellation, and is especially well suited for nonlinear satellite channels. In this paper, we only focus on the APSK constellations.
An APSK constellation is characterized by the number of the concentric rings and the number of points in each ring. Letdenote the radius set andis defined as the phase set. Assuming that the number of points on each ring isand the number of rings iswhereAPSK constellation setcan be given by [17]
After that, we will introduce the Gray mapping for the APSK constellations. Assume the phase offsets are determined byout of m bits, and then the phase offsets can be considered as the uniformPSK. Thus, there exists the Gray mapping for thebits related to thePSK.
In the same way, it can be found that the amplitudes, which are determined by the otherbits, can be considered as the non-uniformPAM and the Gray mapping exits for thesebits. By performing the Cartesian product, the Gray mapping for theAPSK can be determined [17]. For instance, the (3,1)16-APSK with Gray mapping is shown in figure 1, where the first 3 bits are related to the phase offsets and the last 1 bit determines the amplitude, i.e.,
The bit loading for the APSK constellations is realized by assigningbits mapped intoand the otherbits mapped intorespectively. In [15], it is demonstrated that the phase should carry more information than the amplitude, i.e.,The diversity between the phase and the amplitude will change with the configuration of the bit loading.Therefore, the polarization effect of the APSK constellations is affected by the bit loading.Similar to the QAM constellations, the bit mapping also influences the polarization effect for the APSK.
III. BIT INTERLEAVED CODED MODULATION POLAR-APSK
In a BICM setup, all bit levels are treated equally and the information loss is minimized when Gray mapping is used [8]. Based the above Gray mapping, we design the BICM-PA scheme.
In this section, the block diagram of BICMPA architecture is described firstly. After that,we will introduce the CBP as well as its upper bound UBP to measure the polarization effect of the APSK constellations. Moreover, these two metrics are used to optimize the bit loading of the APSK constellation under the Gray mapping. Finally, the method to construct the polar codes in the BICM-PA scheme is given.
3.1 The BICM-PA architecture
The block diagram of BICM-PA architecture is shown in figure 2, where N denotes the length of polar codes andmodulation is adopted. At the transmitter, the bit sequencewhich consists ofinformation bits andfrozen bits, is encoded to the coded bit sequence, whereis the generator matrix of the polar encoder.
Fig. 1 (3,1)16APSK with Gray mapping
Fig. 2 The diagram of BICM-PA architecture
After that, the bit sequenceis split into m bit streamsand each stream has a length ofThe bit streams are permuted toby a predetermined channel mapping. The mapping strategy in[10] will be used in this paper for the simplest 2×2 kernel matrix. Each bit stream is random interleaved and the output sequence of ith interleaver is denoted asThen,the m bits, which are respectively selected from the m bit streamsin the same position, are taken to form an m-binary tuple, whereNext, the formertupleis mapped into the phase offsetand the lattertupleis mapped into the amplituderespectively. Then the m-binary tupleis modulated into a certain symbolunder the Gray mapping functionof the APSK constellations.
Finally, the modulated symbolsare transmitted over theinput AWGN channelwith the transition probabilities denoted asThe jth received symbol is given by
Under the BICM-PA scheme, theinput AWGN channel can be considered as m parallel bit channelsBased on the mapping way, the channel transition probability ofcan be calculated as
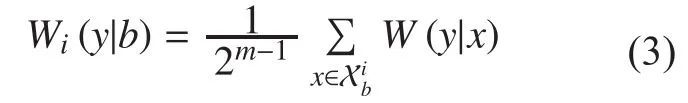
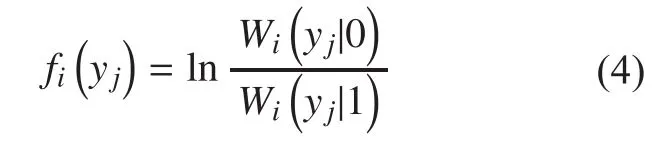
After the processing of demodulation,deinterleavers, channel demapping and parallel-to-serial permutation, these N LLRs will be sent to the decoder for an estimate of the source bit sequenceby performing SC or other enhanced decoding algorithms.

3.2 Bit loading optimization
For the given Gray mapping, the polarization effect of the APSK constellations is only relevant to the bit loading. Since the variance of the BCAMI cannot work well in the BICM scheme [8], a new metric should be proposed to measure the polarization effect of the APSK constellations in the BICM-PA scheme. In[4], Bhattacharyya parameter is used as the reliability metric of the polarized channel. Inspired by this, for the APSK constellations, we can measure the reliability of the ith parallel bit channel based on the Bhattacharyya parameter defined as
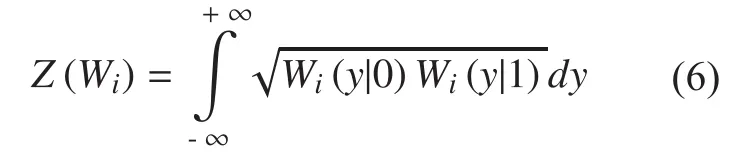
By substituting (3) into (6),can be rewritten as follows
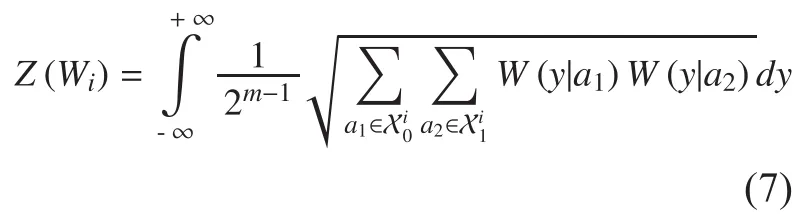
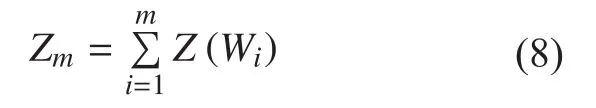
Based on the above definitions, we will numerate all the typical bit loading for 16-ary and 256-ary APSK constellations and search for the bit loading with the lowest CBP under the BICM-PA scheme.
Figure 3 gives the comparison in CBP for various APSK constellations with the Gray mapping. A higher CBP means a worse polarization effect. Under the configuration of 256APSK, the (5,3) 256APSK has the best polarization effect among these 3 pairs, while the (6,2) 256APSK has the worst polarization effect. For the 16-ary APSK constellations, the(3,1) 16APSK is better than the (2,2) 16APSK in terms of the CBP.
However, the formula (7) has a relatively high complexity because of the complex integral operation. In order to simplify the calculation, we can use the upper bound of CBP to represent it.
Lemma 1.The Bhattacharyya parameter of the ith bit channelhas the following upper bound, that is,

Proof.
Define
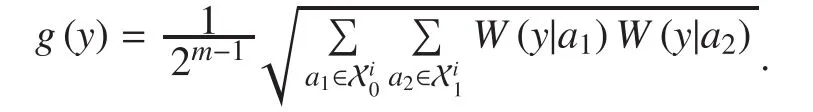
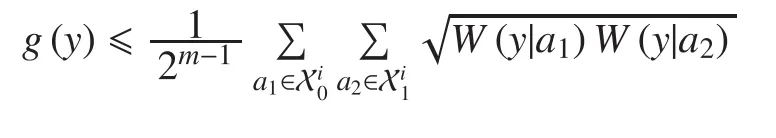

In the AWGN channel, the channel transition probability can be given by By substituting it into (10), it can be rewritten as
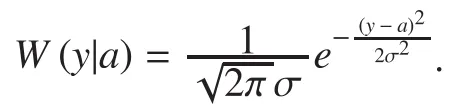
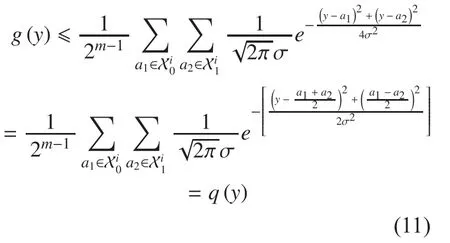
Since the integration of the Gaussian distribution, from negative infinity to positive infinity, is equal to 1, the Bhattacharyya parameter of the ith bit channelcan be written as
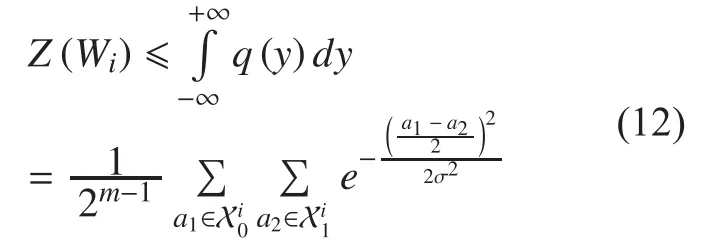
which gives the upper bound of (7).
Based on the Lemma 1, the UBC can be given by


Fig. 3 The comparison in CBP for various APSK constellations with the Gray mapping
Figure 4 gives the comparison in the CBP and the UBC for various APSK constellations with the Gray mapping. As it is shown, the UBC turns out to be the upper bound of CBP,which further demonstrates the Lemma 1. For the 256-ary APSK constellations, the (5,3)has the smallest UBC while the (6,2) has the largest one. That is, the (5,3) 256-ary APSK performs best among these 3 pairs, which is consistent with the result in figure 3. For the 16-ary APSK constellations, it also has the same conclusion. Thus, UBC can be used to measure the polarization effect of the APSK constellations while having a low computation complexity in the BICM-PA scheme.
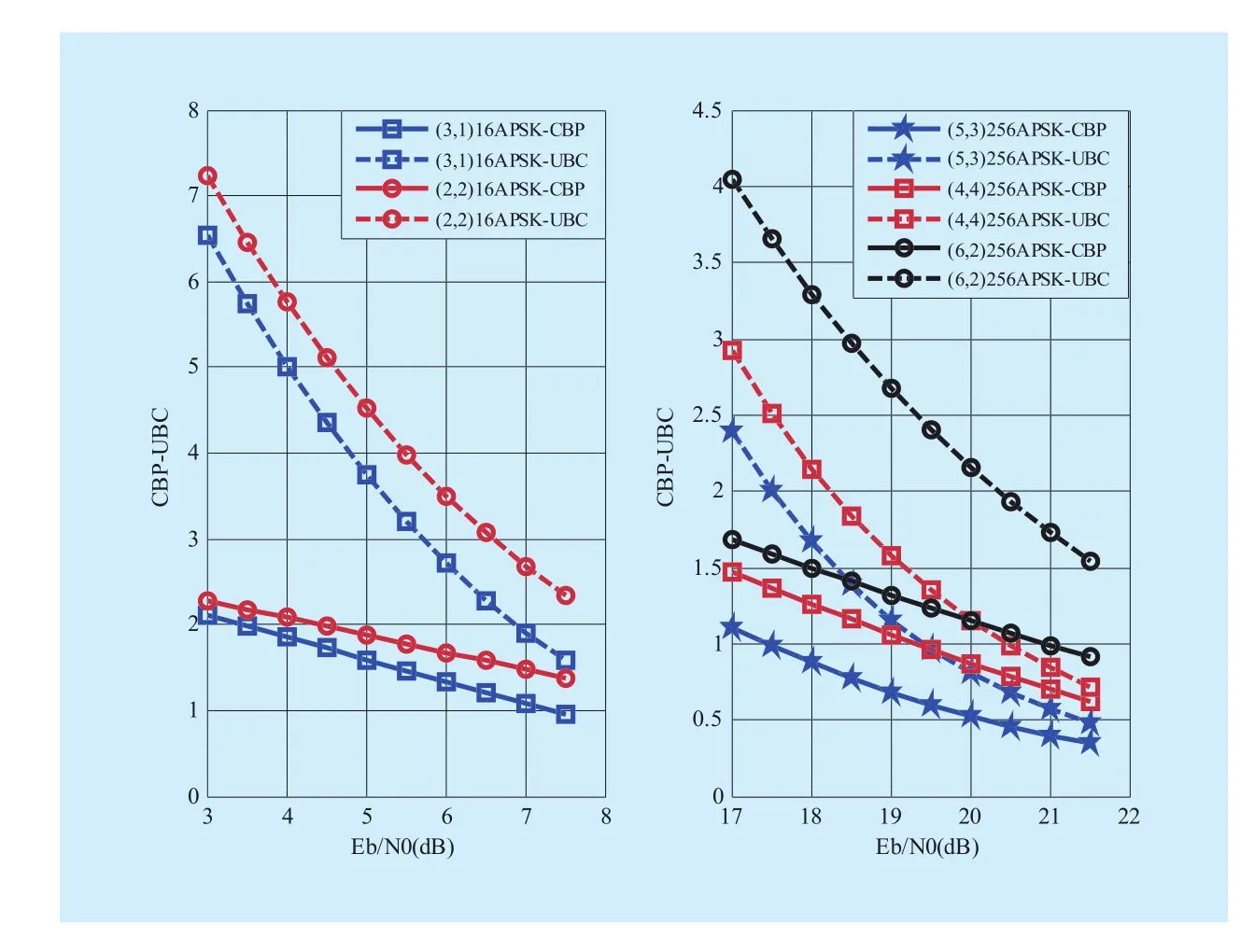
Fig. 4 The comparison in UBC for various APSK constellations with the Gray mapping
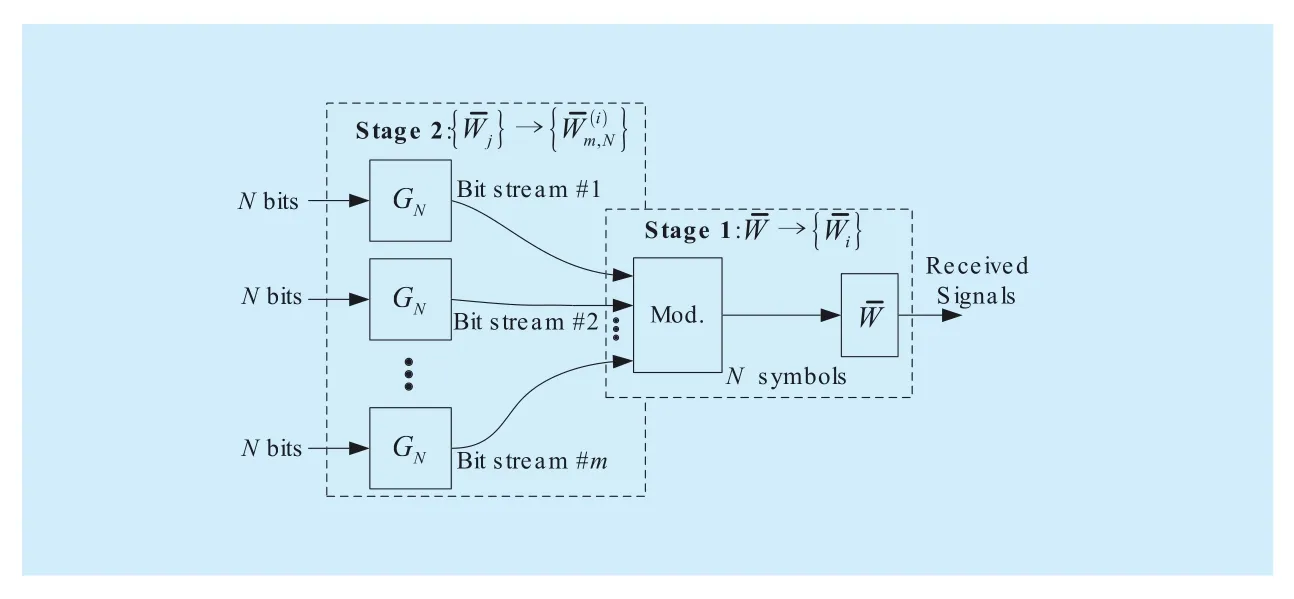
Fig. 5 The diagram of MLCM-PA architecture
3.3 Construction of polar codes in the BICM-PA scheme
The construction of polar codes is the key technique to design a BICM-PA scheme. The BICM-PA transmission scheme is constructed as follows.
Step 1) Calculate the average mutual information of the m parallel bit channels of the APSK constellation with the Gray mapping by using (14),

Step 2) Calculate the noise power of binary-input AWGN channel by using the bisection method, whose capacity is equal to that in(14).
Step 3) Gaussian approximation in [18] is performed to calculate the reliabilities of all polarized channels. The K most reliable ones,which are determined by the given rate, are selected to transmit the information bits and the others carry the frozen bits which are known to the transceiver.
The MLCM-PA transmission scheme is constructed by a two-stage channel transform. The framework of MLCM-PA is shown in figure 5.
Under the MLCM-PA scheme, theAPSK constellation input AWGN channel can be considered as m correlated bit channelsThe ML-
IV. MULTILEVEL CODED MODULATION POLAR APSK
In the above BICM-PA, only the bit loading is optimized under the fixed Gray mapping.Actually, the bit mapping also influences the polarization effect of the APSK constellations.In order to conduct a joint optimization of the bit mapping and the bit loading, we design the MLCM-PA scheme and propose the second order moment of the BCAMI as the metric to solve the optimization problem in the proposed MLCM-PA architecture.
4.1 The MLCM-PA architecture
CM-PA scheme is constructed as follows at the transmitter.
The first stage is to transform theinput channelinto m correlated bit channels. The average mutual information ofcan be calculated as follows,
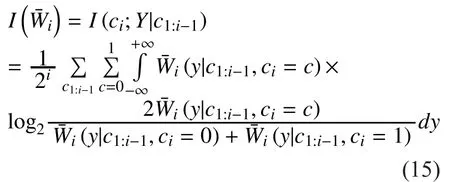
The channel transition probability ofare
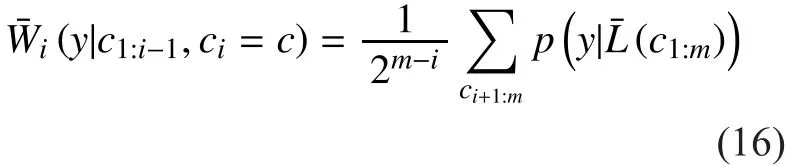
The second stage is to perform the conventional channel polarizationGaussian approximation is performed to calculate the reliabilities of all the mN B-DMCs.
Multi-stage decoding algorithm is used for the detection of MLCM-PA. At the receiver,each of the m bit-level is demodulated and decoded sequentially and each decoded bit sequence is used for the demodulation of the following bit-level. To be more specific, the input bitwise LLRs for the first polar decoders are calculated according to the received signalsfirstly. Then SC or other enhanced decoding algorithms can be performed to get the estimates of the source bits of the first polar codes. After that, the input bitwise LLRs for the second polar decoder can be calculated in aid of the decoding bit sequence of the first polar decoder and the second polar decoder can simultaneously work. In that way, the whole decoding process will stop until all the source bits are decoded.
4.2 Optimization of the MLCM-PA
In this subsection, we give the definition of the second order moment of BCAMI. Based on the second order moment of BCAMI, we will conduct a two-stage optimization approach for the bit mapping and the bit loading.
4.2.1 Definition of the second order moment of BCAMI
In [8], the variance of the modulated BCAMI is used to measure the polarization effect as follows,
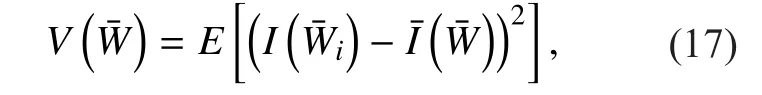
However, the variance can be only used to evaluate the performance for different mapping ways of the same signal set becauseis independent of the bit mapping and remains the same. Whilewill change along with the bit loading for the APSK constellations.Hence,should also be taken into consideration except for the variance of bit channel capacities. In that way, the new metric to measure the polarization effect for the APSK constellation can be denoted as,
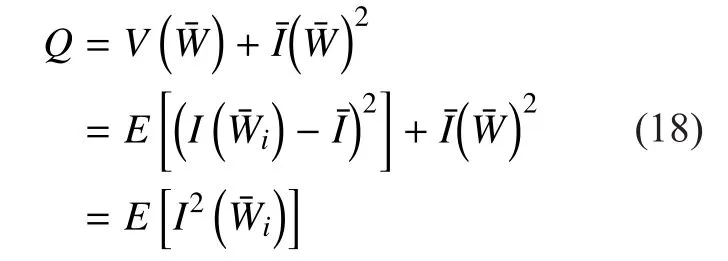
which turns out to be the second order moment of BCAMI for the m correlated bit channel.
4.2.2 Bit mapping and bit loading Optimization
It is difficult to conduct a joint optimization scheme combining the bit mapping with the bit loading in the MLCM-PA scheme. Consequently, we adopt a two-stage method.
In [8], the set-partitioning (SP) mapping is determined by partitioning signals into subsets with increasing minimum subset distances. It leads to a significantly larger bit level variance compared to the Gray mapping for the QAM constellation, thus resulting in a better performance in the MLC scheme. Nevertheless,there are few researches in how to optimize the bit mapping for the APSK constellation in the MLC scheme so far.
It can be supposed that the SP mapping maybe the best bit mapping for the APSK constellations in the MLCM-PA scheme. However, the SP mapping is hard to obtain due to the irregular structure of the APSK constellations.Accordingly, we propose the general SSP mapping described as follows.
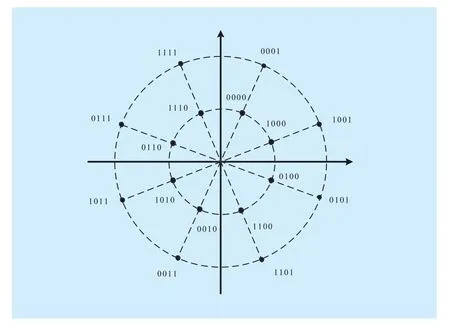
Fig. 6 (3,1) 16APSK with SSP mapping
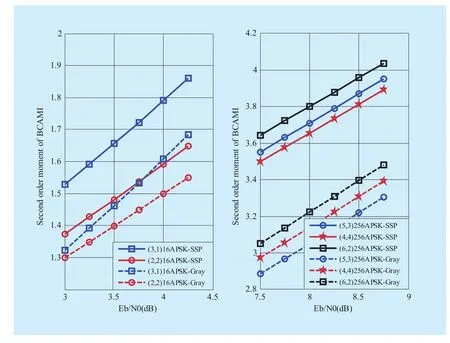
Fig. 7 The comparison in second order moment of BCAMI for various APSK constellations
Step 1) The SP mapping functionfor the phase setcan be obtained by the manner in[19].
Step 2) In the same way, the SP mapping functionexists for the amplitude set
Step 3) By performing the Cartesian product, the SSP mapping for theAPSK can be determined asIn that way, the m-tuple bit sequenceis mapped into the symbol
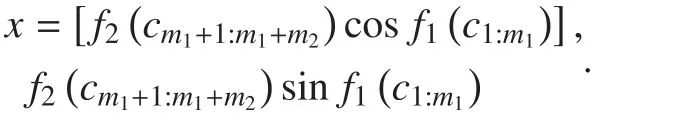
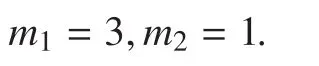
Under the SSP mapping way, we will numerate all the bit loading of 16-ary and 256-ary APSK constellations and search for the bit loading with the largest second order moment of BCAMI.
Figure 7 gives the comparison in second order moment of BCAMI for various APSK constellations with the SSP mapping as well as the Gray mapping. From figure 7, we can find that the SSP mapping has a larger second order moment of BCAMI than the Gray mapping for the same bit loading, thus having a more significant polarization effect. As a result, the SSP mapping should be preferably applied in the MLCM-PA. Given the SSP mapping, (4,4) has the smallest second order moment of BCAMI while (6,2) has the largest one for 256-ary APSK constellations. In this word, (6,2) 256-ary APSK performs best among these 3 pairs, which is different from the result in the BICM-PA architecture. For 16-ary APSK constellations, (3,1) 16APSK is still better than (2,2) 16APSK.
V. SIMULATION RESULTS
In this section, we will provide the simulation results for the BICM-PA, the MLCM-PA and the coded modulation Turbo-APSK (CM-TA)schemes [20] over the AWGN channel. In the following simulation scenes, the CA-SCL de-coding algorithm is used for the BICM-PA and the MLCM-PA schemes and the size of list is all set as 32. The CM-TA scheme adopts the LTE turbo code and Log-MPA decoding algorithm with 8 iterations. The number of transmitted symbols is defined as S and K denotes the number of information bits.
Figure 8 depicts the BLER performance for various APSK constellations with the Gray mapping in the BICM-PA architecture. Compared to the (2,2) 16APSK, the (3,1)16APSK achieves about 1dB gain. In addition, the (5,3)256APSK has the best performance for 256-ary APSK constellations while the (6,2) perform the worst. As it is shown in the previous sections, (5,3) and (3,1) are the best configurations of bit loading for 256-ary and 16-ary APSK constellations according to the CBP and UBC in the BICM-PA scheme. In a word,the CBP and UBC can be used to optimize the bit loading of the APSK constellations in the BICM-PA scheme.
Figure 9 gives the simulation results for 16APSK and 256APSK of different parameters. It is shown that the APSK constellations with the SSP mapping all perform better than that with the Gray mapping based on the same bit loading. Given the SSP mapping, the(3,1) 16APSK performs better than the (2,2)16APSK. From the simulation results, the(6,2) 256APSK performs best and the (4,4)256APSK has the worst performance. Identically, the (6,2) 256APSK and (3,1) 16APSK are respectively the best configurations of the bit loading in view of the second order moment of BCAMI for the MLCM-PA scheme.
As shown in figure 9, the (3,1) 16APSK with the Gray mapping has a better BLER performance than the (2,2) 16APSK with the SSP mapping. In figure 7, it is shown that the (3,1)16APSK with the Gray mapping has a lower second order moment of BCAMI than the(2,2) 16APSK with the SSP mapping in the low SNR region. The reason why the BLER performance is not in agreement with the analyses in the low SNR region is that there may exist a slight mismatch between the polar codes and APSK constellations. While, the(3,1) 16APSK with the Gray mapping still has a larger second order moment of BCAMI than the (2,2) 16APSK with the SSP mapping in a relatively high SNR region, which illustrates that the proposed metric can approximately measure the polarization effect of the APSK constellations.
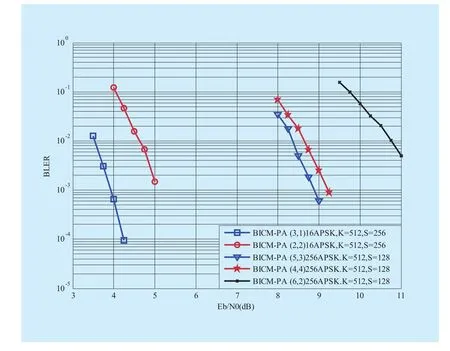
Fig. 8 The simulation results for various APSK constellations with the Gray mapping in the BICM-PA architecture
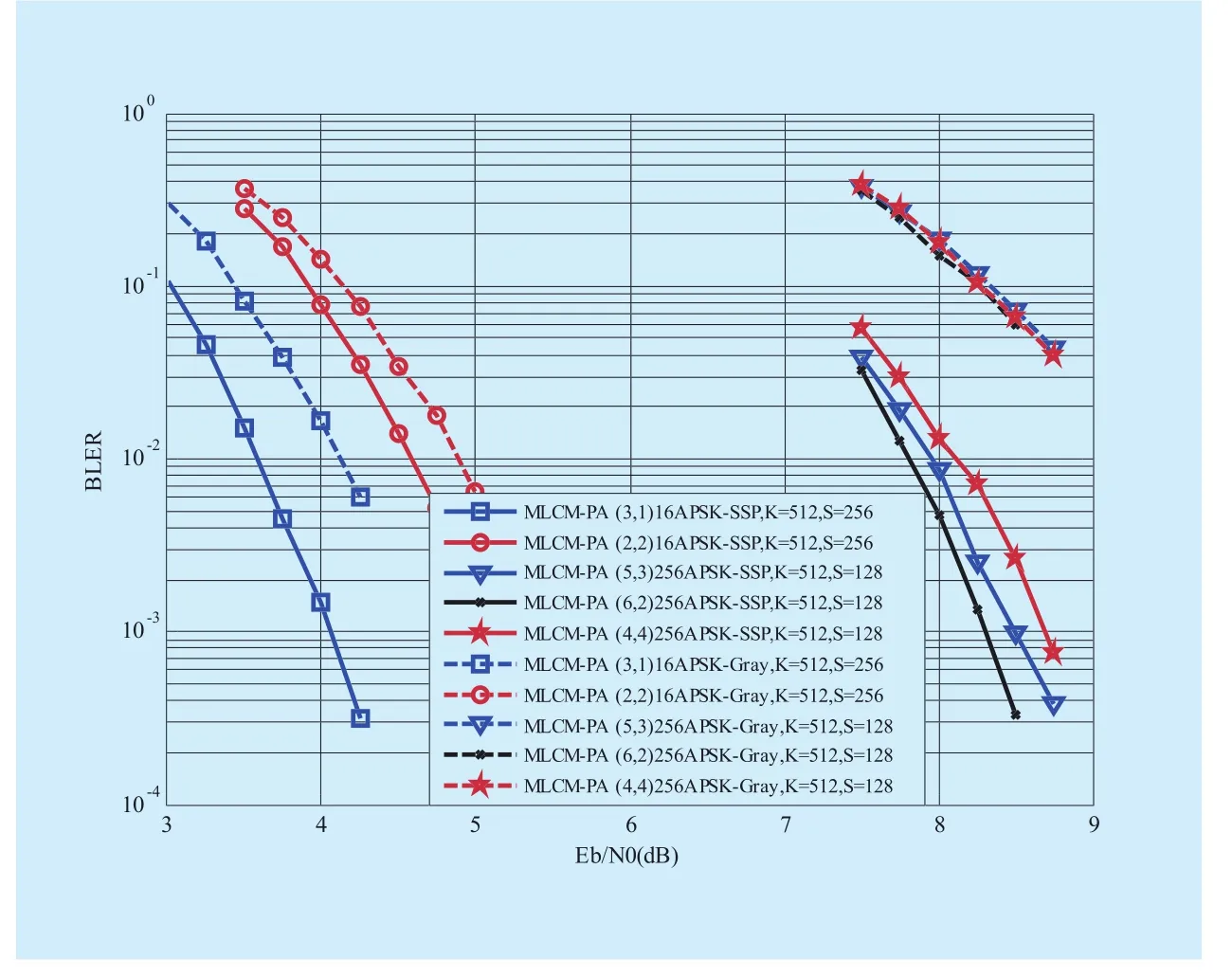
Fig. 9 The simulation results for various APSK constellations in MLCM-PA architecture
1 The SP mapping for(3,1) 16APSK is designed to maximize the minimum Euclidean distance of the subsets by hand when conducting the set partitioning operations.
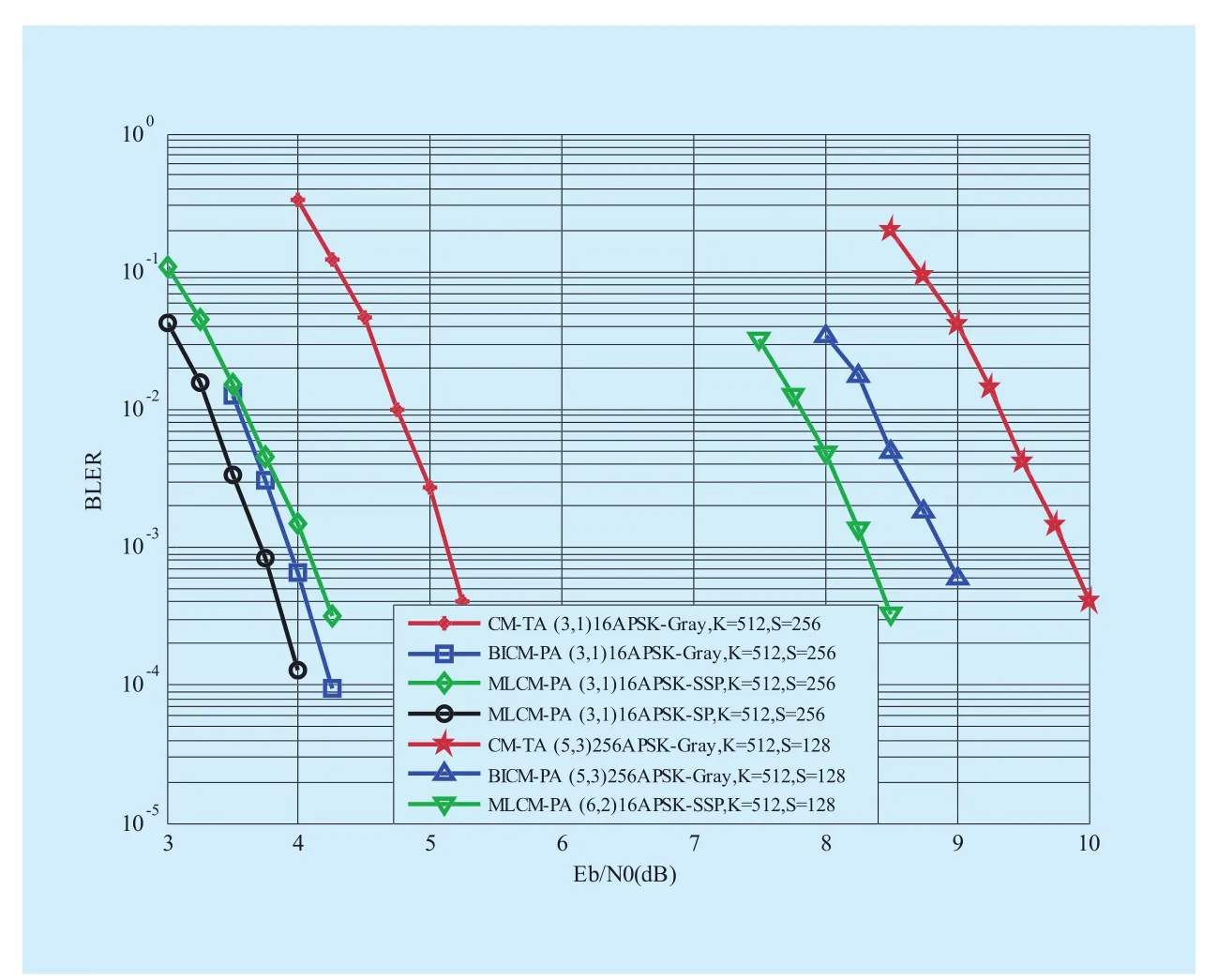
Fig. 10 The comparison in BLER for CM-TA, BICM-PA and MLCM-PA
In a word, the second order moment of BCAMI can be used to optimize the bit mapping and bit loading of the APSK constellations in the MLCM-PA scheme.
The BLER comparison for the CM-TA, the BICM-PA and the MLCM-PA is shown in figure 10. The configurations of the bit loading of the 16APSK and 256APSK take the optimal values in section III for the CM-TA schemes.From the simulation results, it is found that over 1dB gain can be achieved for the BICMPA and the MLCM-PA compared to the CMTA schemes.
It is found that the MLCM-PA (3,1)16APSK with the SP mapping1can achieve about 0.25 dB gain compared to the BICMPA (3,1) 16APSK. However, this SP mapping is designed by hand and hard to obtain for the high-dimension constellations because of the irregular structure of the APSK constellations.On the other hand, the proposed SSP mapping is a universal scheme for arbitrary APSK constellations with a slight performance loss.
Moreover, the MLCM-PA can provide nearly 0.5dB gain more than the BICM-PA for the 256APSK constellations, which can verify the effectiveness of the proposed SSP mapping for APSK constellations.
VI. CONCLUSIONS
In this paper, we conduct a research on the polar coded modulation based on the APSK constellations. For the proposed BICM-PA scheme, a new metric called CBP is introduced to measure the polarization effect of the APSK constellations. In addition, the UBC is proposed to represent the CBP while having a lower computation complexity. Moreover,the CBP and UBC are used to optimize the bit loading of APSK constellations in the BICMPA architecture. For the MLCM-PA scheme,we use the second order moment of BCAMI as the metric to measure the polarization effect of the APSK constellations. Based on the second order moment of BCAMI, a two-stage optimization approach is conducted to optimize the bit mapping and bit loading. Simulation results demonstrate the validity of all the metrics for these two transmission schemes respectively. Besides, the BICM-PA and the MLCM-PA schemes both outperform the CMTA scheme by up to more than 1dB.
ACKNOWLEDGEMENTS
This work is supported by the National Natural Science Foundation of China (No. 61171099,No.61671080), Nokia Beijing Bell lab.
[1] I. Hussain, M. Xiao and L. Rasmussen, “Erasure Floor Analysis of Distributed LT Codes”, IEEE Transactions on Communications, vol. 63, No. 8,pp. 2788-2796, August 2015.
[2] I. Hussain, M. Xiao and L. Rasmussen, “Buffer-based Distributed LT Codes”, IEEE Transactions on Communications, vol. 62, no. 11, pp.3725-3739, November, 2014.
[3] I. Hussain, M. Xiao and L. K. Rasmussen, “Rateless Codes for the Multiway Relay Channel,” in IEEE Wireless Communications Letters, vol. 3, no.5, pp. 457-460, Oct. 2014.
[4] E. Arikan, Channel polarization, “A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels”, IEEE Transactions on Information Theory, vol. 55, no.7, pp. 3051-3073, July 2009.
[5] I. Tal and A. Vardy, “List Decoding of Polar Codes”, IEEE Transactions on Information Theory, vol. 61, no. 5, pp. 2213-2226, May 2015.
[6] K. Niu and K. Chen, “Stack decoding of polar codes”, Electronics Letters, vol. 48, no. 12, pp.695-696, 2012.
[7] K. Niu and K. Chen, “CRC-aided decoding of polar codes”, IEEE Commun. Letters, vol. 16, no.10, pp. 1668-1671, 2012.
[8] M. Seidl, A. Schenk, C. Stierstorfer, and J.B.Huber, “Polar-Coded Modulation”, IEEE Transactions on Communications, vol. 61, no. 10,pp.4108-4119, October 2013.
[9] K. Chen, K. Niu, and J. R. Lin, “Polar coded modulation with optimal constellation labeling”, in National Doctoral Academic Forum on Information and Communications Technology, pp.1-5,21-23 Aug. 2013.
[10] K. Chen, K. Niu, and J. R. Lin, “An efficient design of bit-interleaved polar coded modulation”, in IEEE 24th International Symposium on Personal Indoor and Mobile Radio Communications (PIMRC), pp.693-697, 8-11 Sept. 2013.
[11] D. M. Shin, S. C. Lim, and K. Yang, “Mapping Selection and Code Construction for 2m-ary Polar-Coded Modulation”, IEEE Commun. Letters,vol. 16, no. 6, pp. 905-908, 2012.
[12] M. Xiao and T. Aulin, “On Analysis and Design of Low Density Generator Matrix Codes for Continuous Phase Modulation,” IEEE Transactions on Wireless Communications, September,2007, pp. 3440-3449.
[13] M. Xiao and T. Aulin, “Serially Concatenated Continuous Phase Modulation with Ring Convolution Codes,” IEEE Transactions on Communications, August 2006, pp. 1387-1396.
[14] R. D. Gaudenzi, A. Guillen, and A. Martinez,“Performance analysis of turbo-coded APSK modulations over nonlinear satellite channels”,IEEE Transactions on Wireless Communications,vol. 5, no. 6, pp. 2396-2407, September 2006.
[15] Q. Xie, Z. Wang and Z. Yang, “Polar Decomposition of Mutual Information Over Complex-Valued Channels”, IEEE Transactions on Information Theory, vol. 60, no. 6, pp. 3163-3171, June 2014.
[16] J. Huang; Z. Fei; C. Cao; M. Xiao; D. Jia, “On-line Fountain Codes with Unequal Error Protection,”IEEE Communications Letters , vol.PP, no.99,pp.1-1
[17] Z. Liu, Q. Xie, and K. Peng et al., “APSK constellation with Gray mapping”, IEEE Commun. Letters,vol. 15, no. 12, pp. 1271-1273, Dec. 2011.
[18] P. Trifonov, “Efficient Design and Decoding of Polar Codes”, IEEE Transactions on Communications, vol.60, no.11, pp. 3221-3227, Nov. 2012.
[19] G. Ungerboeck, “Treliss-Coded modulation with redundant signal sets- part I:introduction”, IEEE Communi. Mag., vol. 25, no. 2, pp.5-11,Feb.1987.
[20] 3GPP TS 25.212, Multiplexing and channel coding (FDD), Release 9, 2009.
- China Communications的其它文章
- An Iterative Detection/Decoding Algorithm of Correlated Sources for the LDPC-Based Relay Systems
- Homomorphic Error-Control Codes for Linear Network Coding in Packet Networks
- A Privacy-Based SLA Violation Detection Model for the Security of Cloud Computing
- An Aware-Scheduling Security Architecture with Priority-Equal Multi-Controller for SDN
- A Flow-Based Authentication Handover Mechanism for Multi-Domain SDN Mobility Environment
- Light Weight Cryptographic Address Generation (LWCGA) Using System State Entropy Gathering for IPv6 Based MANETs

