Generalized Block Markov Superposition Transmission over Free-Space Optical Links

Jinshun Zhu, Shancheng Zhao, Xiao Ma

1 School of Electronics and Information Technology, Sun Yat-sen University, Guangzhou 510006, China

2 College of Information Science and Technology, Jinan University, Guangzhou 510632, China

3 School of Data and Computer Science, Sun Yat-sen University, Guangzhou 510006, China

4 Guangdong Key Laboratory of Information Security Technology, Sun Yat-sen University, Guangzhou 510006, China

* The corresponding author, email: maxiao@mail. sysu.edu.cn

I. INTRODUCTION

Free-space optical (FSO) communications,which have attracted considerable attention recently, offer significant advantages such as high bandwidth capacity, unregulated spectrum, inherent security, fast deployment, and so on [1]. With these virtues, FSO communication systems are appealing for a number of applications and markets, including last mile connectivity, optical fiber backup, satellite communications [2,3].

In FSO communications, optical transceivers communicate over point-to-point lineof-sight links. The performance of the FSO communication system is affected by the misalignment-induced pointing errors and weather conditions. Even under clear sky conditions, performance of the FSO communication system is severely degraded by atmospheric turbulence [4]. Turbulence is a natural phenomenon caused by inhomogeneities in temperature and pressure of the atmosphere,which leads to the refractive index variations along the transmission paths. The atmospher-ic turbulence produces random fluctuations in both amplitude and phase of the received signal, i.e., channel fading. The adverse effect of turbulence is more significant over link distances of several kilometers [4]. In this paper,we assume that the transceivers are perfectly aligned and do not consider the pointing errors. We also assume that the communication system is under clear sky conditions, and focus on mitigating the channel fading caused by atmospheric turbulence.

In this paper, the authors have presented a generalized block Markov superposition transmission (GBMST)to combat the channel fading induced by atmospheric turbulence.

In order to improve the reliability over atmospheric turbulence channels, the FSO communication system can employ mitigation techniques such as channel coding techniques[5-8], diversity techniques [5-17], adaptive transmission [18,19], relay-assisted transmission [20,21], hybrid RF/FSO [22,23], and so on. Due to their good performance and easy implementation, channel coding and diversity techniques are commonly used in FSO links.Channel coding is efficient under weak turbulence conditions and is also useful under moderate and strong turbulence conditions when combined with diversity techniques [5-7]. Generally, diversity techniques can be realized in space, wavelength or time domain.In spatial diversity schemes, an FSO system employs multiple emitters at the transmitter and/or multiple apertures at the receiver, receiving multiple copies of the same signal[9,10]. Aperture averaging can also be viewed as a simple spatial diversity technique, where the receiver lens aperture is larger than the fading correlation length [7]. For the case of wavelength diversity [11,12], the same signal is sent at different wavelengths with a composite transmitter, and each copy is detected by corresponding wavelength-selected receiver. Here, we consider the system with a monochromatic emitter at the transmitter and a single aperture at the receiver. Assuming that there is no aperture averaging, then the only possible diversity source in the system is time diversity. In [5-6], time diversity is achieved by combining channel coding and interleaving. In [13-17], delay-based time diversity techniques are employed, where the original signal and its time-delayed versions are sent at different fading durations and contaminated by different channel fades. An error-correcting code is said to have full diversity, if diversity order the code achieved (i.e., the slope of the error-rate curve in log-log scale) is equal to the number of different channel fades a codeword experienced. In time-delay based diversity techniques [13-17], the same signal is sent multiple times, and this is referred to as repetition coding (RC). Full time diversity can be simply achieved by repetition coding.However, such a scheme suffers from severe reduction of transmission rate as the diversity order increases [13-17].

In this paper, we propose to use block Markov superposition transmission (BMST) [24]to construct schemes with improved diversity gain over FSO links, but with only slight rate reduction. BMST is effective in constructing capacity-approaching coding schemes for additive white Gaussian noise (AWGN) channels. To the best knowledge of the authors,its application in FSO links has never been investigated in the literature. In the BMST scheme, binary sequences are encoded with a basic code and then transmitted multiple times(in their interleaved versions) to improve the transmission reliability. Meanwhile, the interleaved sequences are superimposed in a block Markov manner to maintain the transmission efficiency. The Markov superposition solves the rate reduction problem induced by repetition, but introduces interference among the consecutive transmissions. In AWGN channels, the effect of interference can be eliminated using a sliding-window decoding algorithm at the receiver [24]. However, over atmospheric turbulence channels, deep fades may lead to severe error propagation in recovery process and hence severely degrades the error performance. Hence, it needs further effort to investigate the application of BMST over atmospheric turbulence channels.

Compared with original BMST scheme,systematic BMST scheme is more effective to combat the effect of error propagation [25].The systematic bits in the systematic BMST scheme improve the resistance to error propagation, however, which need to be strengthened further under moderate and strong turbulence conditions. In this paper, we present a generalized BMST (GBMST) scheme, which can be viewed as a unified description (but not limited to) of the original BMST and the systematic BMST. In the GBMST scheme,each information sequence is repeated multiple times. Different from the original BMST and the systematic BMST, in GBMST, each replica is transmitted with a possibly different transmission memory. Based on analyzing an equivalent system, a lower bound on the bit-error-rate (BER) of the proposed scheme is presented. Extensive simulations are performed to investigate the performance of GBMST scheme over FSO links, which show that: Firstly, under a wide range of turbulence conditions, the proposed scheme improves diversity gain with only a slight reduction of transmission rate. Secondly, GBMST systems with appropriate settings can approach the derived lower bound, implying that full diversity is achievable. Thirdly, to achieve high diversity order under moderate or strong turbulence conditions, more systematic transmission is required. We also compare the error performance of the GBMST scheme with a scheme based on low-density parity-check (LDPC)codes over moderate turbulence conditions.The comparison results confirm the performance advantages of the GBMST scheme.

II. CHANNEL MODEL

To characterize atmospheric turbulence induced fading over the FSO links, several statistical models are employed [4,10,26-28].The log-normal model is widely used under weak turbulence conditions [4,26]. The K-distribution model fits well the strong turbulence conditions [4,10]. The gamma-gamma model can suitably describe the irradiance fluctuation in a wide range of turbulence regimes (from weak to strong) [4,27]. In this paper, we adopt the gamma-gamma distribution to model the fading statistics of the channel. By the gamma-gamma model, the received intensity I is defined as the product of two statistically independent random variables Ixand Iy, which arise from large-scale and small-scale turbulent eddies, respectively. The probability density function (PDF) of the normalized intensity I =IxIyis given by [4,27],

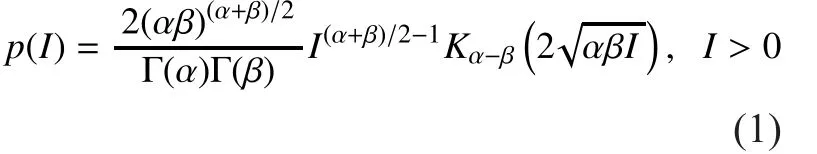
where α and β are the effective number of large-scale and small-scale eddies, respectively, Ka(·) is the modified Bessel function of the second kind of order a, and Γ(·) is the gamma function. Assuming plane wave propagation,the two parameters α and β are directly related to atmospheric conditions according to [4,27],

The correlation time of the channel fading induced by atmospheric turbulence is typically a few milliseconds, which is much greater than single symbol duration in FSO systems [29].Therefore, we consider the channel temporally varies according to the theoretical quasi-static(frozen) model [5,6,13-17], where the channel fading remains constant over the duration of consecutive symbols within a block and is independent and identically distributed (i.i.d.)across different blocks. In [30-32], channel capacities and error performances of the coded FSO systems are analyzed based on the assumption that temporal correlation is overcome with extremely long interleavers and the channel fading corresponding to each symbol is i.i.d. In this paper, following [5,6,13-17], we assume that the interleaving depth is finite and the transmission can benefit from some degree of time diversity. To obtain a target degree of time diversity of D, perfect interleaving can be achieved by simply transmitting the same information data D times with different time delays, corrupted by different channel fades[14-17]. We also assume that channel state information (CSI) is perfectly known at the receiver, which is normally achievable for FSO systems due to the slow variation of channel fading.

The typical method to enhance reliability is transmitting the same data multiple times over different fading blocks, i.e., repetition coding[11-17]. More complicated coding schemes can be found in [5,6,8]. We consider transmission of coded sequences with length Ncover atmospheric turbulence channels. A coded sequence is divided into F sub-blocks of length Nf= Nc/F each, and these sub-blocks are affected by independent channel fades. In this paper, we consider intensity modulation with direct detection (IM/DD), which is used in most current optical communication systems.We also consider the most commonly used intensity modulation technique, the on-off keying (OOK) modulation. When a modulated symbol xjis transmitted, the received electrical signal after the optical/electrical conversion is

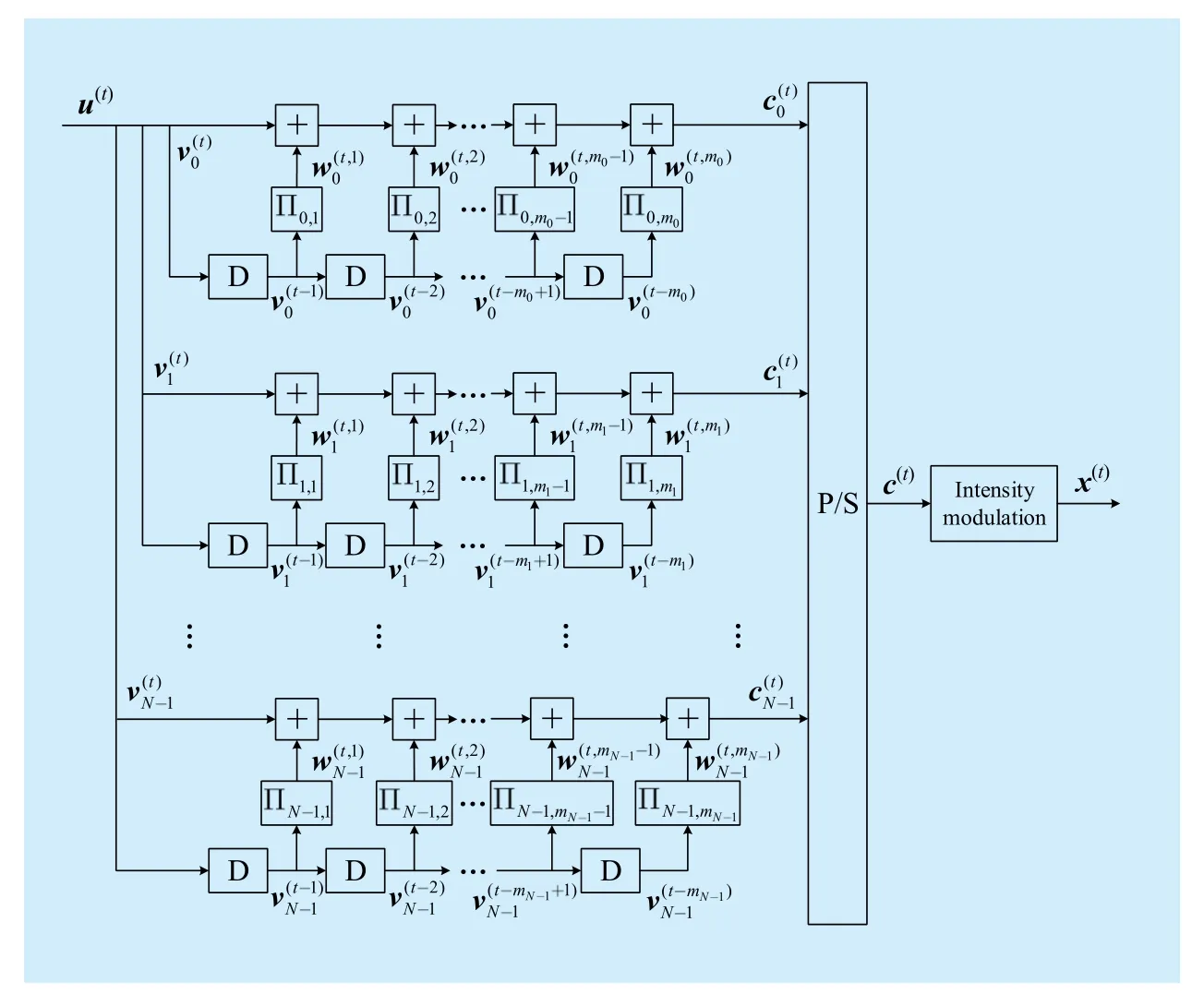
Fig. 1 Encoding/modulation diagram of the GBMST system with repetition degree N and memory sequence

III. GENERALIZED BLOCK MARKOV SUPERPOSITION TRANSMISSION OVER FSO LINKS

3.1 Encoding/modulation algorithm at transmitter

in N replicas. Then, each replica and its interleaved versions are transmitted in a block Markov superposition manner, with a possibly different memory. We denote the memories by a sequenceThe sum of the memories is denoted byand the maximum component in m is denoted byThe encoding/modulation algorithm for the GBMST system with memory sequenceis described as follows (see figure 1 for reference), where the interleaversare of size K.

Algorithm 1:The Encoding/modulation Algorithm of GBMST System

● Initialization:Forandset

● Recursion:For

4) Modulation: Map the coded sequenceinto a signal sequence x(t)using intensity modulation, and take x(t)as the transmission sequence.

InAlgorithm 1,the operation of superposition is overThe termination of the transmission can be done easily with a zero-tail after L data blocks. That is, forwe setcompute c(t)following the steps inRecursion in Algorithm 1,and then take x(t)corresponding to the redundant check part of c(t)as the t-th block of transmission. L is called the termination length. For each sub-block,redundant bits are transmitted for termination. The transmission rate of the terminated GBMST system is

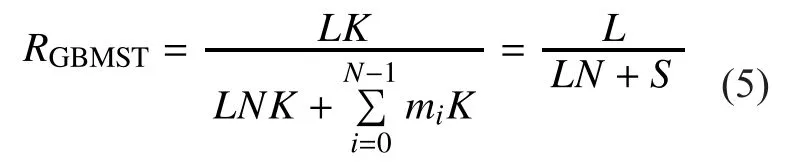
which is less than that of the basic RC code due to termination. However, when L is large enough, the rate loss caused by termination is negligible. For each information sequence u(t), there arereplicas transmitted at time t and niinterleaved versions transmitted at timeforwhere niis the number of components larger thanThe corresponding sequence is denoted byFor examplecorresponds toandcorresponds to

Remarks:The original BMST scheme [24]with memory a can be viewed as a GBMST scheme withforif each interleaver of size NK in the original scheme is composed of N sub-interleavers of size K. The systematic BMST scheme [25] with memory a can be viewed as a GBMST scheme with m0= 0 and

3.2 Transmission over FSO links

The modulated sequence x(t)is transmitted over atmospheric turbulence channels, and the received electrical signal after the optical/electrical conversion is

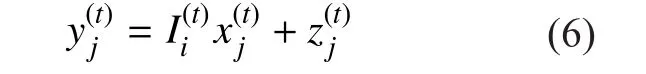
3.3 Detection/decoding algorithm at receiver

The detection/decoding algorithm at receiver can be described as an iterative message processing/passing algorithm over the associated normal graph [33]. In the normal graph, edges represent variables and vertices (nodes) represent constraints. All edges connected to a node must satisfy the specific constraint of the node.Figure 3 shows the normal graph of a GBMST system with L = 3, N = 3, andThere are four types of nodes in the normal graph of the GBMST system.

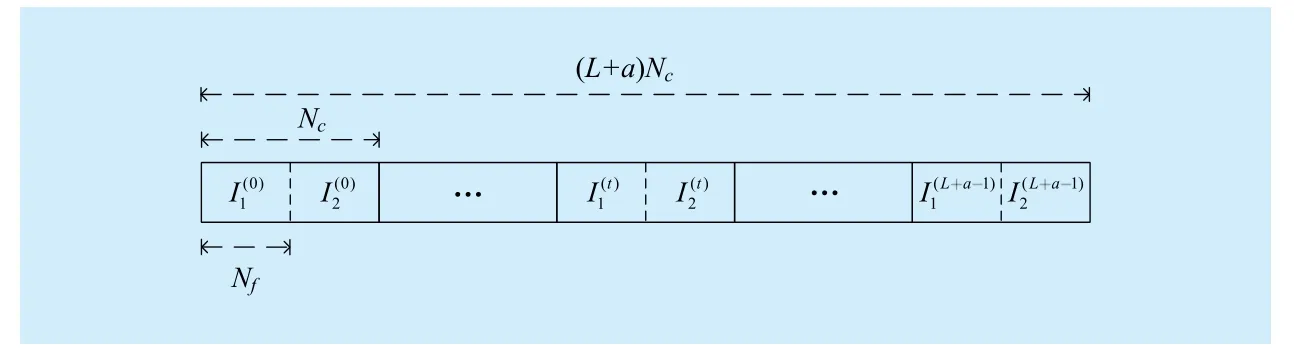
Fig. 2 Illustration of block-fading channel with F = 2 for the GBMST system with termination length L and memory sequence m = (a, a). The length of each RC-coded sequence is Nc

The iterative sliding-window detection/decoding algorithm is described as follows.

Algorithm 2:Iterative Sliding-window Detection /decoding Algorithm

● Global Initialization:Assume thathave been received. Compute

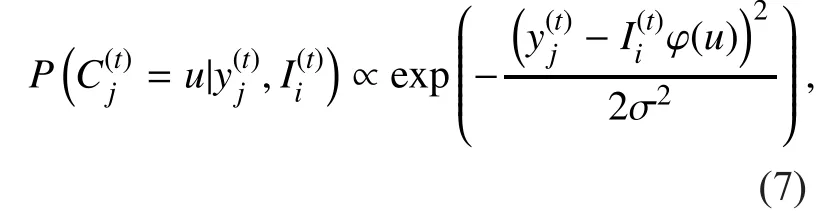
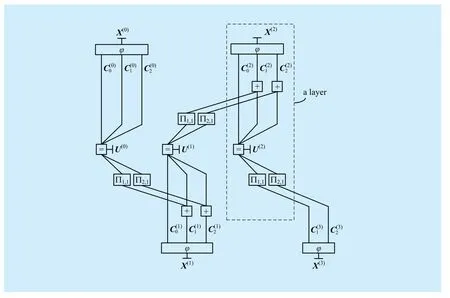
Fig. 3 Normal graph for a GBMST system with L = 3, N = 3, and m = (0, 1, 1)

● Sliding-window decoding:For t = 0,1,2,..., L−1,

a) Parallel Processes: Perform a message processing/passing algorithm employing the parallel (flooding) updating schedule. For all the layers within the window, the algorithm is scheduled as:

b) Hard decision: Make hard decisions onresulting inEstimate the entropy rateof[24]. Outputand exit the iteration, if

3) Cancelation: Remove the effect ofon all layers by updating the a posteriori probabilities associated

3.4 Decoding complexity

The decoding complexity can be analyzed from the normal graph. Let Opt(A) denote the number of operations at a generic node A.Each decoding layer actually has K parallel nodesof degree N + S. Each decoding layer also has K parallel nodesof degreeparallel nodesof degreethe computational complexity of the nodein each layer is equal to that of K parallel nodesof degree N + S. The total number of operations for each decoding layer at each iteration is then given bySince both the nodeand the nodehave computational complexity, the decoding complexity at each decoding layer at each iteration is O(2K(N + S)). To recover a target layer with a decoding delay d, the adjacent d + 1 layers are involved. Hence the total decoding complexity at each iteration is given by O(2K(N + S)(d + 1)). Finally, we need to point out that the decoding complexity also relies on the iteration numbers. In our simulations, we find that it requires (in the low BER region) 3 ～ 5 iterations on average to decode one layer with a properly designed stopping criterion.

IV. GENIE-AIDED LOWER BOUND

In the GBMST system, a single data block is involved in M + 1 consecutive transmissions by Markov superposition. The superposition introduces interference among adjacent data blocks and possible error propagation in the process of data recovery. Similar to the analysis in [24], the bit-error-rate (BER) performance of the GBMST system can be lower-bounded by a genie-aided decoder in which all but one data blocks are known. That is, with knowledge of CSI, the genie-aided decoder computesfor allandwith the dataavailable. We introduce an equivalent system for the genie-aided decoder as depicted in figure 4, corresponding to the case that the components in m are arranged in a descending order. The process for the equivalent system is described as follows. At time t, repeattimes such thatforand then obtain a binary sequenceThe sequenceis modulated into a signal sequenceand is transmitted over atmospheric turbulence channels. Forandinterleaved replicas are transmitted. Foris corresponding toin the GBMST system. Forandis corresponding toin the GBMST system.

In the equivalent system, each symbol is transmitted independently without interference. Hence, without loss of generality,we setto simplify the analysis. The information bit is repeatedtimes, resulting in a binary sequenceThe sequencecan been viewed as a codeword of a repetition code with informationand codeword lengthThe coded sequence is modulated into a signal sequenceand transmitted over atmospheric turbulence channels. The corresponding fading coefficients arewhereandforThe conditional error probability with respect to fading coefficientsis given by [34]

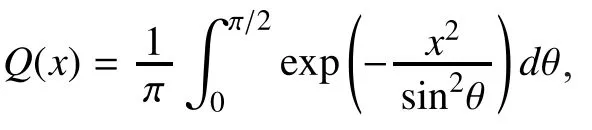
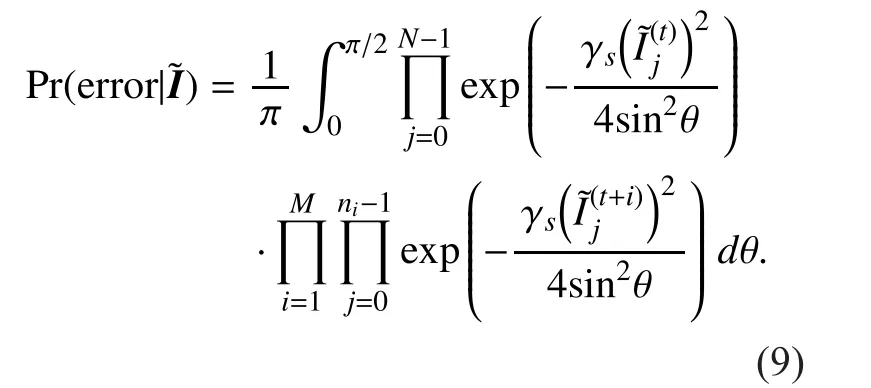
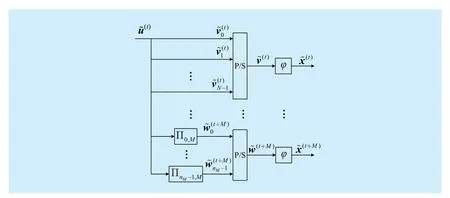
Fig. 4 Equivalent system corresponding to the genie-aided decoder for the GBMST system with repetition degree N and memory sequence m

In this paper, gamma-gamma channel mod-el is adopted. Here, we only consider two cases that F = 1 and F = N. For the case F = 1, the components in eachremain a constant value and change independently to a new value when i varies. The symbols inexperienceindependent channel fades,and hence the equivalent system can achieve diversity order of. The average ofwith respect tocan be obtained as

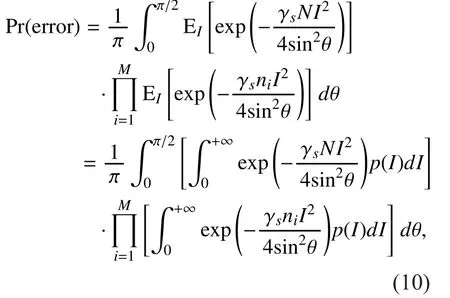
where E(·) is the expectation operation. For the casethesymbols inexperiencesindependent channel fades, and the equivalent system can obtain full diversity order. The average ofwith respect tocan be obtained as

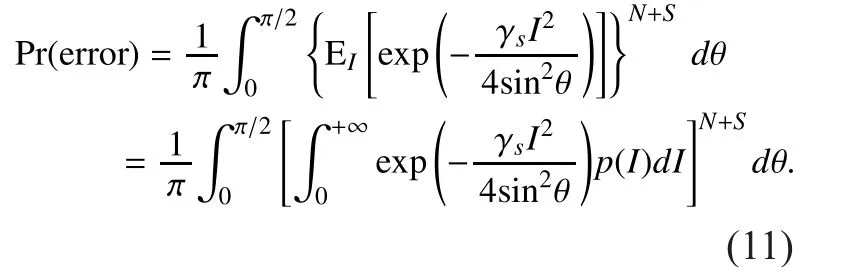
In this paper, the mean SNR per symbol is defined asand the mean SNR per information bit is given bywhere R is the transmission rate. Letandbe the BER performance functions of the equivalent system and the GBMST system, respectively, where pbis the BER andis in dB. With a similar argument given in [24], taking into account the rate loss,the BER performance of the GBMST systemcan be lower-bounded as

If a GBMST system can eliminate the effect of interference and approaches its lower bound, the system also achieves diversity order of M + 1 when F = 1 and diversity order of N + S when F = N.

1) Initialize the repetition degree N = 2.

2) Set the sum of the memoriesand generate S interleavers randomly.

3) Calculate the lower bound of the BER performance of the GBMST system according to equation (12).

4) Find a GBMST system with memory sequencesatisfyingto approach the lower bound. If there is no such a GBMST system,set N = N + 1 and go to the Step 2).

In next section, we will see that the GBMST systems with memory sequence m = (0, S) are more robust to the error propagation comparing with its counterparts and multiple transmission of systematic bits can help improve the resistance to error propagation. Hence, Step 4) in above procedure can be easily implemented. The above construction procedure can also be generalized to the case F = 1.

V. NUMERICAL RESULTS

In this section, we present several examples to investigate the performance of GBMST scheme under weak, moderate,and strong turbulence conditions. We setfor the cases of weak,moderate and, strong turbulence conditions,respectively. The interleavers used in the systems are randomly generated but fixed. The iterative sliding-window detection/decoding algorithm performs with a maximum iteration number of 18, and the entropy stopping criterion is employed with a preselected thresholdUnless stated otherwise, in our sim-ulations, the termination length is L = 50 and the information length is K = 100.

5.1 Weak turbulence conditions

For the weak turbulence conditions, we setwhich results inand

Example 1:In this example, we set repetition degree N = 2 and decoding delay d = 2S.The considered memory sequences include m = (1, 1), (1, 3), (2, 2), (0, 4), (4, 4), and(0, 8). For S = 2, 4, and 8, the corresponding transmission rates are 0.4902, 0.4808, and 0.4630, respectively. The independent transmission with repetition code of rate 0.5 can be viewed as a GBMST system with m = (0, 0).The error performance of the GBMST systems when F = 2 is shown in figure 5. We have the following observations.

1) Due to the error propagation, the iterative sliding-window detection/decoding algorithm cannot work well in the low SNR region. It is obvious that, for a GBMST system with memory sequence m in the form ofa larger a will lead to severer error propagation.This is the reason that the GBMST system performs even worse as a increases in the low SNR region.

2) The GBMST system without systematic bits can approach the lower bound only when the memory sequence m = (1, 1), and cannot mitigate the error propagation efficiently when S becomes large.

3) Compared with their counterparts with m = (2, 2)(or (1, 3)) and m = (4, 4),the GBMST systems with m = (0, 4) and m = (0, 8) mitigate the error propagation effi-ciently and approach the corresponding lower bounds in the high SNR region. This result indicates that systematic bits are preferred for GBMST to achieve higher diversity and full diversity is achieved by GBMST systems with systematic bits.

4) Compared with the independent transmission with repetition code of rate 0.5,GBMST systems with S = 2, 4, and 8 (corresponding transmission rates are 0.4902,0.4808, and 0.4630) improve diversity gain with only a slight reduction of transmission rate. Especially, GBMST systems with systematic bits can achieve full diversity order of S + 2, while the diversity order achieved by the independent transmission is only 2.

From above numerical results, we find that, on one hand, the GBMST systems without systematic bits suffer from severe error propagation. The systems without systematic bits cannot mitigate the error propagation efficiently when S is large and cannot approach the corresponding lower bounds consequently.Hence, they are not suitable to obtain high diversity order over FSO links. On the other hand, systematic bits make the GBMST systems more robust against the error propagation. The GBMST systems with systematic bits can mitigate the error propagation efficiently and hence approach the corresponding lower bounds. The GBMST systems with systematic bits are more suitable over FSO links.Hence, in the following, we consider only the GBMST systems with systematic bits. We also find that, compared with the independent transmission with repetition code, GBMST systems improve diversity gain with only a slight reduction of transmission rate.

Example 2:We consider GBMST systems with repetition degree N = 2 and memory sequence m = (0, a) (a = 1, 2, 4, and 8). For a = 1, 2, 4, and 8, the corresponding transmission rates are 0.4950, 0.4902, 0.4808, and 0.4630, respectively. The error performances of GBMST systems when F = 1 and F = 2 are shown in figure 6, where we observe that

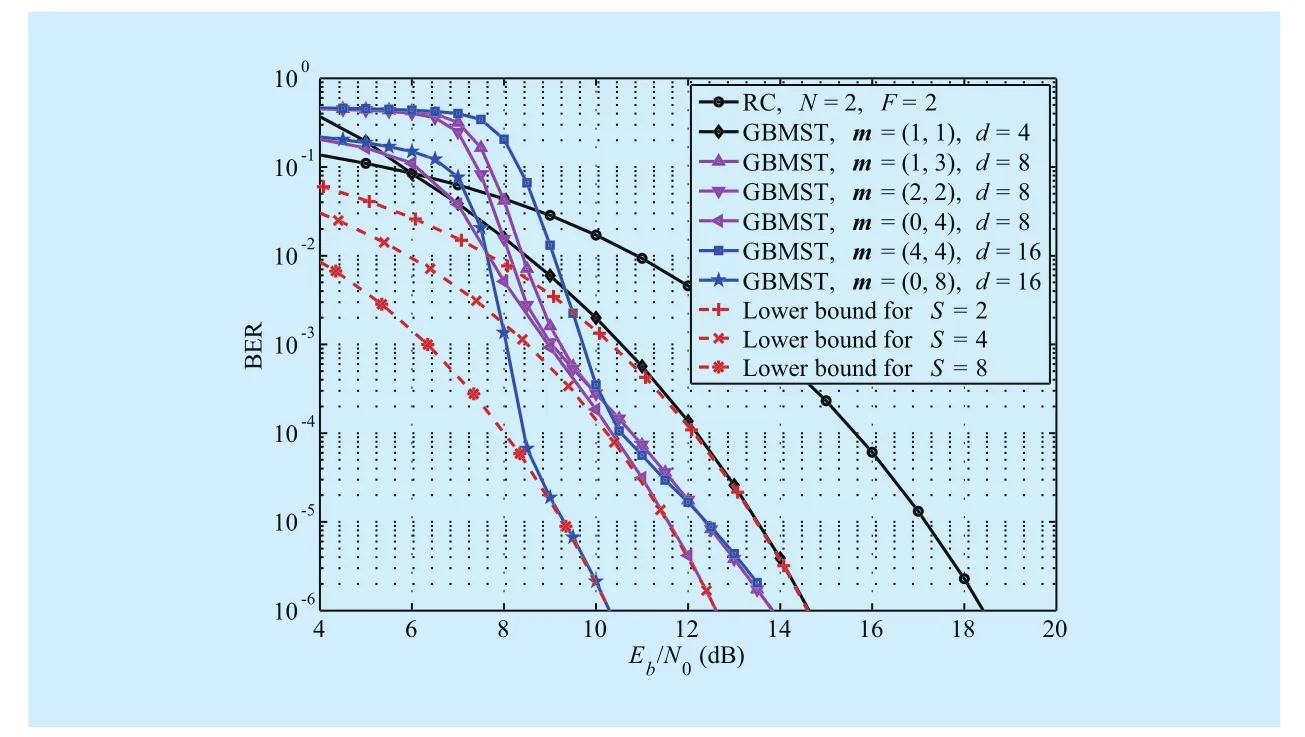
Fig. 5 Performance of the GBMST systems with repetition degree N = 2 under weak turbulence conditions when F = 2

1) For fixed decoding delay d = 2a, the BER performance of GBMST systems improves with the increase of memory a, and matches well with the corresponding lower bounds in the low BER region, indicating that the iterative sliding-window detection/ decoding algorithm is near optimal and full diversity is achieved in the low BER region under weak turbulence conditions. In a GBMST system,each information sequence experiences a + 1 channel fades when F = 1, and experiences a + 2 channel fades when F = 2. The system achieves diversity orders of a + 1 and a + 2,which correspond to F = 1 and F = 2, respectively. Compared with the independent transmission with repetition code, the GBMST

Fig. 6 Performance of the GBMST systems with repetition degree N = 2 and memory sequence m = (0, a) (a = 1, 2, 4, and 8) under weak turbulence conditions: (a)F = 1, (b) F = 2

Under weak turbulence conditions, the GBMST system with memory sequence m in the form ofcan effectively eliminate the effect of error propagation, and hence the BER performance curves of the GBMST systems match well with the corresponding lower bounds in the low BER region. Given the tightness of the lower bound, the system achieves diversity orders of a + 1 and a + 2, which correspond to F = 1 and F = 2, respectively.

5.2 Moderate Turbulence Conditions

For the moderate turbulence conditions, we setwhich results inandscheme obtains extra diversity order of a by Markov superposition, with only a slight reduction of transmission rate.

2) For fixed memory a = 4, the BER performance gets better as the delay d increases,but it does not improve much further beyond a certain decoding delay (roughly d = 6).However, the BER performance for a fixed memory sequence m cannot get lower than the genie-aided lower bound. In our simulations,we find that choosing a delay d, 2a < d < 3a,is sufficient to achieve the lower bound on the BER performance.

Example 3:We consider GBMST systems with repetition degree N = 2 and memory sequence m = (0, a) (a = 1, 2, 4, and 8). Figure 7 shows the BER performance of the systems when F = 2. From figure 7, we observe that the GBMST system with memory sequence m in the form of (0, a) can still work under moderate turbulence conditions. BER performance improves with the increase of transmission memory a, indicating potential diversity order of a + 2. However, when memory a is relatively large, the system with repetition degree N =2 is not available to approach the lower bound.When memory sequence m = (0, 8), there is a large gap (about 4 dB) between the simulation curve and the lower bound at BER = 10-5.

A GBMST system with memory sequence m in the form of (0, a) cannot effectively eliminate the effect of error propagation when a is relatively large under moderate turbulence conditions. When channel conditions become worse, it’s reasonable to adopt a lower rate repetition code as the basic code in GBMST system. To combat the error propagation under moderate or strong turbulence conditions, we employ GBMST systems with multiple transmission of systematic bits.

Example 4:We consider GBMST systems with repetition degree N = 3 and memory sequence m = (0, 0, a) (a = 1, 2, 4, and 8). For memories a = 1, 2, 4, and 8, the corresponding transmission rates are 0.3311, 0.3289, 0.3247,and 0.3165, respectively. Figure 8 shows the BER performance of the GBMST systems with repetition degree N = 3 when F = 3. We observe from figure 8 that, fixed d = 2a, BER performance of the GBMST systems improves with the increase of memory a, and matches well with the corresponding lower bounds in the low BER region, indicating that the iterative sliding-window detection/decoding algorithm is near optimal in the low BER region and full diversity is achieved. The GBMST systems obtain diversity order of a + 3. Compared with a repetition code with repetition degree N = 3, the GBMST scheme obtains extra diversity order of a by Markov superposition,with only a slight reduction of transmission rate.

5.3 Strong turbulence conditions

For the strong turbulence conditions, we setwhich results inand

Example 5:We consider GBMST systems with repetition degree N = 3 and memory sequence m = (0, 0, a) (a = 1, 2, 4, and 8).For memories a = 1, 2, and 4, termination length L = 50 is chosen for simulation and the corresponding transmission rates are 0.3311,0.3289, and 0.3247, respectively. When memory a = 8, a small L = 9 is chosen to limit the effect of error propagation on error performance, and the transmission rate is 0.2571 in this case. Figure 9 shows the BER performance of the GBMST systems when F = 3.We observe from figure 9 that, under strong turbulence conditions, simulation curves also match well with the corresponding lower bounds in the low BER region, indicating full diversity is achieved and diversity order of a + 3 is obtained. Compared with a repetition code with repetition degree N = 3, the GBMST scheme obtains extra diversity order of a by Markov superposition.

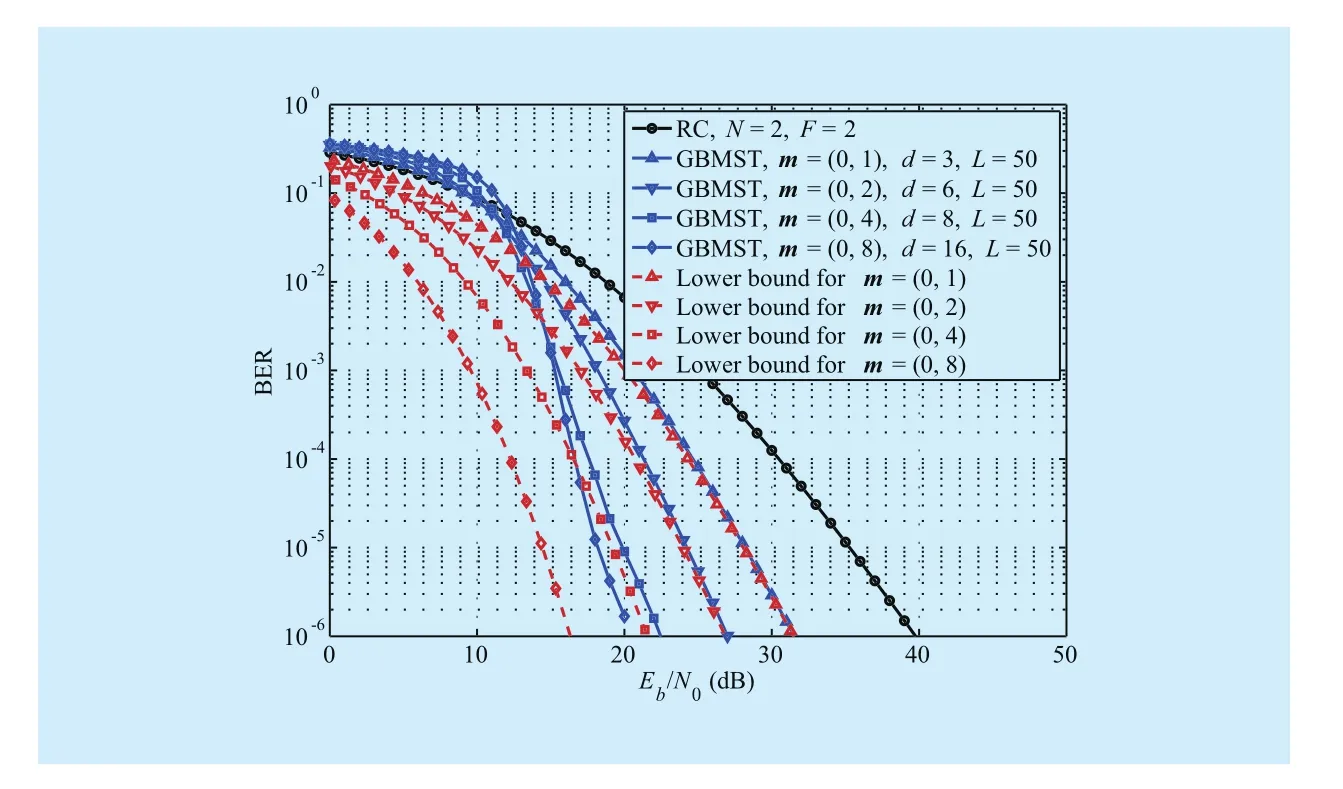
Fig. 7 Performance of the GBMST systems with repetition degree N = 2 and memory sequence m = (0, a) (a = 1, 2, 4 and 8) under moderate turbulence conditions when F = 2

5.4 Comparison with other coded schemes

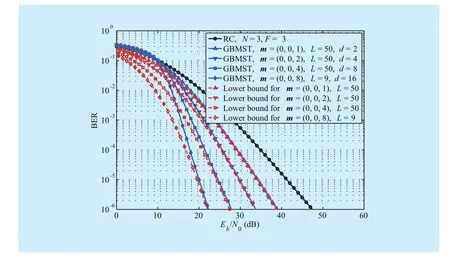
Fig. 9 Performance of the GBMST systems with repetition degree N = 3 under strong turbulence conditions when F = 3

Based on the equal decoding latencies, performance comparisons between GBMST systems, convolutional-coded systems, and LDPC-coded systems under moderate turbulence conditionsare performed.Consider GBMST systems with repetition degree N = 2, memory sequences m = (0, 1),(0, 2), (0, 4), and corresponding decoding delays d = 1, 2, 4, respectively, when F = 1.In convolutional-coded systems, the convolutional codes (CC) (1, 15/17) with constraint length 4 are chosen for comparison, whose BER performance over FSO links is investigated in [5]. In LDPC-coded systems, random(3,6)-regular LDPC codes of rate 0.5 [35] are chosen for comparison. The code length of each code is equal to the length of a decoding window in corresponding GBMST system,i.e.,Following [5], the coded sequences in convolutional-coded systems and LDPC-coded systems are randomly interleaved before transmitted over FSO links. In a GBMST system, there are d + 1 independent channel fades during a decoding window,while for comparison, each codeword experiences F = d + 1 independent channel fades in convolutional-coded systems and LDPC-coded systems. From figure 10, we observe that,when F = 2, the LDPC-coded system performs even worse than the convolutional-coded system, even though the LDPC code is more excellent over AWGN channels. We also observe that, GBMST scheme performs better than the other two schemes based on equal decoding latencies. Compared to the LDPC coded systems, GBMST systems with m = (0, 1), (0, 2),(0, 4) gain about 10 dB, 2.2 dB, 2.2 dB at the BER of 10-5, respectively.

VI. CONCLUSIONS

In this paper, we have presented a generalized block Markov superposition transmission(GBMST) to combat the channel fading induced by atmospheric turbulence. In GBMST scheme, each replica and its interleaved versions are transmitted in a block Markov superposition manner, with a possibly different memory. Based on analyzing an equivalent system, we have derived the genie-aided lower bound on BER performance of the GBMST scheme over FSO links. Simulation results show that, adopting the iterative sliding-window detection/decoding algorithm, the GBMST systems with appropriate settings can eliminate the effect of the interference among adjacent data blocks induced by Markov superposition. Under a wide range of turbulence conditions, the GBMST systems with appropriate settings can approach the derived lower bound, indicating that full diversity is achievable. Compared with traditional repetition-based diversity scheme, GBMST scheme can obtain extra diversity order with only a slight reduction of transmission rate. Based on the equal decoding latencies, comparisons between GBMST scheme, convolutional-coded scheme and the LDPC-coded scheme under moderate turbulence conditions have been performed, which show performance advantages of the GBMST scheme.

ACKNOWLEDGEMENTS

The authors would like to thank Dr. Kechao Huang for his insightful discussions and helpful comments. This work was partially supported by the Basic Research Project of Guangdong Provincial Natural Science Foundation (No. 2016A030308008), the National Natural Science Foundation of China (No.91438101 and No. 61501206), and the National Basic Research Program of China (973 Program) (No. 2012CB316100).

[1] M. Uysal, C. Capsoni, Z. Ghassemlooy, A. Boucouvalas, and E. Udvary, “Optical Wireless Communications: An Emerging Technology,” Springer, 2016.

[2] M. A. Khalighi and M. Uysal, “Survey on free space optical communication: A communication theory perspective,” IEEE Communications Surveys and Tutorials, vol. 16, no. 4, pp. 2231-2258, Jun. 2014.

[3] H. Kaushal and G. Kaddoum, “Optical communication in space: challenges and mitigation techniques,” IEEE Communications Surveys and Tutorials, vol. 19, no. 1, pp. 57-96, Aug. 2017.

[4] L. C. Andrews and R. L. Phillips, “Laser beam propagation through random media,” Bellingham, WA: SPIE press, 2005.

[5] F. Xu, A. Khalighi, P. Caussé, and S. Bourennane,“Channel coding and time-diversity for optical wireless links,” Optics Express, vol. 17, no. 2, pp.872-887, Jun. 2009.

[6] Y. Han, A. Dang, Y. Ren, J. Tang and H. Guo,“Theoretical and experimental studies of turbo product code with time diversity in free space optical communication,” Optics Express, vol. 18,no. 26, pp. 26978-26988, Dec. 2010.

[7] M. A. Khalighi, N. Schwartz, N. Aitamer, and S.Bourennane, “Fading reduction by aperture averaging and spatial diversity in optical wireless systems,” Journal of Optical Communications and Networking, vol. 1, no. 6, pp. 580-593, Nov. 2009.

[8] K. Wang, B. Liu, L. Zhang, Q. Zhang, Q. Tian, and X. Xin, “Review of coded modulation free space optical communication system,” China Communications, vol. 12, no. 11, pp. 1-17, Dec. 2015.

[9] S. M. Navidpour, M. Uysal, and M. Kavehrad,“BER performance of free-space optical transmission with spatial diversity,” IEEE Transactions on Wireless Communications, vol. 6, no. 8, pp.2813-2819, Aug. 2007.

[10] T. A. Tsiftsis, H. G. Sandalidis, G. K. Karagiannidis,and M. Uysal, “Optical wireless links with spatial diversity over strong atmospheric turbulence channels,” IEEE Transactions on Wireless Communications, vol. 8, no. 2, pp. 951-957, Feb.2009.

[11] H. E. Nistazakis, and G. S. Tombras, “On the use of wavelength and time diversity in optical wireless communication systems over gamma–gamma turbulence channels,” Optics & Laser Technology, vol. 44, no. 7, pp. 2088-2094, Oct.2012.

[12] K. Prabu, S. Cheepalli, and D. S. Kumar, “Analysis of PolSK based FSO system using wavelength and time diversity over strong atmospheric turbulence with pointing errors,” Optics Communications, vol. 324, pp. 318-323, Aug. 2014.

[13] S. Trisno, I. I. Smolyaninov, S. D. Milner, and C. C.Davis, “Characterization of time delayed diversity to mitigate fading in atmospheric turbulence channels,” in Proceedings of SPIE, pp. 589215.1-589215.10, Sept. 2005.

[14] C. H. Kwok, R. V. Penty, and I. H. White, “Link reliability improvement for optical wireless communication systems with temporal-domain diversity reception,” IEEE Photonics Technology Letters, vol. 20, no. 9, pp. 700-702, Mar. 2008.

[15] A. García-Zambrana, C. Castillo-Vázquez, and B.Castillo-Vázquez, “Rate-adaptive FSO links over atmospheric turbulence channels by jointly using repetition coding and silence periods,”Optics Express, vol. 18, no. 24, pp. 25422-25440,Nov. 2010.

[16] W. O. Popoola, Z. Ghassemlooy, H. Haas, E. Leitgeb, and V. Ahmadi, “Error performance of terrestrial free space optical links with subcarrier time diversity,” IET Communications., vol. 6, no.5, pp. 499-506, Mar. 2012.

[17] A. García-Zambrana, R. Boluda-Ruiz, C. Castillo-Vázquez, and B, Castillo-Vázquez, “Transmit alternate laser selection with time diversity for FSO communications,” Optics Express, vol. 22,no. 20, pp. 23861-23874, Oct. 2014.

[18] M. Karimi and M. Uysal, “Novel adaptive transmission algorithms for free-space optical links,”IEEE Transactions on Communications, vol. 60,no. 12, pp. 3808-3815, Dec. 2012.

[19] I. B. Djordjevic, “Adaptive modulation and coding for free-space optical channels,” Journal of Optical Communications and Networking, vol. 2,no.5, pp. 221-229, May 2010.

[20] H. AlQuwaiee, I. S. Ansari and M. S. Alouini, “On the performance of free-space optical communication systems over double generalized gam-ma channel,” IEEE Journal on Selected Areas in Communications, vol. 33, no. 9, pp. 1829-1840,Sept. 2015.

[21] S. M. Aghajanzadeh and M. Uysal, “Performance analysis of parallel relaying in free-space optical systems,” IEEE Transactions on Communications,vol. 63, no. 11, pp. 4314-4326, Nov. 2015.

[22] Y. Tang, M. Brandt-Pearce and S. G. Wilson, “Link adaptation for throughput optimization of parallel channels with application to hybrid FSO/RF systems,” IEEE Transactions on Communications,vol. 60, no. 9, pp. 2723-2732, Sept. 2012.

[23] V. Jamali, D. S. Michalopoulos, M. Uysal and R.Schober, “Link allocation for multiuser systems with hybrid RF/FSO backhaul: delay-limited and delay-tolerant designs,” IEEE Transactions on Wireless Communications, vol. 15, no. 5, pp.3281-3295, May 2016.

[24] X. Ma, C. Liang, K. Huang, and Q. Zhuang, “Block Markov superposition transmission: Construction of big convolutional codes from short codes,” IEEE Transactions on Information Theory,vol. 61, no. 6, pp. 3150-3163, Jun. 2015.

[25] K. Huang, X. Ma, and B. Bai, “Systematic block markov superposition transmission of repetition codes,” in Proceedings of IEEE International Symposium on Information Theory, Barcelona,Spain, pp. 1929-1933, Jul. 2016.

[26] X. Zhu, and J. M. Kahn, “Free-space optical communication through atmospheric turbulence channels,” IEEE Transactions on Communications, vol. 50, no. 8, pp. 1293-1300, Aug. 2002.

[27] M. A. Al-Habash, L. C. Andrews, and R. L. Phillips,“Mathematical model for the irradiance probability density function of a laser beam propagating through turbulent media,” Optical Engineering,vol. 40, no. 8, pp. 1554-1562, Aug. 2001.

[28] H. Tang, W. Xu, and G. Wu, “Average capacity of OAM-multiplexed FSO system with vortex beam propagating through non-Kolmogorov turbulence,” China Communications, vol. 13,no.10, pp. 153-159, Oct. 2016.

[29] V. W. S. Chan, “Free-space optical communications,” Journal of Lightwave Technology, vol. 24,no. 12, pp. 4750-4762, Dec. 2006.

[30] J. Anguita, I. Djordjevic, M. Neifeld, and B. Vasic,“Shannon capacities and error-correction codes for optical atmospheric turbulent channels,”Journal of Optical Networking, vol. 4, no. 9, pp.586-601, Sept. 2005.

[31] M. Uysal, J. Li, and M. Yu, “Error rate performance analysis of coded free-space optical links over gamma-gamma atmospheric turbulence channels,” IEEE Transactions on Wireless Communications, vol. 5, no. 6, pp. 1229-1233,Jun. 2006.

[32] W. Gappmair, and M. Flohberger, “Error performance of coded FSO links in turbulent atmosphere modeled by gamma-gamma distributions,” IEEE Transactions on Wireless Communications, vol. 8, no. 5, pp. 2209-2213, May 2009.

[33] G. D. Forney, “Codes on graphs: normal realizations,” IEEE Transactions on Information Theory,vol. 47, no. 2, pp. 520-548, Feb. 2001.

[34] X. Zhu, and J. M. Kahn, “Performance bounds for coded free-space optical communications through atmospheric turbulence channels,” IEEE Transactions on Communications, vol. 51, no. 8,pp. 1233-1239, Aug. 2003.

[35] R. Gallager, “Low-density parity-check codes,”MIT Press, Cambridge, MA, 1963.