地下风机房结构受力分析与研究

钱文斐

（上海市政工程设计研究总院（集团）有限公司，上海市 200092）

相关专业

地下风机房结构受力分析与研究

钱文斐

（上海市政工程设计研究总院（集团）有限公司，上海市 200092）

纵向式通风井送排式通风是当前和未来特长隧道的主流通风模式。通过对地下风机房隧道群结构体系的核心组成部分——地下风机房受力及变形的分析，得出了如下结论：在Ⅲ级围岩的条件下，端头墙交界处受力不利，应加强结构设计；端头墙对拱部、边墙部5m范围内有一定的约束支撑作用；地下风机房的总体位移值较小。以上结论为地下风机房的结构设计提供了一定程度的参考价值。

特长隧道；纵向式通风井送排式通风；地下风机房；端头墙

0 引言

20世纪80年代以后修建的特长隧道大多采取纵向式通风井送排式通风，由此可见纵向式通风井送排式通风是当前和未来特长隧道的主流通风模式，而这种通风模式的核心是建立在地下风机房隧道群的结构体系之上。地下风机房作为地下风机房隧道群结构体系的“核心”，目前国内学者及设计师关于其结构受力状态方面的研究成果较少，因此有必要进行深入研究。

1 研究对象

以某隧道地下风机房隧道群为例，对地下风机房的内力、变形等情况进行分析研究。

1.1 计算条件

具体的计算条件如下：

（1）地下风机房隧道群洞身所处围岩级别为Ⅲ级围岩。

（2）组成地下风机房隧道群各洞室的尺寸见表1，相对位置关系如图1和图2所示。

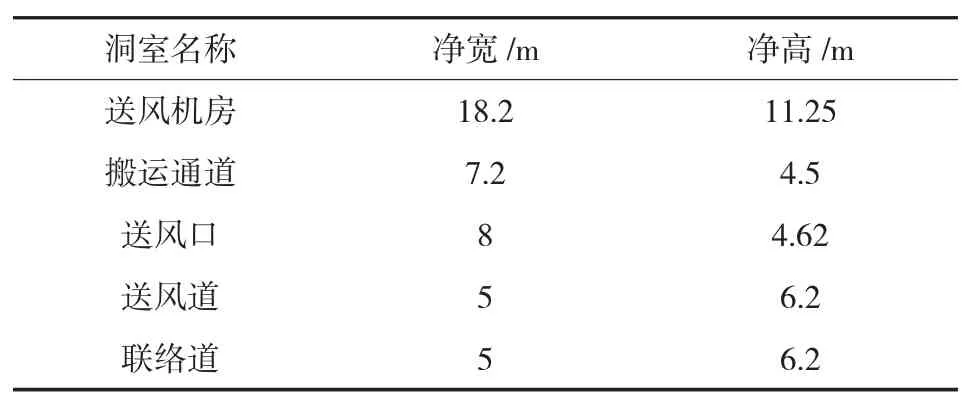
表1 各洞室尺寸一览表

图1 地下风机房隧道群平面布置图（单位:mm）

（3）对于组成地下风机房隧道群的各个洞室均只考虑初期支护作用，对于送风机房，采用C25喷射混凝土20 cm，其余洞室则均采用10 cm。

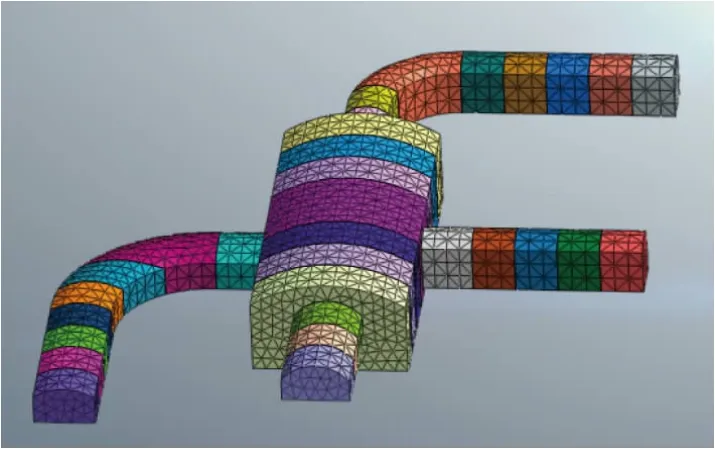
图2 地下风机房隧道群各洞室空间位置关系

（4）施工工序：搬运通道→送风机房→送风口、送风道、联络道。

1.2 荷载确定

采用“地层-结构”法。

2 计算结果

2.1 拱顶最大主应力值

拱顶最大主应力值分布如图3所示。

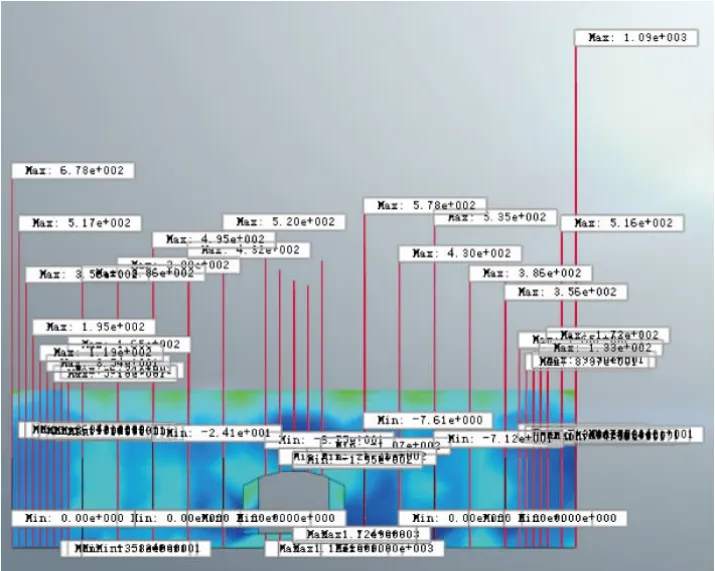
图3 拱顶最大主应力值分布图

由图3可以得出：

（1）拱顶最大主应力值在端头墙位置出现最大值，分别为678 kPa、1 090 kPa，这是由于端头墙位置结构形式发生突变，从而出现了应力集中现象。但是距离端头墙3 m、3.5 m时，最大主应力值迅速降低至最小值，分别为51.8 kPa、89.7 kPa。这说明应力集中影响范围在距离端头墙3～3.5 m,经分析认为：距离端头墙3～3.5 m时，拱顶部分由于端头墙支承作用，因此受力条件较之有利，最大主应力值最小。

（2）在开洞位置处的最大主应力值较之未开洞处小，经分析认为，这是由于开洞位置削弱了边墙对拱顶的支撑作用，使得拱顶的应力部分得到了一定程度的释放。

（3）在开洞及端墙影响范围之外的区域，其最大主应力值居中，在390～550 kPa范围内，这是因为相对而言，此区段既没有受到端墙支承作用也没有应力释放的渠道。

2.2 边墙部位最大主应力值

左侧边墙最大主应力值分布如图4所示。

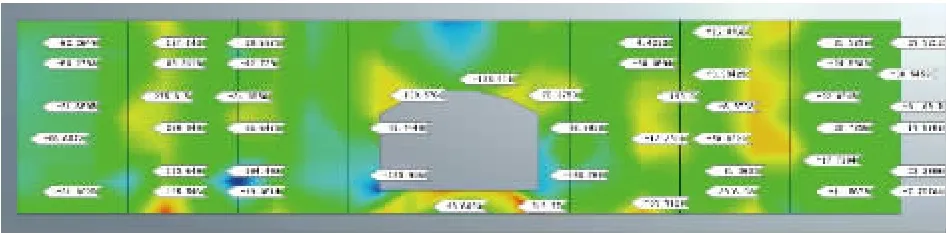
图4 左侧边墙最大主应力值分布图

由图4可以得出：

（1）两侧边墙距离端头墙5 m范围内，最大主应力值基本为负值，即压应力值，且数值均较小，基本在80 kPa以下。经分析认为，这是因为此段边墙由于端头墙的支撑作用，因此受力条件较之有利。

（2）在开洞位置的拱顶至拱腰以及边墙部位，最大主应力为压应力，而拱腰至拱脚及底板，最大主应力为拉应力。

（3）在开洞及端墙影响区范围外，最大主应力大部分为压应力，小部分为拉应力（不大于300 kPa）。

右侧边墙最大主应力值分布如图5所示。

图5 右侧边墙最大主应力值分布图

由图5可以得出：

（1）两侧边墙距离端头墙5 m范围内，最大主应力值大多为压应力值，虽小部分为拉应力值（30 kPa以下），但数值较小。经分析认为，这是因为此段边墙由于端头墙的支撑作用，因此受力条件较之有利。

（2）在开洞位置的拱部、边墙及底板的最大主应力值均为拉应力，其中拱部接近1 000 kPa，边墙在500～800 kPa范围，底板超过2 000 kPa；拱脚、边墙底均为压应力值。

（3）在开洞及端墙影响区范围外，最大主应力大部分以拉应力为主，小部分为压应力。

通过对左、右边墙的对比得出：

（1）由于受到端头墙支撑作用的有利条件，在距离端头墙5 m范围内的边墙受力条件均较为有利。

（2）开洞位置处的最大主应力值分布情况及数值均存在着较大差异。

（3）总体而言，右侧边墙的支护处于相对不利的状态。

2.3 端头墙最大主应力值

端头墙最大主应力值分布如图6和图7所示。

图6 与送风口交界处端头墙

图7 与送风道交界处端头墙

由图6和图7可得出：

（1）两侧端头墙的最大主应力值分布趋势基本相同。在拱部及底部均出现了一定范围的拉应力值，拱顶位置处最大值分别为1 912 kPa、1 931 kPa；底部位置处最大值分别为2 050 kPa、1 739 kPa；在洞室边墙部位均出现了压应力值，但与送风道交界处的应力值较小，为50 kPa左右，与送风口交界处的应力值较大，为450 kPa左右。

2.4 拱顶竖向位移

根据送风机房拱顶竖向位移分布情况，由图8和图9可以看出，在地下风机房中间部位的竖向位移相对较大，因此拟针对此部位竖向位移在施工过程中的变化情况进行分析。

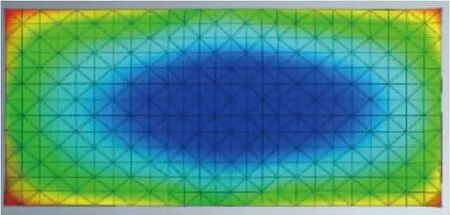
图8 拱顶竖向位移平面分布云纹图（第26施工步）

图9 拱顶竖向位移纵剖面分布云纹图（第26施工步）

拱顶竖向位移随施工步变化情况如图10所示。

从图10可以看出：

（1）中部位置处由于临空面较大，因此竖向位移值也较大。

（2）施工步11～18,竖向位移相对变化较快，施工步18～26，竖向位移变化不大,这说明当送风机房开挖支护施作后，后续洞室的施作对送风机房拱顶的沉降影响不大。

（3）施工步11～18,右侧比左侧竖向位移值大，但随着后续洞室施作，两者的竖向位移值较为接近。

2.5 边墙部位横向位移

根据地下风机房边墙部位的横向位移分布情况（见图11），可以看出，在地下风机房中间部位的横向位移分布情况相对较为复杂，但总体数值在10-2mm级别，故可以得出，横向位移影响不大，但需指出的是，与搬运通道、联络道交界位置的下部区域出现了与其余区域不同的位移方向，此处位移方向向外侧，而其余区域则向内侧。

图11 边墙水平位移分布云纹图（第26施工步）

3 研究结论

根据以上分析结果，可以得出以下结论：

（1）与端头墙交接处，由于结构形式发生突变，结构受力由于应力集中处于较为不利的情况，因此设计中需加强此处的结构设计。

（2）端头墙对于风机房的拱部、边墙部均有一定范围的约束支撑作用，这种作用有利于结构的受力，约束范围约距离端头墙5 m。

（3）与我们通常所认为的“开洞宽度越大，结构受力越不利”不同，右侧边墙虽然开洞宽度较左侧小，但右侧边墙相对而言受力状态处于不利的情况。因此理论上右侧边墙支护强度应高于左侧。

（4）对于端头墙而言，开洞位置的拱部、底部处于相对不利的受力状态，而边墙部则相对有利，施工中应重点观察开洞位置的拱部、底部的支护，以防止支护在以上部位发生破坏。

4 结语

虽然本文得出了关于地下风机房受力性状的一些结论，可以为相关设计提供参考依据，但考虑到计算假定与围岩实际的本构关系存在一定程度的差异，因此尚需在施工中通过监控量测以进行验证及修正，从而更好地为工程设计服务。

[1]翟正平.宝塔山隧道地下风机房布置与施工[J].山西交通科技, 2010(6):54-55.

[2]翟正平.宝塔山隧道地下风机房设计与调整[J].现代隧道技术, 2012，49(10):99-103.

[3]熊文亮.华蓥山特长公路隧道地下风机房设计与施工[J].隧道建设,2012，32(10):670-674.

[4]张开顺,余斌,申家喜.夹活岩特长公路隧道竖井设计及施工方法探讨[J].公路,2006(5):213-215.

[5]吴德兴，李伟平，高翔，郭霄，郑国平，郭洪雨.浙江省高速公路特长隧道运营通风土建结构的设计实践 [J].公路,2011(8): 287-292.

[6]王明年,田尚志,郭春,李玉文.公路隧道通风节能技术及地下风机房设计[M].北京:人民交通出版社,2012.

[7]JTG F60—2009，公路隧道施工技术规范[S].

[8]JTG/T D70—2010，公路隧道设计细则[S].

[9]JTG/T D70/2-02—2014，公路隧道通风设计细则[S].

U453.5

A

1009-7716（2017）03-234-03

10.16799/j.cnki.csdqyfh.2017.03.065

2016-12-26

钱文斐（1977-），男，江苏镇江人，高级工程师，主要从事岩土工程与地下结构设计研究工作。