基于非视距鉴别的无线传感器网络混合定位算法的研究与设计
胡婷++张铮
摘要:针对非视距误差会导致无线传感器网络定位系统定位精度严重下降及单一定位算法易受环境影响等问题,本文提出了基于NLOS鉴别的无线传感器网络混合定位算法。通過NLOS鉴别算法从各个锚节点记录时间信息中剔除具有NLOS误差的锚节点,并利用混合定位算法完成最终对标签节点的定位。仿真结果表明该算法有效地剔除了NLOS对系统定位结果的影响,并且,通过混合定位算法大大提升了系统定位性能。
关键词:非视距;到达时间差;到达角度
中图分类号:TP393 文献标识码:A 文章编号:1007-9416(2017)02-0150-03
当下,越来越多的行业都产生了大量无线定位的需求,这就引领出了国内外关于无线定位技术研究的浪潮[1-6]。当前广泛使用的无线节点测距方法大体有:基于信号到达强度的测距方法(RSSI)[7]、基于信号到达角度的测距方法(AOA)[7]、基于信号到达时间的测距方法(TOA)[8]以及基于信号到达时间差的测距算法(TDOA)[9]等。
无线传感器网络系统的定位误差来源主要有以下几个方面:(1)由于信道环境恶劣而产生的测量误差;(2)定位算法导致定位方称非线性而产生的计算误差[10]。而由于非视距(NLOS)所造成的误差是测量误差重要的组成部分。传统的节点定位方法如:Chan算法[11]、Taylor级数展开法[12]等都未将NLOS误差考虑在定位算法中,因此在节点在NLOS环境中通信时,两种方法的定位性能都大大下降。
基于传统方法依赖先验信息这一情况,本文提出了一种改进的方法利用TOA与TDOA在非视距情况下的一些特性,消除非视距误差的影响。
同时,在现今的无线传感器网络定位系统中,常常利用单个的定位方法来完成最终的标签定位工作,而这些方法都有各自的缺陷。因此本文提出了一种基于TDOA与AOA混合定位的方法,旨在综合该两种定位算法各自的优点,达到提升系统定位精度的目的。
本文算法结构为:(1)利用本文提出的NLOS鉴别算法从锚节点中筛选出有非视距通信情况的锚节点,并将该节点记录的TOA信息删除;(2)通过剩余的TOA信息结合锚节点可以记录的AOA信息,并利用已有的定位方程完成标签节点位置信息的计算。
1 非视距鉴别算法
为了辨别定位系统中是否存在非视距锚节点,需要利用特定算法进行鉴别。
定位系统中,锚节点j与标签之间在时刻测量的TOA信息可以表示为:
(1)
其中表示系统测量的TOA信息,代表真实应得的TOA信息,代表系统的测量噪声,在这里认为噪声服从均值为0,方差为的高斯分布,表示锚节点j与标签之间由于非视距误差而导致的时延,其均值为,方差为。因此如何求出或判断出TOA信息中是否存在该时延量成为解决NLOS问题的关键。
针对存在时延的问题,本文提出了一种算法:算法中假设系统中锚节点的位置都已提前测量,且锚节点之间无障碍物能够互相通视。在NLOS鉴别算法运行过程中,利用锚节点之间能够获得的通信TOA信息,计算锚节点之间通信的到达时间差也就是TDOA信息,记录多组该信息,并统计其均方差记录,作为参考均方差记为。用相同的方法记录并计算锚节点与标签之间的TDOA信息并统计多组均方差记为,其中表示锚节点1与锚节点2之间TDOA信息的均方差,表示锚节点个数。将参考均方差与锚节点与标签之间计算的均方差进行比对,若差距较大则计算出该组TDOA信息的两个锚节点与标签之间可能存在NLOS,经过多组判断从中找出具有NLOS通信的锚节点,最终完成对NLOS锚节点的剔除。
2 混合定位算法
基于TDOA与AOA混合定位的技术是结合TDOA与AOA信息完成定位的一种方法。在定位过程中,标签节点广播信号,锚节点记录TOA和AOA信息,由于各个锚节点和标签节点之间的距离不等,可以通过TOA信息计算各个锚节点的相对于标签节点的TDOA信息,利用TDOA信息可以计算出各个锚节点相对于标签节点的距离差,结合已经获得的信号AOA信息,利用混合定位算法可以完成对标签的定位计算。
这里我们只考虑二维情况下的定位。假设锚节点坐标信息用来表示,标签坐标为,则锚节点和标签之间的距离信息可表示为,由此可得:
(2)
令,将其带入公式(2)化简可得:
(3)
令,依据此继续化简公式(3)可得:
(4)
锚节点上加装的小型天线阵列可获得的标签广播信号到达锚节点的角度信息表示为:
(5)
联立公式(4),公式(5)并变换矩阵形式可得:
(6)
令矩阵中:
则可得:
(7)
从上式可以看出,B矩阵的行列式值为且从锚节点1获得的AOA信息可知矩阵行列式值不为0,因此存在逆矩阵,则可变换得:
(8)
令:
(9)
则有:
(10)
将上述公式带入可得:
(11)
其中:
(12)
(13)
(14)
从这些等式中可以看出,式中只有一个未知数,即为标签和锚节点之间的距离信息。因此,可以通过距离信息完成定位。
3 仿真性能分析
3.1 不同非视距时延下的仿真分析
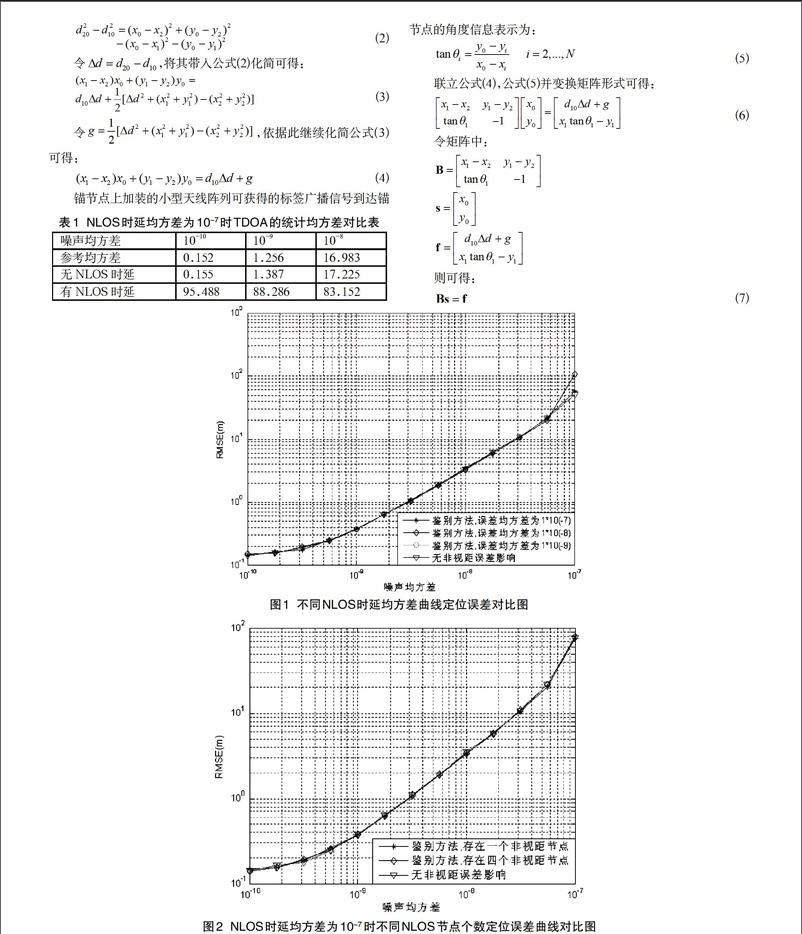
如图1所示为系统只有一个非视距锚节点,所得到的不同NLOS时延情况下的定位精度分析结果图。纵轴表示定位误差,横轴表示TOA测量噪声的均方差。
由仿真结果可以看出算法有效地降低了NLOS误差对定位的影响。
从上表1中可清楚看出,NLOS时延对TDOA的影响是非常大的,因此本文方法可以有效地鑒别并剔除NLOS时延的影响。
3.2 不同非视距节点个数下的仿真分析
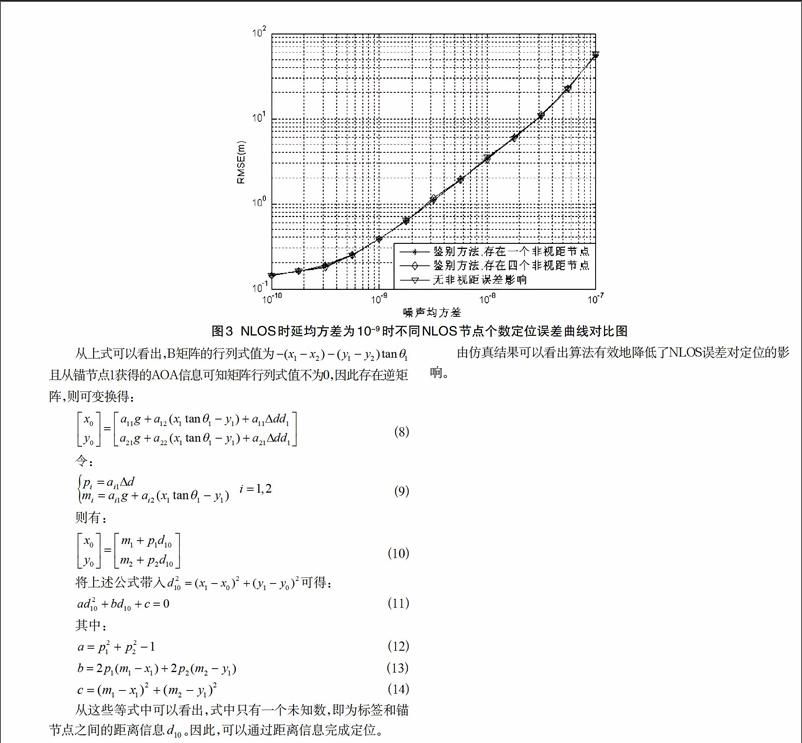
如图2,图3所示为在不同NLOS锚节点个数及NLOS时延均方差情况下标签定位误差仿真分析对比图。
由仿真结果可以看出算法有效地降低了NLOS误差对定位的影响。
4 结语
本文提出了一种非视距误差的鉴别算法,利用锚节点之间通视的先验条件,通过非视距情况下标签与锚节点之间的测量TOA信息会起伏变化这一特性剔出非视距锚节点。同时,本文还提出了一种混合定位算法,成功解决了定位方法单一容易受环境影响的问题,降低了系统定位需求的锚节点个数,在不影响定位精度的情况下降低了系统成本。通过仿真分析验证,证明了该两种方法的有效性。
参考文献
[1]孙利民,等编著.无线传感器网络[M].清华大学出版社,2005.
[2]李哲涛,李仁发,魏叶华.无线传感器网络中时间同步与测距协同算法[J].计算机研究与发展,2010(04)
[3]杜存功,丁恩杰,苗曙光,王满意,朱微维.无线传感器网络改进型节点定位算法的研究[J].传感器与微系统,2010(01).
[4]王亮,曹建安.无线传感器网络定位算法研究进展[J].现代电子技术,2011(23).
[5]刘志华,赵寿君,齐冬梅.三维无线传感器网络节点的序列垂心定位[J].无线电工程,2010(04).
[6]杜存功,丁恩杰,苗曙光,王满意,朱微维.无线传感器网络改进型节点定位算法的研究[J].传感器与微系统,2010(01).
[7]张怡,席彦彪,李刚伟,赵凯华.基于卡尔曼滤波的TDOA/AOA混合定位算法[J].计算机工程与应用,2015(20).
[8]汪苑,林锦国.几种常用室内定位技术的探讨[J].中国仪器仪表,2011(02).
[9]王鹏,雷斌,张洪顺,魏勇.TDOA定位系统的设计与实现[J].中国无线电,2013(01).
[10]李军,张会清.一种室内定位中NLOS误差抑制算法[J].控制工程,2009,16(7):117-119.
[11]李娅菲,朱烜璋.非视距条件下的测距信息融合定位方法研究[J].电子测量与仪器学报,2015(05).

