柔性挡土结构空间土压力性状的三维有限元分析
王成华+王泽


摘要:为了研究基坑开挖对柔性挡土结构土压力空间分布规律的影响,进而为基坑的设计与安全防护提供相应依据,用ABAQUS建立基坑开挖的有限元模型,分析基坑开挖对挡土结构“单片墙”空间土压力的影响。考虑了不同刚度、有无支撑、不同开挖深度对挡土墙不同部位的土压力分布和挡土墙位移的影响,并将挡土结构三维土压力分布规律与二维数据进行了对比,验证了三维有限元模拟的必要性,对比了加支撑与否对基坑土压力空间分布的影响。结果表明:“单片墙”主动区土压力呈马鞍状分布,挡土结构后部土体的影响范围和下部土体的影响范围都约为2倍开挖深度;支撑结构极大地限制了墙后土体危险区域的范围,但是对墙下土体的限制作用并不是很明显。
关键词:空间土压力;挡土结构;基坑开挖;有限元分析;开挖深度
中图分类号:TU432 文献标志码:A
文章编号:1673-2049(2017)02-0033-08
Abstract:In order to investigate the influence of foundation pit excavation on the earth pressure spatial distribution law of flexible retaining structure, and to provide references for the design and safety protection of foundation pit,the finite element model of foundation pit excavation was established by ABAQUS and the influence of the foundation pit excavation on spatial earth pressure of retaining structure “monolithic wall”. The influences of different stiffness, with and without supports, different excavation depths on the earth pressure distribution and the displacement of different parts in retaining wall were considered. The three-dimensional earth pressure distribution of the retaining structure was compared with the two-dimensional data, and the necessity of three-dimensional finite element simulation was verified. The results show that “monolithic wall” active earth pressure zone appears a saddle shaped distribution, and the influence ranges of the behind and the bottom of retaining structure are about 2 times of excavation depth.Supporting structure greatly limits the scope of earth dangerous area behind the wall, but has no obvious limiting effect on the bottom of retaining structure.
Key words:space earth pressure; retaining structure; excavation of foundation pit; finite element analysis; excavation depth
0引 言
对于传统的基坑工程,平面分析方法计算简便,适用性好,工程中经常采用考虑了土体和支护结构的二维有限元分析方法,但是深基坑是一个三维空间结构,具有长、宽、深同等量级的几何尺寸,三维空间效应非常显著,基于经典平面土压力理论未能在实际设计中体现深基坑很强的空间效应,也不适应深基坑设计的需要,这是导致不少工程设计存在安全性隐患及经济性不高的重要因素。作用在挡土结构上的主要荷载是侧向土压力,其大小和分布与土压力的位置有关,由于空间效应的存在,不同位置的土压力分布规律也不一致。
近年来,国内外对于挡土结构土压力与位置的关系进行了一定的研究,杨雪强等[1]以无黏性土为例,基于土的塑性上限理论及极限平衡分析理论对基坑支护结构土压力进行了探讨,但是难以解决复杂破坏机理的稳定问题和反映相应的本构关系。俞建霖等[2]采用Duncan-Chang本构模型、Goodman接触单元建立三维有限元模型,对基坑的空间性状进行了分析,并与二维结果进行对比,初步得出土压力空间分布規律:基坑边角处围护结构的水平位移和被动土压力较小,随后逐步增大,至基坑中部达到最大值,而主动土压力的变化规律则相反。Simpson[3]通过基坑试验在挡土墙入土深度较浅的前提下得到抗角效应不存在的结论,本文对较深的入土深度进行了分析。Lee等[4]通过对实际工程的数值模拟和实测数据分析,指出角部效应能减小支护结构变形,三维分析比二维分析能更好地预测变形的发展。陈页开等[5]考虑压顶梁的约束作用和空间效应,从工程实例的角度分析了围护结构的内力和变形规律,具体分析了桩顶水平位移、桩身负弯矩,结果表明,桩顶水平位移在基坑中部截面最大,两边最小,最大负弯矩与桩顶水平位移有相反规律,并考虑了基坑尺寸对角效应的影响,但是缺乏对于空间效应具体的对比分析并得出相应规律。崔春义等[6]基于ABAQUS建立基坑体系二维有限元模型并对土压力进行了研究,分析了4个开挖阶段墙体位移的情况,但是适用范围有限,对于空间效应大的深基坑适用性差。卢坤林等[7]给出了平面土压力计算公式,较好地反映了主动土压力与位移的关系,能够计算不同位移时主动土压力的大小,对空间土压力计算提供了思路;黄亚娟等[8]给出了刚性结构物竖直土压力的双剪统一解;贾萍等[9]基于前人平面理论和双剪统一强度理论推导出了空间主动土压力双剪统一解的简化计算公式;Bono等[10]认为基坑侧向变形中部最大,二维变形比三维变形和实测变形都大,坑角抑制了邻近变形的发展。其他学者也进行了相应的三维有限元研究[11-15],但是由于土体的复杂性和影响因素的多样性,已经提出的考虑基坑空间效应的基坑变形分析方法和分析结果还很难反映深基坑工程空间效应的真实特性。
本文基于整体结构进行建模,采用ABAQUS数值分析软件建立三维有限元模型,主要研究支护结构基坑开挖对土体变形和土压力分布的影响,以及坑角的限制作用对基坑土体土压力分布的影响。本文在考虑土体和支护结构空间协同作用的基础上,选取了长度方向的单面墙体进行分析,研究了单面墙的土压力在不同部位的空间分布规律、围护结构的变形、土体开挖变形影响范围,同时与二维平面应力问题进行了比较。
1有限元模型及计算参数
1.1计算假定
本文采用有限元软件ABAQUS进行模拟,在没有做出说明的情况下,改变其中一个参数时其余参数保持不变。计算基本假定为:
(1)计算域内土体为各向同性、均质和连续土體,土体采用弹塑性模型,采用Mohr-Coulomb破坏准则。
(2)挡土墙、支撑采用线弹性模型,挡土墙、支撑都采用实体单元。
(3)挡土墙与土体紧密相连,不产生滑移。
(4)不考虑地下水影响。
1.2计算模型
根据结构对称性及简化计算,模型取整体1/2进行分析。对于土和挡土墙,采用八节点线性六面体减缩积分C3D8R单元,计算边界原则上要满足基坑开挖结构受力后不再产生变形影响。根据前人的研究成果[16]分析支护结构的变形,侧向边界取坑壁外3倍基坑开挖深度,模型底部边界距离支护结构2倍开挖深度,考虑粉质黏土黏聚力过大而存在的自立高度问题,基坑顶部施加36.5 kPa的均布荷载,并在基坑顶部设置1道支撑。作如下说明:
(1)计算区域尺寸为100 m×45 m×40 m,即墙后水平尺寸是基坑深度的3倍,坑底模型竖向深度取基坑开挖深度的2倍。
(2)基坑深度为9 m,挡土墙高度为20 m,厚度为0.6 m,完整基坑横向尺寸为40 m×30 m。
(3)基坑在地表标高设1道支撑,支撑截面尺寸为0.4 m×0.4 m。
(4)基坑开挖过程分3步,每层开挖3 m深度。
(5)位移同坐标系正向为正,反之为负,模型平面结构、网格图及剖面图如图1~3所示。
1.3计算参数
为考虑墙体工作状态下微裂缝产生与发展的影响,本文数值模拟分析时参考了文献[17]的实例,取弹性模量E为压缩模量Es的8倍,即E=8Es。参考工程实例和ABAQUS经验值[18],在计算分析时弹性模量取为标准值乘以0.8的折减系数。本构模型参数见表1,挡土墙、支撑计算参数见表2。
1.4模拟步骤
(1)建立相应模型,按照相应的参数给模型设定参数,对每个施工步赋予相应的加载条件、边界条件和相互作用。
(2)对模型施加体力和荷载,平衡地应力。
(3)激活基坑边界顶部横撑。
(4)开挖第1层土体,开挖深度为3 m。
(5)开挖第2层土体,开挖深度为3 m。
(6)开挖第3层土体,开挖深度为3 m。
2计算结果分析
2.1挡土墙应力分布规律及影响
选取无支撑的有限元模型进行计算,施加了36.5 kPa的荷载,应力三维分布如图4所示。基坑三维尺寸在同一量级,并非前人所简化的传统土压力计算模式,计算结果是一个均匀分布的平面,初步分析本文结果是一个扭曲的曲面,同一高度两边的土压力大,中间的土压力小,曲面呈“马鞍形”,但并不是完全地按照压力递减的顺序变化,由于坑角效应的影响,靠近挡土墙边的土压力很大,因此土压力沿墙位置的变化呈现先减小后增加,然后平缓变化到挡土墙中部的一个趋势。应力在减小过程中存在一个拐点,在大约一半开挖深度时土压力变化趋于平缓。顶部初始应力由于荷载作用,土压力并不是从0开始,初始主动区的应力值小于荷载应力。
任取挡土墙边长上一点观察不同高度的土压力分布,规律是先平缓增加,然后有一个凹陷,再继续平缓增加,呈现“R”型非线性分布,与一些工程中实测得到的土压力“R”型分布相吻合,即靠近基坑边缘土压力大、中部土压力小的一个基本规律。
2.2支撑对于挡土墙应力、位移分布的影响
图5给出了x=0处土压力值沿基坑深度方向的分布规律。由图5可见,顶部支撑对于土压力的分布影响并不明显,由于荷载的存在,土压力值并不是从0开始,不加支撑的土压力值要比加支撑的土压力值稍大,这是由于坑角效应的限制作用占了主要作用。
对比不加支撑的主动区土压力分布,两者分布规律大致相同,同样为一扭曲的曲面。加支撑顶端的土压力分布受到了支撑的限制作用,顶端的土压力近似相同。图6,7给出了3个截面(x=0,x=0.1A,x=0.5A)处应力值的对比,加支撑对最顶端的应力变化影响较大,顶部应力分布均匀,近似相同,应力随着挡土墙的宽度变化较小,更加接近平面应力状态,不加支撑的土压力在顶部差别很大,这主要是受空间效应的影响,所以距离基坑边缘越近,土压力越大。随着基坑深度的变化,x=0.1A,x=0.5A处在大约6 m深度的加支撑曲线斜率有一定减小,x=0处并没有相应的变化,在靠近基坑边缘处的空间效应较强,主要受空间效应影响,应力近似呈直线。对比x=0.1A和x=0.5A处的曲线,在开挖面上部靠近基坑边缘的x=0.1A处土压力更大些,开挖面以下远离基坑边缘的x=0.5A处土压力更大些,说明在水平方向土压力并不是完全的递减状态,在同一高度处的土压力会有一定的回弹,开挖面以下的挤土作用对土压力的分布也起了一定的重分布作用。
图8,9分别给出了不加支撑和加支撑挡土墙的位移。由图8,9可知,三维变形位移场分布规律与二维常规的规律并不相同,虽然中部土压力值最小,但是对应的位移是最大的。由于基坑开挖的原因,挡土墙上部位移很大,随着深度的增加,变化的曲率也在逐渐增大,变形量迅速减小,挡土墙下部4 m的位移变化量很小,但是底部还是存在一定的位移。由于坑角效应的影响,基坑边缘一段范围内位移几乎不发生变化,坑角对挡土结构存在较强的约束作用,距基坑角部距离达到一定值后,变形的曲率迅速增大,变形值有了非常明显的变化,这也符合目前一些基坑坑角效应的研究。由于顶部支撑的限制,顶部及其附近的位移量很小,挡土墙中间的位移大,四周的位移小,加支撑的变形图与文献[2]中图4完整基坑变形图放大100倍效果相同,预测的规律也是相符合的。
2.3挡土墙变形对于土体变形的影响
图10,11给出了加支撑情况下墙后土体的水平变形和开挖面下的变形,同时对比不加支撑情况可[CM)][LL][LL]得:①加支撑影响范围大约在12 m深度内,不加支撑影响范围大约在18 m深度内,加支撑在缩小对土体变形影响范围上有很明显的效果,距离挡土墙4 m左右时对土体变形的影响是最严重的,不加支撑时挡土墙中部范围有一个危险区域,加支撑后对墙后土体的变形有一定分散减小的效果;②基坑开挖深度为9 m,2个影响范围都在2倍开挖深度以内,所以假设的模型土体的影响范围是偏于安全的。对竖向变形的影响,加支撑和不加支撑影响范围为开挖面以下约18 m和15 m深度的范圍,也在2倍开挖深度范围以内,所以2倍开挖深度是基坑变形大致的影响范围。支撑的作用只能限制对于水平方向变形的影响范围,而对于深度方向的变形影响作用并不大。
2.4主被动区土压力分布及其分析
表3给出了不同截面开挖深度处的土压力。由于基坑受到对称荷载,数据近似对称,所以取1/4基坑数据进行分析。主动土压力区同一深度处基坑的应力变化是从坑角处最大值减小到基坑中部“马鞍”状分布,随着基坑深度的增加,应力值逐渐增加。被动区上部土体被移除,竖向荷载减小,因此水平向的压力减小,但是由于挡土结构的变形作用使挡土墙产生挤土作用,土体的有效内摩擦角增大,抗剪强度随之提高,因此被动区的土压力值在开挖面附近并不是从0开始而是要比理论值高。被动区的土压力分布和位移的分布规律类似:基坑边角的土压力最小,在向基坑中部分布的过程中,土压力值逐渐增加。对三维土压力和平面土压力进行对比,主被动区的三维土压力模拟值要大于同等平面土压力值,被动区三维土压力要小于同等平面土压力值。对比文献[2]的主动区和被动区的土压力分布规律得到了近似的规律,但是本文施加荷载对于挡土墙的挤土作用更加明显,所以在开挖面处得到的被动区土压力更大一些,同时得到主动区土压力数据在从挡土墙边缘处到中部变化时有一定的反弹,与文献[2]研究得到的逐级递减规律并不相同,并在不加支撑的对照组出现了同样的规律,分析原因:本文取的数据点较密,而文献[2]数据点较为稀疏,可能遗漏了反弹部位数据。
2.5典型位置应力分析
图12给出了加支撑的挡土结构后土体的1/5H,2/5H,3/5H深度处土压力的分布规律。文献[5]中图10的桩身最大负弯矩沿着基坑边的分布规律是从基坑边到一定范围内逐渐降低然后平缓,本文的大致分布规律和文献[5]中给出的结果相近,都是从边缘到中部有一个下降趋势,但是略有不同:挡土墙边缘到挡土墙中部,土压力是从最大值逐渐减小,有一个小范围的上升趋势,并不是完全到达挡土墙中部时土压力最小,而是距离挡土墙5 m左右位置达到最小值,这个范围应该是坑角效应最大影响范围。坑角效应的影响范围前人已有一定的计算[19],并给出了基坑空间效应影响范围的计算公式,近似影响范围b1=Hcot(45°-φ/2),根据计算得本文基坑影响范围为11.7 m。由图10可以看出,在沿挡土墙10 m左右位置到30 m左右位置的土压力分布平缓,近似二维分布规律,本文研究成果符合现阶段研究的结果。
上部是一个抛物线柱体,下部是楔形体。在挡土墙上部同一高度,作用在挡土墙的土压力合力即为主动区土压力,曲线都是抛物线状,土压力是结构空间效应的限制作用和墙后滑裂体土体同时作用的结果,滑裂体性状为抛物线状。土压力的最小值并没有出现在挡土结构的中间部位,中部的土压力又有一定程度的增加。开挖面以下的挡土墙土压力合力是主动区土压力和被动区土压力共同作用的结果,显示在三维位移图上时并没有一个扭曲的变形量,而是近似一个平面形状,这与前人的研究成果相吻合,即下部的滑裂体是一个楔形体契合[20]。
2.6典型位置位移分析
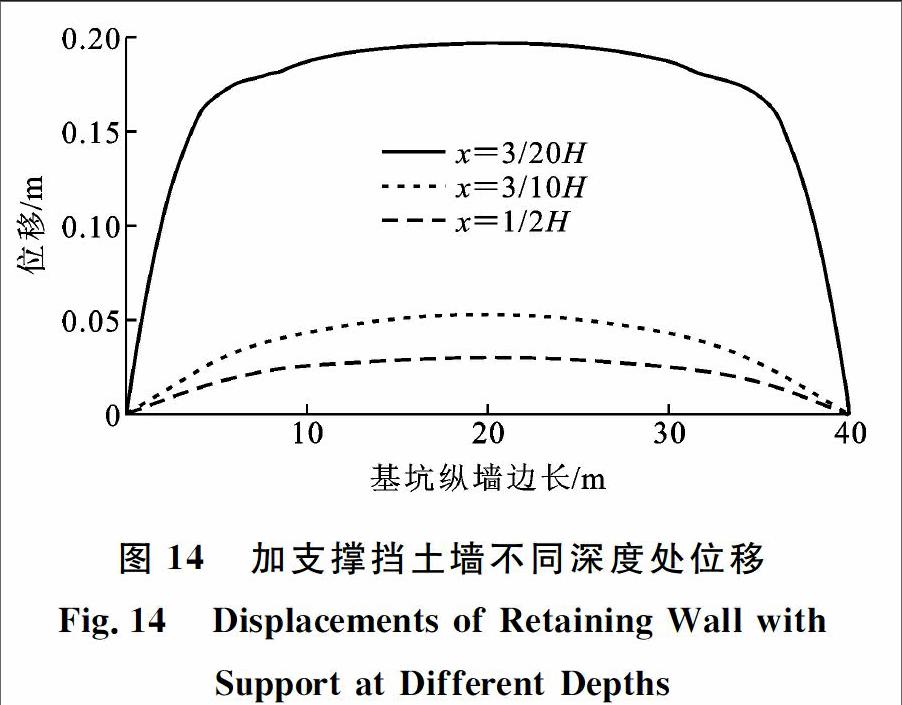
图14给出加支撑的挡土结构后土体不同深度(3/20H,3/10H,1/2H)处位移变化规律。由图14可知,顶部的位移由于支撑的限制作用曲率较小,近似于平面变化,同样,3条曲线的变化规律都符合位移值在主动区的坑角处位移最小、中部最大的规律,与主动土压力分布规律相反。
图15给出了加支撑和不加支撑的顶部位移对比情况。由图15可知,顶部加支撑对于挡土墙中部的位移分布影响很大,顶部不加支撑时,位移值过大,挡土墙在荷载作用下不利于其安全,加支撑后,最大位移值缩小到了很小值,最大位移处出现在挡土墙中部位置,使得整体挡土墙的位移值更加均匀,也使得挡土墙受力更加均匀,这有利于对挡土结构的保护作用。
挡土墙水平位移变化曲线。对比加支撑和不加支撑2种情况可以看出,加支撑和不加支撑对挡土墙的位移影响很大,都呈现的是非线性变化规律,加支撑后沿高度方向位移变化很小,但最顶端的位移还是相对较大,不加支撑的挡土墙沿高度方向变化较为均匀。由于入土深度的加大,加支撑和不加支撑的位移值都近似为0。
3结语
(1)对考虑空间效应的三维主动区土压力分布状况和规律进行了研究。“单片墙”主动区土压力的分布规律是呈“马鞍”状分布:在靠近基坑边缘处主动区土压力达最大值,然后逐渐减小,在靠近挡土墙中部位置处土压力有一定的反弹。被动区土压力和挡土结构的位移情况类似,都是沿着挡土结构从基坑边缘到基坑中部逐渐增大。
(2)挡土结构三维变形对于挡土结构后的土体和挡土结构下部土体的影响符合如下规律:对墙后土体和挡土结构下部土体的影响范围都是近似2倍开挖深度,与文献[11]结论相符。所得影响范围对于工程实际有一定的指导作用。
(3)支撑对于挡土结构的作用十分明显,有效地限制了挡土结构的位移和挡土结构上的土压力,更加近似于平面土压力形式;支撑对限制挡土结构后土体的影响范围有很大效果,极大地限制了墙后土体危险区域的范围,但是对墙下土体的限制作用并不是很明显。在实际工程应用过程中应根据实际需要设置支撑形式以达到防治挡土墙过大变形和防护墙后土体危险区域的作用。
(4)“单片墙”空间效应影响范围在竖直方向为开挖深度2倍左右,但是墙后土体的变形影响最大范围约为1/2开挖深度。
(5)由于坑角效应影响和滑裂体对挡土结构共同作用的结果,土压力最小值出现在坑角效应影响范围内一半位置处。因本文研究深度有限,并没有深入探究具体的影响机制,做如下假设和分析:无论墙后土压力的分布规律是“凹”的抛物线还是“凸”的抛物线,挡土墙挠度分布都是中间大和两边小的规律;挡土墙角部位置简化为固支结构更加符合挡土墙角部应力最大的规律。
(6)本文对于土压力的分布数据只是做出规律性的分析和对比,并没有给出具体的土压力分布公式,还需要进行更深一步的研究并总结。
參考文献:
[1] 杨雪强,刘祖德,何世秀.论深基坑支护的空间效应[J].岩土工程学报,1998,20(2):74-78.
YANG Xue-qiang,LIU Zu-de,HE Shi-xiu.Research About Spatial Effect of Deep Pit Supporting[J].Chinese Journal of Geotechnical Engineering,1998,20(2):74-78.
[2]俞建霖,龚晓南.深基坑工程的空间性状分析[J].岩土工程学报,1999,21(1):21-25.
YU Jian-lin,GONG Xiao-nan.Spatial Behavior Analysis of Deep Excavation[J].Chinese Journal of Geotechnical Engineering,1999,21(1):21-25.
[3]SIMPSON B.Retaining Structures:Displacement and Design[J].Géotechnique,1992,42(4):541-576.
[4]LEE F K,YONG K Y,QUAN K C N,et al.Effect of Corners in Strutted Excavations:Field Monitoring and Case Histories[J].Journal of Geotechnical & Geoenvironmental Engineering,1998,124(4):339-349.
[5]陈页开,徐日庆,任 超,等.基坑开挖的空间效应分析[J].建筑结构,2001,31(10):42-44.
CHEN Ye-kai,XU Ri-qing,REN Chao,et al.Spatial Effect Analysis of a Pit Excavation[J].Building Structure,2001,31(10):42-44.
[6]崔春义,李顺群,栾茂田,等.基于ABAQUS的连续墙支护深基坑开挖弹塑性数值分析[J].岩土工程学报,2008,30(增):86-90.
CUI Chun-yi,LI Shun-qun,LUAN Mao-tian,et al.Numerical Elasto-plastic Analysis of Deep Foundation Pit Excavation with Bracing Diaphragm Walls[J].Chinese Journal of Geotechnical Engineering,2008,30(S):86-90.
[7]卢坤林,杨 扬.考虑位移影响的主动土压力近似计算方法[J].岩土力学,2009,30(2):553-557.
LU Kun-lin,YANG Yang.Approximate Calculation Method of Active Earth Pressure Considering Displacement[J].Rock and Soil Mechanics,2009,30(2):553-557.
[8]黄亚娟,赵均海,田文秀.基于双剪统一强度理论的刚性结构物竖直土压力计算[J].建筑科学与工程学报,2008,25(1):107-110.
HUANG Ya-juan,ZHAO Jun-hai,TIAN Wen-xiu.Calculation of Vertical Earth Pressure of Rigidity Structures Based on Two Shear Unified Strength Theory[J].Journal of Architecture and Civil Engineering,2008,25(1):107-110.
[9]贾 萍,赵均海,魏雪英,等.空间主动土压力双剪统一解的简化计算[J].建筑科学与工程学报,2008,25(2):85-89.
JIA Ping,ZHAO Jun-hai,WEI Xue-ying,et al.Simplified Calculation of Twin-shear Unified Solution of Space Active Earth Pressure[J].Journal of Architecture and Civil Engineering,2008,25(2):85-89.
[10]BONO N A,LIU T K,SOYDEMIR C.Performance of an Internally Braced Slurry.Diaphragm Wall for Excavation Support[C]//PAUL D B,DAVIDSON R R,CAVALLI N J.Slurry Wall:Design,Construction and Quality Control(STP 1129).Philadelphia:ASTM,1992:347-360.
[11]趙利益,蔡伟铭.深基坑开挖三维弹塑性有限元分析[J].上海铁道大学学报:自然科学版,1997,18(4):100-105.
ZHAO Li-yi,CAI Wei-ming.3-dimension Elastic-plastic Finite Element Analysis of the Deep Foundation Pit Excavation[J].Journal of Shanghai Tiedao University:Natural Science,1997,18(4):100-105.
[12]刘小丽,吕大镛,窦远明,等.基坑开挖的三维弹塑性有限元模拟[J].河北工业大学学报,2000,29(5):92-96.
LIU Xiao-li,LU Da-yong,DOU Yuan-ming,et al.Simulating of an Actual Foundation Pit Excavation with Three-dimensional Elastic-plastic Finite Element Method[J].Journal of Hebei University of Technology,2000,29(5):92-96.
[13]程祖锋,师欢欢,徐光兵.基于ABAQUS的深基坑变形和内力三维有限元分析[J].煤炭工程,2013(9):119-121.
CHENG Zu-feng,SHI Huan-huan,XU Guang-bing.Three Dimensional Finite Element Analysis of Deformation and Internal Forces of Deep Foundation Pit[J].Coal Engineering,2013(9):119-121.
[14]林 鹏.基于板桩墙支护的基坑开挖模型试验的三维数值分析及变形预测[D].南昌:华东交通大学,2008.
LIN Peng.Based on 3D Numerical Analysis of the Sheet Pile Wall Supporting Model and Deformation Predicting for Deep Foundation Pit[D].Nanchang:East China Jiaotong University,2008.
[15]潘 锋,王国体.柔性支护深基坑工程中土压力的有限元模拟[J].工程与建设,2009,23(5):690-692.
PAN Feng,WANG Guo-ti.Finite Element Simulation of Earth Pressure in Deep Excavation[J].Engineering and Construction,2009,23(5):690-692.
[16]OU C Y,CHIOU D C.Three Dimensional Finite Element Analysis of Deep Excavations[J].Journal of the Geotechnical Engineering,1996,122(5):337-345.
[17]贾 堤,石 峰,郑 刚,等.深基坑工程数值模拟土体弹性模量取值的探讨[J].岩土工程学报,2008,30(增):155-158.
JIA Di,SHI Feng,ZHENG Gang,et al.Elastic Modulus of Soil Used in Numerical Simulation of Deep Foundation Pits[J].Chinese Journal of Geotechnical Engineering,2008,30(S):155-158.
[18]宋二祥,娄 鹏,陆新征,等.某特深基坑支护的非线性三维有限元分析[J].岩土力学,2004,25(4):538-543.
SONG Er-xiang,LOU Peng,LU Xin-zheng,et al.Nonlinear 3D Finite Element Analysis of an Extremely Deep Excavation Support System[J].Rock and Soil Mechanics,2004,25(4):538-543.
[19]顾慰慈.挡土墙土压力计算[M].北京:中国建材工业出版社,2001.
GU Wei-ci.Calculation of Earth Pressure on Retaining Wall[M].Beijing:China Building Materials Industry Press,2001.
[20]黄 强.护坡桩空间受力简化计算方法[J].建筑技术,1989(6):43-45.
HUANG Qiang.Simplified Calculation Method of Space Stress of Slope Protection Pile[J].Architecture Technology,1989(6):43-45.

