Farkas引理的一种新的证明
钱金娥
(长江大学 信息与数学学院,湖北 荆州 434023)
Farkas引理的一种新的证明
钱金娥
(长江大学 信息与数学学院,湖北 荆州 434023)
关于Farkas引理的证明有很多种不同的方法,主要包括三类:初等证明,代数证明和几何证明.而本文中给出了其中的一类方法,属于初等证明.
Farkas引理;初等证明;有效集法
1 前言
Farkas引理是一个经典的结果,是最优化方法中最为基础的工具之一.该引理首次由Farkas于1902年提出.我们可以在大多数最优化教程中发现该引理的证明,如文献[2]中.这个引理的早期证明类似于对偶单纯形法,但其证明并未考虑到可能出现的循环现象,因此并不完整.近期的证明通常基于凸集分离定理.这种方法有一个简单和更直观的几何解释,参见文献[10].在本文中我们试图克服这个困难通过一个简单展示一个简单的独立的证据是基于基本的论据.
2 Farkas引理
设A是m×n实矩阵,c为非零的n维常向量.Farkas引理声称对于如下两个系统:
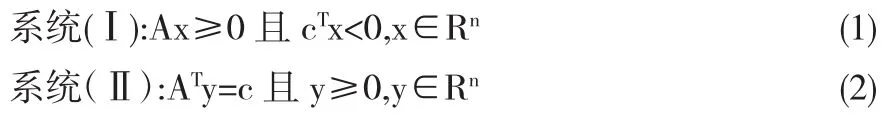
不能同时都有解.
注意,cTx<0意味着x≠0;ATy=c意味着y≠0.(零向量的维数与对应向量维数相匹配.)如果系统(1)、(2)满足不等式:
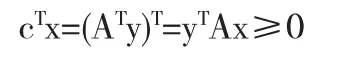
与cTx<0矛盾.因此,两个系统都有解是不可能的.两个系统都可解的问题又可以通过考虑约束最小二乘问题来回答:

这里|| ||表示欧几里得范数.
令y*是Rm中给定的一点,令

表示相应的余向量.我们将证明,由下面的引理2,y*为(3)式的解,当且仅当y*和r*满足下列条件:

这些条件下面还会被用在建立存在一点y*∈Rm为 (3)式的解.
结合(4)、(5)可得:
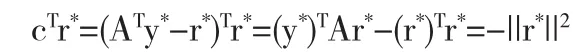
由此我们将得出以下结论.
定理1 令y*为方程(3)的解,令r*=ATy*-c,表示相应的余向量.如果r*=0,y*为(2)的解.否则,r*为(1)的解,cTr*=-||r*||2.
引理2 令y*=(y1*,…,ym*)T是Rm中给定的一点,令r*由(4)定义,因此,y*为(3)的解,当且仅当y*、r*满足(5).
证明 假设y*为(3)的解,考虑单参数求积函数
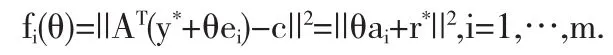
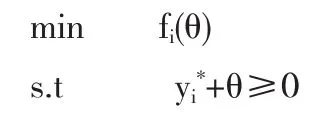
由此得到(5).
相反地,假设(5)有效,令z为Rm中的任意点,有z≥0,令m维向量u=(u1,…,um)T由z的性质可知u=z-y*,因此,yi*=0意味着ui≥0,可得uTAr*≥0.
因此,由恒等式:
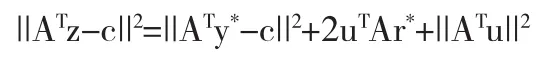
可以得到||ATz-c||2≥||ATy*-c||2.则需要建立存在一个点y*为(3)的解.
上述定理可以由一个简单的迭代运算完成需要k次迭代,k=1,2,….具体实现由以下两个步骤组成.
第一步:解决一个不受约束的最小二乘问题.
若t=0或rk=0,则跳到第二步.
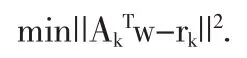
注意到0为此问题的解.当且仅当Akrk=0.在这种情况下,跳到第二步.定义一个非零搜索方向由分量为ui=wi,i=1,…,t和ui=0,i=t+1,…,m.记号和则下一点被定义为y(k+1)=u(k)+θku(k),其中θk>0为区间[0,1]中的最大数保持点y(k)+θu(k)对上述问题可行.换句话说,θk是区间{1}∪中的最小数.
第二步:测试最佳性和远离无意义的点,这里有Akrk=0,则意味着y(k)为以下问题的解:
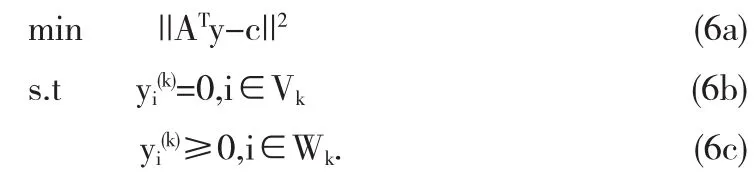
在这种情况下,y(k)被称为“无意义点”,为测试y(k)是否为最佳的,我们估算指数j为
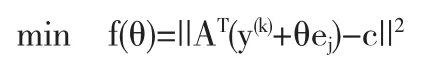
的最优解.
上述运算具有有限终止属性,同时有如下结果:
(a)在每个迭代中,目标函数是严格递减的,即
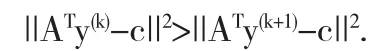
(b)对上述提到的θk有0≤θk≤1.则有,如果θk=1,则y(k+1)是无意义的点.否则,当0<θk<1,t递减.因此,这是不可能的去完成超过m次迭代而不到达无意义点.
(c)我们每次到达一个无意义的点,当前的点y(k)为(6)式的解.
(d)对这些问题的数量是有限的,然而,由于存在(6a)式,故访问同样的问题(6)两次是不可能的.
上述迭代过程本质上属于有效集法.有效集是指那些在最优点有效的不等式约束所组成的集合.如果我们能提前知道在最优点处有效的约束,那我们就可以把那些未有效的不等式约束剔除掉并把原命题转化成更易求解的等式约束命题.然而,在求解之前我们往往对最优点处的有效约束知之甚少.因此如何找到最优点处的有效约束也就是有效集法的主要工作.
将新的证明方法与其他的方法相比而言是有趣的.一个传统的方法去证明点y*为(3)式的解的存在性是在观察Z= {ATy|y≥0}为Rn上的闭集的基础上的.
证明这一要求的确要详细的阐述.如[2,P.332-334]或[8, P.10].利用闭集Z,可得B={z|z∈Z,||z-c||≤||c||}是Rm上的一个非空的闭集.同时注意:φ(x)=||x-c||2是x的一个连续函数.因此,由魏尔施特拉斯定理,φ(x)可得出它的最小值在B上.令z*∈B表示最小值点.若B⊆Z,则存在一点y*∈Rm,使y*≥0和z*=ATy*;因此,y*为(3)式的解.点z*=ATy*是c在Z上的映射.若Z是一个凸集,φ(x)是一个严格凸函数,z*是唯一的.然而,y*不是唯一的. 这一特征与r*性质密切相关,虽然众所周知,但是通常注意较少[4].
推论3 令y*和r*同定理1中所定义的,假设r*≠0,则向量r*/||r*||为最速下降问题的解:
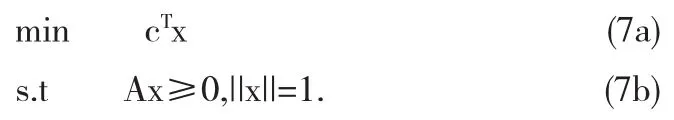
证明 令x满足约束条件(7b),则(y*)TAx≥0,由柯西-施瓦兹不等式有:
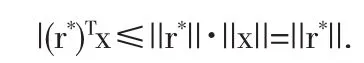
综上所述有:
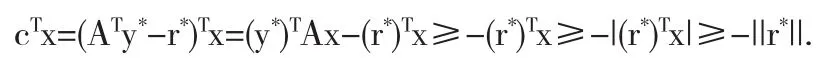
因此,cTr*/||r*||=-||r*||,即得证.
证明Farkas引理的一种常见方法是应用分离超平面定理,参见文献[2,3,4,5,6,7].这个方法需要运用分离超平面定理和闭集Z,c为Z上一个映射.在我们的证明中,定理1代替分离超平面定理,前面两个步骤给出的本质上是有效集法,而y*则是通过一个典型的“有效集”的方法得出的.因此,这种相似的证明方法也能在其他的定理中使用.例如最小二乘问题结合最速下降方向,能够计算出最速下降法为解决有效集方法退化提供了一种有效的方法,这个问题在参考文献[2]中有详细的讨论.
〔1〕AChiya Dax.An Elementary proof of Farkas’Lemma*. 39(3)(1997),pp.503-507,September.
〔2〕P.G.Ciarlet,Introduction to Numerical Linear Algebra and Optimization,Cambridge university Press,Cambridge, 1989.
〔3〕P.E.Gill,W Murray,and M.H.Wright,Numerical Linear and Optimization,1(1991),Addison-Wesley Reading,MA,.
〔4〕M.J.D.Powell,Introduction to Constrained Optimization, in Numerical Methods for Constrained Optimization,P. E.Gill and Wurray,eds.,Academic Press,New York,(1970), pp.1-28,.
〔5〕R.Fletcher,Practical Methods of Optimization.2(1981): Constrained Optimization,John.Wiley,New York.
〔6〕G.P.McComick,Nonlinear Programming,McGraw-Hill, New York,(1969).
〔7〕G.Zoutendijk,Methods of Feasible Directions,Elsevier-North Holland,Amsterdam,(1960).
〔8〕M.R.Osborne,Finite Algorithms in Optimization and Data Analysis,John.Wiley&Sons,Chichester,(1985).
〔9〕A.DAX,The relationship between theorems of the alternation,least norm descent directions,And degeneracy:A review,Ann.Oper.Res.,46(1993),pp.11-60.
〔10〕Yuan Y X,Sun W Y.Optimization Theory and Algorithms.Beijing:Science Press,(1997).
O221
A
1673-260X(2017)03-0001-02
2016-11-21

