近井筒分支缝起裂形成机制研究

李秀钊，郑一鸣

(中石油燃料油有限责任公司青岛仓储分公司，山东 青岛 266500)

近井筒分支缝起裂形成机制研究

李秀钊，郑一鸣

(中石油燃料油有限责任公司青岛仓储分公司，山东 青岛 266500)

针对多分支缝水力压裂井筒起裂问题，从弹性力学的理论方向出发，在考虑初次压裂诱导应力对近井地带应力场的作用下，建立多分支缝起裂、起裂角及起裂压力的力学模型。在此模型的基础上，通过编制计算机程序的方法，计算分析多分支缝起裂的影响因素。研究表明，低水平应力差及高闭合应力条件下，所形成分支缝的起裂角度大，分支缝水力压裂效果好；初始缝长度也是分支缝起裂的影响因素之一，在低水平应力差、初始裂缝缝长短的条件下，分支缝偏转程度高，更易重新定向；对比7口井分支缝的力学模型起裂压力及现场施工起裂压力，验证了模型的准确性。研究成果对多分支缝水力压裂工艺提供了理论基础并且一定程度上指导现场作业，优化分支缝压裂的效果。

多分支缝；水力压裂；力学模型；影响因素；现场优化

水力压裂作为低渗储层开发的主要方式之一，一直被油气田开发广泛采用。常规压裂工艺(重复压裂、转向压裂、多裂缝压裂[1～4]等)技术针对性不强，例如海拉尔油田进行常规水力压裂后仍然存在注水井注入难、油井产量衰减快等问题。

针对海拉尔油田低产井压裂后人工裂缝泄油面积有限的问题，实施了多分支缝水力压裂工艺。多分支缝水力压裂是指一次压裂施工、多条主裂缝从井筒起裂，同时每条主裂缝又形成多条次级裂缝的压裂方法。多分支缝水力压裂可以有效地增大近井地带的泄油面积，长期增加产量。不仅适用于低渗储层，常规地层进行水力压裂也可广泛推广。相比较重复压裂，多分支缝水力压裂的特点不仅保证了压裂效果，同时减小相对施工时间，减少了施工材料使用，不仅经济而且环保[5～7]。

多分支缝水力压裂在海拉尔油田部分井位已经成功进行了现场试验，压后单井大幅增产。但是由于压裂工艺的特殊，暂堵后井周围应力场改变，无法预测二次压裂井筒起裂的起裂方向以及近井筒地带的延伸情况。二次压裂起裂角与初次裂缝夹角越大(接近90°)压裂效果越好，裂缝波及体积越大，泄油面积越大。笔者通过计算二次压裂前井筒周围应力场分布，推导了多分支缝水力压裂二次井筒起裂的力学模型，并且在该力学模型的基础上做了一系列的多分支缝起裂影响因素分析[8]。

1 多分支缝起裂力学模型

考虑水平地应力、井底流压、流体径向渗滤等因素的影响，井眼周围地应力分布为[9,10]:

(1)

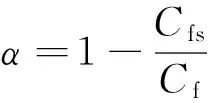
初次压裂后，由于初次压裂裂缝的存在，在初次压裂裂缝诱导应力作用下，井眼周围的诱导应力模型假设为无限大地层中存在一条对称双翼垂直人工裂缝，俯视可以简化为如图1所示物理模型:无限大平板中央存在一条直线裂缝，缝长为2c，裂纹穿透板厚。

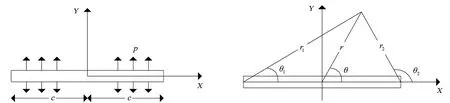
图1 初次裂缝诱导应力场物理模型

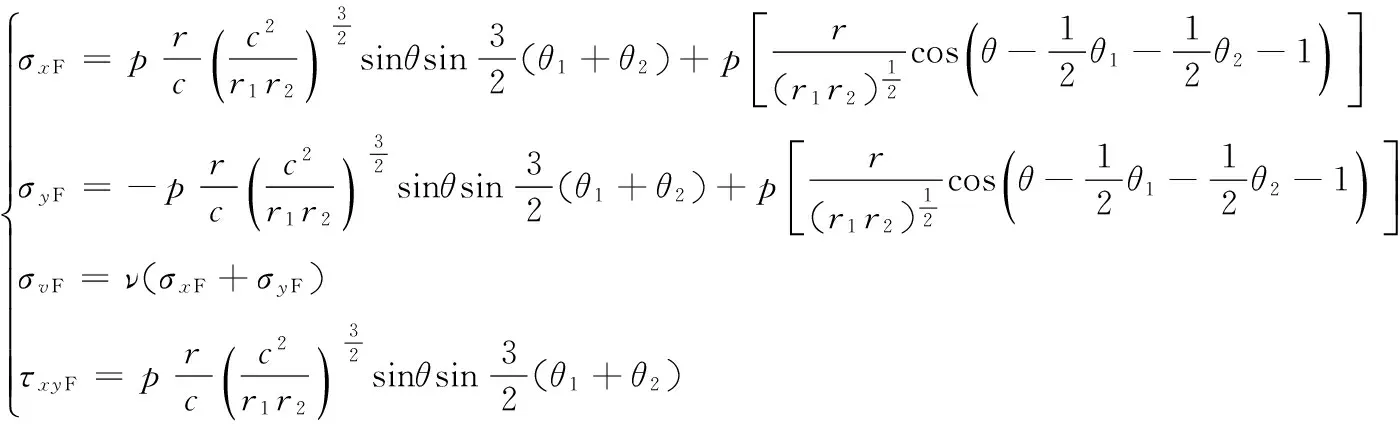
(2)

初次压裂投球后，封堵初次裂缝，缝内静压力p如下式表示:

p=σh-pp

(3)

式中:σxF、σyF、σvF分别为X、Y、V方向的诱导应力，MPa；τxyF为切应力，MPa；r1、r2分别为地层中某一点距裂缝端部的距离，m。

故二次压裂前在初次诱导应力的作用下，井筒周围主应力分布为:

(4)

将式(2)、(3)、(4)代入到式(1)得到二次压裂前井筒周围应力场。井筒周围周向应力表示为:

(5)

井壁上存在的有效周向应力达到或超过井壁岩石水平方向的抗拉强度时，在垂直于水平周向应力的方向上产生垂直裂缝，即:

-σθ≤σt

(6)

因此随着注入压力增大-σθ最大的点即为裂缝起裂点，由于诱导应力的存在，裂缝不会沿最大主应力方向延伸，θ即为裂缝初始偏转角。θ越接近90°，分支缝压裂效果越好。由下式可以计算出分支缝的偏转角:

(7)

在考虑射孔的条件下，假设射孔范围包括裂缝偏转角方向，由于初次压裂诱导应力的存在，孔眼顶部的周向应力大于孔眼根部的周向应力，所以二次压裂将从射孔孔眼顶部起裂，取r值为射孔平均深度。

射孔完井方式压裂条件下，孔壁上任意一点的周向应力分布为:

(8)

将式(7)计算出的起裂角代入到式(8)即可计算出分支缝的起裂压力pf。

2 多分支井筒起裂影响因素及分析

2.1 影响分支缝起裂角的因素

计算基本参数:垂向应力为25MPa，孔隙压力10MPa，泊松比为0.25，射孔平均长度为2m，孔眼半径取5.5cm，Biot常数为0.6。

编制计算机程序计算分支缝起裂角的影响因素，如图2、3、4所示。

图2 起裂角随水平应力差变化曲线 图3 起裂角随初始裂缝半长变化曲线

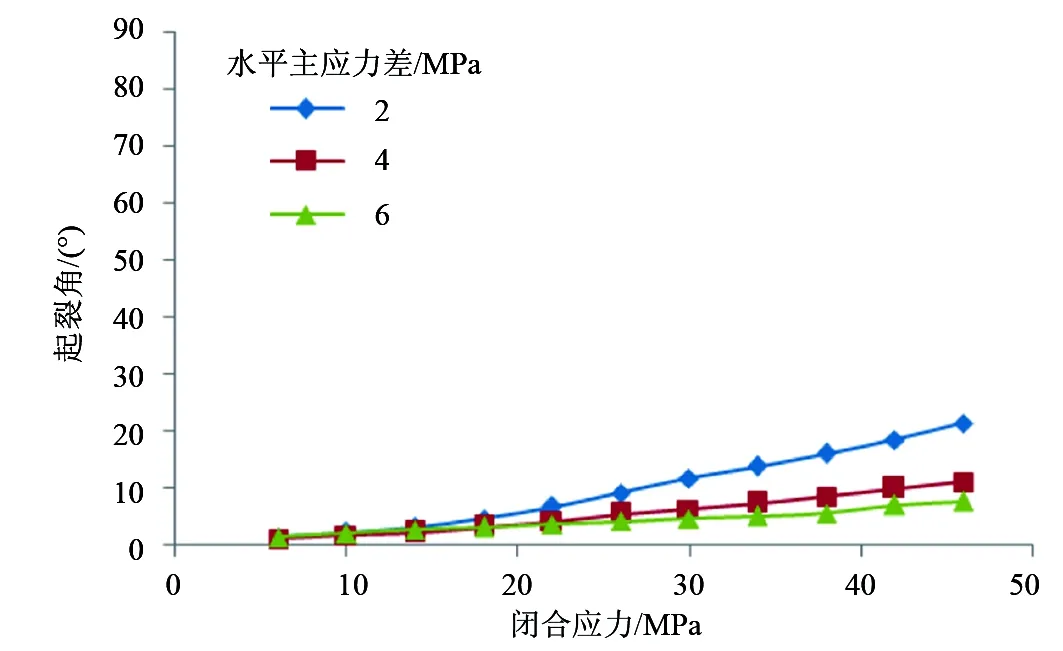
图4 起裂角随闭合应力变化曲线

图2为在初始裂缝半长为30、40、50m情况下起裂角随水平应力差的变化情况，可以看出随着水平应力差的增大，分支缝起裂角在变小，应力差在2MPa以内时，起裂角变化敏感，当应力差增大到6MPa时，起裂角接近0°。图3为水平主应力差分别为2、4、6MPa时，分支缝起裂角随初始裂缝半长的变化情况，初始裂缝半长越大，分支缝起裂角越小；相比较于水平应力差分支缝起裂角对初始裂缝半长的敏感程度较低。图4为水平主应力差分别为2、4、6MPa的条件下，起裂角随闭合应力的变化情况，初始裂缝闭合应力可以理解为水平最小主应力，可以看出闭合应力越大，分支缝起裂角越大，但即使闭合应力增大到46MPa，起裂角增加也不明显，由此可以认为，闭合应力对分支裂缝起裂方向有一定影响，但影响不大。

在初始裂缝诱导应力的作用下，井筒周围地应力存在一定程度的变化，应力差越小，地应力变化越明显；由于诱导应力是初始裂缝尖端集中应力产生的，因此初始裂缝长度越长，诱导应力对井筒的作用就越薄弱；闭合应力大小直接关系到缝内静压力的大小，决定了诱导应力的大小，因此闭合应力也是分支缝起裂方向的影响因素之一。

2.2 近井筒地带分支缝延伸形态分析

井筒起裂的分支缝在近井筒地带的延伸方向直接影响压裂后裂缝与油层的接触面积。在诱导应力的作用下，近井筒地带地应力随着距井筒中心半径增大，应力集中点也随之变化。产生裂缝后，裂缝沿最大周向应力方向延伸，随着裂缝的延伸，虽然裂缝尖端点未必是距井筒相同半径内最大周向应力点，但裂缝必然会朝着最大周向应力点方向延伸，故通过分析近井地带不同半径最大周向应力方向，可以分析出不同情况下分支缝延伸形态[9～12]。

图5为不同应力差条件下，近井筒地带最大周向应力方向的变化情况。当ΔH=2MPa时，在距井筒9m范围内最大周向应力方向达到90°，应力差越大，最大周向应力方向变化越慢，裂缝延伸偏转程度越低。图6为不同初始裂缝半长条件下，近井筒地带最大周向应力的变化情况。在初始裂缝半长为30m条件下，距井筒中心距离7m范围，最大周向应力方向就变为90°，可以看出初始裂缝长度对近井筒地带的地应力重新定向起着重要作用。由图7可以推断裂缝的延伸情况[13～15]。可以看出应力差越低，初始裂缝延伸程度低的条件下，分支缝压裂效果好，反之效果相对较差。

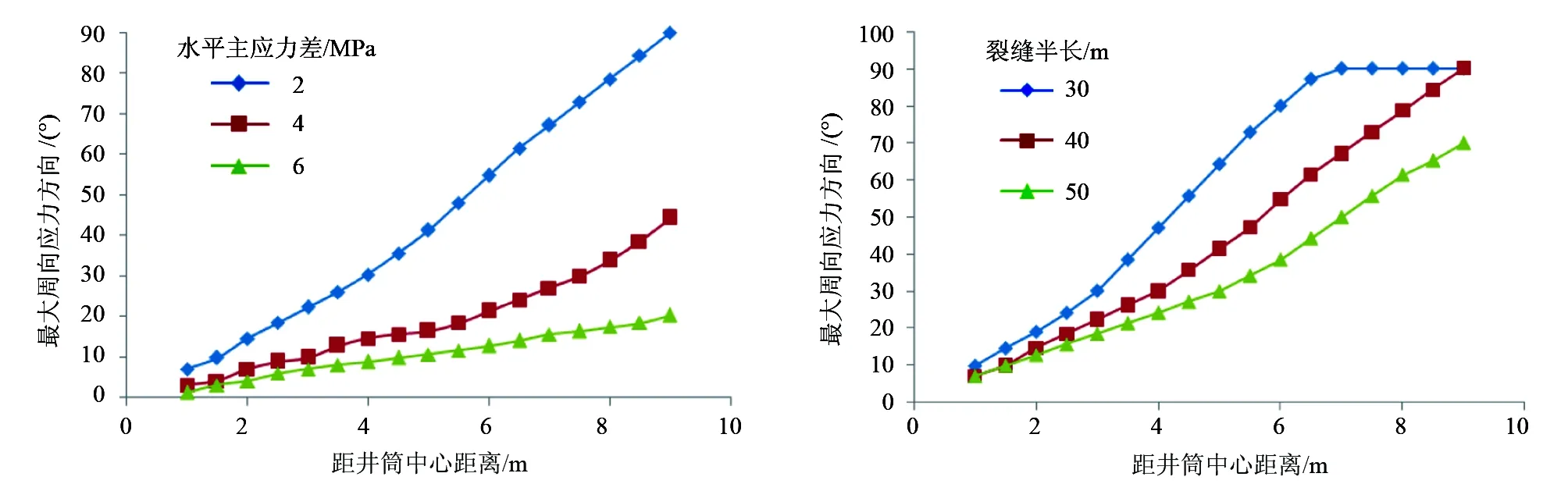
图5 不同水平主应力差下，近井地带 图6 不同初始裂缝半长下，近井地带 最大周向应力方向变化情况 最大周向应力方向变化情况

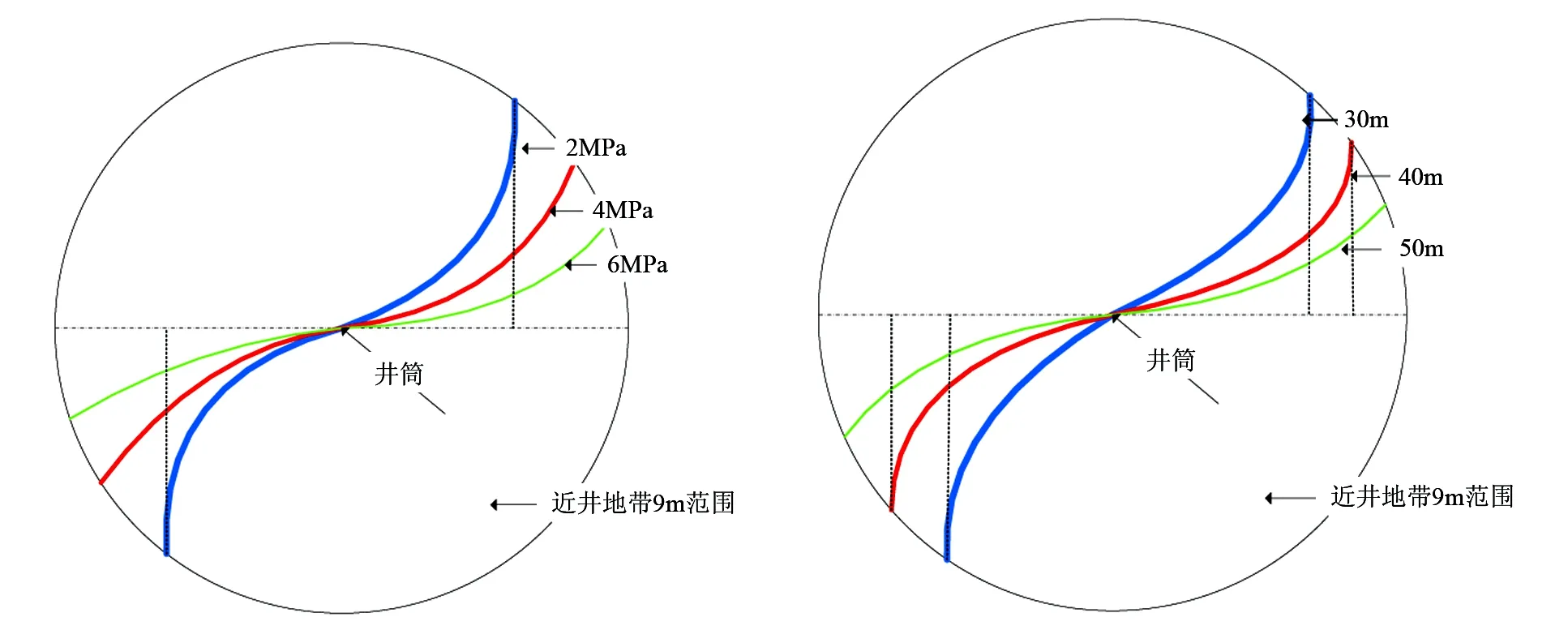
图7 近井地带分支缝延伸趋势图

3 现场结果及分析

以贝62-61井为例，其主压裂施工曲线如图8所示。贝62-61井在压裂55min时注入暂堵剂，压力上升至24.4MPa，地层发生二次破裂，说明该井近井筒多分支缝水力压裂成功。

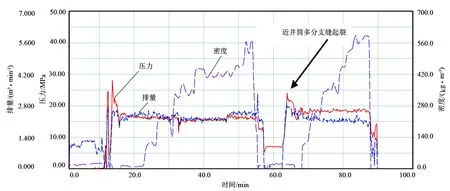
图8 贝62-61井主压裂施工曲线

井号实测破裂压力/MPa计算破裂压力/MPa误差/%贝62-6124.425.64.92乌105-9539.140.33.07贝28-x62-5829.632.710.47贝28-X62-6027.128.55.17贝28-X58-5426.727.11.50希47-3846.246.50.65贝28-X58-5626.828.87.46

根据现场7口井的实际地质情况，按照式(6)～(8)计算出破裂压力和实际的分支缝破裂压力。7口井的计算结果如表1所示，计算的破裂压力整体都高于现场实际情况，分析是由于多分支缝水力压裂投球暂堵井筒起裂的施工过程暂堵效果不稳定，考虑天然裂缝存在的条件下，降低了分支缝井口起裂的起裂压力。7口井中贝28-X62-60井、贝28-x62-58井、贝28-X58-56井这3口井的误差率在5%以上，其余4口井分支缝的破裂压力在5%以内，说明该文的分支缝起裂压力计算公式算出的破裂压力基本合理，符合现场施工情况。

4 结论

1)考虑初始裂缝诱导应力的影响，推导了全堵条件下多分支缝起裂的偏转角及起裂压力力学模型。

2)根据推导的力学模型，分析了原始地应力差、初始裂缝长度及闭合应力对分支缝起裂角的影响，确定了分支缝起裂的主要影响因素。

3)通过分析近井地带最大周向应力方向变化情况，描述了不同应力差及不同初始缝长条件下分支缝的延伸形态，进一步确定分支缝压裂效果好坏的影响因素。

4)根据建立的模型计算出分支缝破裂压力，并和现场7口井的分支缝压裂破裂压力进行对比，验证了模型的准确性和实用性，根据现场地质数据调整初次压裂规模，以优化分支缝压裂效果。

[1]董光，邓金根，朱海燕，等.重复压裂前的地应力场分析[J].断块油气田，2012，19(4):485～488，492.

[2]甘云雁，张士诚，刘书杰，等.整体压裂井网与裂缝优化设计新方法[J].石油学报，2011，32(2):290～294.

[3]李士斌，王昶皓，张立刚.重复压裂裂缝转向机理及储层评价方法[J].断块油气田，2015,21(3):364～367.

[4]姚洪田，周洪亮，窦淑萍，等.低渗透油藏注水井有效压裂技术探索[J].特种油气藏，2014,21(1):127～130.

[5]Sato K，Wright C A，Ichikawa M. Post-frac analyses indicating multiple fractures created in a volcanic formation[J].SPE39513,1998.

[6]罗天雨，赵金洲. 复杂裂缝产生机理研究[J].断块油气田，2008,15(3):46～48.

[7]陈勉, 周健, 金衍, 等. 随机裂缝性储层压裂特征实验研究[J]. 石油学报, 2008, 29(3):431～433.

[8]Chen Yiheng, Hasebe N. A consistency check for strongly interacting multiple crack problems in isotropic, bimaterial and orthotropic bodies[J]. International Journal of Fracture, 1998, 89(4):333～353.

[9]闫铁，李玮，毕雪亮.清水压裂裂缝闭合形态的力学分析[J].岩石力学与工程学报，2009,28(2):3471～3476.

[10]金衍, 陈勉, 周健, 等. 岩性突变体对水力裂缝延伸影响的实验研究[J].石油学报, 2008, 29(2):300～303.

[11]李小波，史英，张修明，等.水力压裂裂缝模拟研究[J].西安石油大学学报(自然科学版)，2009，24(3):52～55.

[12]程远方，徐太双，吴百烈，等.煤岩水力压裂裂缝形态实验研究[J].天然气地球科学，2013，24(1):134～137.

[13]王凤江，丁云宏，路勇.低渗透油田重复压裂技术研究[J].石油勘探与开发，1999，26 (1):71～73.

[14]段银鹿，李倩，姚韦萍，等.水力压裂微地震裂缝监测技术及应用[J].断块油气田，2013,20(5):644～648.

[15]彭通属，刘强，何欣，等.立体裂缝实时监测技术在油藏水力压裂中的应用[J].石油化工高等学校学报,2011，24(3):47～51.

[编辑] 帅群

2016-01-10

李秀钊(1990-)，男，助理工程师，从事钻井工程方面的研究，dingyue.bin@163.com。

TE357

A

1673-1409(2017)3-0065-06

[引著格式]李秀钊，郑一鸣.近井筒分支缝起裂形成机制研究[J].长江大学学报(自科版), 2017,14(3):65～70.