动力系统的平衡点在库存管理方面的应用

刘元姝

(营口职业技术学院 教务处，辽宁 营口 115000)

动力系统的平衡点在库存管理方面的应用

刘元姝

(营口职业技术学院 教务处，辽宁 营口 115000)

库存管理是企业管理中相当重要的一环，企业为了保障市场供应，又不产生过多的库存积压，维持合理和科学的库存量是非常必要的。本文试图把动力系统与企业的库存量结合起来，建立库存管理理论的数学模型，通过对数学模型的分析，从而采取有效的方法来调控商品的库存量。这个模型很容易达成应用程序的编写，进而实施现场的控制，因此具有很高的利用价值。

动力系统；安全库存；平衡点；调控

企业要维持持续健康的发展，就必须保持最佳的库存量，而库存量的高低是众多因素集成的结果，包括市场需求，价格走势，企业库存战略等，其中的市场需求是很难预测的。企业若要利用库存这把“双刃剑”，最根本的出发点就是找到库存量的“平衡点”。本文就是从动力系统的平衡点的角度来讨论企业库存管理的，具有一定的实际意义。

1 库存理论

(1)库存是一个广义的、抽象的概念，在实际的问题中，需要界定库存的具体类别，才不会在沟通中产生误会。

(2)库存按功能可以划分为安全库存、最大库存、平均库存等。安全库存就是为了防备“需求”和“供应”的不确定性，因此，每个企业都要设定自己的安全库存。

(3)库存量主要由市场的需求来决定。但这种需求是很难预测的，在其它条件既定的条件下，将企业的库存看作一个系统，而市场的影响作为一种动力，就形成了库存动力系统。

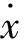
2 动力系统与平衡点

(1)动力系统[2]

定义1S是Rn中的开集，映射φ：R1×S→S，φ连续，记φ(t,x)为φt(x)，固定t时，φt：S→S，满足：

①φ0：S→S是恒等映射。

②φtφs=φt+s对R1内一切t,s都成立。

则称φt为动力系统。

定义2 设φ是Rn上的连续的动力系统，对任意的x0∈Rn，则φ(x0)为以x0为初始值的轨道或流。

(2)平衡点[3]

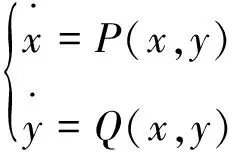
(1)

变换后的方程以(0,0)为平衡点。所以动力系统的平衡点可以转化为原点，本文中讨论的平衡点都为原点。

3 库存动力系统

(1)一维库存动力系统[4]

当m>0时，系统呈指数特性增长，此时的生产量高于需求量，库存量会逐渐的增加，根据m的值，可以预测产品的需求速度，进而减少生产速度,使库存量趋于合理化。当m<0时，系统呈指数特性减少，此时的生产量小于需求量，库存量会逐渐的减少。这时应该增加生产的速度，以达到供需的合理化。

(2)二维库存动力系统

(2)

(3)

当A的特征值都有负的实部时，系统(2)的平衡点是渐进稳定的；两个特征值只要有一个是正实部时，平衡点是不稳定的；换句话说，当A的特征值都有非零实部时，系统(2)在平衡点处的稳定性与其线性近似方程(3)在平衡点(0,0)处的稳定性是一样的。

根据A的特征值和定义3可以来判断相应系统在平衡点附近的性质，进而为系统的调控提供依据。

(3)n维库存动力系统：

n维库存动力系统的情况与二维的情况相似，本文不予讨论。

4 库存动力系统的调控

(1)库存动力系统的分析[5]

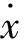
(2)一维库存动力系统的预测与调控：

①记录库存数据：x1,x2,x3…xn

②作散点图，如图1所示。

图1 库存散点图

(3)数据分析

把图1中的数据分成a,b,c,d四部分，如图2所示。

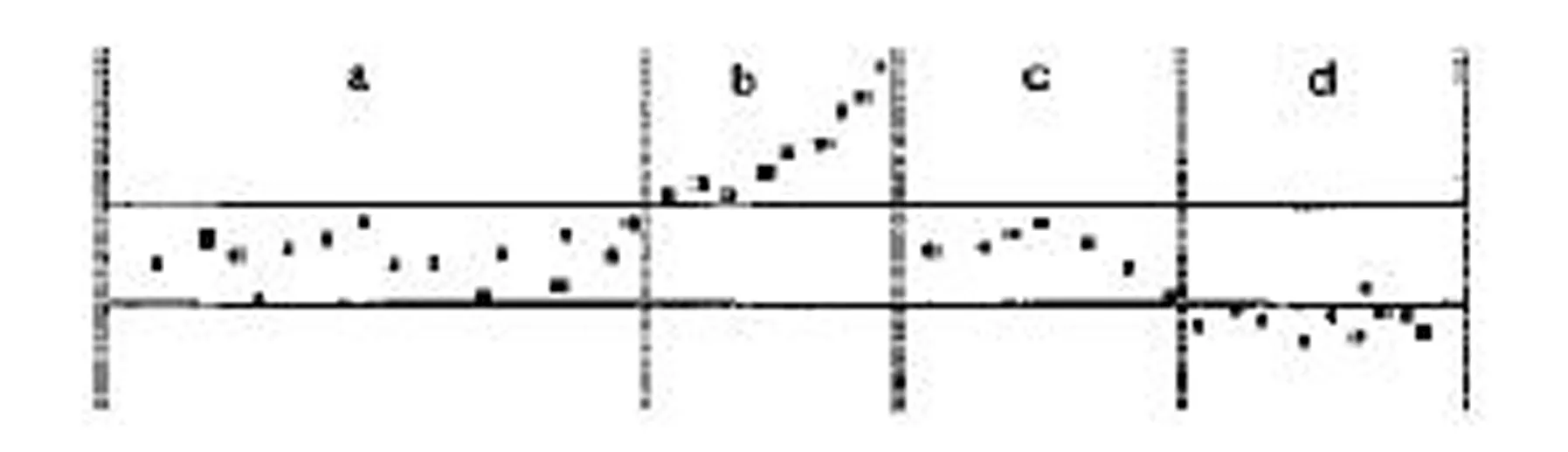
图2 散点分布图

a部分表示比较理想的库存量，企业可以维持原有的生产速度与库存管理策略；b部分超出了安全库存的最大值，并随时间逐步增加，应该根据记录的库存量预测库存系统的数学模型，然后加以调控；c部分与a部分相似，要保持原有的生产速度与库存管理策略；d部分表示超出了预期范围的库存量，但变化平稳，只是生产量与需求量之间存在短缺，应该扩大生产量。

(4)系统的预测与调控

① 预测：这里就b部分进行预测与调控。

**企业**时间记录的库存数据如表1所示。

表1 库存量表(某一时间点) (单位：万件；基本的库存：16)

由表1可得散点图：

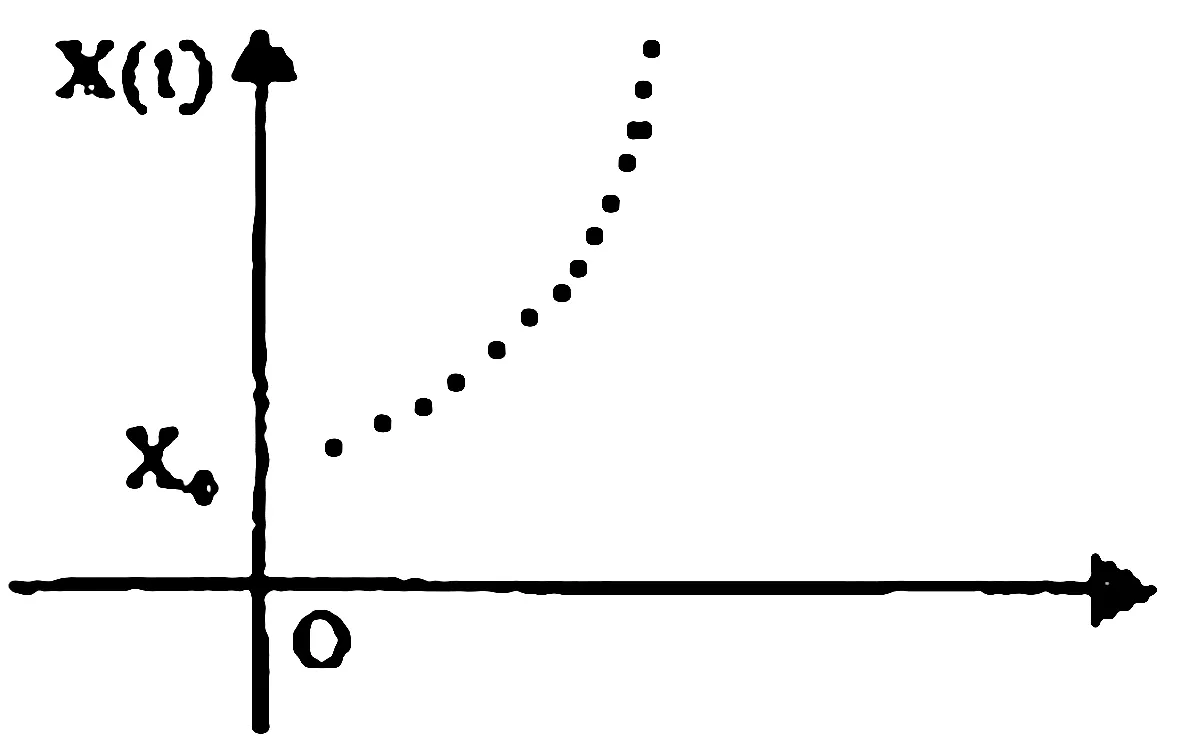
图3 散点图(表1)

(4)

下面我们要确定C,m的值，然后对生产的速度进行调控。

对(4)的两边去对数，令z=lnx，α=m，β=lnC，原式就变为：z=αt+β。原来的表1变为表2。

表2 库存量表(z=lnx)

从表2中可以看出，其中的数据基本满足y=ax+b这个函数的关系。解决这个问题的一般的提法是：以知一组数据：

表3 库存量表(对应关系)

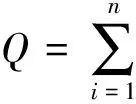
就得到线性方程组：

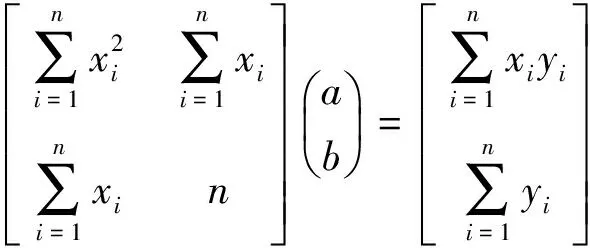
解这个方程组，得到：

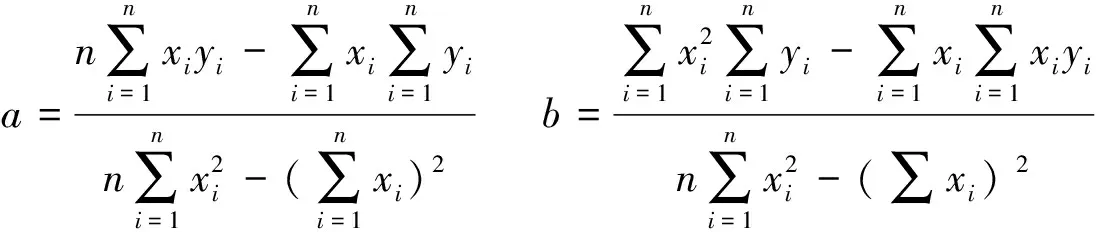
从表2可以得到：

表4 库存量表(函数关系)

经计算得：

表5 库存量表(结果值)

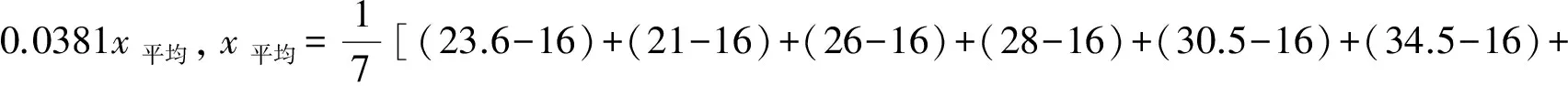
重复以上的步骤，进而可以达到预期调控的目的，上面过程很容易达成应用程序的编写，进而实施现场的控制，所以具有很高的利用价值。

[1] 张芷芬,丁同仁.微分方程定性理论[M].北京：科学出版社，1997，16-23.

[2] 马知恩.常微分方程定性与稳定性方法[M].北京：科学出版社，2001，41-59.

[3] 张锦炎,冯贝叶.常微分方程几何理论与分支问题[M].北京：北京大学出版社，2000，20-37.

[4] 刑进.浅谈企业库存管理[J].中国外资，1999(9)：61-64.

[5]YangT,YangLB,YangCM.Impulsivecontroloflorenzsystems[J].PhysD,1997,110(1):18-24.

责任编辑：程艳艳

Application of Equilibrium Point of Dynamical System in Inventory Management

LIU Yuanshu

(Academic Affairs Office, Yingkou Vocational and Technical College, Yingkou 115000, China)

Inventory management plays an important role in business administration. In order to guarantee market supply and not to produce too much inventory backlog, it is necessary for enterprises to maintain a reasonable and scientific inventory. This paper, combining the dynamical system with enterprise inventory, tries to build a mathematical model of inventory management, then adopts effective methods to adjust the enterprise inventory through analyzing the mathematical model. This model with high use value is easy to be compiled as an application program, which is implemented to control the operation.

dynamical system; safety stock; equilibrium point; regulation

2016-12-02

辽宁省职业技术教育协会科研规划课题(LZY13130)

刘元姝(1982-)，女，辽宁营口人，讲师，硕士，主要从事基础数学方面研究。

F253.4

A

1009-3907(2017)02-0016-04