多孔介质流动及传热的格子Boltzmann方法研究

吴子森，董平川*，袁忠超，周阴国，曹耐，许佳良

1 中国石油大学石油工程教育部重点实验室, 北京 102249

2 中海油研究总院开发研究院, 北京 100027

多孔介质流动及传热的格子Boltzmann方法研究

吴子森1，董平川1*，袁忠超2，周阴国1，曹耐1，许佳良1

1 中国石油大学石油工程教育部重点实验室, 北京 102249

2 中海油研究总院开发研究院, 北京 100027

基于随机四参数生长法构造不同孔隙度的多孔介质，采用稀疏矩阵存储方式存储内部流体节点、流固边界节点及物理边界节点。通过顶盖驱动流和方腔自然对流验证了格子Boltzmann方法处理多孔介质的传热问题的可行性。基于格子Boltzmann耦合传热模型，计算得到复杂多孔介质内的速度及温度分布云图，对多孔介质内的速度、温度与迭代时间及孔隙度的关系作了详细的分析。结果表明：多孔介质中速度和温度分布受孔隙度影响，相同压力梯度下，平均速度随着孔隙度的增加而增大；孔隙度相同时，平均速度随着压力梯度的增加而增大。相同温差条件下，随着孔隙度的增大，多孔介质中对流传热达到稳态的时间逐渐减小；多孔介质内最大温度出现在高温壁面处，靠近高温壁面的孔隙度越大，高温部分体积越大。相同条件下，孔隙度越小，多孔介质的平均温度越低。

四参数随机生长法；格子Boltzmann方法；多孔介质；耦合传热

0 引言

多孔介质是由固体骨架和流体组成的复合介质，多孔介质内的流动和传热过程在自然界、人类生产及生活中广泛存在[1]。从学科发展的角度看，多孔介质流动及传热问题已经渗透到许多学科和领域。地下岩层中的石油、天然气和水是自然界多孔介质中一种复杂的多元体系，研究油、气的开采、特别是石油的热采技术，促使石油工程学对多孔介质的传热传质进行系统的研究。地热资源的勘测评估和开发利用以及利用土壤岩层作为蓄热蓄冷介质，也需应用类似的理论与技术。因此对多孔介质流动及传热的研究，是一项具有重大学术价值、对学科发展和技术创新具有深远意义的研究课题[2]。

自然界中实际多孔介质形状多变而复杂，国内外许多学者对其进行了研究，主要可以归纳为“连续介质模型”和“非连续介质模型”[3]。上述模型在应用中遇到的主要问题是，由于多孔介质内部孔隙和骨架之间的边界极为复杂，有时过于简化，因此即使对模型求解也得不到有价值的信息。随着计算机技术的发展，编制程序生成满足目标孔隙度的方法也越来越多，其中Wang M.R[4]等提出的四参数随机生长法(QSGS)重构多孔介质，通过相关性比较其与实际多孔介质符合很好，QSGS方法也成重构多孔介质的主要方法。

格子Boltzmann方法是上个世纪末期发展起来的一种流体系统建模及介观尺度模拟的数值方法，与传统的计算方法相比：其主要特点是物理图像清晰、边界条件容易处理及并行性能好等[5]。因而迅速在单相流[6-7]、湍流[8]、化学反应流[9]、燃烧[10]、磁流体[11]、晶体生长[12]等领域得到了应用。

本文采用QSGS重构出不同孔隙度的多孔介质，应用稀疏矩阵存储方式将孔隙相节点、流固边界节点及物理边界节点进行存储。通过对顶盖驱动流和二维方腔自然对流的模拟分析了格子Boltzmann方法在处理流体和固相耦合传热问题可行性。基于格子Boltzmann方法，分析了复杂多孔介质内部的速度、温度与孔隙度和迭代时间的关系。

1 四参数随机生长法

Wang M R[4]等人提出的QSGS生长步骤为：①根据给定的生长核分布概率，随机播种生长核，②基于给定的生长概率Di(i表示方向)，生长核按照指定方向生长，如果相邻节点上的随机数不大于Di，则将该节点生长为骨架，③重复步骤②，直到多孔介质孔隙度等于设定的孔隙度，④输出结构数据。本文根据上述方法在计算空间中生成满足目标孔隙度的二维随机多孔介质，如图1所示：

图1 多孔介质重构图：ε=0.45(左)、ε=0.8(右)Fig. 1 Porous medium constructed by QSGS:ε=0.45(left)、ε=0.8(right)

图1中红色区域表示骨架部分，用1表示，蓝色区域表示孔隙部分，用0表示。根据以上结构图，引入函数：

式中：表示空间位置，s指红色骨架区域部分。

由以上函数可以定义孔隙度ε为：

2 格子Boltzmann方法

针对多孔介质内部流动及传热问题，本文采用双分布函数模型：即对速度和温度分别采用不同的分布函数进行描述。

2.1 速度场模型

速度场采用标准D2Q9模型，离散速度可表示为：

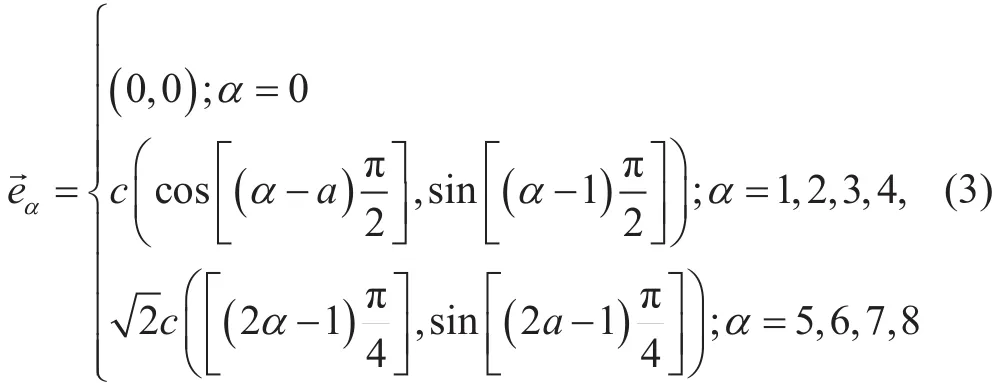
式中c表示格子速度，，Δx和Δt分别表示格子步长和时间步长，α表示9个速度方向。

无外力项的Boltzmann方程离散为如下格式：

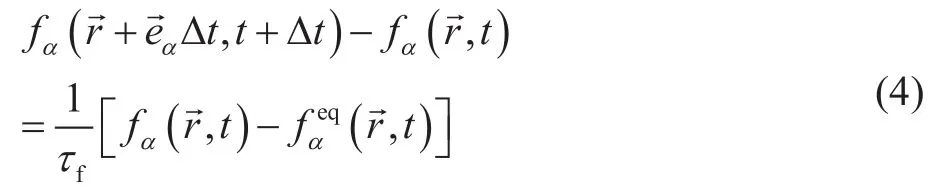
2.2 温度场模型

温度场本文仍采用D2Q9模型，温度场的分布函数演化方程描述如下：

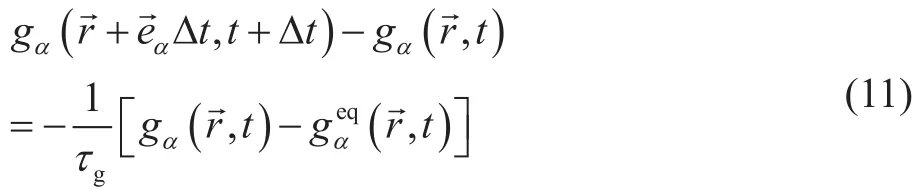
其中gα表示时刻点处温度分布函数，表示平衡态温度分布函数，τg表示弛豫时间。

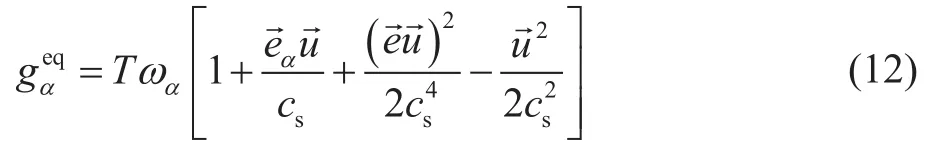
宏观温度T可根据分布函数对离度速度矢量的零阶矩求得：

通过Chapman-Enskog多尺度展开可以得到温度扩散方程：

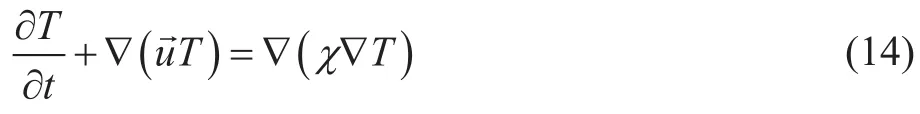
式中χ表示有效热扩散系数，方程(8)、(9)、(14)构成了完整的流动及传热数学描述。

3 问题描述

3.1 边界条件

文中模拟区域网格大小为200×200，内部是孔隙度从0.45～0.80的多孔介质，多孔介质上下边界为骨架，采用反弹格式处理，左、右边界分别为入、出口，采用压力边界条件，入口温度设为293 K，出口温度设为0 K。边界条件描述如下：

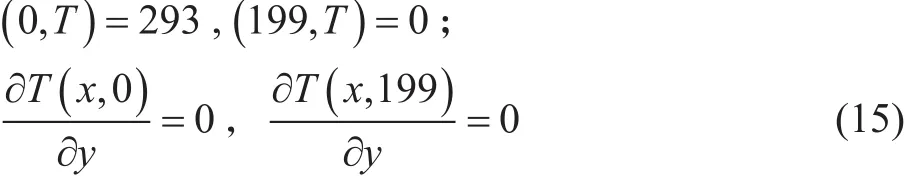
对于上述边界均采用郭照立等[13]提出的非平衡外推格式：

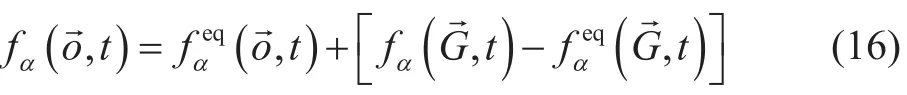
式中：为边界节点，为与边界相邻层节点。

3.2 多孔介质模型简化

一般地，流体在孔隙内的流动仍然满足N-S方程，将多孔介质的固相看作是内部流场的边界，孔隙中的流体与固相边界的相互作用通过边界条件来实现。对于多孔介质问题而言，固相部分占有很大的比重，同时固相内部没有流体流动。如果采用完全数组的数据结构，将造成内存的巨大损耗，并且也会因为对固体格点的循环操作和逻辑运算而降低计算效率。为此我们采用如图2所述的处理方法，应用一定的算法将多孔介质内部的流固边界的第一层进行识别，从而在计算的时候只需对图2中的蓝色和绿色部分进行计算，红色的部分直接初始化为0即可。这样节省了计算机的内存损耗，同时也降低了计算时间。

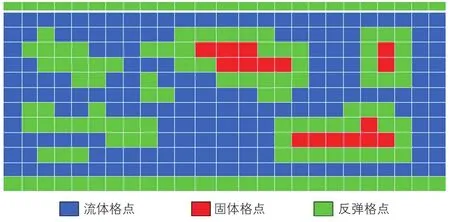
图2 多孔介质内部节点存储算法Fig. 2 Internal node storage algorithm in porous media

对于流固边界，图2中的绿色节点，采用碰撞反弹边界处理格式：f1,2,5,6=f3,4,7,8，研究表明[14]，对于低马赫数问题，其能严格的保证系统的质量和动量守恒。

4 结果与讨论

4.1 模型验证：

4.1.1 顶盖驱动流

采用顶盖驱动流的算例，验证格子Boltzmann 方法的可行性。设定Reynolds数Re=100，网格划分为65×65，松弛时间τf=0.54，初始条件设定为最顶部节点的无量纲速度u=0.1，图3为方腔内流线图，图4为截面上y方向无量纲速度分布。从图4看出LBM模拟结果与与Ghia等人[15]吻合的很好。

4.1.2 二维方腔自然对流传热

通过格子Botzmann方法模拟二维方腔自然对流，参数设定为：左侧壁面无量纲温度为20，右侧壁面无量纲温度为1，Prandtl数Pr=1，Rayleigh数Ra=103～105，网格划分为100× 100，松弛时间τf=τg=0.54。图5为流体达到稳态时流线和等温线图。

计算得到沿热壁面的平均Nu数，并与Barakos[16]等的计算结果进行对比。从表1可以看出LBM的模拟结果和Barakos的计算结果吻合度较高。本文讨论的多孔介质内的流体流动及传热问题，当流体在骨架间的孔隙内部流动时，孔隙间的骨架具有一定的温度，其传热机理及处理方法与方腔自然对流类似，因此本算例说明了LBM处理多孔介质传热问题是可行的。

图3 方腔内流函数示意图Fig. 3 Schematic diagram of fl ow function

图4x/L=0.5截面上沿Y方向无量纲速度分布Fig. 4 Non-dimensional velocity distribution along theYdirection (x/L=0.5)

4.2 结果与讨论

从图6和图7可以看出，应用格子Boltzmann方法可以得出多孔介质内部的详细流动信息：包括孔隙间的流线图、不同时间步长的温度分布云图，这是传统计算方法在处理多孔介质流动及传热问题时无法解决的难题。从图6可以看出，多孔介质内最大温度出现在高温壁面处，靠近高温壁面的孔隙率越大，高温部分体积越大。

从图8可以看出孔隙度不同，收敛时间步长不同，总体表现为孔隙度越小，收敛得越慢，原因是随着孔隙度的减小，流体的流速减慢，同时骨架份额的增多导致孔隙区域变得曲折，许多区域流体需要一定的时间才能到达。另一方面是随着孔隙度的减小，流固边界节点越来越多，需要处理的边界也越来越多，这无疑增大了计算量因此收敛的时间步长随着孔隙度的减小增大。

平均速度是整个流场速度的统计平均，在统计上消除了局部最大速度带来的偶然性。图9(a)为平均速度与孔隙度的关系曲线，从图上可以看出相同压力梯度下，平均速度随着孔隙度的增加而增大，这是由于孔隙度越大，流体的份额越多，骨架份额减少，骨架对流体流动的阻碍作用越低，使得流体的流速增加。图9(b)为平均速度与压力梯度的关系曲线，可以看出孔隙度不变时，平均速度随着压力梯度的增加而增大，这是因为压力梯度增大，驱动力变大，促进了流体的流动。

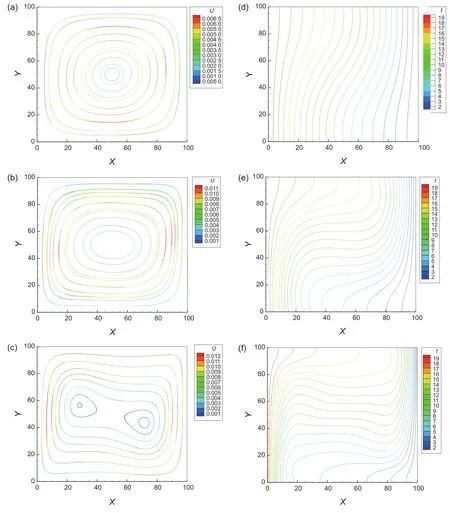
图5 不同Ra数下的流场(左)和等温线(右)Fig. 5 Streamlines (left) and isotherms (right) for differentRavalues, from top to botton,Ra= 103, 104, 105

表1 热壁面上平均Nu数与基准解的比较Table 1 Comparison of average Nusselt numbers on the hot wall between the LBM results and other published data

图6 不同时间步长的温度分布云图(ε=0.65)Fig. 6 The distribution of temperature fi eld at different time steps (ε=0.65)

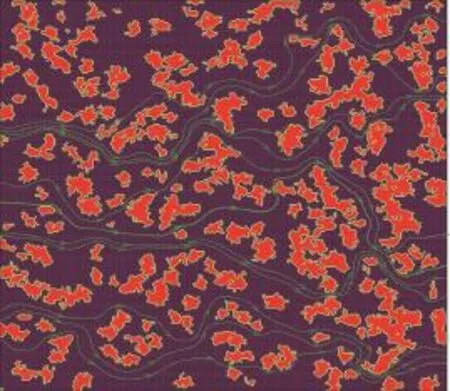
图7 多孔介质内流线图(ε=0.75)Fig. 7 The contour map of velocity (ε=0.75)

从图10、11可以看出，多孔介质进出口的速度总体呈现进口速度大于出口速度的趋势，但当ε=0.8时，呈现出口速度大于进口速度的现象，这是由于出口端固体骨架的比重小于入口端固体骨架比重。从图12可以看出，当孔隙度较小时，压降曲线在多孔介质前半部分波动较为明显，因为此时固体骨架所占比重比较大，骨架之间流道狭窄，流体流动阻力增大，导致压降变化剧烈。

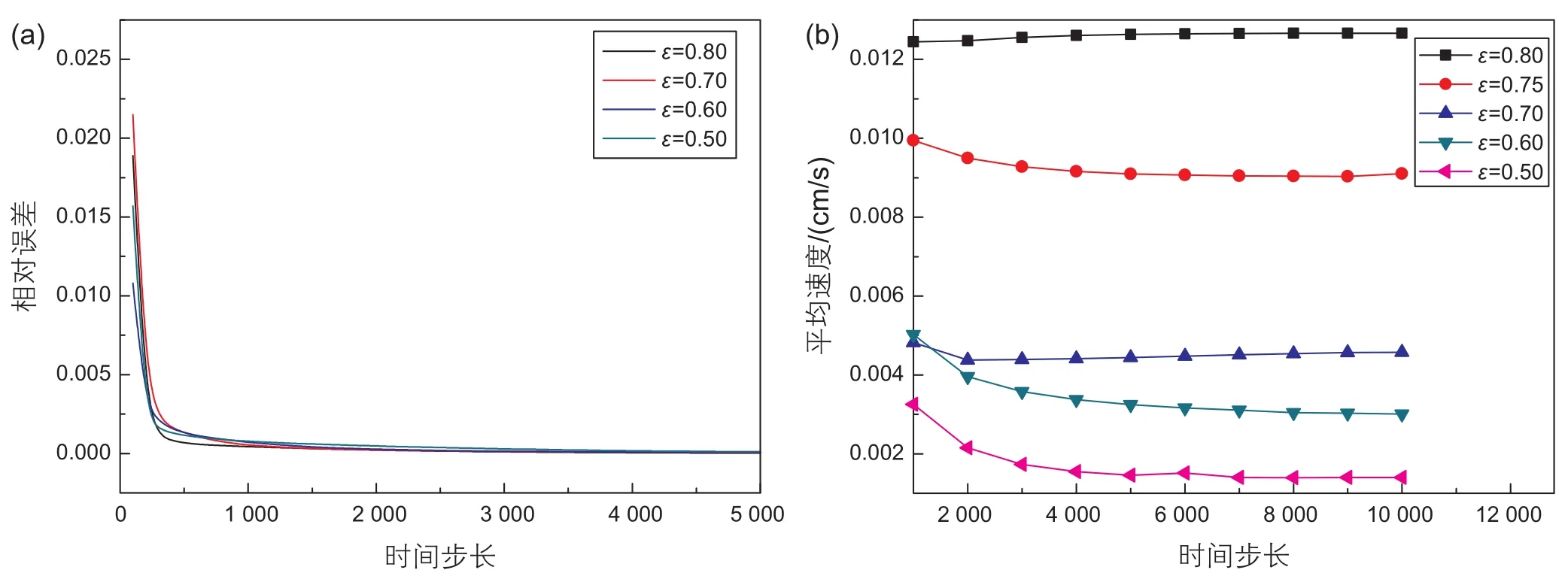
图8 不同孔隙度下最大相对误差(左)及平均速度(右)与迭代时间的关系Fig. 8 The relationship between the maximum relative error (left), average velocity (right) and iteration time with different porosity

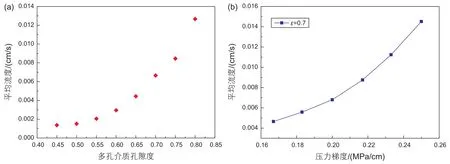
图9 平均速度与孔隙度(a)及压力梯度(b)的关系Fig. 9 The relationship between average velocity、porosity (a) and pressure gradient (b)

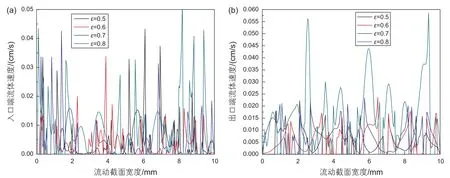
图10 不同孔隙度进出口速度：进口速度(左)、出口速度(右)Fig. 10 Velocity of inlet (left) and outlet (right) with different porosity

模拟孔隙度不同时，多孔介质平均温度随时间的变化规律。从图13可以看出孔隙度不同时，平均温度随迭代时间的变化曲线不同。在相同的迭代时间内，随着孔隙度增大，曲线斜率增大，整体的平均温度也随之升高，主要是因为随着孔隙度的增大，骨架份额较少，相应的孔隙相的比重增大，孔隙中的传热由于流体流动的存在属于强化传热，同时孔隙度越大，平均流速越大，强化传热效果得到加强，因此使得曲线斜率增大及整体的平均温度升高。

为了分析多孔介质孔隙度对温度的影响，进一步模拟了不同孔隙度下，多孔介质的温度变化。从图14中可以看出孔隙度越小，多孔介质的平均温度越低，这是因为多孔介质孔隙度越小，固相的份额越多，相应的孔隙相的份额越低，而温度由高温壁面向低温壁面传递的过程中，固相内部只有热传导，而孔隙相则既有热传导，又有热对流，使得传热程度相对较为剧烈，故而孔隙度越小的平均温度比孔隙度较大的多孔介质温度低。

图11ε=0.7时进出口速度Fig. 11 Velocity of inlet and outlet whenε=0.7

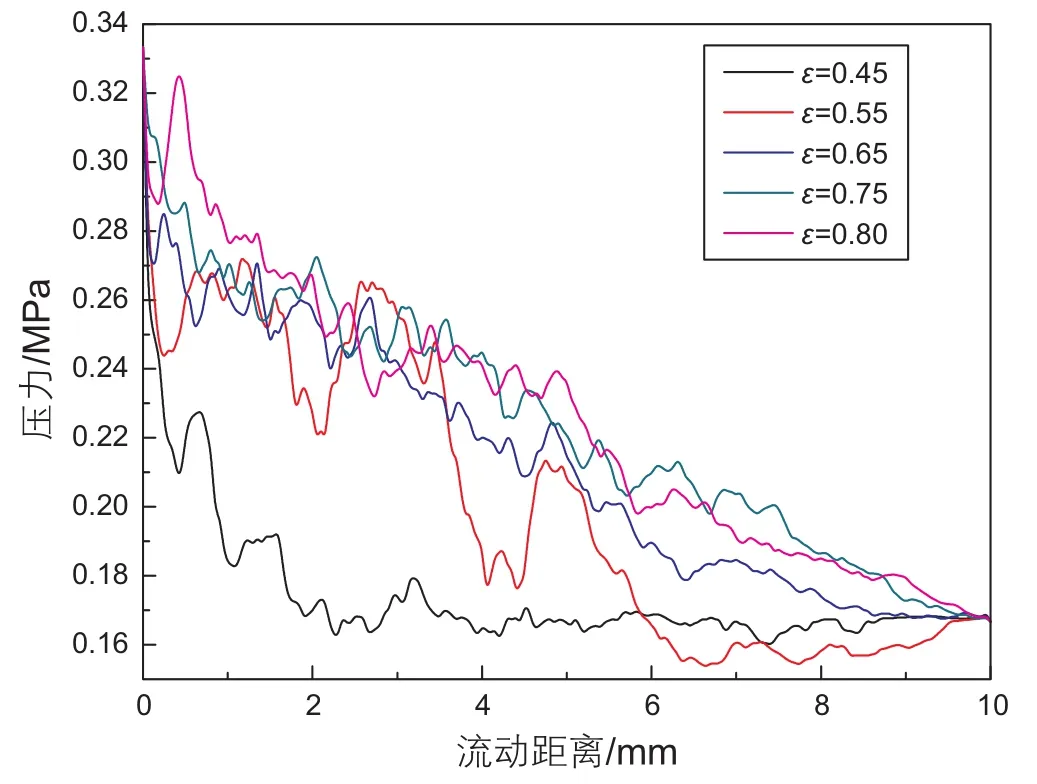
图12 不同孔隙度下的压力降落曲线Fig. 12 Pressure drop curves with different porosity

图13 孔隙度不同时平均温度与迭代时间步长的关系Fig. 13 The relationship between average temperature and iteration time step with different porosity

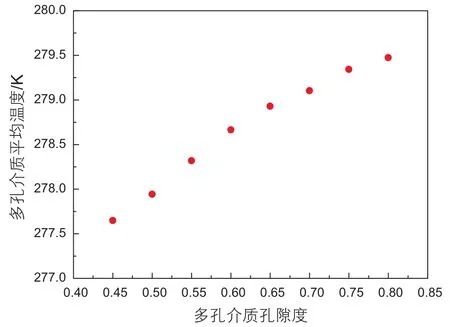
图14 平均温度与孔隙度的关系Fig. 14 Relationship between average temperature and porosity

5 结论

基于格子Boltzmann方法耦合传热模型，计算得到复杂多孔介质内的速度及温度分布云图，对多孔介质内的速度、温度与迭代时间及孔隙度的关系作了详细的分析。结果表明：流体的速度场和温度场受多孔介质孔隙度影响。相同压力梯度下，平均速度随着孔隙度的增加而增大；孔隙度相同时，平均速度随着压力梯度的增加而增大。相同温差条件下，随着孔隙度的增大，多孔介质中对流传热达到稳态的时间逐渐减小；多孔介质内最大温度出现在高温壁面处，靠近高温壁面的孔隙度越大，高温部分体积越大。相同条件下，孔隙度越小，多孔介质的平均温度越低。格子Boltzmann方法能处理多孔介质的流动及传热问题，并能得出相关物理量随孔隙度的变化关系，可以为处理更为复杂的多孔介质传热及流动问题提供理论指导。

[1] DULLIEN F. Porous media fl uid transport and pore structure[M]. Utah: Academic Press, 1992.

[2] 姚军, 孙致学, 张凯, 等. 非常规油气藏开采中的工程科学问题及其发展趋势[J]. 石油科学通报, 2016, 1(1): 128-142. [YAO J, SUN Z X, ZHANG K, et al. Scienti fi c engineering problems and development trends in unconventional oil and gas reservoirs[J]. Petroleum Science Bulletin, 2016, 1(1): 128-142.]

[3] BEAR J. Dynamics of fl uids in porous media[M]. New York: Dover Publications, 1989.

[4] WANG M, WANG J, PAN N, et al. Mesoscopic predictions of the effective thermal conductivity for microscale random porous media[J]. Physical Review E, 2007, 75(2): 036 702-036 711.

[5] 何雅玲, 王勇, 李庆. 格子 Boltzmann 方法的理论及应用[M]. 北京:科学出版社, 2009.[HE Y L, WANG Y, LI Q. Lattice Boltzmann Method: Theory and application[M]. Beijing: Science Press, 2009. ]

[6] 张磊, 姚军, 孙海, 等. 基于数字岩心技术的气体解析/扩散格子Boltzmann模拟[J]. 石油学报, 2015, 36(3): 361-365.[ZHANG L, YAO J, SUN H, et al. Lattice Boltzmann simulation of gas desorption and diffusion based on digital core technology[J]. Acta Petrolei Sinica, 2015, 36(3): 361-365.]

[7] 张磊, 康钦军, 姚军, 等. 页岩压裂中压裂液返排率低的孔隙尺度模拟与解释[J]. 科学通报, 2014, 59(32): 3197-3203.[ZHANG L, KANG Q J, YAO J, et al. The explanation of low recovery of fracturing fl uid in shale hydraulic fracturing by pore-scale simulation[J]. Chinese Science Bulletin, 2014, 59(32): 3197-3203.]

[8] CHEN H, SATHEESH K, STEVEN O, et al. Extended Boltzmann kinetic equation for turbulent fl ows[J]. Science, 2003, 301(5633): 633-636.

[9] CHEN S Y, DAWSON S P, DOOLEN G D, et al. Lattice Method and their applications to reaction systems[J]. Computers & Chemical Engineering, 1995, 19(4):395-408.

[10] YU H D, LUO L S, GIRIMAJI S. Scalar mixing and chemical reaction simulations using Lattice Boltzmann Method[J]. International Journal of Computational Engineering Science, 2012, 3(1):73-87.

[11] CHEN S, CHEN H, MARTNEZ D, et al. Lattice Boltzmann model for simulation of magnetohydro dynamics[J]. Physical Review Letters, 1991, 67(27): 3776-3779.

[12] MILLER W, SUCCI S, MANSUTTI D. Lattice Boltzmann model for anisotropic liquid-solid phase transition[J]. Physical Revive Letters, 2001, 86(16): 3578-3581.

[13] 郭照立,郑楚光. 格子Boltzmann方法的原理及应用[M].北京: 科学出版社, 2009.[GUO Z L, ZHENG C G. Theory and applications of Lattice Boltzmann Method[M]. Beijing: Science Press, 2009.]

[14] ZIEGLER D P. Boundary conditions for Lattice Boltzmann simulations[J]. Journal of Statistical Physics, 1993, 71(5): 1171-1177.

[15] GHIA U, GHIA K N, SHIN C T. High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method[J]. Journal of Computational Physics, 1982, 48(3): 387-411.

[16] BARAKOS G, MITSOULIS E, ASSIMACOPOULOS D. Natural convection fl ow in a square cavity revisited: Laminar and turbulent models with wall functions[J]. International Journal for Numerical Methods in Fluids, 1994, 18(7): 695-719.

Study of flow and heat transfer in porous media based on the Lattice Boltzmann Method

WU Zisen1, DONG Pingchuan1, YUAN Zhongchao2, ZHOU Yinguo1, CAO Nai1, XU Jialiang1
1 MOE Key Laboratory of Petroleum Engineering, China University of Petroleum-Beijing, Beijing 102249, China
2 CNOOC Research Institute, Beijing 100027, China

A porous medium with different porosity is modelled based on the random four parameters growth method and the Sparse Matrix Storage Formats is used to store the internal fl uid node, the fl uid solid boundary node and the physical boundary node. The simulation of lid driven fl ow and natural convection in a square cavity are studied and the correctness of the Lattice Boltzmann model is verified. Based on the lattice Boltzmann method, the velocity and temperature field distribution in the complex porous medium are calculated, and the relationship between velocity or temperature and each of iteration time and porosity are analyzed in detail respectively. The results show that the distributions of fl uid velocity and temperature are affected by the porosity of the porous medium. With an increase of porosity, the average velocity increases under the same pressure gradient; with an increase of pressure gradient, the average velocity increases under the same porosity. At the same temperature, with the increase of porosity, the time convection heat transfer reaches a steady-state in the porous medium is gradually reduced. The maximum temperature appears at the high temperature surface, and the bigger the porosity near the high temperature wall, the greater the volume of the high temperature part. With a decrease of porosity, the average temperature of the porous medium decreases under the same condition.

quartet structure generation method; Lattice Boltzmann Method; porous media; coupled heat transfer

10.3969/j.issn.2096-1693.2017.01.008

(编辑 马桂霞)

*通信作者, dpcofm@163.com

2016-07-09

吴子森, 董平川, 袁忠超, 周阴国, 曹耐, 许佳良. 多孔介质流动及传热的格子Boltzmann方法研究. 石油科学通报, 2017, 01: 76-85

WU Zisen, DONG Pingchuan, YUAN Zhongchao, ZHOU Yinguo, CAO Nai, XU Jialiang. Study of fl ow and heat transfer in porous media based on the Lattice Boltzmann Method. Petroleum Science Bulletin, 2017, 01: 76-85. doi: 10.3969/j.issn.2096-1693.2017.01.008